认知无线电网络中基于博弈论的频谱切换方法*

彭云飞，邵 尉，卢春兰

（陆军工程大学，江苏 南京 210007）

0 引言

随着5G 和物联网（Internet of Things，IoT）技术的快速发展和无线设备数量的爆炸式增长，频谱使用需求日益增长，频谱资源日趋紧张。

认知无线电网络[1]（Cognitive Radio Networks，CRN）允许次用户（Secondary User，SU）对许可频谱进行机会性使用。当主用户（Primary User，PU）到达时，SU 无论是切换至另一信道还是保持在当前信道，都将面临潜在的频谱占用冲突。一些研究工作将博弈论与认知无线电网络相结合。例如，文献[1]将空闲频谱进行定价，并将PU 之间的价格竞争定义为博弈。文献[2]研究了一种基于博弈论和拍卖理论的认知无线电车载网络频谱切换优化方案，以及一种基于成本函数的多属性决策方法，用于最优信道选择。文献[3]提出了一套基于欺骗的防御策略，以保护CRN 免受欺骗性攻击。认知干扰器和认知用户的相互作用被建模为Stackelberg 博弈。在已有的各种频谱切换方法中，优化目标都不尽相同；文献[4]的优化目标是最小化信道接入时间；提高频谱切换效率也是优化目标之一[5]；或者想提升系统总的吞吐量[6]。

在CRN 中，SU 必须竞争使用有限的频谱资源，机会式地利用频谱的SU之间是存在干扰的的特性。当累积干扰超过一定的阈值时，会对网络的服务质量（Quality of Service，QoS）产生影响。而博弈论是解决竞争优化问题的方法之一，因此本文将博弈论运用于CRN 的频谱切换问题。当PU 到达时，无论SU 选择切换或等待，都将面临潜在的频谱占用冲突。因此，定义新的期望累积切换时延，将频谱切换问题表征为Stochastic 博弈，并利用空间自适应博弈（Spatial Adaptive Play，SAP）算法找到问题的最优解。

1 系统模型和问题表述

1.1 系统模型

在如图1 所示的一个有N个SU 和M个信道的分布式CRN 中，N>M。许可信道归PU 所有。当不被PU 占用时，SU 可以机会使用它们。由于不存在中心节点，SU 自主选择切换时接入的信道。

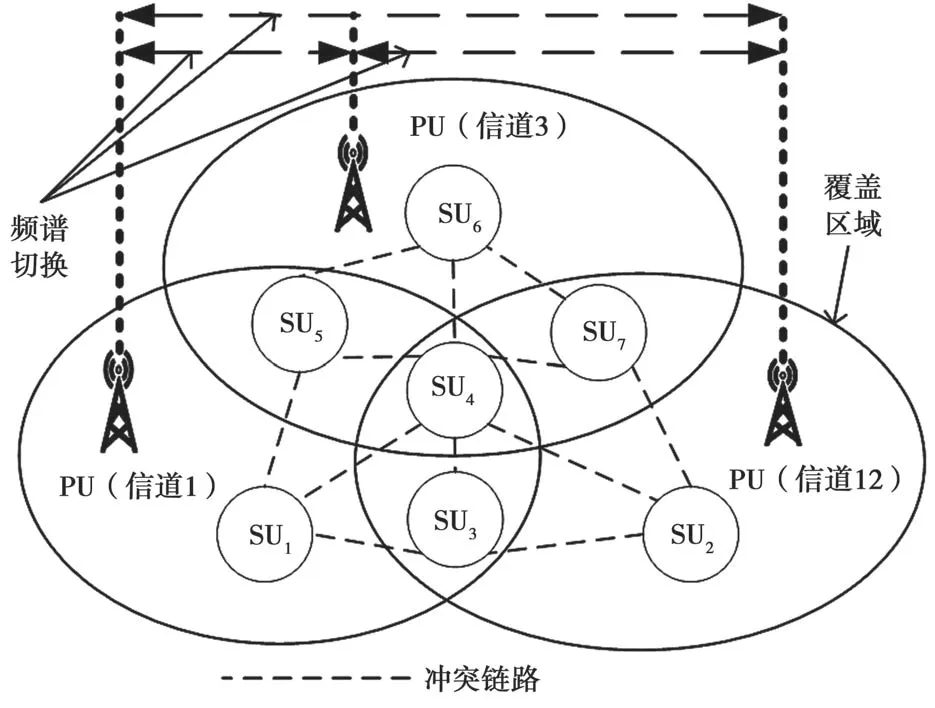
图1 CRN 中的频谱切换场景

利用抢先恢复优先级（Preemptive Resume Priority，PRP）M/G/1 排队网络模型[7]来描述不同信道中具有多次频谱切换的PU 和SU 之间的频谱使用行为。假设每个信道的队列中PU 和SU 的到达过程均服从泊松分布。图2 为SU1传输的切换过程。Ts为频谱切换时延，T为SU1的整个数据传输时间。

图2 活跃SU1 传输的切换过程

传输过程被中断3 次，整个传输过程被分为4个部分。

该过程可描述如下。

（1）起初，SU1在初始信道1 上传输。当PU到达时，SU1根据切换时延最短的原则决定其目标信道。

（2）在第1 次中断时，因为切换至信道2 的切换时延最短，SU1切换至空闲信道2 继续传输。

（3）第2 次中断时，因为停留在信道2 的切换时延最短，SU1选择等待，待PU 传输完成后继续传输。此时，Twait是信道2 被PU 占用的持续时间，也是SU1的等待时间。

（4）在第3 次中断时，虽然此时信道3 处于忙的状态，但与SU1一起排队等待服务的SU 少，即切换至信道3 的切换时延最短，等待当前PU或队列之前的SU 均被服务后，SU1切换至信道3继续传输。

（5）最后，SU1在信道3 上完成传输。

1.2 问题表述

SUi在传输过程中可能会多次中断，设B为中断次数，bmax表示最大中断次数，当B>bmax时，SUi整个过程传输失败，需要重新传输，则累积切换时延为：

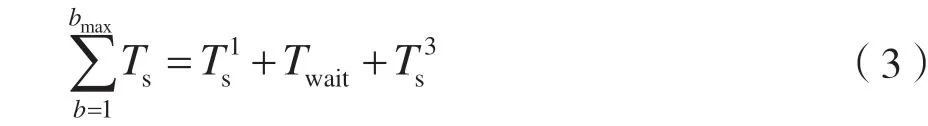
定义期望累积切换时延为：

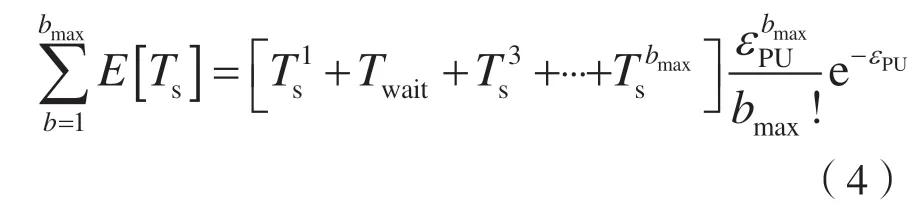
本文中以最小化SUi的期望累积切换时延（Expected Cumulative Handover Delay，ECHD）为优化目标，可表述为优化问题P：

优化问题P是一个组合问题，也是一个典型的NP-hard 问题。考虑到信道条件是动态的实际情况，求解P变得更具挑战性。

2 博弈模型和学习算法

由于考虑的CRN 中没有设定基站，因此SU 将自适应地采用频谱切换策略，可将切换问题公式化为一个Stochastic 博弈。下文提出了公式化的博弈模型，分析其性质并利用SAP 算法，以在动态环境中找到问题的最优解。

2.1 频谱切换博弈

将SU 之间的相互作用建模为一个分布式频谱切换Stochastic 博弈，表示为：

式中：N 为SU 集；Ai 为SUi的可用信道集；Ui是SUi的效用函数。

将效用函数Ui定义为ECHD 的相反数：

在Stochastic 博弈中，每个SU 都希望最大化自身的效用函数，意味着局部合作的频谱切换博弈可以表示为：

从文献[8]中可以得出结论：每一个有限的策略博弈至少存在一个混合策略NE 点。在博弈模型G中，可用信道数是有限的，所以G至少存在一个NE 点，即频谱切换问题的最优解。

2.2 学习算法

一般来说，SAP 是基于博弈论的方法中的代表性学习算法之一[9]，可以达到最佳的Nash 均衡状态，同时也适用于动态网络。考虑到认知无线电网络的动态特性，本文采用SAP 算法找到问题的最优解。

3 仿真分析

下面设计仿真实验并对结果进行分析。

首先，设定N=15、M=3，在不同的学习步长参数条件下，对比所提方案的期望累积切换时延性能，结果如图3 和图4 所示。分别在4 种学习步长条件下开展仿真比较，找出合理的学习步长设定。由图3 和图4 可得出结论，学习步长等于迭代数是相对理想的学习步长设定。

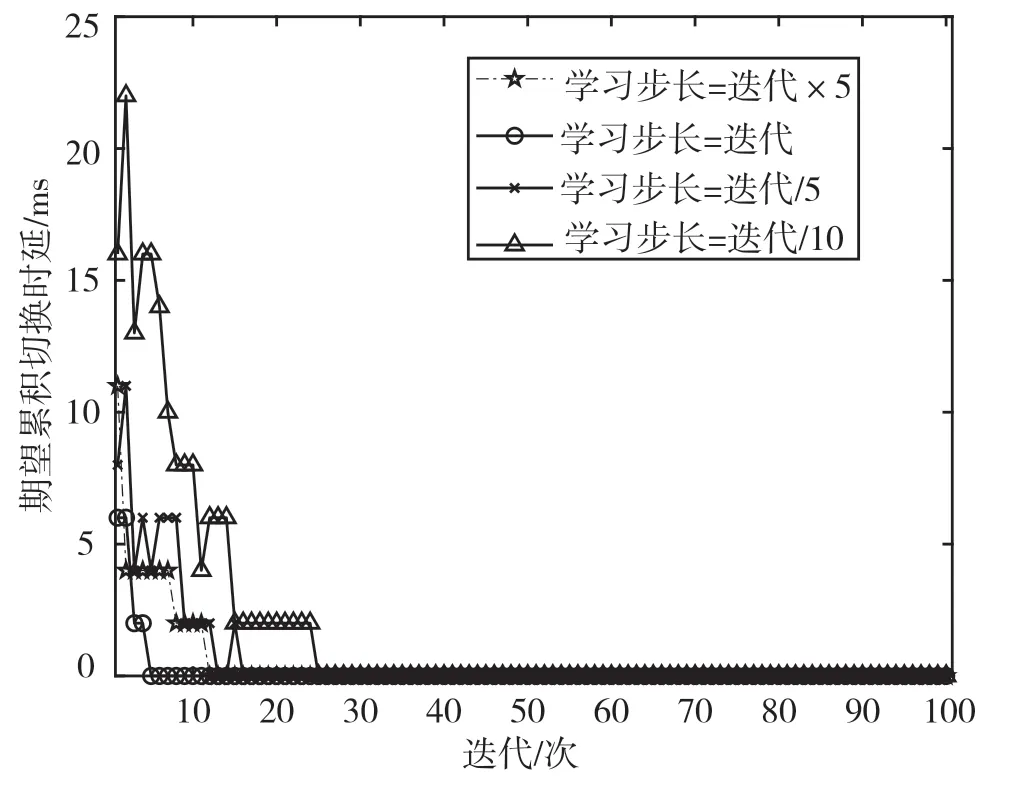
图3 不同学习步长条件下所提方案的期望累积切换时延对比

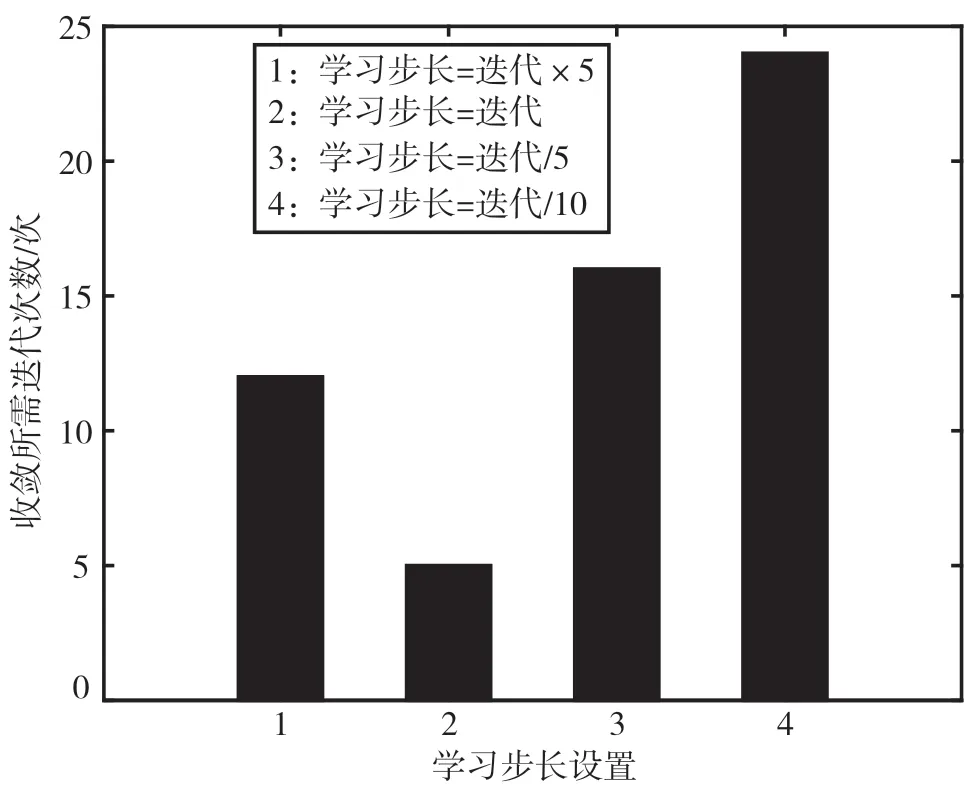
图4 不同学习步长条件下收敛所需迭代次数对比

其次，在学习步长等于迭代数的条件下，固定N=15，并在可用信道数分别为2、3、4 的情况下将所提方案与最佳响应动态（Best Response Dynamics，BRD）算法[10]进行对比，结果如图5、图6 和图7 所示。

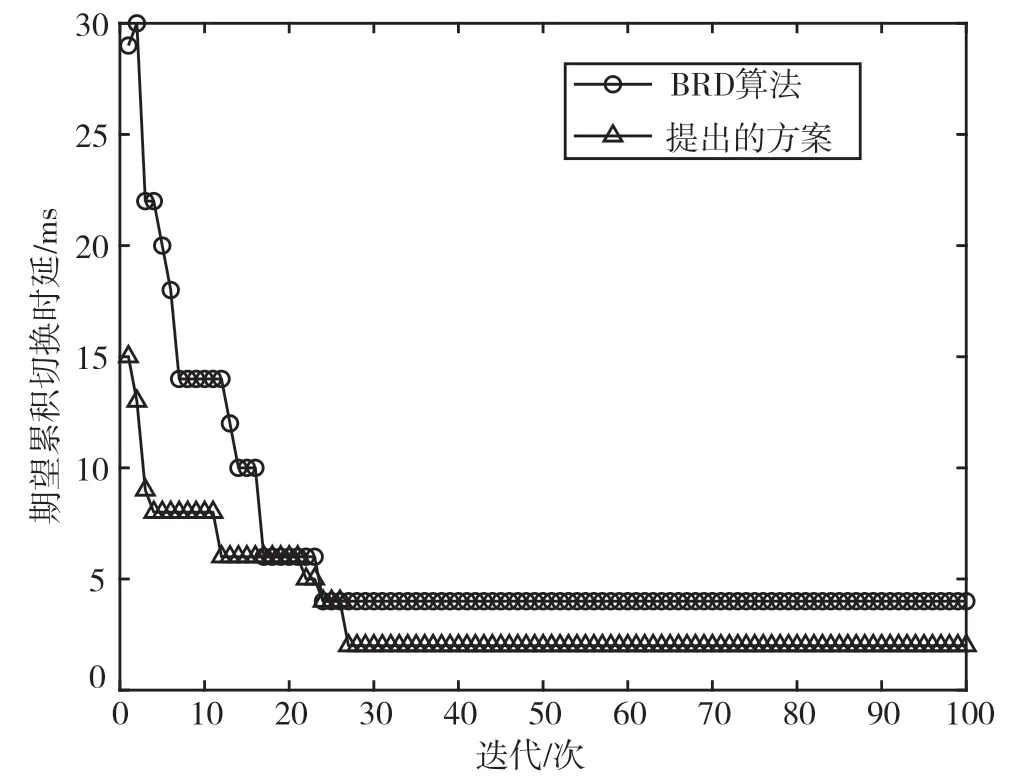
图5 M=2 时两种算法收敛性能比较

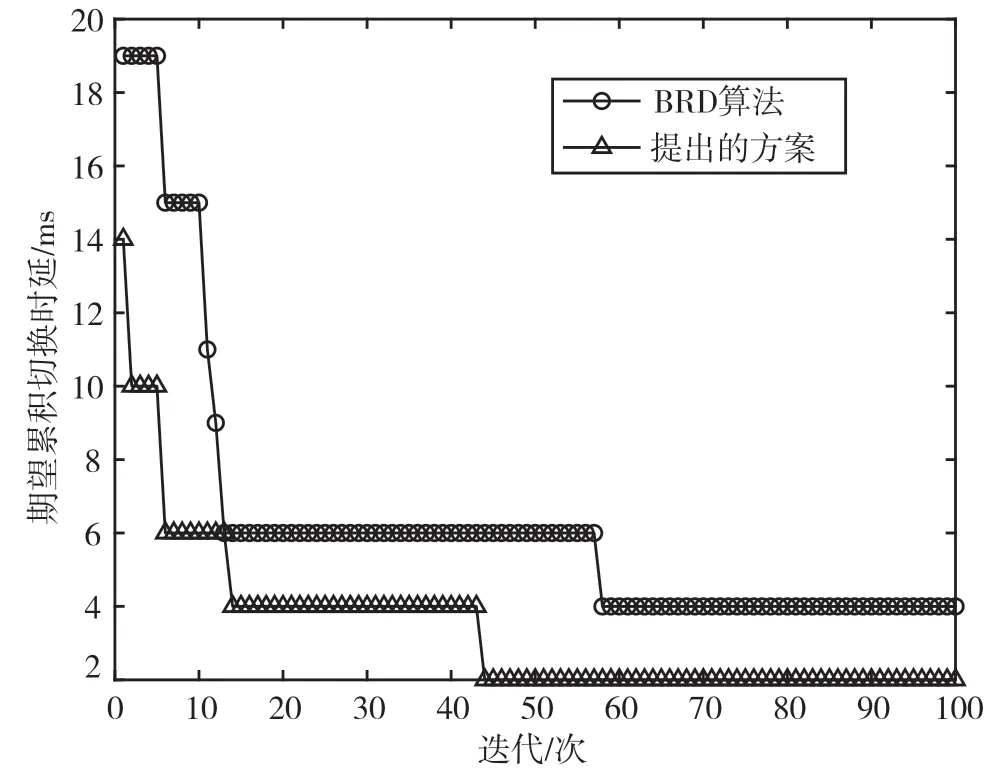
图6 M=3 时两种算法收敛性能比较

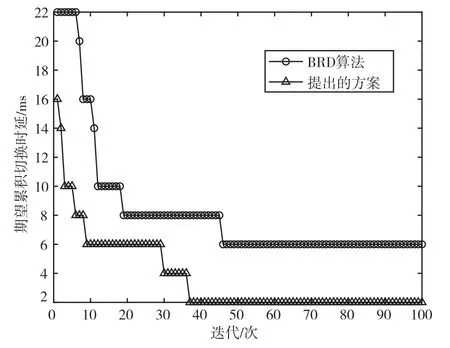
图7 M=4 时两种算法收敛性能比较

从图5、图6 和图7 可以看出，所提的方案在收敛速度和期望累积切换时延方面始终优于BRD算法，且可用信道数越多。所提方案与BRD 算法的ECHD 的差距越大，说明所提方案在多策略的情况下找到的问题可行解比BRD 算法更优，即适用于更大规模的CRN。

4 结语

本文研究了CRN 中基于博弈论的频谱切换方法，将该频谱切换问题表征为一个Stochastic 博弈，分析其性质，并利用SAP 算法来实现NE 点，找到问题的最优解。仿真结果表明，所提方案在收敛速度和期望累积切换时延方面方面的性能优于BRD算法，有助于提高CRN 的频谱利用效率和优化频谱切换时延。