基于近端策略优化算法的频谱切换问题研究*

李淑丰，邵 尉，谢 然，于玉江

（1.陆军工程大学，江苏 南京 210000；2.31107 部队，江苏 南京 210000；3.江苏省生态环境监控中心，江苏 南京 210002）

0 引言

认知无线电（Cognitive Radio，CR）技术作为应对频谱资源短缺问题的有效手段，近年来备受关注。认知用户/次用户（Secondary User，SU）机会式地接入提前划分给授权用户/主用户（Primary User，PU）的空闲信道。为了不对主用户造成影响，当主用户返回信道时，次用户必须立刻中断传输让出信道。因此，频谱切换技术在认知无线网络（Cognitive Radio Network，CRN）中必不可少。频谱切换的目的是将次用户对主用户产生的影响最小化，同时通过适时和智能化的频谱切换，可以将次用户自身因中断受到的影响降到最低，最大程度上保证次用户的性能要求。

频谱切换问题一般可以转换成顺序决策问题，从而建模成马尔科夫决策过程（Markove Decision Process，MDP），通过优化方法得到最优解。强化学习（Reinforcement Learning，RL）可以提供一种稳健的方法，在不确定的动态环境下处理MDP问题，而难以优化的目标也可以在RL 框架中通过设计与最终目标相关的奖励得到很好的解决[1-2]。强化学习分为两类不同的算法：基于价值函数的最优价值（Optimal Value，OV）算法和基于策略的策略梯度（Policy Gradient，PG）算法。OV 算法在学习过程中不断更新值函数，策略的评估和改进都需要依赖值函数。常用的最优价值算法包括基于模型的动态规划方法、无模型的蒙特卡洛方法和时间差分方法（如SARSA、Q-Learning 算法）。PG 算法直接基于长期回报期望进行优化，使用的是基于梯度的优化方法，在学习策略模型过程中表现更稳定。常用的策略梯度算法包括REINFORCE 方法和演员-评论家（Actor-Critic，AC）类方法。

强化学习已经被广泛应用在CRN 中[3-5]，但关于频谱切换问题的相关研究不多[6-9]。文献[6]基于Q-Learning 算法提出了用户体验质量（Quality-of-Experience，QoE）驱动的频谱切换方案。该方案使用发送比特率、帧速率和总误包率的平均意见分作为Q-Learning 的奖励函数，通过长期奖励的最大化来提高用户的满意度。文献[7]提出了一种基于实测丢包率的Q-Learning 频谱切换方案。仿真结果表明，与基于计算丢包率的方案相比，该方案在动态环境下收敛速度更快。文献[8]提出基于Q-Learning算法的智能频谱切换方法，以最大化用户QoE。与基于数据库的最优选择策略相比，该方法在经过长期训练的条件下能够达到最优QoE，可以显著减少切换次数。文献[9]将RL 模型应用于多信道多节点无线网格网络中的频谱切换，并使用学徒学习以缩短新加入节点做出正确频谱切换决策的时间。

可以看到，大部分将强化学习算法应用于频谱切换的文献中使用的都是最优价值算法，而对于策略梯度算法的应用鲜有研究。本文首次将基于策略梯度的近端策略优化（Proximal Policy Optimization，PPO）算法用于解决频谱切换问题。该方法相较于基于最优价值算法的频谱切换方案具有更好的收敛性和稳定性，能够为次用户带来更高的可用数据速率，从而提高系统的整体效益。

1 策略梯度算法模型

在行为空间规模庞大或者是连续行为的情况下，基于值函数的强化学习很难学习到一个好的结果。这种情况下可以直接进行策略学习，即将策略看成是状态和行为的带参数的策略函数或策略网络（Policy Network）a=π(a|s;θ)（简写为πθ），通过建立恰当的目标函数，利用个体与环境进行交互产生的奖励学习得到并优化策略函数的参数。

1.1 策略梯度

策略函数πθ确定了在给定的状态和一定的参数设置下采取任何可能行为的概率，是一个概率密度函数。在实际应用这个策略时，选择最大概率对应的行为或者以此为基础进行一定程度的采样探索。可以认为，参数θ决定了策略的具体形式。因而求解基于策略的学习问题转变为如何确定策略函数的参数θ。同样，可以设计一个基于参数θ的目标函数J(θ)，通过相应的算法来寻找最优参数使目标函数最大化，即。求解此最大化问题可以用梯度上升更新θ，使得J(θ)不断增大。设当前策略网络的参数为θnow，做梯度上升更新参数，得到新的参数：

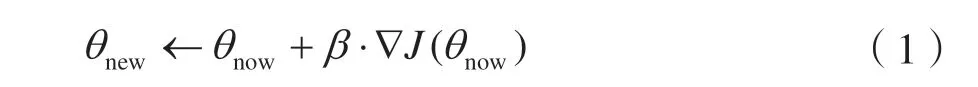
式中：β为学习率；∇J(θnow)为策略梯度。

如果用τ=(s0,a0,…,st,at)表示使用策略πθ与环境进行交互得到的一条轨迹，r(τ)表示该轨迹的总体回报，则J(θ)可以用轨迹的期望回报表示：

则策略梯度 ∇J(θ)[10]为：

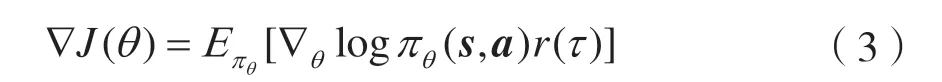
用轨迹的回报表示整个序列的价值，优点是准确无偏。但是，真实训练过程中，不充足的交互得到的轨迹数据会带来较大的方差。为了模型的稳定，可以牺牲一定的偏差来换取方差变小。其中，一种方法就是采用Actor-Critic 算法，用一个独立的模型估计轨迹的长期回报，而不再直接使用轨迹的真实回报。

1.2 Actor-Critic 算法

算法整体包含了两个网络：一个是策略网络（Actor Network），用πθ(s,a)表示；一个是价值网络（Critic Network），用Qω(s,a)表示。其中，下标θ、ω分别表示两个网络中可训练的参数。策略网络相当于演员，基于状态s做出动作a。价值网络相当于评委，给演员的表现打分，量化在状态s做出动作a的好坏程度。

对于策略网络的训练，仍使用策略梯度 ∇J(θ)来更新参数θ，不同的是需要将回报r(τ)更换为价值函数：

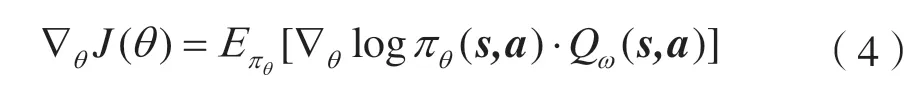
对于价值网络，使用SARSA 算法更新。定义它的损失函数为：

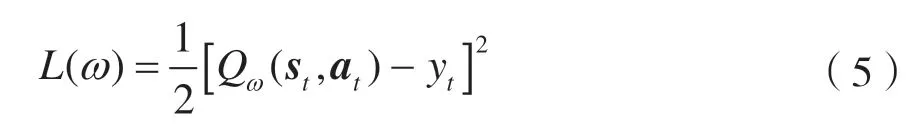
式中：yt为时序差分（Temporal Difference）目标。

则损失函数L(ω)的梯度为：

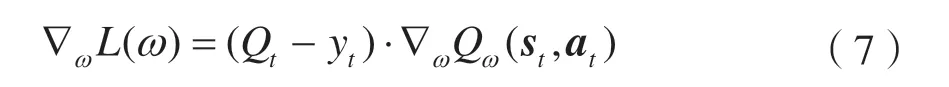
如果将式（4）中的Qω(s,a)更换为优势函数（Advantage Function），即：

可得到AC 的优化算法——（Advantage Actor-Critic，A2C）。进一步采用多线程并行的交互采样和训练，可以得到Asynchronous Advantage Actor-Critic，即A3C。

1.3 PPO 算法

AC 算法（包括A2C、A3C 算法）在一定程度上减小了模型的波动性，但未能达到很好的效果。此外，AC 属于on-policy 策略，每更新一次参数都需要进行重新的采样，导致参数更新慢。PPO 方法则对以上两个方面进行了改善，具有两个优势：一是利用替代函数理论解决训练步长问题，确保策略模型在优化时单调提升，从而使模型表现更稳定，收敛曲线不会剧烈波动；二是通过重要性采样（Importance Sampling，IS）将on-policy 策略转化为off-policy 策略，用更少的经验达到与策略梯度方法相同的表现。

PPO 算法简化自置信区域策略优化（Trust Region Policy Optimization，TRPO）算法。TRPO 算法的核心思想是在一定的置信域区间上对复杂函数做近似，再求解近似函数的最大化。PG 算法存在的核心问题是数据偏差，如果策略一次更新太远，那么下一次采样将完全偏离，导致策略更新到完全偏离的位置，从而形成恶性循环。因此，TRPO 的核心思想是让每一次的策略更新在一个置信区域内，保证policy 的单调提升。

TRPO 算法的问题定义[11]如下：

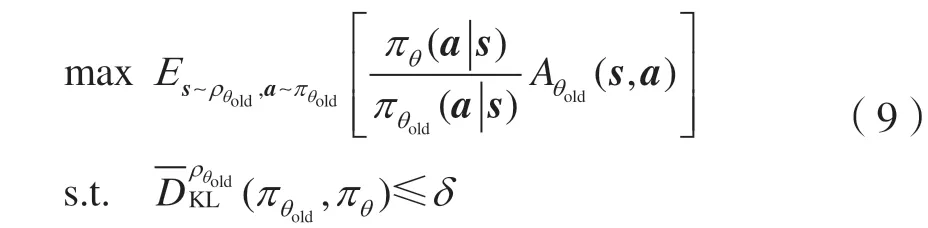
式中：πθ(a|s)为策略训练过程中不断更新的新策略；πθold(a|s)为与环境交互的旧策略，在一定批次的更新后，新策略的参数θ将更新至旧策略；Aθold(s|a)为价值网络输出的优势函数。式（9）第二行为约束条件，要求新的策略概率不能与旧策略概率分布差距太大，以保证优化的稳定性。

PPO 算法简化了TRPO 算法，基本思想是将约束条件转化为简单的新旧策略的比值约束，提出了一种新的目标函数[12]：

相当于IS 中的重要性权重（Importance Weight）。式（12）中的clip(·)为锁值函数，将新旧策略概率的比率rt(θ)取值限制在[1-ε,1+ε]，确保每一次的更新不会有太大波动。min(·)函数的作用是在两个值中选择一个较低值作为结果。

2 基于PPO 的频谱切换方案设计

本文考虑异构认知无线网络中的频谱切换问题，其中次用户机会式地接入被主用户预先占用的信道。为了满足次用户的需求，使用PPO 算法设计了一种新的频谱切换方案。该方案能最大限度地提高认知无线网络的吞吐量，提高了频谱切换的效率和可靠性。

2.1 系统模型

图1 为考虑由不同标准的网络如LTE、Wi-Fi和5G 网络组成的异构认知无线网络环境。不同网络的可用比特率（Available Bit Rate，ABR）不同。每个网络有几个独立的信道，每个信道存在授权的主用户。次用户可以访问这些信道中的任何一个，但必须保证不对主用户产生干扰，因此次用户必须定期执行频谱检测，以监视主用户的到达并确定新的可用信道。本文假设通过宽带频谱感知技术[13]，次用户可以了解所有信道的占用状态，但是无法得知主用户的流量模型。主用户和次用户对信道的占用是时隙的（Time Slotted）。

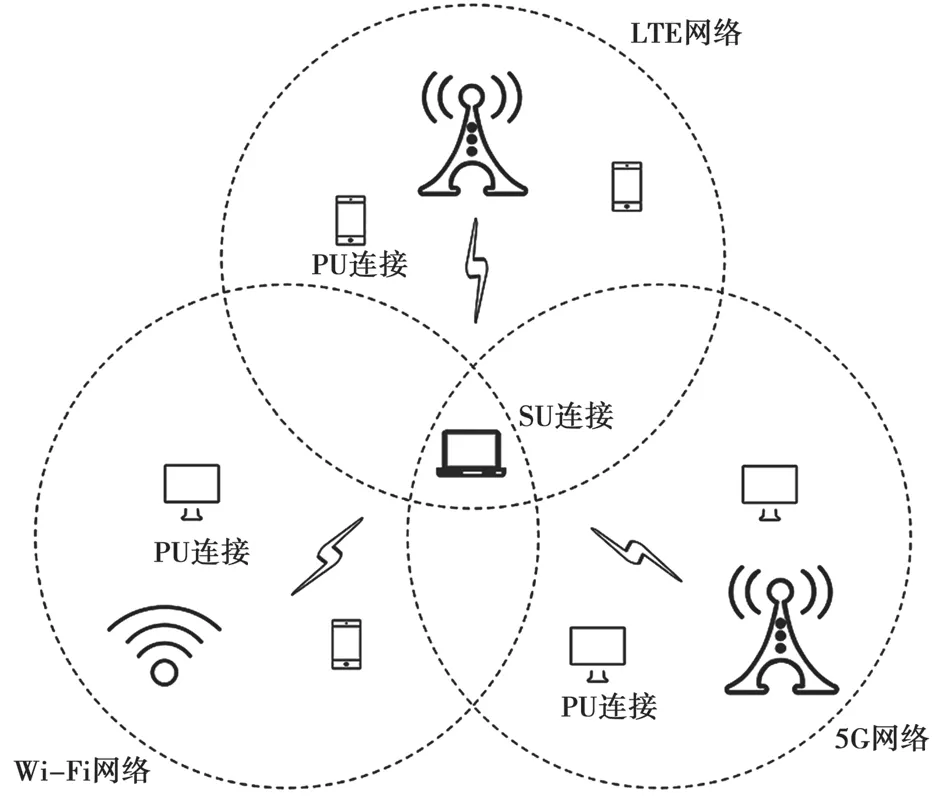
图1 异构认知无线网络环境模型

假设主用户的到达过程服从泊松分布，将主用户在通道i中的到达率表示为，相应的服务时间表示为。当次用户在一个信道中传输时，它将被返回信道的主用户所中断。此时切换程序启动，次用户执行频谱感知来检测一个可用的信道作为目标信道并切换[14]。如果多个信道被检测为空闲信道，则通过切换算法确定目标信道。另外，如果所有信道都非空闲或者切换算法确定留在当前信道更有利，次用户将留在队列中，在主用户离开后继续未完成的传输而不是执行切换。

将基于PPO 方法的频谱切换问题建模成MDP问题，其中次用户作为一个智能体（Agent）行动，在时隙t感知环境并得到观测状态s。在状态s下，次用户依据策略π选择动作a。基于动作a，状态s依照转移概率转移至状态s_，并得到回报。上述过程的一次实际实现结果被称为一条经验（Experience），可以用元组(s,a,r,s_)表示。基于多条经验值，PPO 分别更新策略网络和价值网络。重复上述过程直至策略收敛。

状态空间：将次用户在时隙t时的状态表示为st=[Φt,at-1,dt]T，其中表示许可信道k的空闲或被占用状态。at-1表示次用户在前一时隙中采取的动作，即从时隙t-1 开始，次用户在信道at-1中传输，直至主用户在时隙t时返回。dt 为次用户到时隙t为止的累积等待时间，即多次切换而导致的累积延迟。

动作空间：将次用户在时隙t时的动作表示为at∈(c1,c2,…,ck)，其中ci表示授权信道i。在时隙t发生碰撞时，次用户从k个信道中选择一个进行下面的传输。如果at=at-1，则表示次用户将停留在当前信道，否则将切换到另一个信道。

回报函数：本文考虑对网络状况较为敏感的具有延时约束的应用数据，如视频流数据。在此基础上，提出了一种新的基于QoE 的回报函数：

式中：Q(PSNR)为峰值信噪比（Peak Signal-to-Noise Ratio，PSNR）的函数[15]。

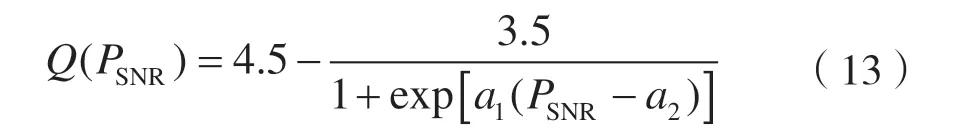
式中：a1和a2是决定函数形状的参数；PSNR为经验峰值信噪比[16]，可以表示为：

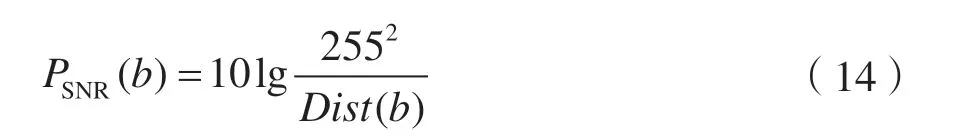
式（14）是一个关于网络可用比特率b的凹效用函数，式中编码器失真项Dist(b)可表示为：

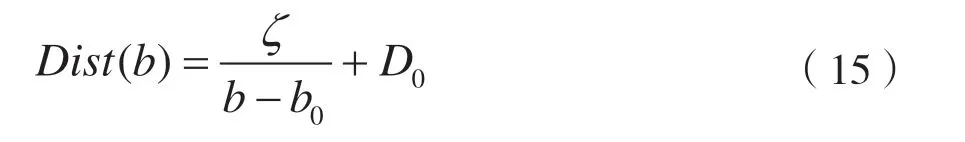
式中：参数ζ、b0和D0可以通过回归技术估计。

式（12）中右边第二项u(dmax-d)为次用户累积等待时间d的单位阶跃函数。当d≥dmax时，其值为零，其中dmax为最大可容忍时延。基于上述回报函数，本文提出的方法可以在最大限度地利用信道的同时平衡切换引起的延迟。

2.2 PPO 模型训练

本文提出的基于PPO 的频谱切换方法的模型结构，如图2 所示。PPO 是基于AC 架构，同样具有策略网络（Actor）和价值网络（Critic），其中策略网络又细分为新策略网络（Actor_new）和旧策略网络（Actor_old）。新策略网络在与环境的交互过程中实时更新，并在一定的训练步数后，将网络参数同步至旧策略网络。

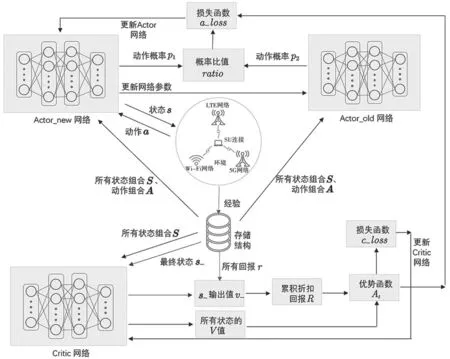
图2 基于PPO 的频谱切换方法的环境模型

模型的具体训练步骤如下。

步骤1：训练开始时随机初始化环境，将环境观测值s输入次用户的Actor_new 网络。Actor_new网络通过softmax 输出相应动作，即选择某一信道的概率。次用户执行最大概率的动作，输入到环境中得到奖励r和下一个状态s_。一个完整的经验(s,a,r,s_)将被存储起来，而后将s_输入到Actor_new 网络，循环执行步骤1，直至存储T个经验。

步骤2：将步骤1 中循环结束得到的最后一个s_输入Critic 网络，得到该状态的价值v_。根据式（16）计算每个时间步的累积折扣奖励Rt：

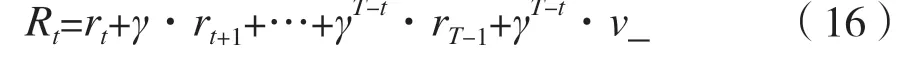
式中：T为总时间步数，即步骤1 中存储的经验数。

步骤3：将存储的所有状态组合S输入Critic网络，得到所有状态的价值V，然后计算各个时间步的优势函数：

步骤4：计算Critic 网络的损失函数c_loss：

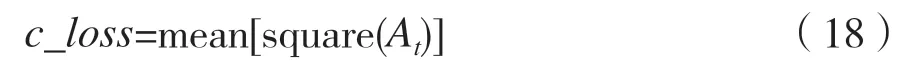
反向传播更新Critic 网络。

基于PPO 的频谱切换算法的伪代码如下：

步骤5：将存储的所有状态组合S、动作组合A分别输入Actor_old 网络和Actor_new 网络，得到每个动作对应的概率p1和p2，用式（11）计算比例值：

步骤6：根据式（10）计算Actor_new 网络的损失函数a_loss，反向传播更新Actor_new 网络。

步骤7：循环m次步骤5 至步骤6，循环结束后将Actor_new 网络的参数同步至Actor_old 网络。

以上步骤1至步骤7为一个训练轮次（Episode）。

2.3 切换算法设计

该算法分为经验收集和网络训练两个阶段。为了避免总是对相同的初始状态做出决策，次用户每次交互都从一个随机的状态开始，以遍历尽可能多的不同场景。次用户采取行动at，即选择一个信道Cat来切换，获得回报r并且状态转移到s_，然后经验(s,a,r,s_)被存储到回放缓冲区中。此处，回报r用式（12）计算。基于PPO 的频谱切换算法中E[W´]和E[W´]+Ts分别是次用户停留在当前通道和切换到另一个信道时的切换时延。当存储区中的经验数达到批次量T时，网络开始利用存储的经验进行训练，更新网络参数（更新步骤详见2.2 节）。更新完毕后，存储区的经验将会被清空，以便进行下一阶段的经验收集。

3 实验仿真和结果分析

实验仿真考虑单一次用户在3 个具有不同ABR信道之间的切换，每个信道都有一个默认的主用户，其到达率服从指数分布。假设主用户到达率为λ，服务时间为E[Xp]，则各信道的忙期概率为ρ=λE[Xp]。模型中价值网络和2 个动作网络都是包含2 个隐层的4 层全连接神经网络，每个隐层包含128 个神经单元。输入层和输出层的神经单元数分别为6 和3，对应状态向量和动作向量的长度。

本文将基于PPO 的频谱切换方法与经典的Q-Learning[7]和近视方法（Myopic）[17]进行比较。采用近视方法的次用户在发生碰撞时总是选择切换到另一个空闲信道。如果有多个空闲通道，次用户选择即时回报最大的信道，否则如果没有空闲通道，次用户将停留在当前通道。由于即时回报与信道的ABR 有关，近视方法与基于模型的方法相似。然而，次用户并不知道主用户到达率、服务时间等其他信道信息。因此，与基于学习的方法如PPO 和Q-Learning 相比，选择即时回报最大通道的短视方法从长期来看可能不是最优的。

图3 将PPO 和Q-Learning 方法的平均轮次回报进行比较。仿真实验共进行了150 轮次，从图3可以看出，PPO 方法具有更快的收敛速度，在第20轮时开始收敛，而Q-Learning 方法在第40 轮时开始收敛。PPO 方法的平均回报曲线较Q-Learning 方法波动更小，证明PPO 方法具有更好的平稳性。此外，PPO 方法的平均回报要高于Q-Learning，证明采用PPO 的频谱切换方法能够使次用户获得更高的传输速率。

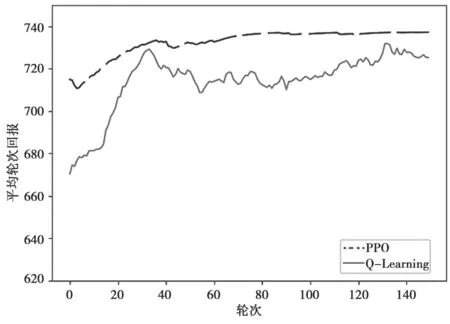
图3 平均轮次回报比较

图4 为信道占用概率比较结果。仿真实验中将3个信道的ABR分别设置为1 Mb/s、2 Mb/s和3 Mb/s。可以看出，信道3 的优势在PPO 方法上得到了很好的体现，次用户对信道3 的占用率高达70%。相比之下，使用Q-Learning 方法的次用户也有选择信道3 的倾向，但它对信道3 的占用概率低于使用PPO方法的次用户。这也解释了图3 中PPO 方法的整体回报大于Q-Learning 方法。

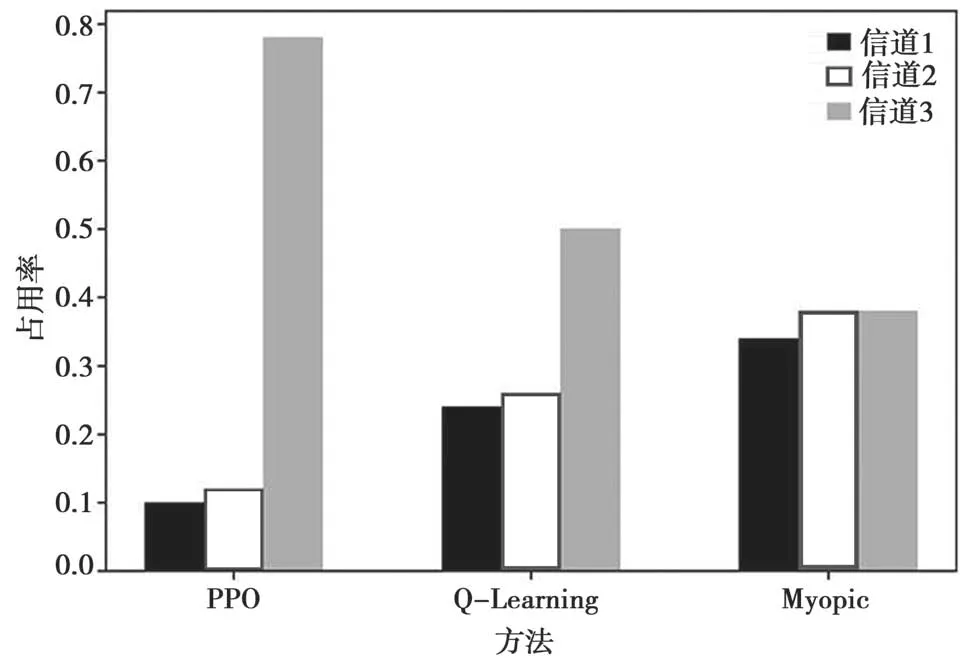
图4 信道占用率比较

图5 选取平均数据传输时间为目标函数与PU忙期进行关系比较。可以看出，所有方法的平均数据交付时间都随着主用户忙期概率ρ的增加而增加。但在相同的条件下，采用PPO 方法的次用户总是能够以最短的时间交付数据。特别是在恶劣的信道条件下（如ρ=0.8），平均交付时间比Q-Learning 方法减少了39.4%，比Myopic 方法减少了40.1%。需要注意的是，由于Always-switch 策略，在传输条件较好的情况下如ρ<0.5 时，近视的性能接近于基于学习的方法。这是因为在ρ较小的情况下，每个信道都可以为次用户提供足够的传输时间。因此，当碰撞发生时可以通过切换信道来减少等待时间。但是，当信道条件较差时，频繁的切换可能会导致更多的等待时间。当ρ>0.6 时，3 种方法的平均数据交付时间迅速上升，这是因为切换次数越多，碰撞频率越高，可用于传输的时间越短。

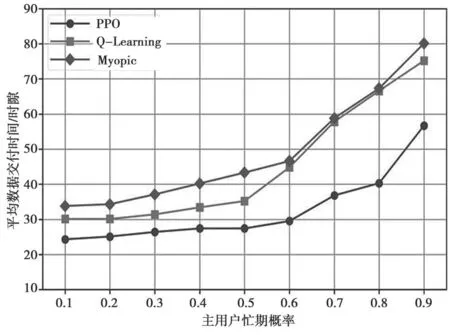
图5 平均数据交付时间比较

图6 选取次用户传输的平均数据交付成功率为目标函数与归一化最大可接受时延进行关系比较。当次用户的数据交付时间大于归一化最大可接受时延时，该数据包将被丢弃。对于一些有延迟约束的应用数据，如视频流，归一化最大可接受时延是一个重要的参数。仿真实验将归一化最大可接受时延从1 至1/6 逐渐减少。结果表明，在相同的归一化最大可接受时延下，PPO 方法能够提高次用户的传输成功率。当归一化最大可接受时延为1/3 时，使用PPO 方法的次用户成功完成数据传输的概率比Q-Learning 方法提高了32.9%，比近视方法提高了64.7%。

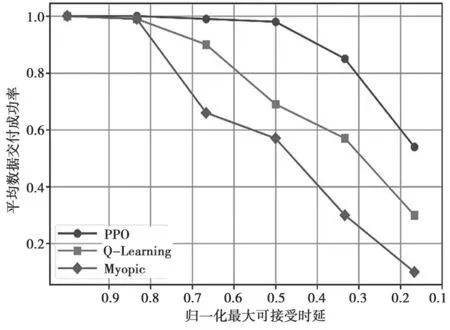
图6 平均数据交付成功率比较

4 结语

本文使用强化学习中的策略梯度算法来解决认知无线网络频谱切换问题，提出了一种基于PPO 的频谱切换方法。该方法通过设计与认知用户QoE 相关的回报函数，能够实现更有效和更准确的切换，更好地利用频谱资源。同时，该方法与传统切换方法相比更注重长期利益最大化，与基于价值函数的强化学习方法（如Q-Learning）相比，具有更好的收敛性和稳定性。仿真实验证明，基于PPO 的频谱切换方法能够带给认知用户更高的数据速率和更少的数据交付时间。