纳入协变量信息的多级计分认知诊断模型
2021-08-28周文杰郭磊
周文杰 郭磊


摘 要 在多级计分协变量认知诊断框架下,提出了一种可同时纳入连续协变量信息和多类别协变量信息的多级计分认知诊断模型GPDM-C,实现了其DINA形态的GPDINA-C的MCMC参数估计。模拟研究的结果显示,GPDINA-C拥有较好的属性/模式判准精度和参数估计能力,相较于未纳入协变量信息的GPDINA,GPDINA-C有更好的模型表现,在参数估计精度上有较大优势。实证研究的结果同样表明,GPDINA-C相比于未纳入协变量信息的多级计分认知诊断模型,能更好拟合实证数据,估计得到的协变量影响参数能客观反映真实情况。
关键词 认知诊断;协变量信息;多级计分认知诊断模型;MCMC
分类号 B841
DOI: 10.16842/j.cnki.issn2095-5588.2021.08.005
1 引言
在心理和教育学研究中,除了感兴趣的变量外,研究人员同时还会收集许多协变量信息,通常包括性别、年龄、地域、家庭社会经济地位等。Li,Hong和Macready(2015)认为协变量信息与我们所关注的建模变量具有重要关系。这些协变量信息常作为调节因子调节自变量对因变量的影响,或是作为控制变量加以控制,许多心理学研究均涉及协变量信息。例如,张莉、薛香娟和赵景欣(2019)以家庭社会经济地位作为协变量控制,构建纵向中介模型,发现农村留守儿童先前的学业成绩能预测随后的歧视知觉,但先前的歧视知觉不能预测随后的学业成绩,并且农村留守儿童的抑郁在学业成绩和歧视知觉之间起纵向中介作用。王玲晓、张丽娅和常淑敏(2019)在控制性别、年级和家庭社会经济地位后,发现母亲拒绝对儿童的同伴拒绝有显著正向预测作用,家庭环境纷杂度调节了母亲拒绝与同伴拒绝之间的关系,儿童外化问题行为在家庭环境纷杂度对母亲拒绝和同伴拒绝关系的调节效应中起完全中介作用。在项目反应理论(item response theory, IRT)中,考虑了协变量的影响后,可以对个体能力的估计和题目参数的估计起到积极作用。研究者们提出了一些纳入协变量信息的项目反应模型,例如,Li等(2015)比较了多种包含协变量信息的混合Rasch模型(mixture rasch model,MRM),发现在MRM中纳入二分类协变量时,被试能力估计精度有所提高,在纳入连续协变量时,被试能力和项目参数的估计都有所提高。Kahraman(2014)使用解释性IRT模型对计算机模拟病例考试(computer-based case simulation test, CCS)考生作答数据进行分析,分别以性别、反应时、项目顺序、选择题得分作为协变量纳入解释性IRT模型中,发现这些协变量信息均能提高模型对数据的拟合度。上述研究均表明,当纳入协变量信息后,模型参数的估计精度将得到提升,更拟合实证数据。
然而,在认知诊断评估(cognitive diagnostic assessment, CDA)相关的研究中,少有研究者考虑了协变量信息的作用。CDA是结合认知心理学和心理测量学优势而开发的新一代测验理论(陈秋梅,张敏强,2010;郭磊,张金明,宋乃庆,2019),可用于评估个体知识掌握结构和加工技能( Leighton & Gierl, 2007),向学生和老师提供个性化指导和反馈(Rupp, Templin & Henson, 2010),受到国内外研究者的广泛关注。认知诊断模型(cognitive diagnostic models, CDMs)作为CDA的关键,可以实现对个体知识状态的估计,正确选择CDM可以有效提高参数估计精度。绝大多数CDMs开发关注如何更好利用个体作答信息和题目信息提升个体知识状态的估计精度,例如为了更加拟合不同题目的属性连接形式而开发的不同屬性连接规则的约束模型(DINA, Junker & Sijtsma, 2001; DINO, Templin & Henson, 2006; LLM, Maris, 1999),以及包含多数约束模型的饱和模型(GDM, von Davier, 2005; LCDM, Henson, Templin, & Willse, 2009; G-DINA, de la Torre, 2011), 能够处理多级计分测验数据的多级计分模型(seq-GDINA, Ma & de la Torre, 2016; GPDM, Chen & de la Torre, 2018; GPCDM,高旭亮,汪大勋,王芳,蔡艳,涂东波,2019),能够处理属性包含多水平信息的多分属性模型(pGDINA, Chen & de la Torre, 2013)。但这些CDMs都忽略了协变量信息的重要作用。
在认知诊断框架下纳入协变量信息不仅可以在宏观层面更好估计个体能力值,还能在微观层面对个体的知识状态实现更精准的分类。研究能够有效提升分类算法精度的模型具有重要意义,因此,很有必要开发可处理协变量信息的CDMs。当前,仅有个别研究探讨了协变量信息在CDMs中的作用。Ayers,Rabe-Hesketh和Nugent(2013)以DINA模型为基础,利用logistic回归表征了协变量信息对属性掌握概率的影响,构建模型如下:
Pik为考生i在属性k上的掌握概率,Malei和Prei分别为考生的性别信息(二分协变量)和前测成绩(连续协变量),βMale和βPre是协变量对掌握概率的影响大小,δk是属性k的难度参数。之后,Park和Lee(2014)提出的协变量DINA模型(the covariate extension of the DINA model)使用协变量信息分别对考生属性掌握概率和题目正确作答概率进行表征,其思路与Ayers等(2013)研究相似。Park,Xing和Lee(2017)构建的解释性认知诊断模型(explanatory CDM)以IRT模型估计得到的能力参数作为潜在变量,与观测变量共同作为协变量表征了属性掌握概率和题目正确作答概率。上述研究结果表明,在加入协变量信息时,提高了个体的属性/模式判准率,以及题目参数的估计精度。
但这些研究存在以下不足,缺乏更广泛的普适性:(1) 从大型测验(PISA,TIMSS,高考)到小型测验(班级测验),这些测验中存在大量多级计分题目(Chen & de la Torre, 2018; Ma & de la Torre, 2016),多级计分题目比二级计分题目能够提供更多信息,而目前的模型均基于二级计分DINA模型开发,不能在多级计分测验中处理协变量信息。(2)这些研究中包含的类别协变量仅为二分变量(如性别),不能处理诸如班级、年级、家庭社会经济地位等多类别协变量信息。因此,本研究旨在开发同时可以处理不同类型协变量的多级计分CDM,以推动CDA在处理协变量信息层面的研究。
2 协变量多级计分认知诊断模型的构建
2.1 基础模型的选择
对多级计分CDMs进行协变量拓广涉及对多级计分CDMs的选择。目前多级计分CDMs包括基于等级反应模型(graded response model)开发的P-DINA (polytomous DINA, 涂冬波, 蔡艳, 戴海琦, 丁树良, 2010)和GPDM(general polytomous diagnosis model, Chen & de la torre, 2018),基于连续比率模型(continuation ratio model)开发的序列GDINA模型(sequential GDINA, Ma & de la Torre, 2016)以及基于分布評分模型(partial-credit model)〖JP3〗开发的GPCDM(general partial credit diagnostic model, 高旭亮等, 2019)等。本研究选择GPDM作为协变量拓广的基础模型,其原因在于:相比于将题目参数设置在累计概率P 瘙 毐 ijc的P-DINA,GPDM将题目参数设置在条件概率Pijc上,这种表示方式更直接(Chen & de la Torre, 2018),因为条件概率Pijc可以直接表示被试i在题目j上得分等级为c的概率,而累计概率P 瘙 毐 ijc表示得分从0至c的概率和,需要通过计算得到对应每个等级的概率值。GPDM、序列GDINA、GPDCDM的加工函数都是GDINA,但仅有GPDM满足GDINA的单调性假设,即掌握更多所需属性的考生不会降低正确作答的可能性(Chen & de la Torre, 2018; Hong, Chang & Tsai, 2016)。同时,GPDM的Q矩阵界定在题目水平上,而序列GDINA与GPCDM均将Q矩阵定义在类别上,
得分步骤顺序要求严格,并且每个类别要求明确地与特定属性相关联,类别Q矩阵不总是适用在现实情境中(Chen & de la Torre, 2018)。
2.2 GPDM-C的测量模型
GPDM-C(the covariate extension of general polytomous diagnosis model)的测量模型本质上等价于GPDM。设诊断测验包含J个题目,考察K个属性,qjk为J×K的Q矩阵中第j行k列元素,取值为1时表示j题考察了属性k,取值为0表示未考察;αik表示被试i是否掌握属性k,掌握为1,未掌握为0;Yij=c表示被试i在题目j上的得分为c,取值为0,1,…,Cj,Cj为题目j的最高得分。于是,GPDM可表示为:
其中,P 瘙 毐 ijc表示被试i在j上得分等于c分数及以上的概率,Pijc则表示被试i在题目j上恰好等于c分的概率;λjc0为题目j分数c上的截距项,表示当被试没有掌握题目所考察的属性时得分为c时的基线参数 ;λjck为题目j分数c在属性k上的主效应,表示当被试多掌握属性k时,对得c分改变的概率;λjckk′为题目j分数c在属性k和k′上的一阶交互效应,表示除掌握属性k和k′对得c分改变的概率之外,两个属性的额外作用;λjc1, …, K为题目j在属性1,…,K上的最高阶交互作用,表示当掌握了所有必要属性时,除了属性主效应和低阶交互效应外导致得c分概率改变的额外影响;ωijk用于判断λjck的存在与否,当题目j考察了属性k的情况下并且被试i掌握了题目j所考察的属性k的水平时ωijk=1,否则为0。当Cj≡1时,GPDM等价于GDINA模型(de la Torre, 2011)。特别地,得0分及以上的概率为P 瘙 毐 ij0=1,得分为Cj+1的概率为P 瘙 毐 ij(Cj+1)=0,易得:∑Cjc=0Pijc=1。
2.3 GPDM-C的结构模型
利用logistic回归用连续协变量信息和分类协变量信息表征属性掌握概率,并将二分类协变量拓展为多类别协变量,表示为:
其中Pik表示被试i掌握属性k的概率;δk为属性k的难度参数,表示属性k的基础难度;Zi为被试i的连续协变量,βk为该连续协变量在属性k上的影响参数;gi表示被试i所属的类别分组;γgik是分组协变量gi的影响参数,代表被试i所属组在属性k上的影响,约束γ1k≡0;αik服从以Pik为概率的伯努利分布。GPDM-C的测量模型和结构模型构成了最终的GPDM-C模型。
2.4 缩减模型GPDINA-C与参数估计
由于GPDM本质是基于GDINA的多级计分拓广,所以GPDM-C也可以约束为各种简约模型以满足不同研究和现实情景的需求。本文基于模型简约性、更易使大众理解的考虑,通过对GPDM-C约束,采用更易理解的题目猜测参数gjc和失误参数sjc,提供一种DINA形式的缩减协变量多级计分模型GPDINA-C,并采用MCMC算法基于R与JAGS软件,对GPDINA-C模型进行参数估计,GPDINA-C的JAGS代码见附录。GPDINA-C的表达式为:
其中gjc是题目j在得分c上的猜测参数,sjc是题目j在得分c上的失误参数,当被试i未掌握题目j所考察的所有属性时,ηij=1且Pijc=gjc,当被试i掌握了题目j所考察的所有属性时,ηij=0且Pijc=1-sjc,其他参数含义同前。尽管本研究以DINA形式为例,但协变量信息可以拓展至其余多级诊断模型中。
3 研究1: 模拟研究
3.1 研究目的
本研究有两个目的:(1)验证MCMC参数估计方法是否能精准估计GPDINA-C的模型参数,即模型的可识别性,以及在多级计分情景下的属性/模式判准率。(2)展示当数据存在协变量影响,而错误使用未能处理协变量信息的诊断模型时,会给参数估计结果带来的影响。
3.2 研究设计
本研究Q矩阵为20题的5属性三级计分Q矩阵(Chen & de la Torre, 2018),见表1。测验长度为2个水平:20题、40题,40题的Q矩阵与20题的Q矩阵是重复关系。题目质量为3个水平:高质量(ηij=1时Pij0从Unif(0.05, 0.15)中生成,ηij=0时Pij0从Unif(0.85, 0.95)中生成)、中等质量(ηij=1时Pij0从Unif(0.15, 0.25)中生成,ηij=0时Pij0从Unif(0.75, 0.85)中生成)、低质量(ηij=1时Pij0从Unif(0.25, 0.35)中生成,ηij=0时Pij0从Unif(0.65, 0.75)中生成),并使Pij1=Pij2=(1-Pij0)2(Chen & de la Torre, 2018;Ma & de la Torre, 2016)。2000名被试的连续协变量从标准正态分布N(0, 1)中生成,将被试随机分到三分类分组协变量中的一组,约束协变量影响在属性水平上相等(Ayers et al., 2013),共包括3个水平:高影响、中影响、低影响,分别表示协变量信息对属性掌握的影响程度,具体设置见表2;参考Ayers等(2013)做法,设置属性难度参数δ=(-1.5, -0.75, 0, 0.75, 1.5)。被试真实掌握情况αik通过公式9和公式10得到。共循环30次,以期求减小随机误差带来的影响。
采用平均误差(bias)和均方根误差(RMSE)作为评价指标来评价GPDINA-C与GPDINA的参数返真性,计算方法分别为bias()=∑Rr=1r-vR和RMSE()=∑Rr=1(r-v)2R,其中r为第r次循环的参数估计值,v为真值,R为总循环数。采用平均属性判准率(AACCR)和模式判準率(PCCR)评价被试知识状态估计的准确性,其计算方法分别为AACCR=∑Ni=1∑Kk=1WikN×K,PCCR=∑Ni=1∏Kk=1WikN,其中当估计得到的ik与真值αik相等时,Wik=1,否则Wik=0。
3.3 结果
3.3.1 GPDINA-C平均属性判准率和模式判准率
如表3所示,当题目质量为高或中等时以及测验长度较长时,GPDINA-C有着较好的属性判准率和模式判准率。纳入协变量信息的GPDINA-C在高质量题目条件下,AACCR和PCCR在20题时的范围分别在0.961~0.970和0.844~0.871,当测验长度增加到40题时,AACCR和PCCR的范围分别提升至0.989~0.992和0.947~0.963;题目质量为中等时,AACCR和PCCR在20题时的范围分别在0.896~0.934和0.622~0.740,当测验长度增加到40题时,AACCR和PCCR的范围分别提升至0.0.952~0.961和0.813~0.841;题目质量为低时,AACCR和PCCR在20题时的范围分别在0.812~0.887和0.382~0.590,当测验长度增加到40题时,AACCR和PCCR的范围分别提升至0.873~0.923和0.552~0.708。题目质量和测验长度大幅度影响了模型的判准率。在相同题目质量情况下,协变量影响越大,模型的判准精度越高。例如,在测验长度均为20题、题目质量均为中等时,在低协变量影响下的AACCR为0.896, PCCR为0.622, 中等协变量影响下的AACCR为0.909, PCCR为0.658, 高协变量影响下的AACCR为0.934, PCCR为0.740。
在所有实验条件下,相比于未纳入协变量信息的GPDINA,GPDINA-C的平均属性判准率和模式判准率都更高,尤其是在题目质量中等或者较差的情况下,该结果表明,当数据受到了协变量影响后,使用未能处理协变量信息的GPDINA模型,将会对被试的知识状态估计精度带来恶化影响。协变量效应也影响了GPDINA-C相较于GPDINA的属性/模式判准精度的提升程度。具体而言,当协变量的影响越大时,GPDINA-C对GPDINA的属性/模式判准精度的提升越大。例如,在测验长度为20题、题目质量均为中等时,在低协变量影响下,AACCR提升了0.07%,PCCR提升了3.7%,在中等协变量影响下,AACCR提升了1.6%,PCCR提升了7.2%,在高协变量影响下,AACCR提升了2.9%,PCCR提升了11.6%;在题目质量均为低时,在低协变量影响下,AACCR提升了2.8%,PCCR提升了13.4%,在中等协变量影响下,AACCR提升了5.8%,PCCR提升了24.0%,在高协变量影响下,AACCR提升了8.0%,PCCR提升了27.4%。以上表明,在有协变量影响的测验中,GPDINA-C能够得到较高的属性/模式判准精度,参数估计方法有效。
3.3.2 GPDINA-C模型题目参数估计精度
如表4所示,GPDINA-C在各实验条件下的题目参数估计精度均较好,bias范围为-0.0017~0.0011,RMSE范围为0.0119~0.0262。在绝大多数情况下,GPDINA-C的题目参数估计精度优于GPDINA,bias更接近0,RMSE更小,说明在有协变量影响的情景下,使用未能处理协变量信息的GPDINA模型,将会降低对题目参数估计的精度,这与前人在IRT领域的研究结果保持一致。当题目质量提高、协变量影响变大或题目长度增加时,GPDINA-C题目参数的估计精度会更好。
3.3.3 GPDINA-C模型结构参数估计精度
如表5所示,GPDINA-C在各实验条件下的结构参数估计精度良好。连续协变量影响参数(β)的bias范围为-0.058~0.045,RMSE范围为0.016~0.068;分类协变量影响参数(γ)的bias范围为-0.086~0.088,RMSE范围为0.053~0.135;属性难度参数(δ)的bias范围为-0.060~0.077,RMSE范围为0.043~0.231。协变量参数(β、γ)的估计精度与题目质量和协变量大小有关,当题目质量越好或协变量影响越小时,协变量参数的估计精度越好。属性难度参数(δ)的估计精度与题目质量和协变量大小有关,当题目质量越好或协变量影响越大时,协变量参数的估计精度越好。
4 研究2: 实证研究
4.1 研究目的
比较GPDINA-C与GPDINA在真实测验中的模型表现,验证纳入协变量信息的多级计分认知诊断模型在实际应用中的优势和适用性。
4.2 实证数据
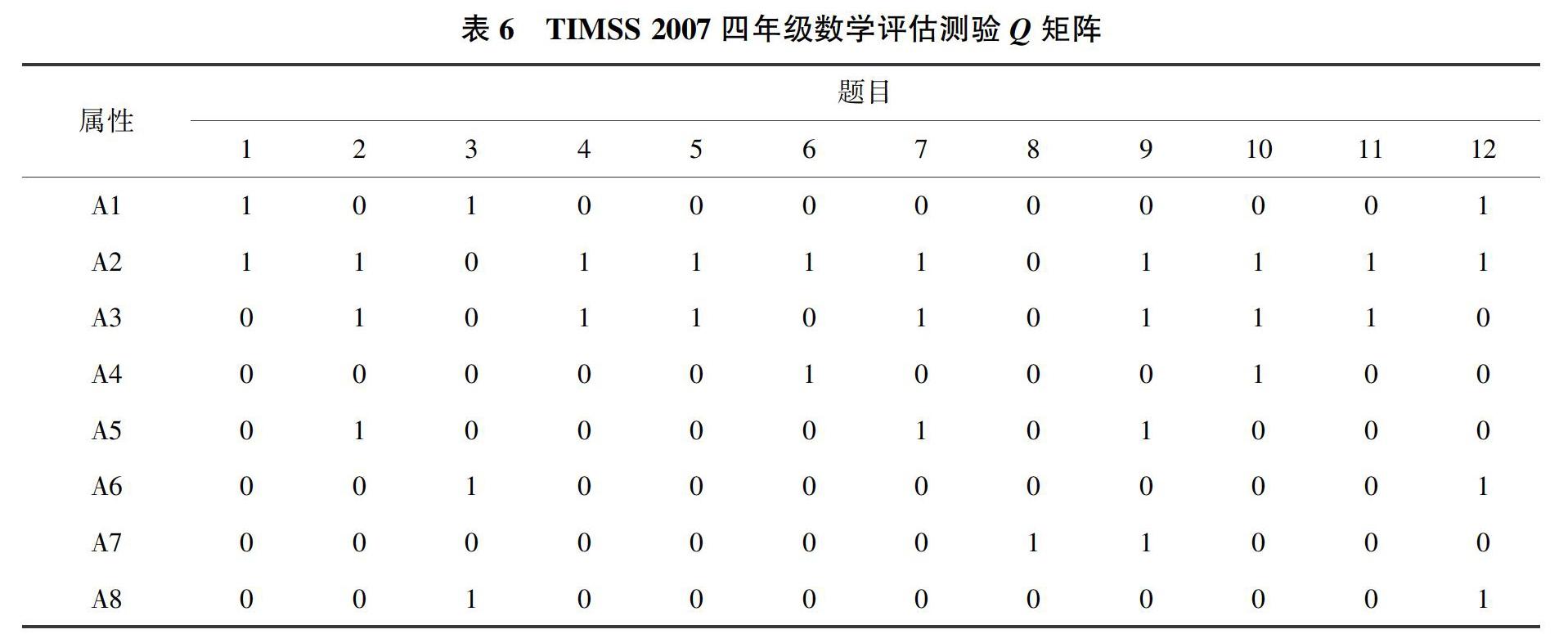
选择国际数学与科学趋势研究(Trends in International Mathematics and Science Study, TIMSS)2007年四年级数学评估测验考生的数据,共有1760名考生,包含10道二级计分题目和2道三级计分题目(第3和第10题)。考察了8个属性,测验Q矩阵由Lee,Park和Taylan(2011)所界定,如表6所示。
Park和Lee(2014)指出,数学和科学具有结构和功能上的关系,数学可以作为科学中的工具,科学也可以进一步刺激数学的发现(Li, Shavelson, Kupermintz, & Ruiz-Primo, 2002),因此,科学成绩可以作为数学成绩的预测变量。在本测验中,考生的数学成绩和科学成绩存在显著正相关(r=0.83,p<0.001),所以本研究选择考生在科学评估测验的标准化成绩作为连续协变量信息用于预测考生的属性掌握程度。分类协变量是考生所在地区,共五组,这些地区的考生成绩有显著的差异(F(4, 1757)=63.64,p<0.001,η2p=0.13),这种地区的成绩差异也能作为被试属性掌握的预测工具。其中,270名考生来自中国香港地区(四年级数学评估测验成绩排名第一),294名考生来自中国台湾地区(排名第三),320名考生来自日本(排名第五),312名考生來自英国(排名第九),564名考生来自美国(排名第十三),美国作为基准组别。
4.3 结果
4.3.1 模型拟合比较
在贝叶斯方法下评价模型数据拟合的指标为偏差信息准则DIC(deviance information criterion),该指标可由JAGS软件直接计算得出,公式如下:
DIC的大小可以判断模型拟合的相对优劣,值越小说明模型对数据更拟合。分析得到,未纳入协变量信息的GPDINA的DIC值为32809.2,纳入协变量信息的GPDINA-C的DIC值为31518.7,说明纳入协变量信息的多级计分模型对这批真实数据的拟合表现更优。
4.3.2 GPDINA-C的协变量参数
GPDINA-C的协变量影响参数β和γ的大小分别反应了连续协变量(科学成绩)与分组协变量(考生所在地区)对考生属性掌握程度的贡献。结果表明,科学成绩对考生属性掌握的影响大小β=2.16(SD=0.11), p<0.001,说明科学成绩可以显著正向预测考生的数学能力掌握程度;表4展示了分组协变量(即地区)对考生属性掌握的影响,即γ参数,以及各地区考生在这12题的平均得分。地区对考生属性掌握的影响与各地区的测验均值有显著正相关(r=0.97,p=0.006),表明GPDINA-C能很好估计分类协变量的取值,GPDINA-C能很好地拟合实际情况中分类协变量对属性掌握的影响作用。以上结果均表明纳入协变量信息的GPDINA-C可以提供GPDINA所不能提供的协变量影响参数信息,并且GPDINA-C能很好估计协变量影响大小,其估计值可以作为协变量影响考生属性掌握的评价指标。
4.3.3 考生知识状态
GPDINA-C从28 =256种知识状态中识别出1760名考生各自所属的知识状态。图6展示了考生数最多的前十类知识状态,属于这十类知识状态的考生占总考生数的95.5%。
5 讨论
5.1 不足与展望
尽管本研究开发了能够处理多种协变量信息的GPDM-C模型,并给出其简约模型GPDINA-C的参数估计的MCMC算法,但仍有一些值得完善和思考的研究方向。
(1) 在实证研究中,何时需要考虑协变量的信息,本研究给出如下建议:若协变量与测验所考察能力或属性有显著的相关关系,此时可以将该协变量信息纳入认知诊断模型中,在控制协变量信息的基础上,提高认知诊断模型的估计精度;若协变量与属性之间不存在相关关系,可以不纳入协变量,这也是结构方程模型,纵向数据分析,项目反应理论等研究中的常见做法。此外,也可从模型与数据拟合指标的角度去判断协变量信息是否应纳入,若纳入协变量信息后模型拟合指标变小,则说明纳入协变量信息后,模型更加拟合该批数据,理应纳入协变量信息,获得更精确的估计结果;反之则可以不纳入协变量。考虑到文章篇幅和研究的聚焦性,本研究未以GPDINA作为真模型进行探讨,未来可尝试模型的交叉比较。
(2) GPDM-C是对以等级计分思想为基础的GPDM进行的开发,而目前存在如基于连续比率模型(continuation ratio model)的seq-GDINA,基于分布评分模型(partial-credit model)的GPDCDM等其他多级计分思想的模型,它们的计分逻辑不同,未来可基于不同计分逻辑探讨纳入协变量的影响。
(3) 本研究在模拟和实证研究中约束了模型中的协变量影响参数(β,γ)在属性水平上相等,即协变量在所有属性上有相同的作用,这更适用于属性粒度较小的测验,例如同一个协变量对小属性加法和减法的掌握程度的影响相似,而可能不适用于属性粒度较大的测验;同一个协变量对大属性数学和语文的掌握程度的影响差異很大。未来研究中可以放松该限制,考察协变量在各属性上的不同影响。
(4) 本研究涉及的协变量仅为一种连续协变量信息和一种类别协变量信息的影响,而在现实测验情境下,研究者收集了大量协变量信息,未来可以探讨纳入更多协变量信息时模型的表现,以及加入协变量交互作用时模型的表现。
(5) GPDM-C设定的协变量影响在属性水平,即协变量影响属性掌握程度,从而影响考生作答情况。当前还存在将协变量影响直接作用于考生作答水平的建模思路(Park & Lee, 2014; Park at al., 2017),未来还可以在多级计分框架下,探讨协变量影响分别在属性水平和作答水平时对模型表现的影响。
(6) 实际中存在大量多分属性的测验情景(郭磊, 张金明, 宋乃庆, 2019; Chen & de la Torre, 2013), 纳入协变量信息可以在属性的多个水平上产生不同影响效果,所以在多分属性认知诊断模型中纳入协变量信息也值得进一步探讨。
5.2 研究结论
本研究在多级计分认知诊断框架下开发了一种同时纳入连续协变量信息和多类别分类协变量信息的新模型GPDM-C,并实现了其约束模型GPDINA-C的MCMC参数估计,通过模拟研究验证了GPDINA-C模型性能,最后通过TIMSS测验(2007)的实证数据验证了GPDINA-C在实际应用中的效果,验证了纳入协变量信息的GPDINA-C相比于传统多级计分认知诊断模型的优势。主要研究结论如下。
(1) MCMC参数估计程序表现优良,能精确估计GPDINA-C模型的所有参数。
(2) 模拟研究发现,GPDINA-C有较好的判准精度表现。在有协变量影响的情景下,使用不能处理协变量信息的认知诊断模型将会对考生知识状态的判准精度产生负面影响,尤其是在中等或较差题目质量的情况下,相比于GPDINA-C,未纳入协变量的GPDINA的判准精度大幅降低。
(3) GPDINA-C题目参数估计精度较好,在有协变量影响的情景下,使用不能处理协变量信息的认知诊断模型将会对题目参数估计产生负面影响,GPDINA-C的协变量参数(β,γ)与属性难度参数(δ)都有着较好的参数估计表现。
(4) 题目质量和协变量影响的大小影响了参数估计的精度,题目质量越好或协变量影响越大时,参数的估计精度越高。
(5) 实证研究发现, GPDINA-C相比于未纳入协变量信息的GPDINA而言,对实证数据的拟合程度更好,GPDINA-C可以提供GPDINA所没有的协变量影响参数,并且协变量影响参数能较好地反映真实的协变量影响情况,值得在实际应用中推广。
参考文献
陈秋梅, 张敏强 (2010). 认知诊断模型发展及其应用方法述评. 心理科学进展, 18(3), 522-529.
郭磊, 张金明, 宋乃庆 (2019). 整合后验信息的多分属性认知诊断信效度指标. 心理科学, 42(2), 446-454.
高旭亮, 汪大勋, 王芳, 蔡艳, 涂冬波 (2019). 基于分部评分模型思路的多级评分认知诊断模型开发. 心理学报, 51(12), 1386-1397.
王玲晓, 张丽娅, 常淑敏 (2019). 儿童母亲拒绝与同伴拒绝的关系——一个有中介的调节模型. 心理科学, 42(6), 1347-1353.
张莉, 薛香娟, 赵景欣 (2019). 歧视知觉、抑郁和农村留守儿童的学业成绩:纵向中介模型. 心理科学, 42(3), 584-590.
Ayers, E., Rabe-Hesketh, S., & Nugent, R. (2013). Incorporating student covariates in cognitive diagnosis models. Journal of Classification, 30(2), 195-224.
Chen, J., & de la Torre, J. (2013). Ageneral cognitive diagnosis model for expert-defined polytomous attributes. Applied Psychological Measurement, 37(6), 419-437.
Chen, J., de la Torre, J. (2018). Introducing thegeneral polytomous diagnosis modeling framework. Frontiers in Psychology, 9, 1474.
de la Torre, J. (2011). The generalized DINA model framework. Psychometrika, 76(3), 179-199.
Henson, R. A., Templin, J. L., & Willse, J. T. (2009). Defining a family of cognitive diagnosis models using log-linear models with latent variables. Psychometrika, 74(2), 191-210.
Hong, C.Y., Chang, Y.W., and Tsai, R.C. (2016). Estimation of generalized DINA model with order restrictions. Journal of Classification, 33(3), 460-484.
Lee, Y., Park, Y. S., Taylan, D. (2011). Acognitive diagnostic modeling of attribute mastery in Massachusetts, Minnesota, and the U. S. national sample using the TIMSS 2007. International Journal of Testing, 11(2), 144-177.
Leighton, J. P., & Gierl, M. J. (2007). Cognitive diagnostic assessment for education-theory and applications. Cambridge: Cambridge University Press.
Li, M., Shavelson, R. J., Kupermintz, H., & Ruiz-Primo, M. A. (2002). On the relationship between mathematics and science achievement in the United States. In D. F. Robitaille & A. E. Beaton (Eds.), Secondary analysis of the TIMSS data (pp. 233-249). Norwell, MA: Kluwer Academic Publisher.
Li, T., Jiao, H., Macready, G. B. (2016). Differentapproaches to covariate inclusion in the mixture rasch model. Educational and Psychological Measurement, 76(5), 848-872.
Maris, E. (1999). Estimating multiple classification latent class models. Psychometrika, 64(2), 187-212.
Ma, W., & de la Torre, J. (2016). A sequential cognitive diagnosis model for polytomous responses. British Journal of Mathematical and Statistical Psychology, 69(3), 253-275.
Junker, B. W., & Sijtsma, K. (2001). Cognitive assessment models with few assumptions, and connections with nonparametric item response theory. Applied Psychological Measurement, 25(3), 258-272.
Kahraman, N. (2014). An explanatory item response theory approach for a computer-based case simulation test. Eurasian Journal of Educational Research, 14(54), 117-134.
Rupp, A., Templin, J., Henson, R. A. (2010). Diagnostic measurement: Theory, methods, and applications.New York: Guilford Press.
Templin, J. L., & Henson, R. A. (2006). Measurement of psychological disorders using cognitive diagnosis models. Psychological Methods, 11(3), 287-305.
Park, Y. S., & Lee, Y. (2014). Anextension of the DINA model using covariates: Examining factors affecting response probability and latent classification. Applied Psychological Measurement, 38(5), 376-390.
Park, Y. S., Xing, K., Lee, Y. (2017). Explanatorycognitive diagnostic models: Incorporating latent and observed predictors. Applied Psychological Measurement, 42(5), 376-392.
vonDavier, M. (2005). A general diagnostic model applied to language testing data(ETS Research Report no. RR-05-16). Princeton, NJ: Educational Testing Service.
Incorporating Covariates Information in Polytomous Responses Cognitive Diagnosis Model
ZHOU Wenjie1, GUO Lei1,2
(1 Faculty of Psychology, Southwest University, Chongqing 400715, China)
(2 Southwest University Branch, Collaborative Innovation Center of Assessment toward Basic Education Quality, Chongqing 400715, China)
Abstract
Covariates play an important role in psychological and educational studies, which can be used as control variables or regulatory factors in modelling. A few studies involve covariates information in Cognitive diagnosis models (CDMs). However, these studies have some issues that need to be solved. First, the current covariate extension models cannot analyze these polytomous responses. Second, the category covariates included in these studies are only dichotomous variables (such as gender). It cannot handle multi-category covariate information, such as grade and family socioeconomic status.
This paper proposed the GPDM-C (The covariate extension of General polytomous diagnosis model) that incorporates both continuous and multi-category covariates in the polytomous response cognitive diagnosis framework. For simplicity, the saturated GPDM-C model was constrained as a reduced model, named the GPDINA-C model. MCMC algorithm was implemented in JAGS software to complete parameter estimation.
In order to evaluate the parameter estimation accuracy of the GPDINA-C model, showing the advantages of incorporatingcovariates in the polytomous responses model, three factors (item quality, test length, and covariates effect size) were considered in a simulation study. The results indicated that: (1) The MCMC algorithm can accurately estimate all GPDINA-C model parameters. (2) Both person parameters and structure parameters recovery of GPDINA-C outperform the recovery of GPDINA.
Finally, an empirical research is applied to examine the performance of the GPDINA-C model in practice. The results indicate that GPDINA-C hada smaller DIC value than the GPDINA model did, which manifests that the GPDINA-C had a better fit for this empirical data. Furthermore, the covariates parameters of the GPDINA-C can infer the influence of covariates on attribute mastery objectively.
Key words: cognitive diagnosis; covariates information; polytomous responses cognitive diagnosis model; MCMC
