一种洛伦兹力微机械谐振磁传感器建模及数值仿真∗

刘 恒，张 玉，舒进华，杨添熠

(南京信息工程大学电子与信息工程学院，江苏 南京 210044)

磁性传感技术由于不受环境的湿度、污垢、油脂、灰尘以及安装振动的影响，因此磁传感器在电子仪器仪表和工业设备中有着广泛的应用，如铁磁材料剩余应力检测、缺陷定位、磁共振成像、流程工业、煤矿勘探、电流测量和等方面[1－2]。基于MEMS的磁传感器具有体积小、功耗低、成本低、性能稳定、批量生产和高灵敏等优点[1]，传感器制备材料以硅为主，克服了磁传感器制备须采用特殊磁性材料及其对被测磁场的影响。基于洛伦兹(Lorentz)力的微机械谐振式磁传感器通过电容、压阻和光学感测技术来检测磁场。电容检测通过表面或体硅微加工工艺实现，将待测磁场转换为电信号输出。表面工艺允许电子电路与磁传感器制作在同一芯片上，温度依赖性较小[3]。但谐振微结构在常压封装下有大的空气阻尼，需要真空封装才能提高传感器灵敏度。压阻检测适于采用体微加工工艺实现和简单的信号处理系统，但输出电阻易受温度影响导致存在电压偏移，系统中需额外温度补偿电路。利用光敏检测技术制备的磁传感器具有抗电磁干扰的特性，系统需要测控电路比其他两种的少，但检测系统存在体积大、难集成缺点。上述检测技术都存在着由焦耳效应而导致传感器结构发热谐振频率漂移问题，因此测控电路需跟踪谐振频率的变化来维持传感器工作在谐振状态[4]。

在微机械谐振式传感器模拟驱动控制中，有锁相环频率跟踪和自激振荡驱动两种方案[5－6]。锁相环频率跟踪控制利用交流电压作用于驱动结构上产生交变的静电力来激励结构振动，利用鉴相器来比较驱动电压和检测振动信号的相位差，当相位差不满足期望值时调整驱动电压频率直至满足相位差要求。品质因数较小时，频率调整时间较长，传感器动态性能受到压控振荡器初始频率和滤波器等影响。需配合微机械谐振传感器的固有频率来对集成的锁相环芯片选型。自激振荡利用上电随机噪声产生静电力来激励微结构振梁，在真空封装下，微结构等效为一个高品质因数的带通滤波器，通过不断的反馈来增大静电驱动力和振动幅度[7]。品质因数越大，选频特性越好，频率跟踪特性更好[8]。品质因数小，难起振稳定。本文设计了一种洛伦兹力微机械谐振磁传感器，并推导了传感器灵敏度解析表达式，针对传感器频率跟踪要求，分析基于锁相环的频率跟踪电路并利用平均周期法分析了电路稳定性要求及结构、电路参数对频率跟踪的影响。

1 洛伦兹力微机械谐振磁传感器

洛伦兹力微机械谐振式磁场传感器表芯包括结构层和电极层。结构层包括上下、左右对称的四个支撑结构振动的锚点F41、F42、F43、F44，4个多级折叠梁E31、E32、E33、E34分别依附于4个锚点上悬空。一个倒“工”字型的微机构质量块M的4个末端分别与4个多级折叠梁连接。在支撑梁的支撑下，质量块悬空，质量块有阻尼孔，上下、左右对称，质量块垂直方向附有悬空平板。检测电容4个锚点D21、D22、D23、D24固定，4个锚点分别连接有悬空的平板，质量块附着的平板与检测电容锚点连接的平板构成检测电容，其中D21和D22为上下对称的一组，D23和D24也为上下对称的一组，当质量块M沿X轴左右移动时，一组电容增大，则另一组电容减小，构成差分检测电容对。质量块M左右振动时，为了限制折叠梁幅度过大失效，A1和A2为对应的水平止档锚点，在A1和A2的中部设置有止档板，结构层见图1。

图1 洛伦兹力微机械谐振传感器结构层示意图

洛伦兹力微机械谐振传感器在应用中电极连接及接口电路见图2，锚点F41和F43通过电极层连接在一起，锚点F42和F44通过电极层也连接在一起；检测电容锚点D21和D22也通过电极层连接，D23和D24也连接。当存在沿X轴方向的磁场时，直流偏置电压V B与交流电压V C(t)差分偏置作用于上下两组锚点上，连接见图2。当存在垂直纸面方向变化磁场B时，微结构存在Y轴方向的自上向下电流，根据左手定则，质量块M受到洛伦兹力的作用左右振动。

图2 洛伦兹力微机械谐振传感器接口电路

根据原理，质量块M受到的洛伦兹力F(t)为:

式中:B(t)为待测磁场，T；i(t)为电流，A；L为电流在垂直方向的微结构长度，m，微结构尺寸和电压加载方式确定后，L就为已知量。在洛伦兹力作用下，微结构振动位移x(t)，m，有:

式中:m为微结构的模态质量，kg；c为封装后的阻尼系数；k为4个多级折叠梁的等效刚度，N/m。微结构的固有谐振频率f0，Hz，ωn为角频率，rad/s，表示为:

当激励电流频率与微机构固有频率一致时，微结构振动位移x(t)表示为:

式中:Q为封装后的品质因数，反比于阻尼系数c。微结构质量块M上的平板与检测电容锚点上的平板构成差分检测电容。差分检测电容C1对应左边上下电容对，检测电容C2对应右边上下电容对，检测电容表示为:

对应差分检测电容ΔC为:

式(5)～式(7)中:N为检测电容平板对数量，ε为空气介电常数，S为1对平板的交叠正对面积，m2；d0为平板对初始极板间距，m。检测电容通过电荷放大器和差分放大器输出对应电压V0(t)。

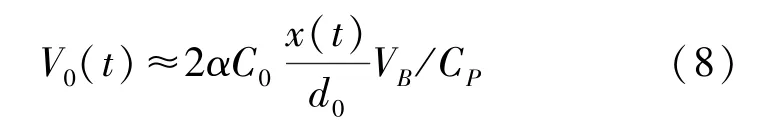
式中:C P为接口电荷放大器反馈电容，F；α为差分放大器的比例放大系数。当微结构和接口电路等效电阻为R时，对应流过微结构的电流i(t)为:

结合式(1)、(4)、(8)、(9)，微结构谐振状态下输出电压V0(t)为:

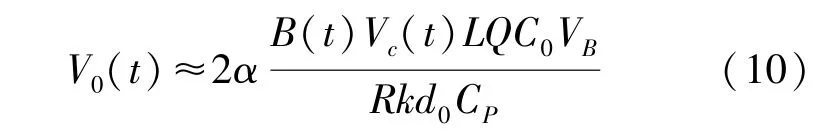
式(10)对待测磁场B(t)求导，得到灵敏度β，V/T为:

根据式(11)有，灵敏度β与微结构本身的折叠梁刚度k，封装制品因数Q，初始检测电容C0，平板间距d0，电流方向的微结构长度L，微结构接口等效电阻R有关。封装后可以通过调节反馈电容C P，加载的直流偏置电压V B与交流电压V C(t)的幅值及差分放大器的放大系数α来改变灵敏度。传感器要求输出具有良好的线性度，就要求控制上述参数不变。

2 基于锁相环的传感器谐振频率跟踪控制

洛伦兹力微机械谐振磁传感器需要测控电路维持微机械谐振，测控电路产生的洛伦兹力变化频率跟踪微结构由于应力、温度、振动幅度与频率的耦合等导致的谐振频率漂移。基于锁相环的测控电路信号转换图见图3，微结构在洛伦兹力作用下发生振动产生位移，通过检测电容将结构位移转换为检测电容变化，通过电荷放大器和差分放大器实现检测电压的输出。输出电压为正余弦变化的电信号，差分放大器调节增益系数α得到锁相环需要的电压幅值。锁相环(Phase lock loop)一般包括3个模块:鉴相器(PD)、低通滤波器(LPF)、压控振荡器(VCO)。由于洛伦兹力与微结构振动位移相位差为90°，锁相环实现输出电压V0(t)与驱动交流V C(t)保持90°相位差。压控振荡器输出幅度恒定的余弦波电压加载在微结构上。

图3 洛伦兹力微机械谐振传感器信号转换图

为了便于分析，将图3所示的信号转换合并，得到图4的动力学分析框图，在接口电路基础上增加了锁相环。为了改善频率跟踪的动态特性，在滤波器后增加了积分环节。

图4 洛伦兹力微机械谐振传感器系统分析模型

根据图4，洛伦兹力F(t):

式中:V d、θ、ω依次为压控振荡器输出的交流电压的幅度、相位、频率，F为洛伦兹力的幅度，可表示为:

当待测磁场在某时刻确定时，其他参数也确定，F是固定的。压控振荡器相位θ为:

式中:z为输入受控电压，kvco是电压－频率转换系数，在限定范围内，压控振荡器输出电压的频率与输入控制电压有线性关系，ω0为压控振荡器初始角频率。相位θ表示为:

相位差经过积分控制器调节后有:

式中:k I为积分系数，控制器调节性能参数。鉴相器为异或门，u1(t)、u2(t)为输入信号，UP和DOWN为输出。鉴相器输出方波幅度为U d，输入信号相位差为ϕ，y为滤波器输出信号，为滤波时间常数，有:

根据图4及式(12－17)，系统的动力学方程为:

假设振动位移x(t)为幅度和相位时变的[9]，有:

结合式(19)和方程组(18)，求解有:

结合慢时变系统的特性，用平均周期法近似化简式(20)和(21)，有:

对式(16)、式(17)、式(22)、式(23)关于时间t求导并令为0，有平衡点:

对式(24)除以B(t)就得到传感器的灵敏度，灵敏度与微结构等效刚度k、谐振频率ωn等有关。在平衡点对方程组(18)线性化，Jacobian矩阵为:

矩阵对应特征方程为:

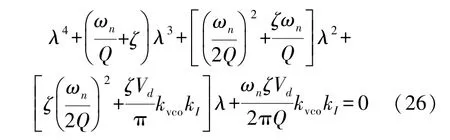
式中:特征值为λ。根据劳思判据，系统稳定条件是各系数大于0，同时满足:

化简求解后有:

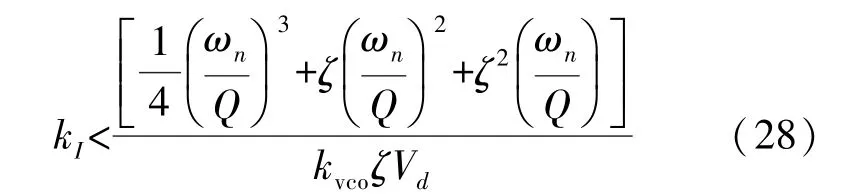
改变积分控制器的系数k I来调节系统的稳定性。分析不同系数下特征值在s平面上分布情况可确定积分系数对改变系统的动态性能的影响。在k I为0时，系统具有四个极点，分别是:s1＝－ζ，s2＝－ωn/2Q，s3＝－ωn/2Q，s4＝0，其中极点s2为固定的极点，在k I增大的过程中，极点s1不断远离虚轴，系统响应时间变短，其他各极点也将不断变化，达到临界值后将出现跟踪频率的振荡。

3 微机械谐振式磁传感器的闭环数值仿真

为了对平均周期法定量分析的锁相环频率跟踪测控电路进行验证，在MATLAB/Simulink下建立锁相环频率跟踪测控电路数值模型。微结构参数根据版图设计确定，微结构层由单晶硅掺杂浓硼深刻蚀，电极层由金溅射到玻璃上，结构层和电极层通过阳极键合在一起[10]。封装环境为低真空度封装，有限元仿真确定封装品质因数，数值模型仿真见图5，模型参数见表1。

图5 洛伦兹力微机械谐振磁场传感器仿真模型

表1 传感器及测控电路参数

根据式(28)，结合图5和表1参数计算得到临界k I为17.76。由于微结构在振动中存在温度的变化造成谐振频率的偏移[11]，等效为结构刚度的变化。在数值模型中加入了振梁机械刚度在2 s由0阶跃变化到40 N/m，见图6，测试系统频率跟踪的性能[12]。

图6 刚度扰动

外部磁场输入利用仿真时钟叠加进入并线性增大，在仿真时间5 s内由0逐渐增加到1.25 T，见图7，模拟外部不断变化的磁场。

图7 输入的待测磁场

图8为k I为15时的频率跟踪仿真曲线，满足约束等式(27)，在刚度扰动下，谐振频率从10 kHz变化到8.944 kHz，频率跟踪曲线稳定；图9为k I为30时的频率跟踪仿真曲线，不满足约束等式(27)，频率跟踪曲线一直振荡，微结构幅度振荡，k I越大，振荡越厉害，仿真与理论分析一致。

图8 满足约束条件的频率跟踪(k I＝15)

图9 不满足约束条件的频率跟踪(k I＝30)

图10为满足约束等式的鉴相器输出电压，在2 s前，频率跟踪稳定，相位差恒定；当频率跳变后，鉴相器相位差发生变化，测控电路不断调整直到差值恒定。图11为对应的激励交流电压，幅度恒定5 V，但频率根据微结构谐振频率变化。鉴相器差值和交流驱动电压的仿真与电路期望一致，验证理论分析正确性。

图10 鉴相器对应的相位差

图11 激励交流电压

在图6的刚度扰动和图7的待测电场激励下，图12为检测输出电压，中间线为仿真输出时域电压曲线，边缘顶线(理论)为根据平衡点¯a0计算的幅值；图13为激励磁场反向减小对应检测输出电压，中间线为仿真的时域电压曲线，边缘顶线(理论)为平衡点¯a0计算的幅值，两种情况仿真和理论分析完全一致，在2 s处均存在频率跟踪的渐稳现象。

图12 微结构在不同磁场下的谐振幅度(正向)

图13 微结构在不同磁场下的谐振幅度(反向)

在满足式(28)且压控振荡器初始频率ω0不同，初始频率越小，跟踪稳定时间越长，频率稳定后，再次跟踪过程相同，频率跟踪过程见图14；当积分系数k I满足式(28)，积分系数越小，跟踪时间越长，见图15，积分系数太小，难以满足快速跟踪要求；滤波器时间常数ξ越小，滤波特性越好，过大的时间常数会导致频率跟踪的过冲及振荡，见图16。仿真实验表明平均周期法分析鉴相器为异或门的锁相环测控电路的正确性，为后续硬件电路调试提供了基础。

图14 不同初始频率的频率跟踪

图15 不同积分系数的频率跟踪

图16 不同滤波器时间常数的频率跟踪

4 结论

建立了洛伦兹力微机械谐振式磁传感器的动力学分析模型，并针对设计的传感器建立了鉴相器为异或门的锁相环测控电路数值仿真模型。针对传感器系统的高阶和非线性问题，利用平均周期法结合各模块的状态方程，推导了频率跟踪的锁相环积分器约束条件和系统稳态平衡点。数值仿真实验定量的验证了频率的跟踪稳定需满足积分系数的约束要求，同时与接口电路的一些参数无关，稳态平衡点的仿真结果与理论分析一致。频率跟踪动态过程与压控振荡器初始频率ω0、积分系数k I、滤波器时间常数ξ有关。