基于LMD-SVD和极限学习机的滚动轴承故障诊断方法研究
2021-08-28孟祥川许同乐
刘 洋,孟祥川,许同乐
(山东理工大学机械工程学院,山东 淄博 255049)
1 引言
滚动轴承是高温风机的重要部件,也是易损件。风机故障中与轴承损伤有关的几乎占到了三成[1、2],因此对风机轴承故障诊断是非常有必要的。传统的滚动轴承诊断方法主要是快速傅里叶变换,然而在非平稳、非线性工况下故障信号效果不佳。针对振动信号为非线性、非平稳信号的情形,国内外学者提出一些常用的时频分析方法,例如小波包变换(WPT)、经验模式分解(EMD)、HHT[3-5]。WPT具有在时频域提供局部特征和识别振动信号突变分量的特性,但WPT本质上是一个可调窗口傅立叶变换,并非每个分解分量的所有瞬时频率都具有物理意义,WPT计算时间冗长,当数据量较大时难以实现;EMD是一种自适应信号处理方法,可以将信号分解为一系列正交分量,成为本征模函数,再基于本征模函数进行希尔伯特变换,得到信号的全能量-频率-时间分布;HHT是EMD与希尔伯特变换的结合,由于EMD与HHT均有自适应分解的特点,在机械故障检测领域得到广泛应用。但是,EMD存在过度包络、模式混淆等缺陷,且HHT获得的负频率可解释性差。局部均值分解(LMD)是由Smith于2005年提出的,LMD适于将非线性和非平稳振动信号自适应分解为一系列乘积函数,每个乘积函数是包络信号和具有物理意义的瞬时频率的纯调频信号的乘积。LMD形式上与EMD相似,但已证明LMD在某些方面优于EMD,如信号更好的局部特征和时间尺度以及抵抗过冲影响的能力,并且需要更少的解码组件。
将采用LMD方法从复杂滚动轴承振动信号里提取出变工况下的故障特征,但是基于LMD得到的PF分量对于分类方法的输入而言过大,为解决这一问题,引入奇异值分解(SVD)来压缩故障特征向量的尺度,从而提高特征向量的鲁棒性。极限学习机(ELM)是一种机器学习算法,在大量回归分析中得到应用,相比支持向量机(SVM)需要更少的人为干预,运行时间也更少,分类精度也更高。将采用ELM方法对滚动轴承进行不同工况下的故障状态分类。
2算法分析
2.1 LMD算法
LMD算法在局部均值计算、分解分量、瞬时频率计算等方面具有一定的优越性,且没有严重的端点效应。为了从振动信号中提取故障信息,LMD算法可以将原始信号分解为一系列单分量调频调幅信号(PF),PF的物理意义是包络信号与调频信号的乘积,进而可以导出瞬时频率,LMD是通过逐步滑移信号实现的[6-8]。通过分解过程,原始信号可以根据下式重构:

原始信号x(t)可以由所有的PF和单调函数uk进行重构,说明LMD可以保证原始信号的完整性,进而可以提取出完整的故障信息[9、10]。并且LMD得到的分解分量少,这一优势可以保证特征信息不会被分割成多个相邻的分解层[11]。但是基于LMD得到的PF分量对于分类方法的输入而言太大了,为了解决这一问题,本研究引入奇异值分解(SVD)来压缩分解分量的尺度。
2.2 SVD理论
SVD是基于相空间重构的降噪方法,通过对一维时间序列实现Takens相空间重构,得到重构维数p和延迟步长q。再对重构以后的矩阵实现奇异值分解,从而基于噪声和信号的能量可分性,达到降噪目的。奇异值是矩阵的固有特征,稳定性好,即便矩阵中某个元素发生改变,矩阵奇异值变动很小,同时矩阵奇异值还具备比例不变与旋转不变性质。总而言之,矩阵奇异值满足模式识别的特征要求。
设原始信号采样点数量为n,真实PF分量的个数等于m,那么可以得到m×n的矩阵X,X的SVD如下式:

式中:U、V—m阶与n阶的正交方阵;S—m×n阶的斜对角矩阵,其中,σ=diag(σ1,σ2,σ3,...,σr)),σi—矩阵的奇异值,且均不小于0。
从上式可以看出,X可以看作特征向量ui,vT i作外积以后与奇异值的加权和,权重是非零奇异值。权重越大,则特征向量在重建信号中所占比例越大。
基于LMD-SVD特征提取的主要流程如下:
(1)对信号x*(t)实现LMD分解,获得频率由高而低的若干PFi(i=1,2,...,n)分量;
(2)通过相关系数与方差贡献率得到起主导作用的PF分量,并构成特征矩阵X;
(3)对特征矩阵X进行SVD分解,获得相应奇异值,即为滚动轴承信号的特征向量。
2.3极限学习机
文献[12]最初提出的极限学习机(Extreme Learning Machine,ELM)是针对单隐层前馈神经网络开发的,然后扩展到“广义”单隐层前馈网络(SLFN)。ELM是一种新的学习算法,具有更快的学习速度和更好的泛化性能[13]。SLFN结构,如图1所示。
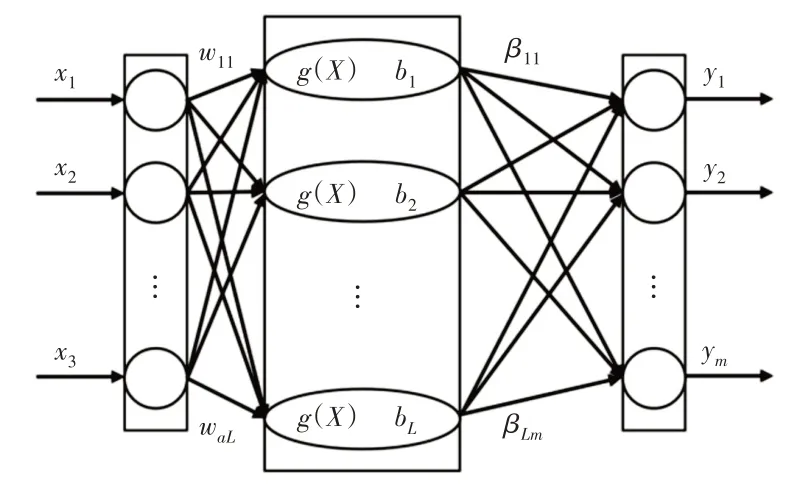
图1单隐层前馈网络结构Fig.1 Single Hidden Layer Feedforward Network Structure
图中:Xi—输入样本—输入层中所有节点之间的链路权重向量;g(x)—隐藏层中神经元的激活函数;bi—阈值。隐藏层中的神经元隐藏层中的第i个节点和输出层中的所有节点之间的链路权重向量;yi—网络的输出;n—输入层中的节点数量;L—隐含层中的节点数量;m—输出层中的节点数,j=1,2,…,n。
ELM的数学模型如下描述:
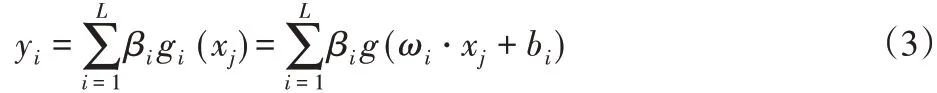
ELM对激活函数g(x)不敏感,而且几乎所有满足ELM泛逼近能力定理的非线性分段连续函数都可以作为激活函数[14]。例如:


图2基于LMD-SVD和极限学习机的滚动轴承故障诊断方法流程Fig.2 Fault Diagnosis Process of Rolling Bearing based on LMD-SVD and Extreme Learning Machine
Sigmoid函数是前馈神经网络中的主要激活函数,具有硬极限函数和多二次函数的ELM也具有良好的性能。在研究中,选择Sigmoid函数作为激活函数。ELM算法流程如下:(1)确定隐层神经元数目L和激活函数g(x),随机分配i、b i和βi;(2)计算隐层输出向量;(3)计算输出权重β̂。
3 基于LMD-SVD和极限学习机的滚动轴承故障诊断方法
轴承故障诊断总流程图,如图2所示。
3.1 实验数据采集
本研究实验采用的轴承实验系统由功率为1470W的电动机、试验轴承、扭矩传感器和电气控制装置组成,轴承转速为1750r∕min。数据采集卡采用NIPCI-4472,采样频率设定在12000Hz。加速度传感器安装在电动机的驱动端以获取轴承的振动信号,轴承尺寸内径25mm、外径52mm、宽度15mm。故障的引入采用电火花加工方法。试验滚动轴承为SKF公司的6205-RS深沟球轴承。试验台由2马力电机、液力变矩器∕编码器、测功机和控制电路组成。采用安装在磁基壳上的加速器传感器,采集正常、内圈故障、外圈故障和滚动体故障等振动信号。针对各种故障模式在不同运行条件下各采样25组数据,总共获得400组数据。滚动轴承故障诊断台的结构图及实物图分别,如图3、图4所示。

图3 滚动轴承故障诊断台结构图Fig.3 Structure Drawing of Rolling Bearing Fault Diagnosis Table

图4 滚动轴承故障诊断台实物图Fig.4 Physical Drawing of Rolling Bearing Fault Diagnosis Table
3.2 基于LMD-SVD特征提取
为了获取故障特征向量,首先应用LMD将原始振动信号分解成多个PF,如图5所示。得到的PF即为原始信号的调频调幅信号,信号包络线为对称的,是一系列具有物理意义的瞬时频率PF分量之和。由LMD-SVD获得的故障特征值部分,如表1所示。从表中可以看出,经过分解后的分量最终可由故障特征向量表示,每个故障特征向量均包括五个数据。

表1 基于LMD-SVD得到的故障特征值Tab.1 Fault Eigenvalues Obtained based on LMD-SVD

图5 基于LMD获得的振动信号PFFig.5 Vibration Signal PF Obtained based on LMD
将基于LMD-SVD所得到的不同状态下的8组故障特征值(奇异值)绘制在同一坐标系下,即得到内圈、外圈和滚动体故障的奇异簇,如图6所示。

图6 内圈故障信号、外圈故障信号和滚动体故障信号奇异值聚类Fig.6 Singular Value Clustering of Inner Ring Fault Signal,Outer Ring Fault Signal and Rolling Body Fault Signal
显然,对于一个特定的故障模式,LMD-SVD得到的奇异值线在不同的运行条件下几乎是一致的。也就是说,奇异值向量即使在变化的条件下也保持高度的一致性。因此,在可变条件下的特征提取方面,LMD-SVD具有显著优势。这些特性保证了在可变条件下应用所提出的特征提取方法的有效性。
在本研究中,滚动轴承的运行状态包括正常、内圈故障、外圈故障和滚动体故障。为了观察不同工作状态下奇异值的可分离性,由LMD-SVD得到的不同工作状态下的奇异值簇,如图7所示。从中我们可以看出,四个工作状态之间的间隙足够大,可以容易地将它们分开。由于奇异值在可变条件下保持了良好的可分离性,因此它们比较适合用作分类器的输入。

图7 不同工作状态下的奇异值聚类Fig.7 Singular Value Clustering under Different Working Conditions
由于本次使用的实验数据来自实验室装置,因此振动信号的噪声水平相对较低,为了验证提出LMD-SVD方法在实际工程中应用的鲁棒性,同时考虑到绝大多数工业应用都可能涉及加性噪声,因此我们进行了LMD-SVD方法能够抵御加性噪声的实验验证。将信噪比分别为0.2、0.4、0.6和0.8的高斯白噪声分别加入到原始振动信号中,将特征提取结果显示,如图8所示。由此可以看出,当信噪比从0.2变化到0.8时,所提取的特征是:当信噪比为0.2时,不同故障状态之间的可分性良好。由于LMD能够自适应地分解任何复杂多分量信号,因此得到期望结果。由于特征在变化条件下具有良好的可分离性,使得分类器易于进行故障诊断,从而得出LMD-SVD方法在一定程度上能够抵抗噪声的结论。

图8 噪声信号的LMD-SVD结果Fig.8 LMD-SVD Results of Noise Signal
3.3 基于极限学习机的故障状态分类
基于LMD-SVD得到的故障特征向量可以用于滚动轴承工作状态识别,而基于ELM的故障状态分类结果部分,如表2所示。即使在可变的条件下,ELM的实际输出也与目标输出极其一致。因此,将LMD-SVD与ELM相结合可以有效地实现变工况下滚动轴承的故障诊断。

表2 基于ELM的状态分类结果Tab.2 State Classification Results based on ELM
由于ELM与SVM相似,因此将ELM与SVM进行对比。显然,ELM比SVM需要更少的人工干预,因为在ELM方法中,只有隐藏层中的神经元数量需要人工确定,而SVM中有两个参数需要在训练之前确定。SVM虽然提供了许多算法来调整两个参数,但是如何选择合适的算法是一个难题,因为它会对整个分类过程产生巨大的影响,特别是在运行时间和分类精度方面。同时,为了比较分类效果,将BP神经网络的一个典型例子应用于分类中。因此,在我们的研究中,比较了ELM、SVM[15]和BP[16]在运行时间和分类精度方面的差异。由于训练样本的数量是分类中的重要影响因素,因此每个操作条件的训练样本数量被设置为10,每个操作状态总共有40个样本。详细的比较结果,如表3所示。其中给出10个例子来计算运行时间和分类精度的平均值以进行比较。

表3 ELM、SVM与BP的分类结果Tab.3 Classification Results of ELM,SVM and BP
BP方法明显比另外两种方法更耗时和更不精确,而且ELM在运行时间和分类精度方面相比SVM仍然具有优势,如图9所示。然而,由于故障特征向量具有良好的可分离性,ELM和SVM之间的差距不是很大,三种方法的分类精度都高于0.9,这进一步验证了所提出方法的有效性。

图9 ELM、SVM和BP在运行时间和分类精度上的比较情况Fig.9 Comparison of ELM,SVM and BP in Terms of Running Time and Classification Accuracy
4 结论
提出了一种基于LMD-SVD和ELM的滚动轴承故障诊断方法,主要贡献如下:(1)采用LMD-SVD方法提取故障特征向量,采用ELM方法对滚动轴承在变工况下的状态进行分类;(2)在滚动轴承特征提取方面,对LMD-SVD方法进行了分析,表明LMD-SVD的优越性在于即使在变化条件下特征向量仍保持较高的重合度;(3)从运行时间和分类精度两方面考虑,将ELM和SVM、BP算法作为故障分类的有效方法进行比较,发现ELM算法耗时少,精度高。
实验结果表明,提出的LMD-SVD和ELM方法适用于变工况下滚动轴承的故障诊断,具有广阔的应用前景。在本研究中,我们仅将此方法应用于滚动轴承,因此今后应在其他旋转机械上进行实验,以验证此方法的通用性或发现推广中存在的问题。
