以MATLAB GUI为平台的代理模型优化设计工具箱
2021-08-28高玉琼吕利叶李建飞宋学官
高玉琼,吕利叶,李建飞,宋学官
(大连理工大学机械工程学院,辽宁 大连 116023)
1 引言
代理模型是一种被广泛应用于工程设计及优化问题中的数学近似方法[1]。在复杂系统的设计空间中,能够以较少样本点为基础拟合出系统输入参数和输出值之间的关系,具有拟合精度好、成本低、工作效率高等特点。常用的代理模型技术包括多项式拟合曲面(Polynomial Regression Surface,PRS)[2]、径向基函数(Radial Basis Function,RBF)[3]、克里金(Kriging,KRG)[4]等,基于代理模型技术的优化设计流程一般,如图1所示。i SIGHT和MATLAB具有强大的计算及优化能力,但操作门槛较高,对于用户的专业知识能力和计算机的硬件水平要求较高。借助可视化工具GUI可以降低代理模型技术的使用难度,在解决问题的过程中为用户提供现有任务和解决方案之间的用户行为交互及数据传输,用户在界面上的操作结果可以被展现在MATLAB的图形窗口中[5]基于MATLAB的用户图形界面工具开发应用十分广泛:文献[6]开发出基于MATLAB GUI的图像处理平台,文献[7]设计出全局敏感度分析工具箱,文献[8]开发出数据驱动的相似分类法(SIMCA)用户界面。
提出了一种基于MALTAB用户图形界面的代理模型优化设计工具箱,该工具箱主要包含试验设计、建立代理模型、预测及优化三个模块。通过数值分析实例证明该工具箱的实用性,能够很好的帮助用户解决常见工程设计优化问题,同时也能够推广代理模型技术的应用。
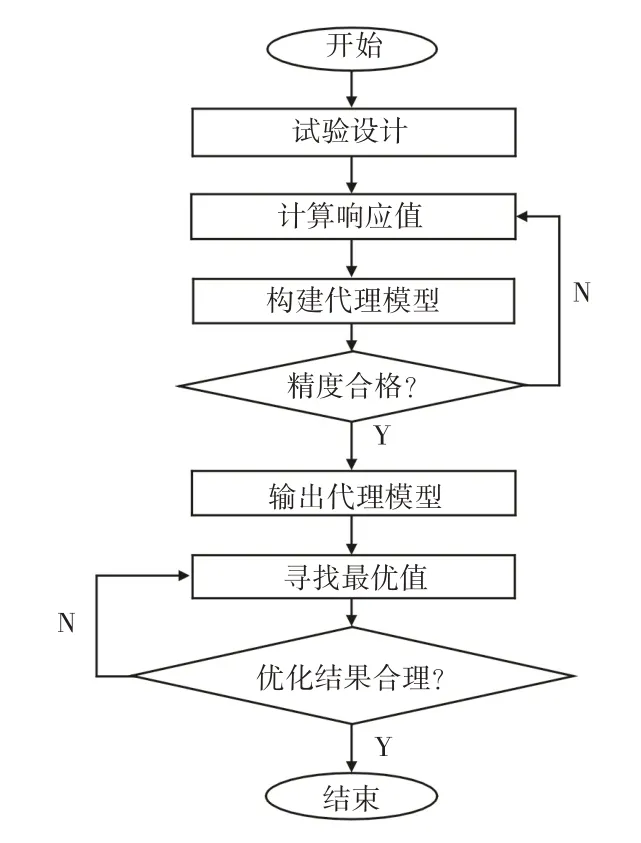
图1基于代理模型的设计及优化流程图Fig.1 The Flow Chart of Surrogate-Based Design and Optimization
2界面框架
SBDO工具箱包含四个模块。用户打开主界面后,依据窗口提示首先打开试验设计窗口进行随机抽样取点。该界面囊括了四种常用抽样方法,分别是拉丁超立方试验设计(Latin Hyper⁃cube Design,LHD)、全析因试验设计(Full-factorial Design,FFD)、Box-Behnken试验设计(Box-Behnken Design,BBD)和中心复合试验设计(Central Composite Design,CCD)。用户只需要按提示在界面输入框中输入自变量的数目和取值范围,便可以选择任意一种抽样方法对自变量进行取点,由于代理模型的建立和精度检测需要训练点及检测点,用户需要进行两次抽样,抽样结果通过保存按钮保存在DOE_Points.xlsx表格中,相应的响应值需要用户通过仿真计算得到。
完成抽样取点后关闭DoE界面,可在主界面上按提示点击按钮打开建立代理模型窗口。该界面包含三种常用的代理模型理论,分别为PRS、RBF和KRG。用户导入训练点和测试点信息后,通过切换代理模型方法,便可以建立代理模型并检测其精度,检测指标的计算结果将会以数值方式显示。界面还包含有基于期望的加点方法,若模型精度为达到要求,用户可更换代理模型类型、重新抽样或通过添加训练点来增加模型拟合精度。
完成上述工作后,最后打开预测及优化窗口,在该界面中用户可通过优化算法找到最优解,待优化问题的目标函数既可以是通过上一步建立的代理模型拟合值,也可以是用户自定义函数。此界面包含常用的遗传算法(Genetic Algorithm,GA)、多目标遗传算法(Multi-Objective Genetic Algorithm)和粒子群算法(Parti⁃cle Swarm Optimization,PSO)等。各模块的结果将会以数值或图形显示在用户界面中,SBDO工具箱的框架图,每一个模块都包含了若干理论方法,如图2所示。

图2 SBDO工具箱的框架图Fig.2 The System Block Diagram of SBDO Toolbox
2.1试验设计模块
抽样通常是基于代理模型的设计及优化方法的第一步,是一种用计算机模拟实验取样过程的数理统计方法,在试验设计模块中能够随机生成建立代理模型所需要的训练点和检测点。为了使代理模型更加贴近真实的变量和响应值之间的关系,样本点应随机分布并尽量布满设计空间。该模块主要包含四种试验设计方法,其中LHD常用于自变量多维分布的设计空间,它能快速生成大量近似随机分布的样本点[9],是一种应用广泛的抽样方法;FFD是一种多因素交叉分组设计方法,所得到的样本点与真实抽样实验结果相同,展现出每个变量的所具有的全部水平组合方式,得到的样本点信息量较多;BBD常适用于响应面分析,它是一类基于三层不完全因子设计的可旋转或近似可旋转二阶设计,适合自变量因素(维度)较少时使用。CCD是二阶二次型设计方法,与BBD的适用范围类似,但在相同因素下的实验次数比BBD更多。
2.2代理模型构建模块
该模块旨在引导用户通过界面操作,建立一个代理模型以近似模拟自变量与目标函数之间的关系并检验模型精度,界面中还提供了一种加点准则以增强模型的拟合精度。该模块主要包含三种典型代理模、精度检验和加点策略。
2.2.1多项式响应曲面代理模型
多项式响应曲面代理模型也被称作为多项式回归分析,是一种基于最小二乘法的回归分析方法,拟合结果具有良好的连续性和可导性,能较好的去除数字噪声的影响,易于后续寻找最优解。对于n维变量,它的多项式公式基本形式为:


2.2.2径向基函数代理模型
径向基函数是一种用于离散多变量数据的插值拟合方法,它的计算速度较快,拟合精度及鲁棒性较好。其响应值可以看作各种径向基函数的线性组合,基本数学表达式为:

在建立代理模型的过程中,为了得到唯一解,径向基函数中的矩阵应为方阵,因此指定径向基函数代理模型基本公式可以表示为ΨW=Y,W的计算公式为W=Ψ-1Y。常用的径向基函数有线性函数,立方型函数,高斯函数,多重二次曲面函数,倒多重二次曲面函数等类型。
2.2.3 Kriging代理模型
Kriging模型是一种估计方差最小的无偏估计模型,是基于高斯过程的内插拟合方法,在处理局部数据突变的问题时拟合精度较高,可以较好的处理各类各向同性或各向异性问题,但它的数学公式较为复杂,建立代理模型时的计算工作量较大。Kriging代理模型的基本数学公式为:

式中:f(x)—已知的近似模拟模型;z(x)—高斯随机过程。
高斯过程的期望为0,协方差矩阵为:

式中:σ2—z(x)的方差;R—相关系数矩阵相关函数,最常用的是高斯函数。
则基于Kriging的最佳预测估计响应值计算式为:

式中:f—由n个样本点的输出值组成的列向量;r—未知点x与样本点之间的相关向量。

方差的最大似然估计(Maximum Likelihood Estimates,MLEs)为:

高斯函数中的未知参数θ的计算公式为:

2.3预测及优化模块
在本模块中,用户可选择优化算法在整个设计及优化空间中寻找最优解决方案。该模块内置2种优化算法用于解决无约束最小值问题,1种优化算法用于解决带约束的非线性规划问题,以及遗传算法GA、多目标遗传算法和粒子群算法PSO。GA是一种基于自然选择和生物进化的寻优算法,在寻优过程中,通过模拟自然生物界的选择、交叉和变异过程找到最优解;多目标遗传算法可以针对多个目标值得到Pareto最优解;PSO是一种从随机初始值开始,通过迭代来搜寻最优解的进化算法。对于算法中的目标函数,用户既可选择使用在上一步中建立的代理模型进行预测,也可以自定义目标函数数学关系式。在搜寻最优解的过程中,全局敏感度分析结果也将以表格形式展现在本模块界面上,它体现了各个变量对于输出值的影响程度。
3用户界面设计及显示效果
基于上述的理论及系统框架,接下来就可以借助MALAB GUI来设计并完成用户界面的搭建和应用。首先根据用户的操作习惯和界面功能设计出界面的理论框架布局,随后在GUIDE中设计好控件分布和排列,最终在MATLAB编辑器中编写功能函数、数据传递、控件补完、逻辑调配和错误警示等功能。完成上述工作后可以开始运行程序并验证SBDO工具箱的实用性。经过测试后的SBDO工具箱可用于工程实践。在开发SBDO工具箱的过程中,最主要的工作是对于用户界面的设计和代码编写。为了更好的用户体验,工具箱的界面设计严格遵循简单性、一致性、习常性的原则。各模块的显示窗口被分为多个区域展现输入、设置项切换、结果显示等功能。在用户操作的过程中会检测用户输入项是否完整、格式是否正确而及时弹出警示框,数据能够及时存档,不会因突发异常而丢失,具有很好的连续性和用户体验。
工具箱主界面包含软件的图标、三大模块按钮和最终结果显示框等内容,如图3所示。用户可按照提示依次点击试验设计、建立代理模型、优化等按钮来打开各模块的窗口并得到相应的结果,未操作过的面板底色为灰色,操作过的面板为白色。最终的设计及优化结果也将呈现在主界面下方的文字框中。

图3 SBDO工具箱主界面框架设计及窗口显示Fig.3 The Frame Design and Display of SBDO Toolbox’s Main Window
试验设计模块的用户界面包含多个显示和功能区域,如图4所示。

图4试验设计模块的框架设计和窗口显示Fig.4 The Frame Design and Display of DOE Module Window
用户可在左上角选择抽样方法,输入自变量的维度和取值范围,在右侧切换抽样方法的设置项后点击相应按钮,则样本点数据将会展现在右下角的表格中,用户可点击画图选择查看各样本点在空间分布的情况。在该界面中,抽样方法的选项均有默认值,若用户无需选择其他选项,保持默认状态即可。样本点产生后,用户可选择将样本点保存到excel表格,或默认在空间中保存为mat文件,以便于根据样本点仿真计算得到对应的响应值。在该模块中,用户可以以少量简单操作完成抽样并直观查看抽样结果。
建立代理模型模块的理论框架和最终展示效果,如图5所示。窗口主要分为两个区域:模型选项及显示区域、模型数据操作区域。用户可在左上角的弹出式菜单中选择需要建立的代理模型的类型并设置相应的选项。建立和检测代理模型所需的训练点和测试点可以直接采用上一步的DoE结果,也可以从excel表格中导入,显示在右下角的表格中。模型的精度检测结果将会显示在右下角的表格中,用户也可以在右上角选择变量来查看代理模型的插值拟合图形。若模型检测结果精度不足,可以点击加点按钮进行加点重新建立代理模型并检测精度。本模块中的PRS、RBF和KRG代理模型源代码来源于Felipe A.C.Viana[10]。
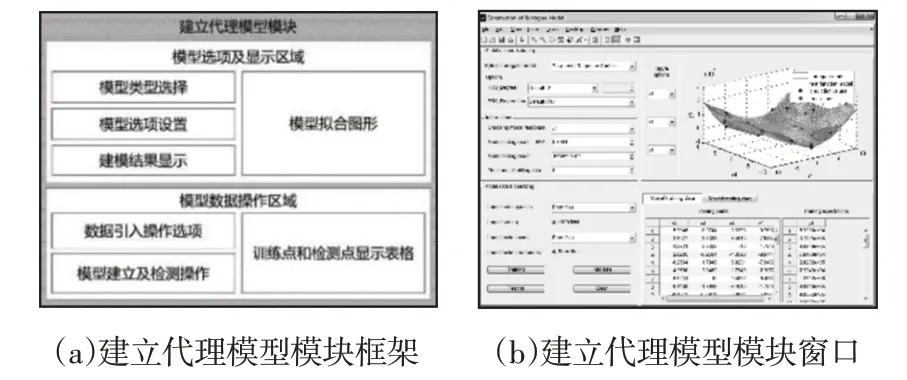
图5 建立模型模块的框架设计和窗口显示Fig.5 The Frame Design and Display of Construction of Surrogate Model Module
预测及优化模块的用户界面,如图6所示。在该模块中,用户可根据选择不同的优化算法,提示输入优化问题中自变量和约束等相关信息,优化过程中的目标函数可以选择由上一步建立的代理模型根据最优解近似预测,也可以自行定义函数或数学关系式。最终的优化结果将会显示在左下角的白色文本框中,全局敏感度分析结果则以表格形式展现。右侧的优化算法参数设置项在不同的算法时也不一样,用户可根据实际情况进行切换调整或保持默认状态。在进行设计和优化过程中,用户操作不当或输入参数不完整时将会及时弹出错误警示框进行提示。

图6 预测及优化模块的框架设计和窗口显示Fig.6 The Frame Design and Display of Prediction∕Optimization Module Window
4 数值算例分析
为了验证SBDO工具箱的实用性,本章将利用SBDO工具箱完成一系列数值算例,用于测试工具箱的功能、用户体验和展示效果。在进行数值算例验证的过程中,按照基于代理模型的工程设计及优化流程,首先在试验设计模块进行抽样得到若干训练点和检测点信息,随后在建立代理模型模块建立代理模型并检测模型精度,最后在预测及优化模块利用优化算法寻找最优解。考虑到不同代理模型的原理和拟合效果不同,单一测试函数的结果并不具有代表性,因此本次采用25组不同特性的测试函数进行检测。这些函数既有非线性也有线性,自变量维度在(2~16)之间。样本点对应的真实响应值由测试函数求得,预测值则分别由PRS、RBF、KRG三种代理模型求得,以此看出各代理模型的拟合精度,RMSE的值,如表1所示。r2的值,如图7所示。值得一提的是,检测结果与代理模型技术本身的特点有关,SBDO工具箱意在为用户提供简单实用的代理模型技术的工具,而不能更改代理模型的拟合结果。

表1 25个测试函数在三种代理模型中的RMSE值Tab.1 RMSE of Three Surrogate Models in 25 Test Functions
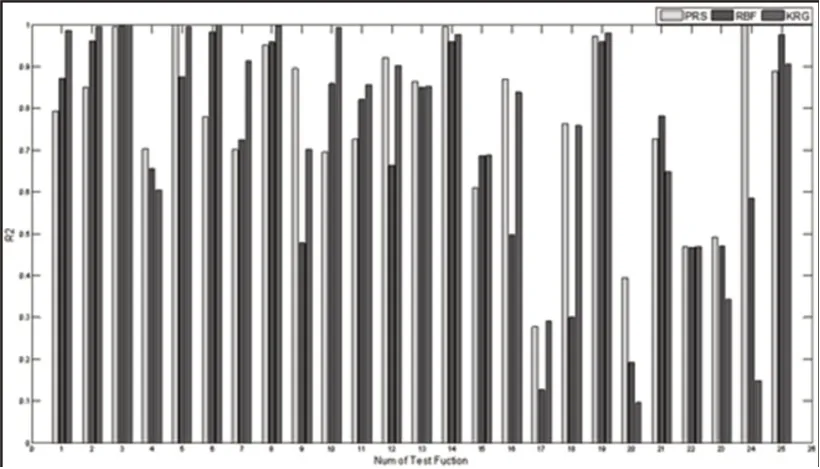
图7 SBDO工具箱中三种代理模型的r2值Fig.7 r2 of Three Surrogate Models in SBDO Toolbox
通过数值算例的操作及结果展示,SBDO工具箱可以完成简单的工程设计及优化的全部过程。对同一个测试函数,不同代理模型的拟合精度不同,而不同性质的测试函数则体现了代理模型广阔的应用范围和优缺点。通过SBDO工具箱,用户可以通过输入变量信息、切换选项设置、点击按钮等操作得到建模和优化的结果。若建立的代理模型精度不符合要求,用户可以通过加点操作、切换代理模型类型或重新抽样取点等操作取得改善。
5 结论
主要提出了一种基于代理模型的设计及优化MATLAB工具箱SBDO,主要通过试验设计、建立代理模型、预测及优化界面引导普通用户解决常见工程设计及优化问题。该系统具有很强的实用性、交互性和开放性。用户的操作门槛低,且不需要掌握专业的机械结构、优化算法、编程等专业知识即可使用,有助于推广代理模型理论的使用范围。
在今后的工作过程中,SBDO工具箱将被应用于实际工程设计优化问题,并将在不断的实践和反馈过程中进行改善和升级。目前工具箱中所包含的理论方法还不够多,界面设计仍有完善空间。我们期待为用户提供一个方法更加多元、界面更加美观、使用更加方便的基于代理模型的工程设计及优化工具箱。
