非相干噪声减载的空域加窗解卷波束形成
2021-08-28王昊马启明
王昊,马启明
(杭州应用声学研究所 声纳技术重点实验室,浙江 杭州 310012)
0 引言
在实际声纳系统中,由于常规波束形成器(CBF)具有稳健性高、运算量小的优势,相对于自适应类算法[1-3]、子空间类算法[4-5]、稀疏约束类算法[6-9]具有更多的应用空间。但是,实际中受物理孔径、信噪比等的影响,CBF空间分辨率低、弱目标检测能力差。同时,在声纳的实际使用环境中存在众多强干扰,其空域旁瓣泄漏会导致波束形成器对弱目标的检测性能严重下降。传统处理方法是采用空域加窗,以压制波束的旁瓣、抑制干扰的空域泄漏。但是,加窗处理展宽了波束主瓣,进一步降低了波束形成器的多目标分辨能力。文献[10-11]将图像处理中常用的解卷处理引入空间谱估计中,利用CBF的卷积特性,对波束形成输出的空间能量谱解卷积,在理想条件下可以得到类似delta函数的目标空间功率分布,抑制了干扰的旁瓣泄漏,提高了波束分辨率。但是,其处理建立在均匀加权波束形成器输出的基础上,在干扰过强、旁瓣泄漏能量级高的情况下,弱目标淹没其中,单纯地增大迭代次数依然无法解卷出弱目标信号。
另一方面,解卷仅解决了强干扰旁瓣泄漏的问题,未考虑噪声的影响,在低输入信噪比条件下,特别是在各阵元噪声功率不一致时,解卷对弱目标的检测性能下降。文献[12]建立了最优化问题,对协方差矩阵对角线上的非相干噪声功率进行估计,以缓解噪声的影响,但是在快拍数不足(快拍数小于阵元数)时,对噪声功率估计误差增大,性能下降[13]。
针对上述问题,本文提出一种非相干噪声减载的空域加窗解卷波束形成算法。首先,求解半定规划问题,对阵元非相干噪声功率进行估计、分条件讨论,在快拍数小于阵元数时,对比协方差矩阵的特征值与噪声估计值,对特征值修正,减载噪声;在快拍数大于等于阵元数时,以半定规划问题的解对协方差矩阵对角线元素减载,如此提高了入射信号的输入信噪比。然后,提出基于加窗波束形成器的平移不变性,利用解卷技术对空域加窗波束形成器的输出解卷,以缓解空间中强干扰的旁瓣泄漏。由于进行了非相干噪声减载同时加窗空间谱解卷处理,在抑制空域干扰泄漏的同时,降低了背景噪声级,提高了波束形成器对空间中弱目标的检测性能。
1 信号模型
假设空间中J个相互独立的信号分别从θj(j=1,2,…,M)方向入射到阵元数为M的均匀线列阵,阵元间距为D,以首阵元为坐标原点、x负半轴为0°,顺时针扫描180°,则阵元接收信号第k个快拍的模型可以表示为
(1)
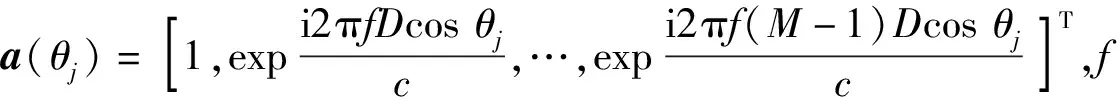
将(1)式表示为向量形式,
X(k)=A(θ)S(k)+N(k),
(2)
式中:A(θ)=[a(θ1),a(θ2),…,a(θJ)];S(k)=[s1(k),s2(k),…,sJ(k)]T。
当阵元间噪声互不相干时,理论协方差矩阵为
(3)
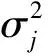
实际中难以得到理论协方差矩阵,以有限快拍对其进行估计,K个快拍的估计可表示为
(4)
2 非相干噪声减载的空域加窗解卷波束形成
2.1 非相干噪声功率估计
对于阵元非相干噪声,本节在波束形成前噪声减载,以此消除非相干噪声对后续解卷处理的影响。
文献[12]建立了半定规划,通过求解最优化问题估计阵元非相干噪声功率,再对角线减载以消除其影响,最优化准则可表示为
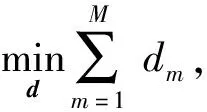
s.t.+diag(d)≥0,
(5)
式中:d表示非相干噪声估计。
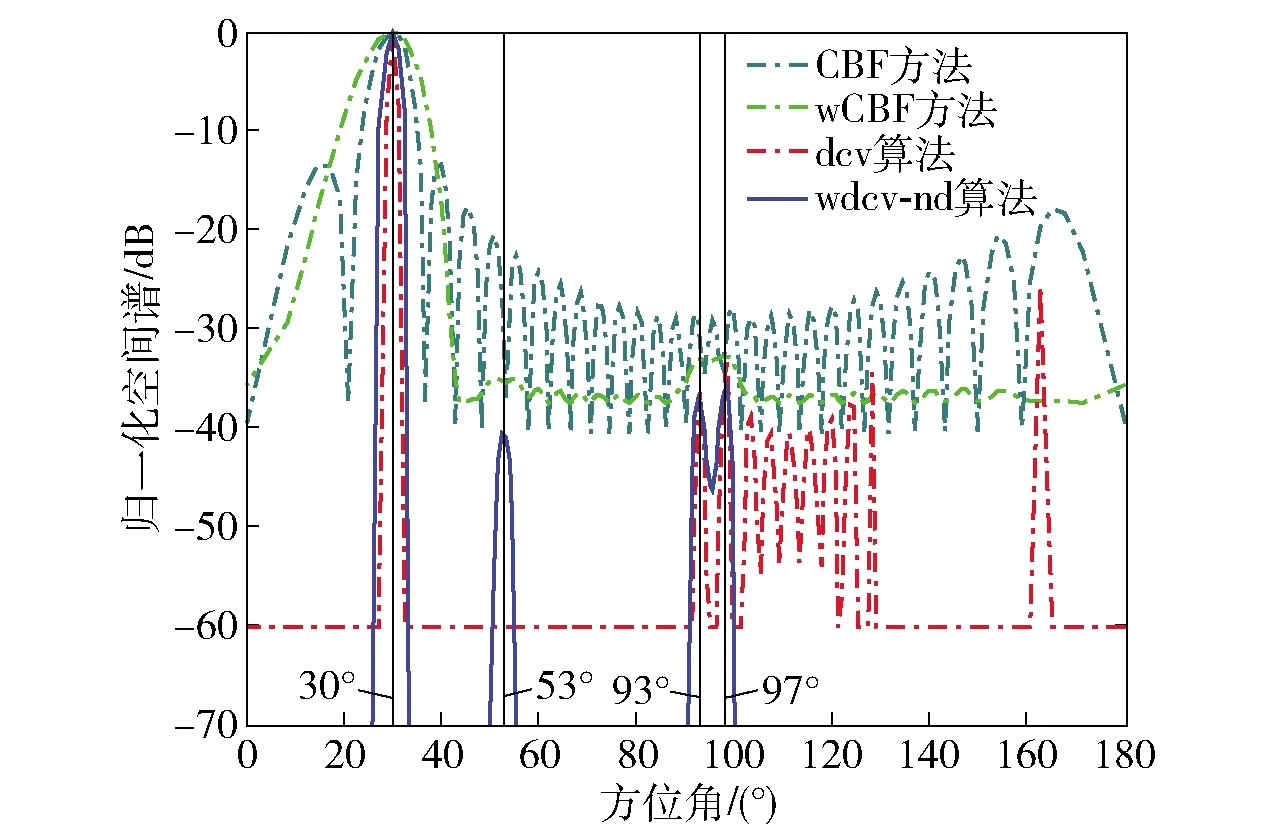
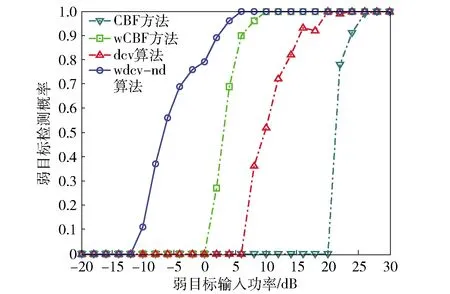
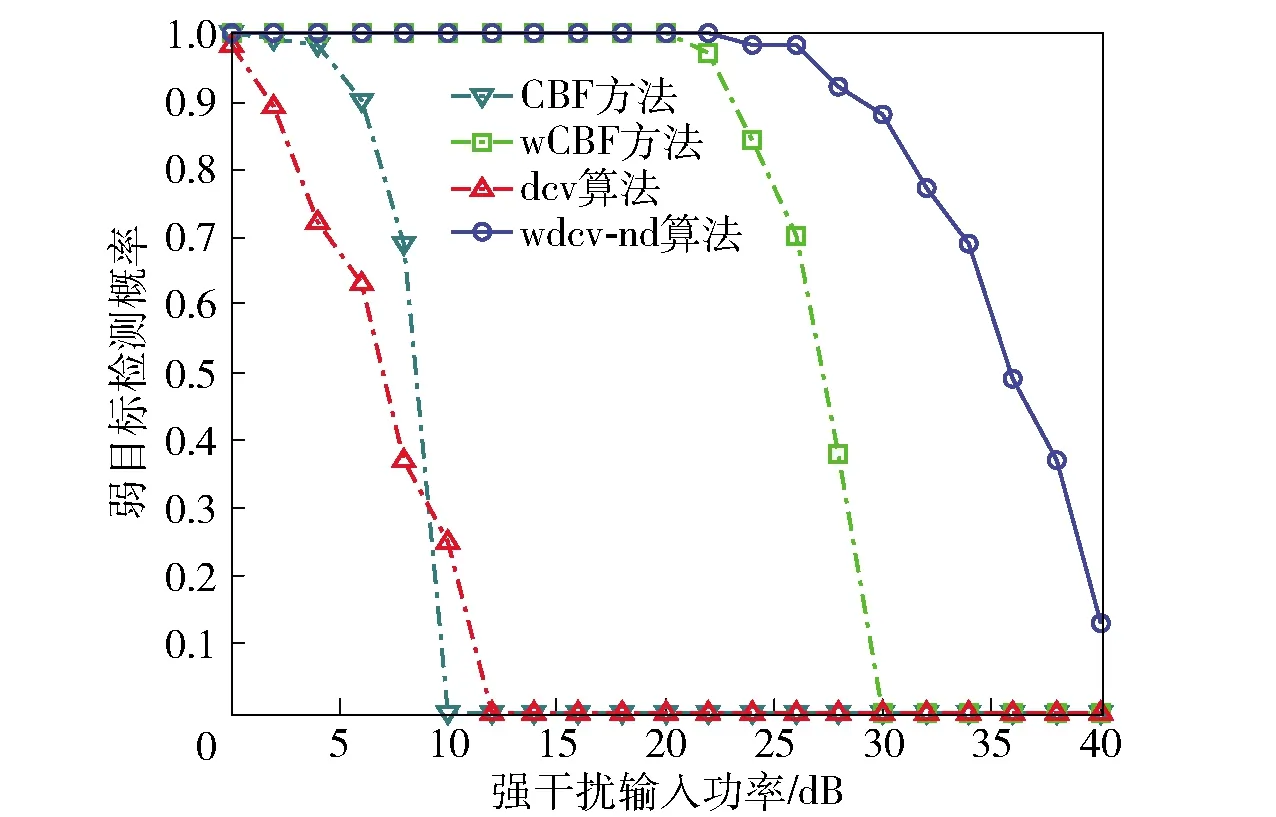
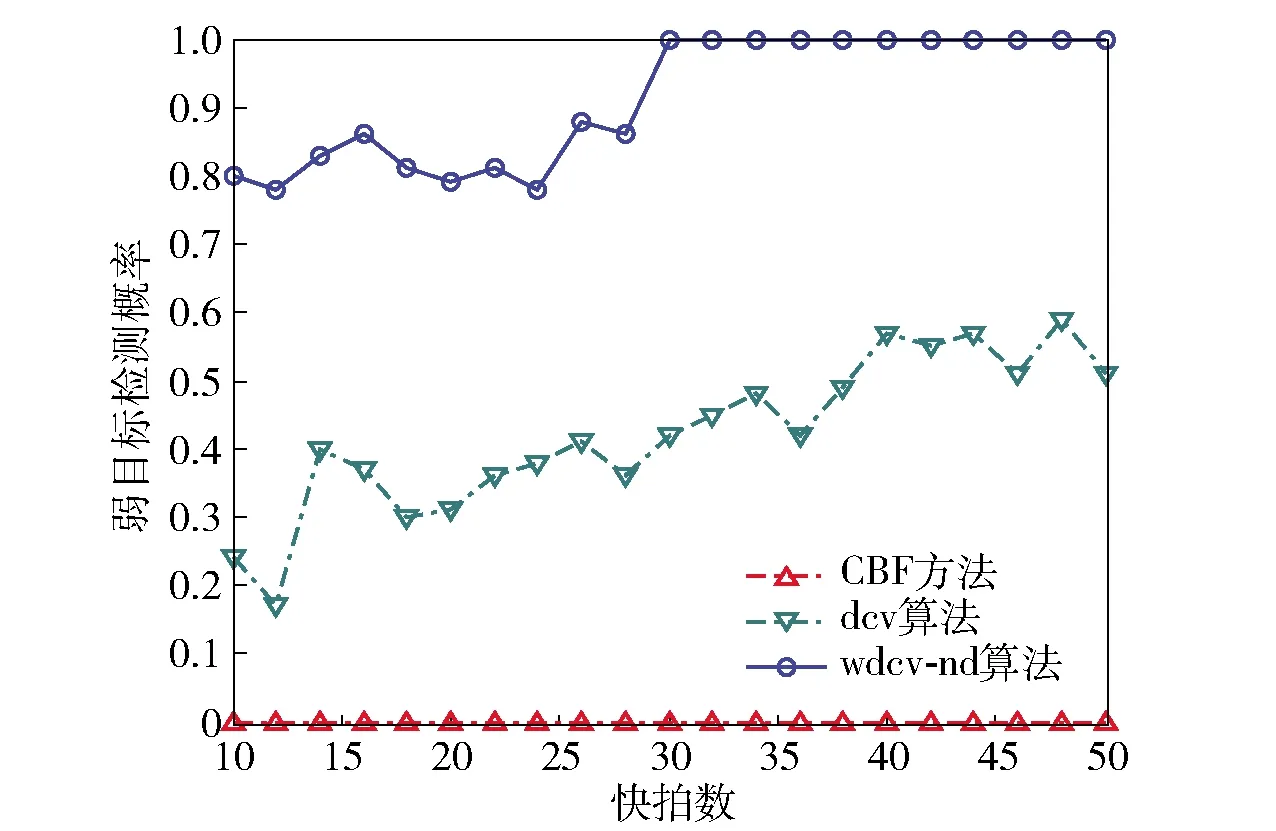
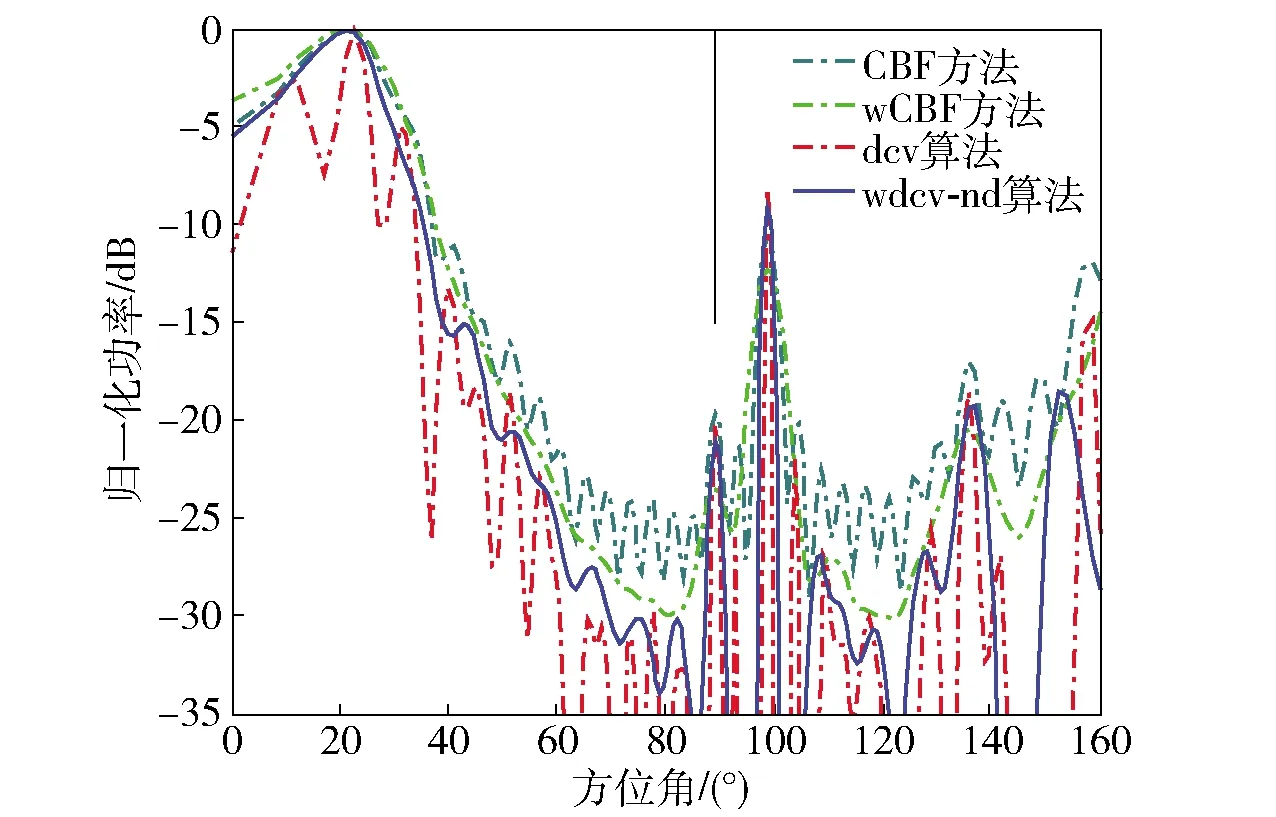
上述约束在快拍数大于阵元数(K≥M)时有效,当快拍数小于阵元数(K (6) 式中:λm表示采样协方差矩阵按大小升序排列的特征值,em表示对应的特征向量。通过(7)式估计噪声功率λn(n=1,…,M), s.t.λn>min(|d|), (7) 进而修正特征值为λ′m, (8) 由此可得本文噪声减载后的协方差矩阵: (9) 文献[10]提出对CBF的输出解卷处理,部分缓解了旁瓣泄漏的问题,提高了波束形成器的空间分辨率。但是,当空间中干扰能量过强时,传统波束形成器的旁瓣泄漏严重,弱目标的波束输出远远小于强干扰的旁瓣级,此时简单地提高迭代次数亦无法解卷出弱目标的能量。本文基于空域加窗处理的旁瓣抑制优势,结合解卷的波束分辨率优势,得到一种空域加窗解卷算法。利用空域加窗的波束图构造点扩展函数,再对空域加窗波束形成的输出解卷处理,得到本文算法的空间谱,以此获得良好的弱目标检测能力。 首先,采用空域加窗的波束形成器获得空间能量谱估计: (10) 式中:PwCBF(cosθ)为噪声减载的加窗波束形成(wCBF)的输出;ωw(cosθ)为权向量, ωw(cosθ)=wind⊙a(cosθ), (11) wind表示与角度θ无关的窗函数向量,⊙表示向量点乘。 非相干噪声减载后,忽略噪声的功率输出,常规波束形成的输出可以表示为卷积形式: PwCBF(cosθ)= (12) 空间中目标的真实能量分布情况如(13)式: (13) 式中:|Aj|2为信号功率;δ(·)为单位冲击函数。 从而可以基于空域加窗的波束图,通过R-L迭代算法[14-15]解卷出目标的能量分布状况: (cos ϑ)i+1= (14) 3.1.1 利用仿真实验验证所提算法的性能 空间中4个相互独立的信号入射到半波长布阵的均匀线列阵声纳,信号在不同时间批次服从高斯分布,频率500 Hz,阵元间距1.5 m,阵元数30,声速1 500 m/s,信号入射角度分别为[30°,53°,93°,98°],对应的阵元域输入功率分别为[35 dB,-5 dB,0 dB,0 dB],考察其对53°弱目标的检测能力以及对93°、98°等功率目标的分辨能力。阵元噪声相互独立,功率不完全一致,分别为[15 dB,14 dB,13 dB,12 dB,11 dB,10 dB,9 dB,8 dB,7 dB,6 dB,5 dB,4 dB,3 dB,2 dB,1dB,1 dB,2 dB,3 dB,4 dB,5 dB,6 dB,7 dB,8 dB,9 dB,10 dB,11 dB,12 dB,13 dB,14 dB,15 dB],空间扫描间隔按等余弦划分,共180个波束,积分时间60批,对于本文算法,空间窗采用hamming窗处理,其他窗函数类似。采用cvx凸优化工具箱进行减载噪声功率估计(或采用迭代正则化方法进行求解[16]),解卷处理均迭代20次,分别得到CBF方法、wCBF方法、文献[8]解卷积(dcv)算法以及本文wdcv-nd算法的归一化空间谱,如图1所示,其中目标的真实方位如图1中竖线所示。 图1 4种方法的归一化功率谱 由图1可以看出,受30°强干扰旁瓣泄漏的影响,CBF方法无法检测出53°的弱目标,在其方向上存在干扰导致的零陷,同时无法对93°和98°的两个等强目标分辨。wCBF方法虽然降低了旁瓣级,但是由于干扰过强,其53°谱峰出现了分叉,同时无法分辨93°和98°两个等强目标。传统dcv算法锐化了30°干扰的波束宽度、降低了旁瓣级水平,但是由于干扰能量过强、旁瓣泄漏严重,无法解卷出53°的弱目标,同时由于旁瓣级高,解卷后甚至产生了伪峰,93°和98°的等强目标混杂于解卷后的旁瓣中,无法准确辨别。对于本文所提wdcv-nd算法,由于采用了非相干噪声减载,降低了背景噪声对波束形成器的影响,由此空间谱具有更低的背景级。同时,空域加窗再解卷处理,既获得了加窗处理的低旁瓣,又具有解卷处理的波束分辨优势,改善了加窗波束形成器空间分辨率下降的问题,在有效抑制30°强干扰的旁瓣泄漏、检测出53°弱目标的同时,成功分辨了93°和98°两个等强目标。由此可知,本文所提算法比传统解卷方法具有更好的强干扰及噪声抑制能力。 3.1.2 通过独立重复试验验证算法在强干扰影响下对弱目标的检测概率 首先,固定强干扰的输入功率,调整53°目标的输入功率以2 dB的步长从-20 dB变化到30 dB,其他仿真条件不变,每种输入功率条件下进行100次独立重复实验,统计不同方法或算法对弱目标的检测概率,如图2所示。 图2 检测概率随弱目标功率变化曲线 由图2可以看出,随着弱目标输入功率的增加,4种方法或算法对弱目标的检测概率均变大。同时,在不同输入功率条件下,本文算法的检测概率均优于CBF方法和传统dcv算法,信号检测阈值最低。 令53°目标的输入功率固定为-5 dB,调整30°强干扰的输入功率以2 dB为步长从0 dB变化到40 dB,其他仿真条件不变,每种输入功率条件下进行100次独立重复实验,统计不同方法或算法对弱目标的检测概率,如图3所示。 图3 检测概率随强干扰功率变化曲线 由图3可见,随着强干扰输入功率的增加,其旁瓣泄漏逐渐严重,4种方法对弱目标的检测概率均变小。在干扰输入功率小于10 dB时,强干扰的旁瓣泄漏、阵元噪声远强于53°目标,dcv算法的解卷误差增大,目标方位估计精度降低,对弱目标的检测概率甚至低于CBF方法。在不同输入功率条件下,本文算法均具有最优的检测概率。 3.3.3 仿真验证所提算法在不同快拍数条件下的性能 令53°期望目标的输入功率为10 dB,快拍数以2为步长从10变化到60,每种快拍数条件下进行100次独立重复实验,统计不同快拍数条件下不同方法对目标的检测概率,如图4所示。 图4 检测概率随快拍数变化曲线 对于CBF方法,单纯地增加快拍数不能消除强干扰旁瓣泄漏的影响,故此随着快拍数的增加,始终无法对53°目标检测。随着快拍数增加,部分缓解了噪声对解卷处理的影响,以此随着快拍数的增加,dcv算法对53°目标的检测概率增大。本文所提wdcv-nd算法由于采取了非相干噪声减载,消弱了噪声对解卷的影响,同时由于采用空域加窗的解卷处理,有效抑制了强干扰的旁瓣泄漏影响,如此具有最优的检测性能,随着快拍数的增加,对噪声的减载效果越好,故而对53°目标的检测概率逐渐增大。 采用阵元数为30、以500 Hz对应半波长布阵的拖线阵声纳数据,空间扫描波束以等余弦方式划分,共180个波束,积分时间为60T(T为单批数据时间长度,T=0.8 s),空间窗采用Hamming窗,解卷处理均迭代20次,得到某一时刻4种方法的空间能量谱,如图5所示。 图5 海试数据处理某一时刻切片图 图5中,20°附近的强干扰是本船噪声,竖线指示的方位为合作声源经GPS折算后的实际方位,可以看出其近旁99°存在一强干扰。对于CBF方法而言,目标波束附近存在强旁瓣泄漏。wCBF方法展宽了波束主瓣,降低了空间分辨率。dcv算法降低了旁瓣级。但是,由于强干扰的输入干噪比过强,dcv算法的旁瓣依然多而丰富,如同CBF方法的处理结果,合作目标混杂于旁瓣当中,难于甄别。本文所提算法由于采用空域窗处理抑制了强干扰的旁瓣泄漏,同时进行了非相干噪声减载,缓解了噪声的影响,避免了过多的伪峰出现,有效检测出了目标。 CBF方法、wCBF方法、dcv算法和本文所提wdcv-nd算法的方位历程图如图6所示。由图6可以看出:对于CBF方法,合作目标淹没于99°的旁瓣泄漏当中,无法判别;wCBF方法展宽了波束,合作目标与干扰难以分辨;对于dcv算法,强干扰的旁瓣依然多而繁杂,合作目标的历程混杂在众多旁瓣中,难以分辨;而本文算法在牺牲部分dcv算法波束分辨率的条件下,压低了强干扰的旁瓣级,得到了清晰、持续的目标方位历程。 图6 4种方法的方位历程图 本文提出一种空域加窗的解卷处理方法,在空间中存在强干扰泄漏时能够有效抑制其旁瓣泄漏,提高解卷处理的弱目标检测能力。同时,将噪声减载技术引入解卷处理之前,以此降低非相干噪声对解卷处理的误差影响。仿真及海试数据处理表明,本文所提算法能够有效改善解卷处理在强干扰及非相干噪声影响下的性能,提高其检测能力。 应当指出,实际中受有限采样快拍的影响,各阵元间噪声不可能完全独立,此时相关噪声成分会影响最优化解出的噪声量,从而影响噪声减载的性能,下一步有必要针对此问题开展相关研究。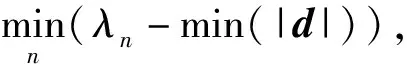
2.2 空域加窗解卷
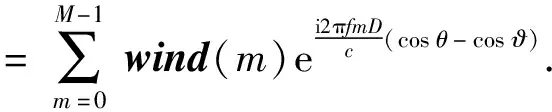
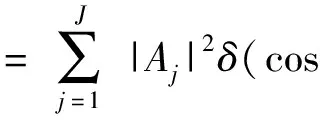
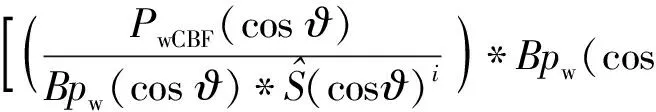
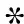
3 仿真实验及海试试验
3.1 仿真实验
3.2 海试数据

4 结论
