2,4-二硝基苯甲醚基熔铸含铝炸药圆筒试验及爆轰产物状态方程

李淑睿，段卓平，郑保辉，罗观，黄风雷

(1.北京理工大学 爆炸科学与技术国家重点实验室, 北京 100081; 2.中国工程物理研究院 化工材料研究所, 四川 绵阳 621999)

0 引言

近年来，随着不敏感弹药系统研究的开展，钝感炸药作为不敏感弹药安全性的核心，也成为相关领域的研究重点。含铝炸药因具有能量密度高、感度低、易于装填等特点，已在不敏感弹药中广泛应用，作为评估弹药装药在意外冲击刺激下感度和安全性的关键，含铝炸药的冲击起爆特性研究成为炸药爆轰领域密切关注的热点[1-4]。炸药冲击起爆反应流场的描述涉及到炸药化学反应进程、未反应炸药压缩状态、爆轰产物膨胀过程等多个部分，其中爆轰产物的膨胀过程以及产物系统各状态参量之间的关系由爆轰产物状态方程描述，因此炸药产物状态方程及参数的合理确定对于炸药冲击起爆特性的准确描述具有重要意义[5]。

含铝炸药中的铝粉主要在爆轰波阵面反应区后与爆轰产物气体发生二次反应，放出大量热量，从而提高炸药的爆热和做功能力，且铝粉燃烧反应的时间尺度较长，因此含铝炸药爆轰产物的膨胀过程是非等熵的[6-8]。而在冲击起爆过程中，由于炸药内部的压力、温度、反应程度等均低于爆轰反应区，可将铝粉视为不发生化学反应的惰性物质，则其爆轰产物仅为主体炸药反应产生的爆轰产物，且产物的膨胀过程是个等熵过程[9]。若直接采用含铝炸药的产物状态方程及参数描述其冲击起爆过程，会夸大铝粉在冲击起爆阶段的反应量，使得产物气体压力、温度、内能等状态参量的描述出现较大偏差，从而影响含铝炸药冲击起爆过程的准确描述。因此关于准确描述含铝炸药冲击起爆过程中爆轰产物状态的研究亟待开展，以支撑含铝炸药的冲击起爆反应流计算以及不敏感弹药的冲击安全性评估。

圆筒试验是评估炸药爆轰产物驱动做功能力的标准方法之一，试验获得的炸药爆轰产物作用下金属圆筒壁的径向膨胀历程，可用于评价炸药爆轰产物的做功能力，以及确定炸药的爆轰产物状态方程参数[10-14]。圆筒试验主要采用高速扫描相机记录不同时刻圆筒壁的位置，从而得到圆筒壁径向膨胀距离随时间的变化历程，但该方法存在圆筒壁膨胀起始点难以准确判读的缺点，同时在炸药爆轰驱动的初期阶段，通过拟合求导获得的圆筒膨胀速度历程存在一定的失真和信息缺失的情况[10,12]。近年来快速发展的激光干涉测速技术，因具有响应速度快、测试精度高等优点，目前已被广泛应用于各类爆炸冲击测试[15-18]，由于其在炸药圆筒试验中可直接精确测得包括爆轰驱动初期阶段细节在内的金属圆筒膨胀速度，克服了高速扫描相机方法存在的缺点，因此逐渐成为圆筒试验的主要测试技术[14,19-20]。

本文基于光子多普勒速度(PDV)测试技术，建立φ50 mm标准圆筒试验测试系统，对2,4-二硝基苯甲醚(DNAN)基熔铸含铝炸药RA1(奥克托今(HMX)/DNAN/铝粉)和含氟化锂(LiF)炸药RF1(HMX/DNAN/LiF)进行圆筒试验测试，利用试验结果分别确定RA1和RF1炸药的爆速及其爆轰产物状态方程参数，进而明确含铝炸药冲击起爆过程中爆轰产物状态方程参数的确定方法。

1 圆筒试验设计

在含铝炸药爆轰反应研究中，由于铝粉的燃烧反应过程不能被直接观测，为了明确含铝炸药的爆轰反应机理，通常采用惰性物质LiF代替含铝炸药中的铝粉。因为LiF的密度、冲击阻抗、分子质量等物理性质与铝粉接近，同时化学性质较稳定，不会与炸药产物气体发生反应，因此通过含铝炸药和对应含LiF炸药研究结果的对比，可探究爆轰反应过程中铝粉的反应历程和机理[14,21]。由于含铝炸药冲击起爆过程中铝粉的反应量极少可忽略，其爆轰产物可假设仅为主体炸药组分反应产生的产物，因此本文也采用LiF代替DNAN基含铝炸药RA1中的铝粉，制备得到相应的含LiF炸药RF1，通过对RF1炸药进行圆筒试验，可获得剔除了铝粉反应影响的圆筒试验结果。试验制备的两种DNAN基熔铸炸药RA1和RF1的组分配比与物理性质如表1所示。

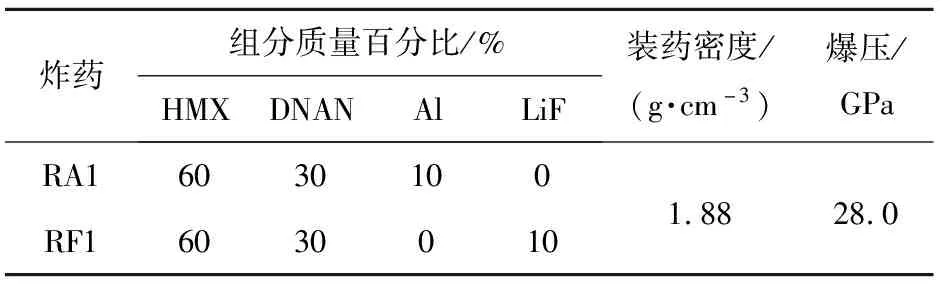
表1 RA1与RF1炸药的组分和物理性质

对RA1和RF1两种炸药分别进行2发圆筒试验，φ50 mm圆筒试验测试系统如图1所示，其中金属圆筒材料为TU1无氧铜，密度为8.930 g/cm3，圆筒内径为φ50 mm，壁厚为5 mm，长度为500 mm.试验过程中在圆筒的顶端和底端分别布置2个电探针，用于测试圆筒内炸药的爆速。为确保炸药形成稳定爆轰、减小爆速测试的不确定度，在传爆药与圆筒顶端之间采用了尺寸为φ50 mm×50 mm的过渡药柱，其与圆筒内炸药为同种炸药。

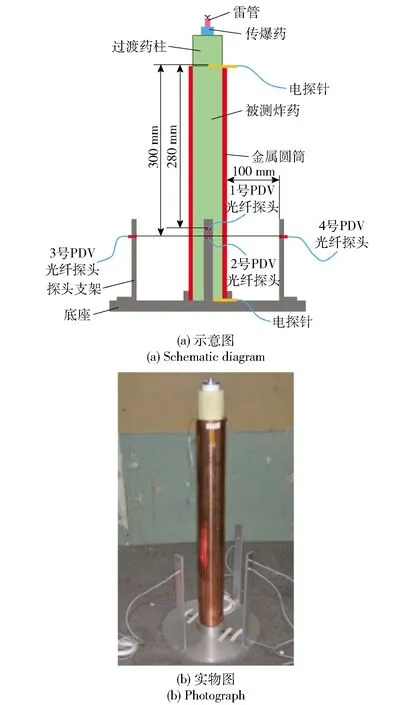
图1 φ50 mm圆筒试验测试系统

待爆轰波传入装填在圆筒内的被测炸药后，炸药爆轰产物会驱动圆筒壁向外做膨胀运动，在距圆筒顶端一定距离处布置PDV光纤探头，可记录相应位置的圆筒壁膨胀速度。如图1所示，PDV光纤探头用支架固定，在距圆筒顶端280 mm处布置1个探头(编号为1号)，在300 mm处布置3个方向不同的探头(编号分别为2号、3号、4号)，探头均与圆筒表面垂直，距离均为100 mm.测试所用PDV光纤探头的直径为3.2 mm，探头输出激光的焦斑直径小于0.3 mm，采用窗口傅里叶变换方法将探头测得的原始频域干涉信号进行处理，变换为时域信号，即可获得相应的圆筒壁面膨胀速度，速度时间分辨率为15 ns[14].1发试验可获得4个测点处的圆筒壁膨胀速度，通过对比280 mm和300 mm两测点处的速度曲线，可以确定在测试区域炸药是否形成了稳定爆轰，从而验证试验结果的可靠性，而通过对比300 mm 3个测点处的速度曲线，可验证试验系统的一致性和稳定性。

2 试验结果与分析

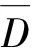
表2 RA1与RF1炸药的爆速测试结果

RA1和RF1两种炸药圆筒膨胀速度试验结果如图2所示，可知每发试验中各测点处PDV 探头测得的速度曲线重合度均较高，表明本文建立的圆筒试验测试系统可靠性较高，获得的试验数据一致性较好，测试精度也较高。同时，试验曲线第1个起跳峰值点对应的圆筒壁面膨胀速度与测点处爆轰波阵面上的压力相关，由于280 mm处测点与300 mm处测点测得曲线的第1个起跳峰值点重合度较高，表明炸药内部的爆轰波传播稳定，圆筒内炸药已形成稳定爆轰，因此所得试验结果可用于确定RA1和RF1炸药的爆轰产物状态方程参数。

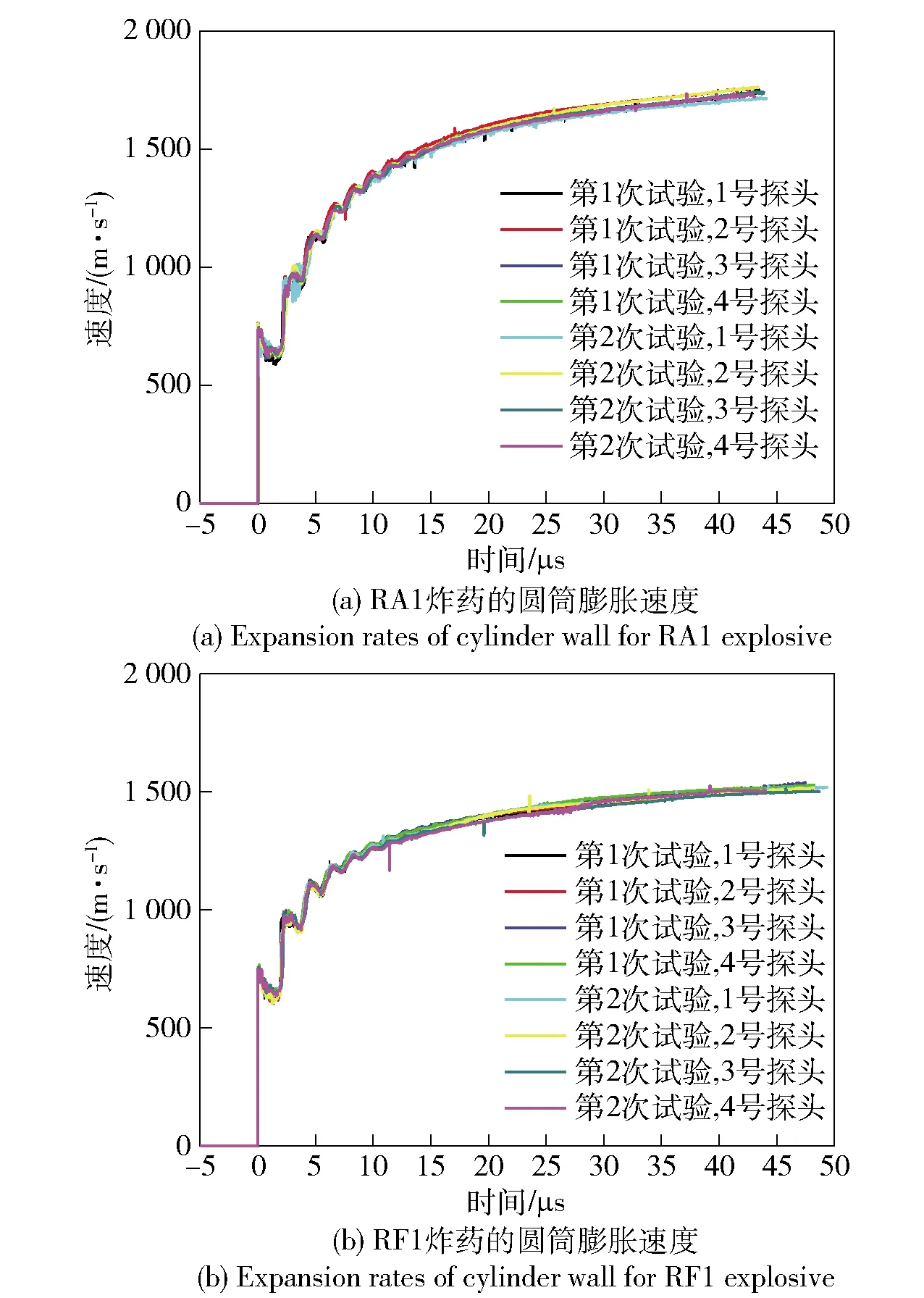
图2 圆筒试验测试结果

由于试验曲线一致性较好，为了便于后续对试验数据的对比分析，分别对RA1和RF1炸药的8条试验曲线取平均，则RA1和RF1炸药圆筒膨胀速度试验结果的对比如图3(a)所示，RA1与RF1炸药圆筒膨胀速度比值vRA1/vRF1变化曲线如图3(b)所示。由图3(a)可知，RA1和RF1炸药的圆筒膨胀速度曲线在初始阶段(0～4.6 μs)几乎重合，而在4.6 μs时刻左右，两条曲线开始分离，RA1炸药的圆筒膨胀速度开始超过RF1炸药，最终在RA1炸药作用下圆筒壁达到的最大膨胀速度(1 738 m/s)比RF1炸药作用下圆筒壁的最大膨胀速度(1 523 m/s)高约14%，可知铝粉的添加显著提高了含铝炸药爆轰产物的金属加速做功能力。

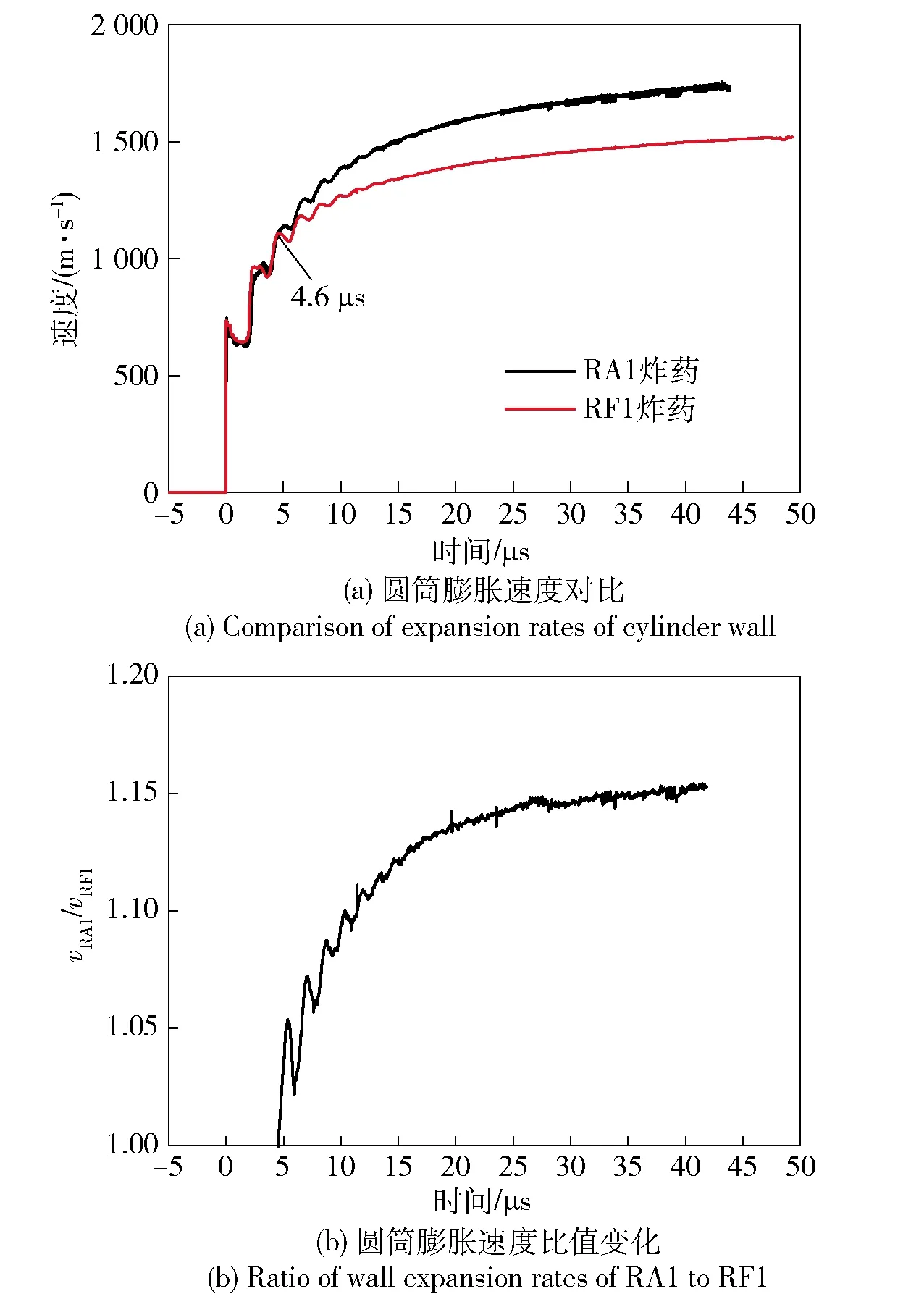
图3 RA1和RF1炸药圆筒试验结果对比

由于RF1炸药中的LiF是化学惰性的，其爆轰产物仅为炸药组分化学反应产生的气体产物，则在RF1炸药的圆筒试验过程中，圆筒壁的径向膨胀运动仅由炸药组分的爆轰产物驱动。RA1和RF1炸药圆筒膨胀速度曲线在初始阶段(0～4.6 μs)的高度重合表明，在爆轰驱动初期阶段，RA1含铝炸药中铝粉参与反应的程度较低，此时爆轰产物主要由炸药组分反应产生，其产物的组成、物理状态与驱动做功能力等性质均与RF1炸药爆轰产物相近，其爆轰产物可等同于RF1炸药的爆轰产物。然而，随着爆轰反应的进行，反应流场中压力和温度的不断升高使得铝粉的反应量逐渐增加，由于铝粉与爆轰产物发生二次燃烧反应时会释放出大量能量，加速圆筒壁的膨胀，提高爆轰产物的驱动做功能力，因此在4.6 μs以后，RA1炸药圆筒膨胀速度的增长速率大于RF1炸药，二者试验曲线发生明显分离。

综上所述，在含铝炸药爆轰反应初始阶段，铝粉反应量很少可近似忽略，由于冲击起爆过程中炸药内部的压力、温度等均低于爆轰反应初始阶段，铝粉参与反应的程度更低。则可推得RA1含铝炸药冲击起爆过程中的爆轰产物也可等同于RF1炸药的爆轰产物，从而利用RF1炸药圆筒试验数据确定的爆轰产物状态方程参数，可用于描述RA1含铝炸药冲击起爆过程中爆轰产物的状态。

将RA1和RF1炸药的圆筒膨胀速度分别进行积分，即可得到两种炸药作用下圆筒壁膨胀距离ΔR随时间的变化曲线，如图4所示。由图4可知，在爆轰驱动的初期阶段，RA1和RF1炸药圆筒膨胀位移曲线的差别难以分辨，大约在10 μs以后二者才有明显差别，这表明与高速扫描相机测试方法相比，采用PDV测速技术直接测量圆筒壁膨胀速度的试验方法可以获得更多圆筒膨胀过程的细节，测试结果的精度更高，同时减少了数据处理过程中人为因素(如圆筒膨胀起始点的判读等)的影响。

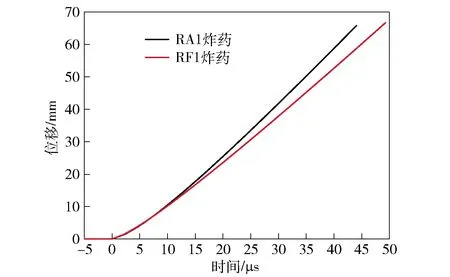
图4 RA1和RF1炸药圆筒膨胀位移的对比

3 爆轰产物状态方程参数确定

选取合适的爆轰产物状态方程，利用第2节RA1和RF1炸药的圆筒膨胀速度试验结果，结合遗传优化算法和数值模拟技术，即可分别确定RA1和RF1炸药的爆轰产物状态方程参数。RA1炸药的产物状态方程参数可用于评估RA1炸药的产物驱动做功能力，而RF1炸药的产物状态方程参数可用于描述RA1炸药冲击起爆过程中的爆轰产物状态。

在爆轰反应过程的C-J面后，LiF仍然保持化学惰性，含LiF炸药RF1的爆轰产物膨胀过程是等熵的，则可采用标准形式的Jones-Wilkins-Lee(JWL)状态方程描述其爆轰产物，方程形式为

(1)

(2)

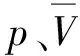
(3)

(4)

(5)

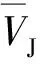
在确定RF1炸药的爆轰产物状态方程参数时，首先假设一组R1、R2、ω，代入上述基本关系方程组后，可求得对应的A、B、C，即获得一组JWL状态方程初始参数。然后采用二维流体动力学计算软件，建立圆筒试验测试系统的二维计算模型，并输入该组初始参数对圆筒试验进行计算。将圆筒壁膨胀速度的计算结果和试验结果进行对比，若二者之间的误差不满足精度要求，则利用遗传算法不断调整参数R1、R2和ω的取值，并重复上述过程，直至试验结果和计算结果满足精度要求。利用上述方法，本文确定的RF1炸药爆轰产物JWL状态方程参数如表3所示，RF1炸药圆筒试验数据和数值模拟结果的对比如图5所示。

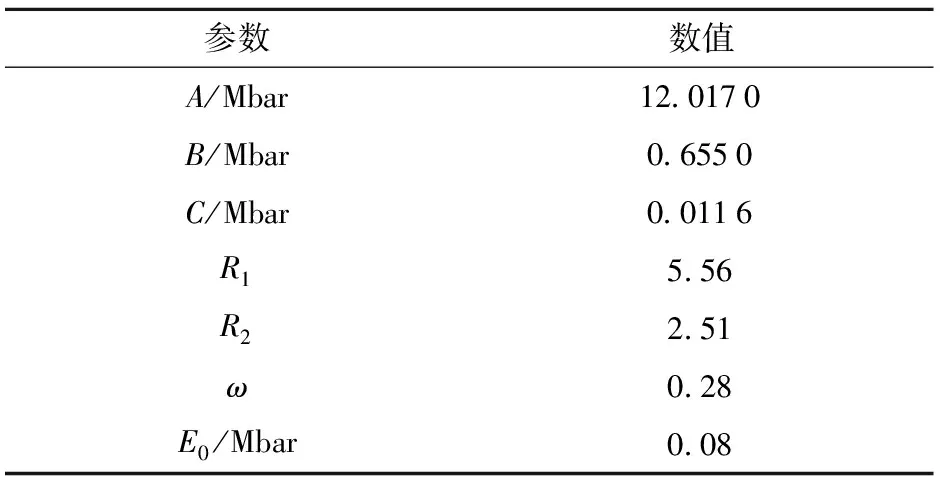
表3 RF1炸药爆轰产物JWL状态方程参数

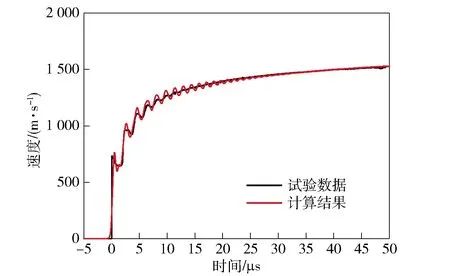
图5 RF1炸药圆筒试验数据与数值模拟结果对比

对于含铝炸药RA1，爆轰反应中C-J面后铝粉与产物气体发生二次燃烧反应释放的能量，使得其爆轰产物的膨胀过程是非等熵的，且当铝粉反应量不同时，铝粉释能对爆轰产物膨胀过程的影响也不同，因此(1)式所示的JWL状态方程不再适合描述含铝炸药的爆轰产物。为此，Miller等[23]对其进行了改进，通过增加后续释能项，提出了JWL-Miller形式的含铝炸药产物状态方程，其方程形式为

(6)

式中：λ为铝粉反应度，即已反应铝粉的质量与含铝炸药中铝粉总质量之比；Q为铝粉反应附加比能。与JWL状态方程相比，JWL-Miller状态方程在保持JWL状态方程参数不变的基础上，仅额外增加了铝粉的能量释放参数λQ，以唯象地描述含铝炸药中铝粉二次反应对冲击波能量的补充。铝粉二次反应的反应速率方程为

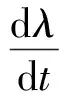
(7)

式中：a为能量释放常数；m为浓度指数；n为压力指数。

当铝粉反应度λ=0时，含铝炸药RA1的产物状态方程仅由参数A、B、C、R1、R2和ω确定。在爆轰驱动初始阶段，铝粉反应量较少，RA1炸药的爆轰产物可等同于RF1炸药的爆轰产物，则RA1炸药JWL-Miller产物状态方程参数中的A、B、C、R1、R2和ω应与RF1炸药相同。因此，仅需调整铝粉的二次反应速率方程参数a、m、n，结合遗传优化算法及数值模拟计算，通过对比RA1炸药圆筒膨胀过程的试验结果与数值模拟结果，则可确定RA1炸药的爆轰产物JWL-Miller状态方程参数。当Q=0.04 Mbar时，含铝炸药RA1的二次反应速率方程参数如表4所示，RA1炸药圆筒膨胀速度试验结果与数值模拟结果的对比如图6所示。

表4 RA1炸药二次反应速率方程参数

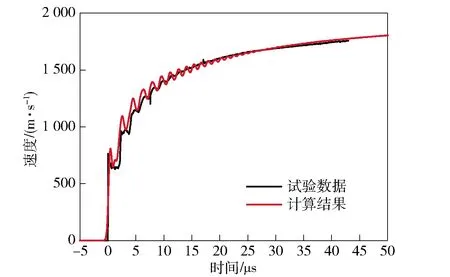
图6 RA1炸药圆筒试验数据与数值模拟结果对比

4 结论

本文基于PDV测速技术建立了φ50 mm圆筒试验测试系统，对DNAN基熔铸含铝炸药RA1和含LiF炸药RF1进行了圆筒试验研究，并利用遗传优化算法和数值模拟技术，分别确定了RA1炸药和RF1炸药的产物状态方程参数。得出以下主要结论：

1)在爆轰驱动的初期阶段，铝粉反应量较少，RA1与RF1炸药的圆筒速度曲线高度重合，表明二者爆轰产物的物理状态、驱动能力等非常接近。但随着铝粉反应量的增加，RA1与RF1炸药的圆筒速度曲线出现明显分离，含铝炸药RA1的产物驱动能力显著提高。

2)在含铝炸药爆轰反应初始阶段以及冲击起爆过程中，铝粉的反应量都很少可近似忽略，其爆轰产物均可等同于同样配方含LiF炸药的爆轰产物，则同样配方含LiF炸药的产物状态方程参数可用于描述含铝炸药冲击起爆过程中的产物状态。

3)要确定含铝炸药的爆轰产物JWL-Miller状态方程参数，需先确定同样配方含LiF炸药的爆轰产物JWL状态方程参数，然后才能确定铝粉的二次反应速率方程参数，因此要得到带铝粉二次反应的含铝炸药爆轰产物状态方程参数，需同步测量同样配方含LiF炸药的爆轰驱动过程。

致谢国防科技大学张震宇副教授为本文数值模拟研究提供的帮助和支持。