基于纵程解析解的飞行器智能横程机动再入协同制导
2021-08-28张晚晴余文斌李静琳陈万春
张晚晴,余文斌,李静琳,陈万春
(1.北京航空航天大学 宇航学院, 北京 100191; 2.北京宇航系统工程研究所, 北京 100076)
0 引言
高超声速滑翔飞行器具有飞行速度快、反应时间短、打击精度高、作战半径大等特点[1],在现代化战争中具有良好的应用前景,近年来成为世界各国广泛关注的焦点。与此同时,针对高超声速目标威胁,各国相继研发了多种防空反导武器系统,大大降低了单个高超声速滑翔飞行器的突防能力和作战效能。因此,发展多高超声速滑翔飞行器协同打击技术,提高对防空反导武器系统的突防概率,成为当前各国学者的研究热点[2]。
高超声速飞行器协同饱和打击任务要求飞行器具备一定程度上自由调节自身飞行时间的能力,同时在指定时间范围内实现对目标的精确打击。在高超声速飞行器再入制导过程中,再入滑翔段是飞行距离最远、空域跨度最大、气动特性变化最为剧烈的一段,其制导与控制系统设计也最为复杂。传统针对末制导段的协同方法多基于定常速度运动模型或小角度线化模型设计[3],难以直接应用到再入协同制导方法设计中,因此如何设计具备飞行时间可控能力的再入制导方法是一个研究难点。
现阶段的再入制导方法主要分为两种:标准轨迹制导法[4-7]和预测-校正制导法[8-10],在这两种典型方法的基础上,又衍生出了标准轨迹与落点预测混合制导方法,这3种制导方法主要是针对纵向飞行轨迹。在侧向平面,高超声速飞行器采用倾斜转弯(BTT)模式,通过倾侧反转逻辑来控制飞行器侧向机动。但目前大多数再入制导问题未考虑时间约束,对协同再入制导的研究较少。
关于时间可控再入制导可以归结为纵向弹道调整与横向倾侧反转设计。文献[11]基于模型预测静态规划设计了协同再入制导方法,但该方法并未对终端速度与高度进行约束管理,难以满足工程实际需求。文献[12]分析了影响飞行时间的因素,基于反向传播(BP)神经网络提出一种时间可控再入制导方法。该方法通过BP神经网络在线预测剩余飞行时间,进而调整航向角走廊宽度以改变飞行时间。仿真论证可知,该制导方法时间调整范围为整个再入时间的4%~5%,时间可控范围较窄,不适用于复杂的协同任务需求。Yu等[13]将纵程制导倾侧角剖面表示为能量的线性函数,基于三维弹道解析解与时间解析解调整倾侧角剖面参数,用当前剩余飞行时间和剩余射程与事先规划弹道的偏差来修正由横向倾侧反转引起的时间偏差,实现了对再入飞行时间的精确控制。Li等[14]同样将倾侧角剖面参数化,纵程采用数值积分预测剩余射程与剩余时间,进而实现对倾侧角剖面的修正,横程采用剩余时间进一步修正倾侧反转时刻。其制导方法虽然实现了对飞行时间的控制,但是终端倾侧反转次数较多,不利于控制系统跟踪。文献[15]在高度-速度剖面内设计了参考轨迹,通过在线数值预测剩余飞行航程和时间。而后校正两个轨迹参数以满足航程和时间约束并求取实际控制量,结合侧向航向角走廊实现了单飞行器的时间约束再入制导。文献[16]将再入过程划分为两个阶段,第1个阶段通过倾侧角剖面去实现期望攻角约束,第2个阶段通过调整攻角剖面进而实现攻击时间约束。
由于时间可控再入制导的复杂性与制导实时性要求,常规再入制导方法难以简单应用到协同问题上。随着智能算法的兴起,强化学习在一些决策问题上的出色表现为再入制导设计提供了可行的探索方向[17-18],并且其离线训练-在线使用模式具有较强的适应性与实时性。文献[19]结合了强化学习与神经网络,运用确定性策略梯度下降的深度神经网络(DDPG)算法设计倾侧角剖面,实现了再入制导设计。文献[20]提出了一种飞行时间约束的再入制导方法,该制导方法纵向制导运用数值预测-校正计算倾侧角,横向制导将倾侧反转逻辑视为马尔可夫决策问题,运用强化学习寻找满足时间和射程约束的横向制导最优策略,但其未考虑地球自转引起的惯性力,不适用于实际再入飞行过程。文献[21]将飞行环境构建为包含千万量级状态点的状态空间,采用强化学习算法训练制导模型参数,纵向制导依然采用基于定攻角剖面的倾侧角迭代方法,横向制导则利用Q-学习算法训练横向翻转决策器。虽然智能决策结果使再入飞行器在复杂任务中可以发挥其较强的机动能力,但是仿真结果命中精度不及传统的预测-校正制导方法。
相比于数值预测-校正制导方法,基于弹道解析解的制导方法能够对再入弹道进行精准预测,减少在线计算时间,满足工程上实时应用的需求。而强化学习类方法凭借其处理复杂模型、受扰动模型,甚至无模型情况下控制问题所具有的设计流程通用性、自学习自适应能力、泛化能力强的特点,逐步运用于飞行器制导方法设计中。
基于以上分析,本文提出一种基于纵程解析解的横向智能机动再入协同制导方法。基于旋转地球模型,本文首先给出基于纵程解析解的纵向制导方法结构,之后引入深度Q-学习网络(DQN)进行横向倾侧反转规划策略设计,实现位置、飞行时间、能量管理等多约束协同再入制导,并通过仿真进行验证。
1 时间协同再入问题描述
1.1 动力学模型
旋转地球模型下,高超声速飞行器的6自由度动力学方程[6]为
(1)
(2)
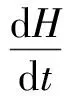
(3)
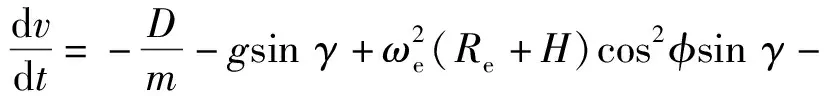
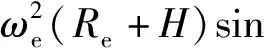
(4)
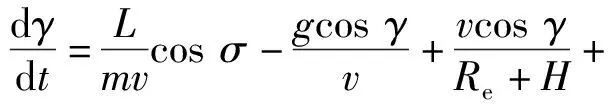
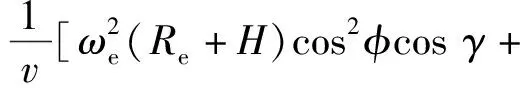
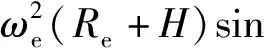
2vωecosφsinψ],
(5)
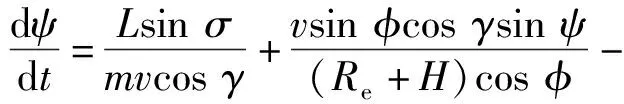
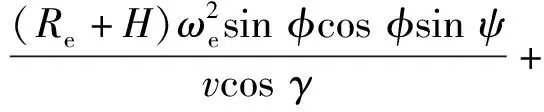
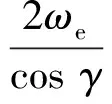
(6)
式中:λ为经度;t为时间;v为飞行器相对于地球固连坐标系的速度;γ为弹道倾角;ψ为飞行器航向角,以当地北向为基准;Re为地球半径,Re=6 378.137 km;H为海拔高度;φ为纬度;D为阻力,D=0.5ρv2SCD,ρ为大气密度,S为飞行器参考面积,CD为阻力系数;m为飞行器质量;g为重力加速度;ωe为地球自转角速度;L为升力,L=0.5ρv2SCL,CL为升力系数;σ为倾侧角。
1.2 过程约束
高超声速飞行器滑翔段过程约束为
(7)
(8)
(9)
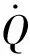
1.3 终端约束
本文研究的再入段终点严格来说并非是一个点,而是一定大小的区域,飞行器在进入该区域的同时也要保证具有相应的速度大小和方向。定义tf为再入段终止时刻,则终端约束设计为λ(tf)=λd、φ(tf)=φd、v(tf)=vd、H(tf)=Hd、tf=td、Rtm(tf)=Sd、σd≈0°、γd≈0°、Δψd≈0°,λd、φd、vd、Hd、td、σd、γd、Δψd分别为期望的终端经度、终端纬度、终端速度、终端高度、终端时间、终端倾侧角、终端弹道倾角、终端航向角误差,Rtm为飞行器与目标之间的距离。
2 基于纵程解析解的智能横程机动再入协同制导设计
根据再入弹道的特性,将其划分为初始下降段、平稳滑翔段和高度调整段3部分[6]。制导方法流程如图1所示。
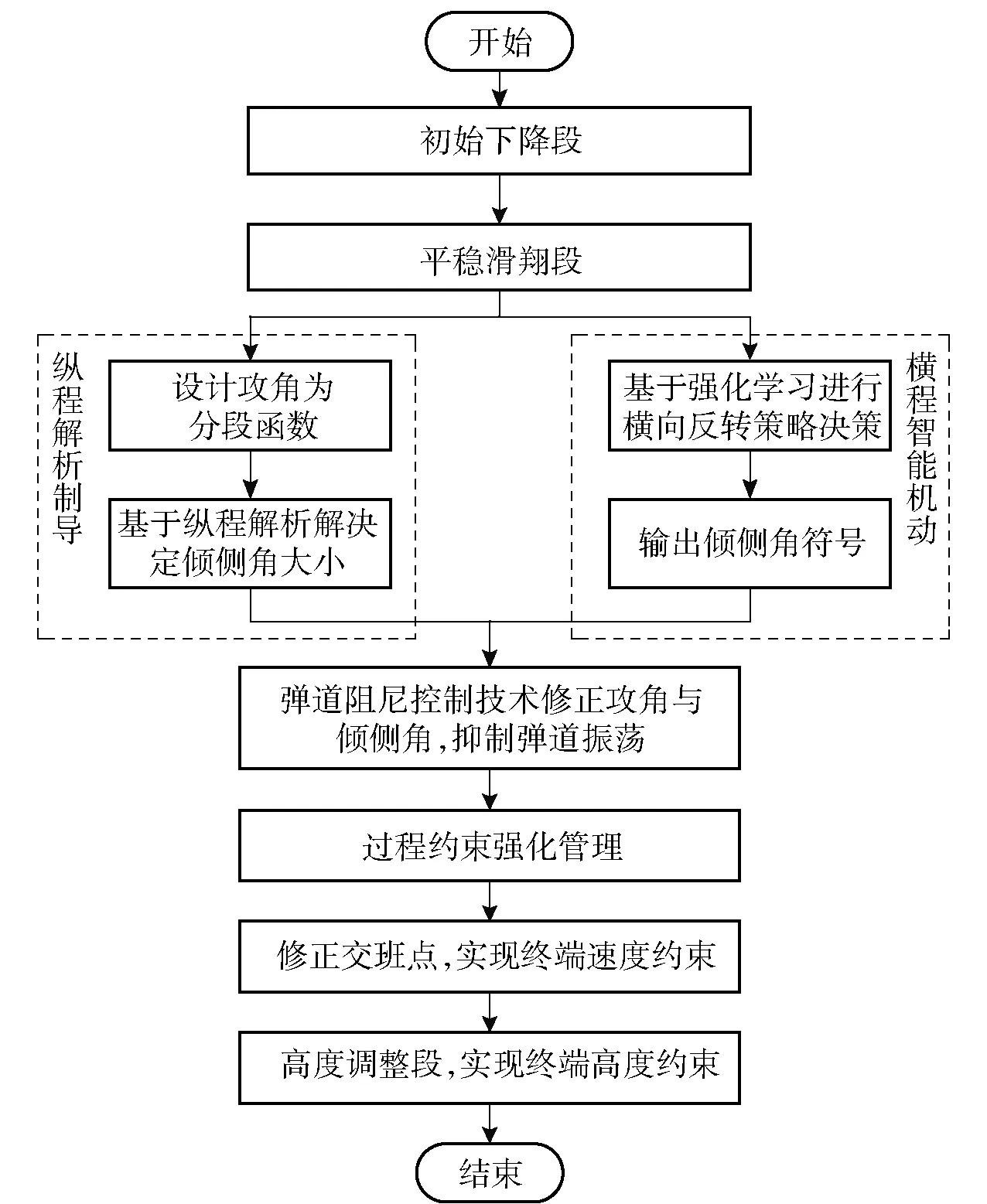
图1 基于纵程解析解的智能横程机动再入协同制导方法流程
2.1 初始下降段
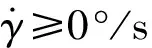
(10)
σc=0°,
(11)
Δγ=γ-γG,
(12)
(13)
式中:kγ为反馈系数,kγ=5;γG为平稳滑翔弹道倾角,
(14)
hS为标称高度。(14)式是令弹道倾角2阶导数为0°/s2平稳滑翔条件下求得的平稳滑翔弹道倾角[7]。当Δγ=0°时,飞行器进入平稳滑翔阶段。
2.2 基于纵程解析解的平稳滑翔段纵向制导
2.2.1 基准攻角剖面设计
鉴于纵程解析解[6]是以能量为自变量设计的,为更方便地利用解析解,本文提出的制导方法中所有的参考剖面均采用单位能量E作为自变量。设计参考攻角剖面αb为
(15)
式中:αi和αf分别为基准攻角剖面设计初值参数和终值参数;Eα为参考攻击剖面的分段函数转换点,位于平稳滑翔段与最后的高度调整段的交界点附近,设为Eα=-5.55×107J/kg;Ed为期望终端能量。为发挥出飞行器的最大能力,设计攻角为最大升阻比对应攻角,即αi=10°.设计攻角为能量的二次函数是为了使攻角可以从αi平缓地过渡到αf.在本文制导方法中,设计αf=6°.当攻角剖面设计完成时,相应的参考升阻比Kb也随之确定。
2.2.2 基准升阻比剖面设计
为满足射程要求,设计参考纵向升阻比剖面KLb为
KLb=
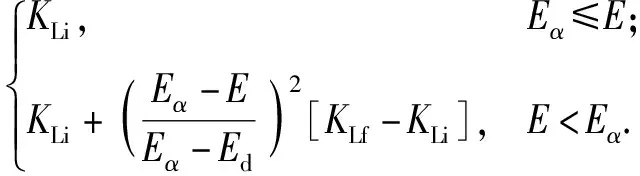
(16)
式中:KLi和KLf分别为基准升阻比剖面设计初值参数和终值参数。
令纵程解析解等于剩余射程,即可求得KLi.设计KLf=Kd是为了使得终端的倾侧角为0°,其中Kd是终端时刻的升阻比。通过设计(16)式的形式,可在飞行过程中控制倾侧角近似为常值。
为求解KLi,首先需要计算剩余飞行射程xDf.在地心旋转坐标系下[6],定义η为从地球中心指向飞行器的矢量与从地球中心指向目标的矢量之间夹角。考虑到滑翔段中飞行器的高度变化相较于地球半径而言量级较小,对生成倾侧角指令影响较小,此处忽略高程变化因素,则剩余飞行射程可表示为
xDf=Reη-Sd,
(17)
式中:Sd为再入段结束时到目标的距离。求解KLi的过程可见文献[6],结果为:
当E≥Eα时,有
(18)
(19)
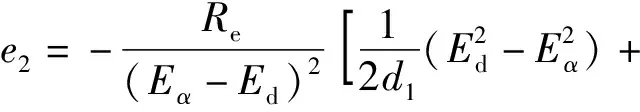
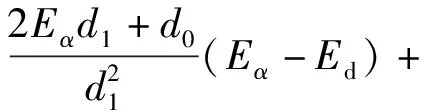
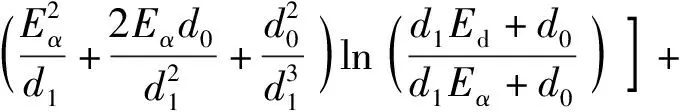
(20)
(21)
(22)
R*=Re+H,μ为引力常量,hij(i=1,2;j=0,1)、α1和γ1均为常值系数,具体求解方法见文献[6]。
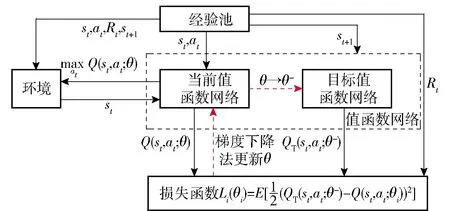
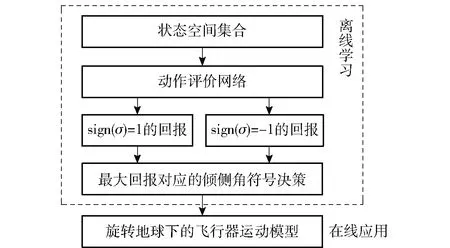
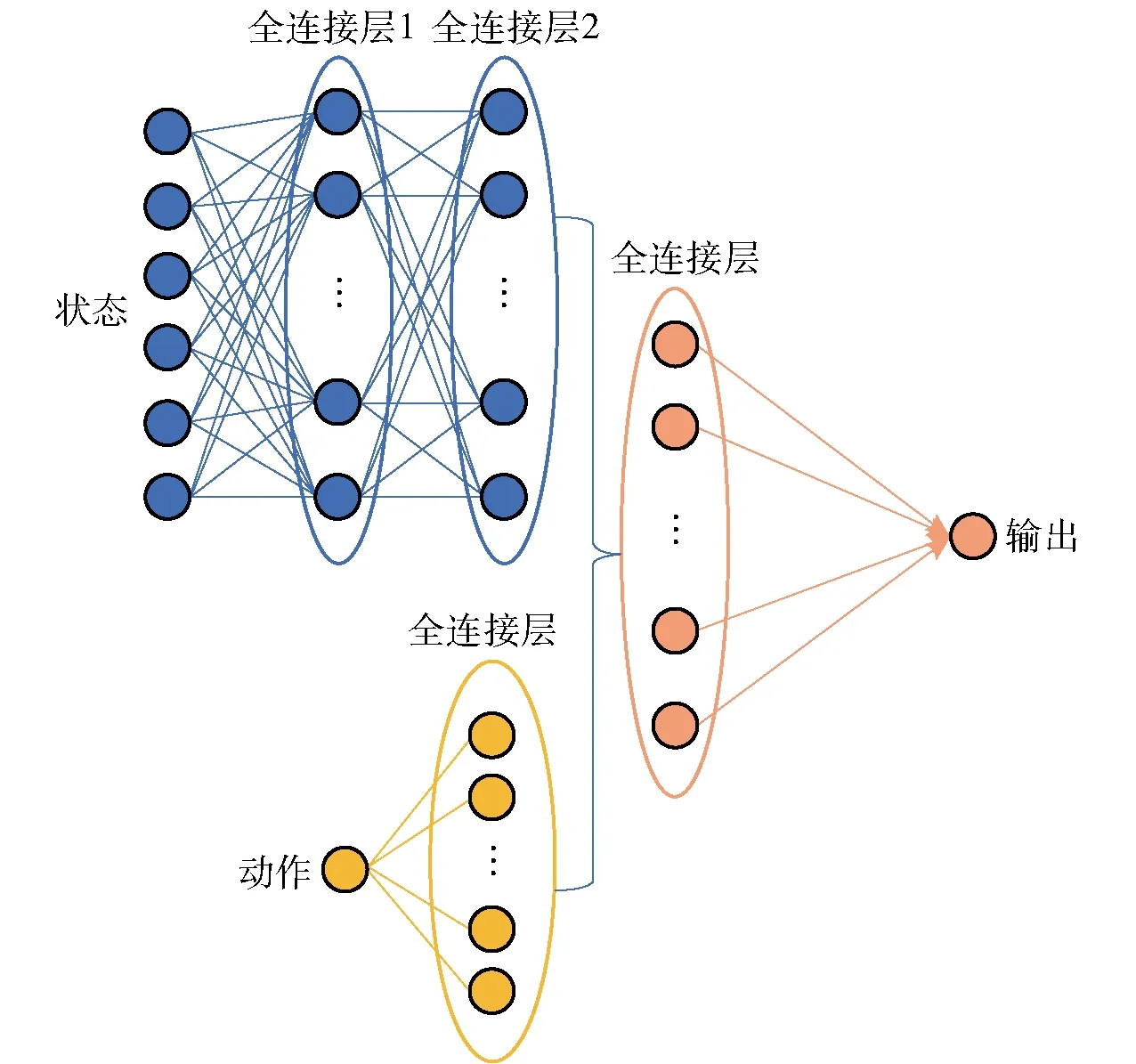
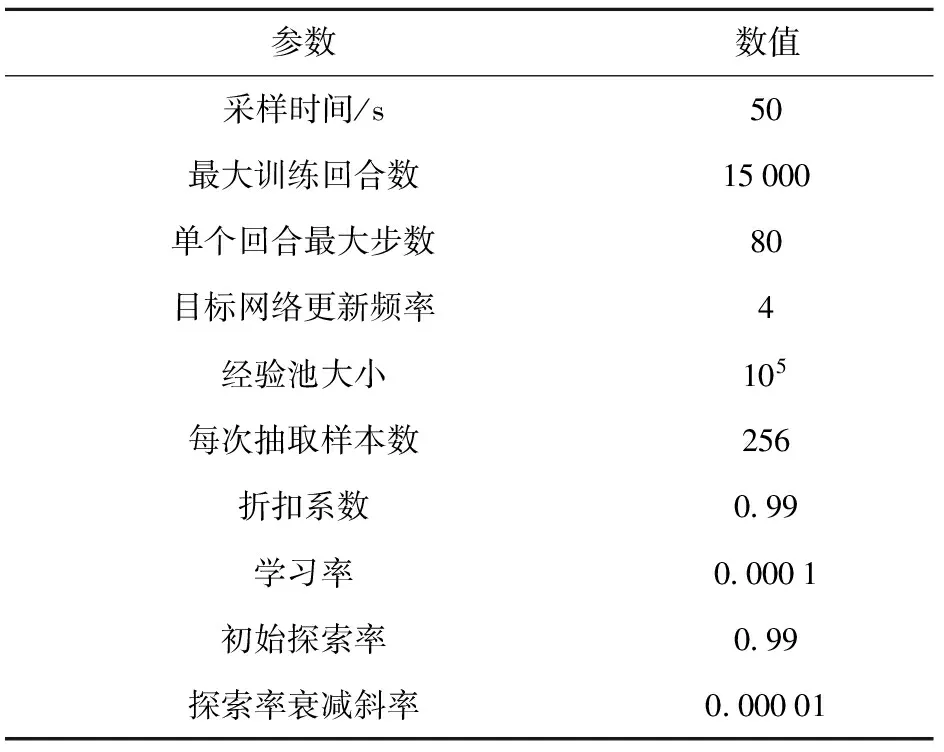
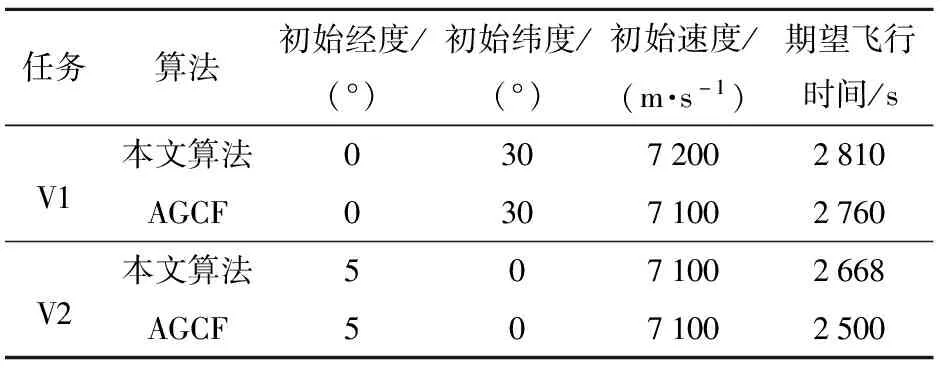
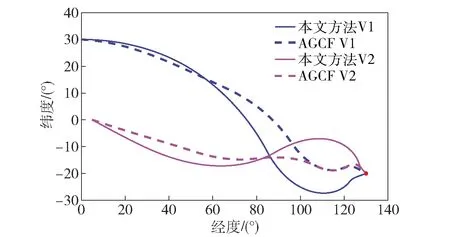
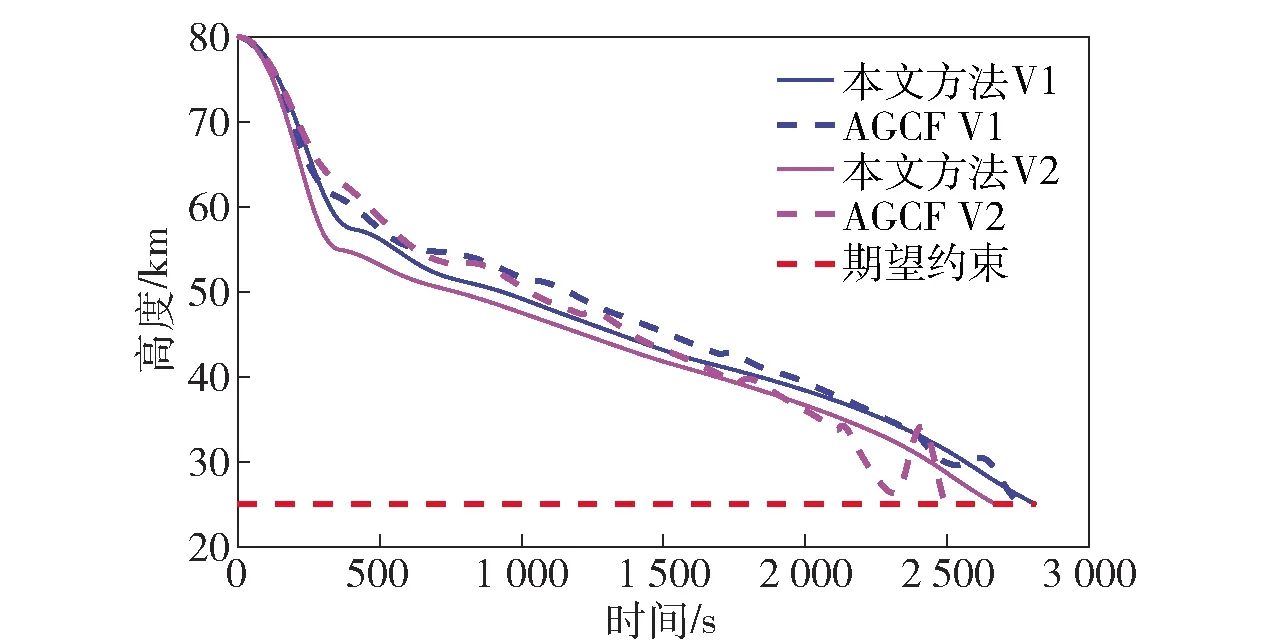
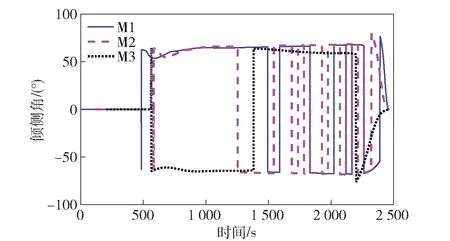
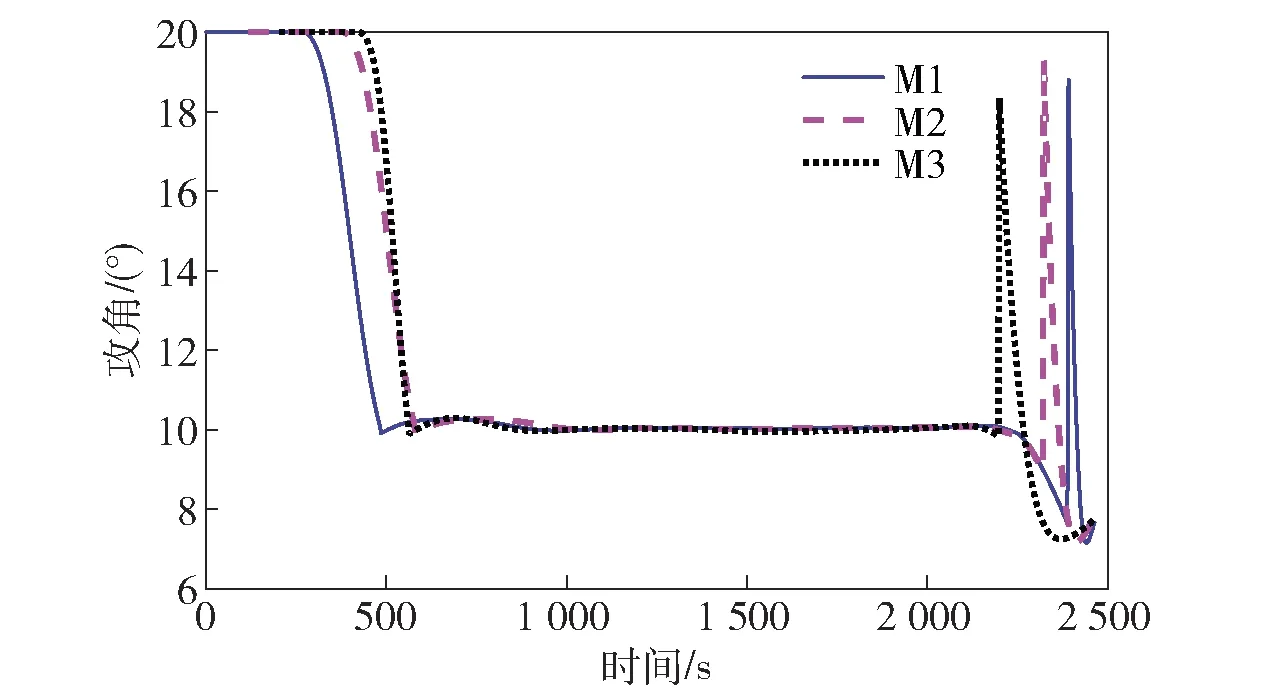
当E 文献[12]中分析表明,不同的航向角走廊宽度,即不同的横向倾侧反转机制设计,会影响飞行航程,进而影响飞行时间。由于再入飞行时间与横向反转策略的关系非线性程度很高,二者的关系难以解析表达,因此传统的横向制导策略方法将无法适用于解决飞行时间约束问题。 考虑到高超声速飞行器再入横向倾侧反转规划本质上是一个典型的二值决策问题,即根据当前状态和目标给出倾侧角符号“+”或“-”,因此本文基于强化学习方法设计再入横向制导智能决策器,通过调节倾侧角符号实现再入飞行时间的可控性。 解决强化学习问题的框架是马尔可夫决策过程[22],由元组(S,A,P,R,η)描述,其中:S为有限的状态空间,且任意状态s∈S;A为有限动作空间,且任意动作a∈A;P为状态转移概率;R为回报函数;η为折扣因子,η∈[0,1],用来计算累积回报[23]。其目标是找到最优策略π,使得该策略下总回报最大。 2.3.1 基于DQN算法的横向制导 考虑到再入横向制导问题是一个状态空间连续、动作空间离散的问题,选择DQN算法进行横向制导方法设计[24]。 DQN算法是一种将Q-学习和深度学习相结合的强化学习算法,其算法结构如图2所示。在每个训练周期内,DQN算法随机抽取来自经验池的样本对两个网络进行训练。使用一个网络产生当前状态-动作值函数Q(st,at;θ),其中st和at分别表示当前时刻的状态和动作,θ为网络参数。使用另一个网络产生目标状态-动作值函数,表示为 图2 DQN算法结构 QT(st,at;θ-)= (23) 式中:θ-为该网络参数;Rt为当前时刻期望值;stf为终端时刻状态。在训练过程中,DQN根据网络参数θ的动作评价网络对当前状态st下能够采取的动作集A中所有动作的价值Q(st,at;θ)进行估计,输出其中具有最大价值的动作;之后根据最大价值动作的实际价值与估计值之间的误差对参数θ进行更新。为保证网络具有一定的探索能力,定义探索率ε,使得每次输出均存在概率ε进行随机动作选择。 根据Q(st,at;θ)的Bellman方程形式,神经网络训练中,定义第i次迭代的损失函数为 (24) 式中:θi为第i次迭代网络参数。经过一段时间的学习后,采用梯度下降法用新的θi更新目标值函数网络参数θ-,可以在一定程度降低当前Q值和目标Q值的相关性,提高算法稳定性: (25) 2.3.2 马尔可夫决策过程建模 首先对横向飞行过程进行马尔可夫决策过程建模。考虑到由横向飞行状态控制再入飞行时间,并综合射程、落点误差和能量管理要求,构建状态归一化空间S为 (26) (27) (28) (29) (30) (31) (32) 式中:λgo、φgo分别为剩余经度和剩余纬度,λgo=λd-λ,φgo=φd-φ;v0为再入初始速度;Sgo为剩余射程,Sgo=Reη;tgo为剩余飞行时间,tgo=td-t;下标0表示初始时刻的状态,如λgo0与φgo0分别为初始时刻的剩余经度与剩余纬度。 由于倾侧角符号仅有正、负两个选项(当倾侧角大小为0°时视为符号为正),设符号函数表示为sign(·),因此动作空间集合A为 A=sign(σ)={1,-1}. (33) 再入制导问题是一个多约束问题,需要满足落点偏差、飞行时间、终端速度、终端高度、过程约束等多项指标,存在的可行解范围较窄,因此回报函数的合理设计对再入问题至关重要。考虑到本文中终端速度、高度约束由纵向制导设计决定,横向制导主要考虑射程与时间约束。所以结合混合回报函数设计方法,将回报函数R(stf)设计为阶梯状,如(34)式所示: R(stf)= (34) 式中:ΔSgo为射程误差,ΔSgo=Sgo(tf)-Sd;Δtgo为飞行时间误差,Δtgo=tf-td;B为倾侧反转次数;ξB为反转次数权重值,ξB越大,横向决策器会倾向于向倾侧反转次数较少的方向学习。本文选择ξB=5、ξB=10与ξB=20分别进行学习,其中ξB=5和ξB=10的学习效果如图3所示。由图3可以看出,当ξB减小时,收敛速度加快,但是训练出来的结果倾侧反转次数会较多。 训练结束后,在线应用生成的智能体进行横向倾侧决策,即可以实现再入协同制导。制导流程如图4所示。 图4 基于DQN算法的智能横向机动决策器 KHb=sign·|KHb|, (35) 式中:sign为表示倾侧反转方向的符号变量。得到横向升阻比剖面后,参考倾侧角剖面σb也随之确定,表示为 (36) 式中:Kr表示实际的升阻比。为保证参考剖面的跟踪精度,这里采用了弹道阻尼控制技术[7]来抑制再入弹道存在的长周期、弱阻尼的振荡。设计指令攻角αc与倾侧角σc分别为 (37) (38) 式中:KγG是弹道阻尼控制系数的反馈系数,取值为5.平稳滑翔段需要满足过程约束,故将(7)式~(9)式的过程约束转变为倾侧角约束,表示为 (39) (40) (41) (42) 式中:Hmin对应滑翔高度的最低边界,可以通过过程约束求得;kσ为常值系数,kσ=-50.因此,为满足过程约束,倾侧角需要满足: |σc|≤σmax. (43) 设平稳滑翔段与高度调整段的交班点能量为EA.当能量E 2.5.1 交班点能量EA调整算法 为严格满足终端高度约束,且使得末段弹道更加平滑,高度调整阶段设计采用三维比例导引律进行制导。通过对平稳滑翔段制导方法的分析可知,如果减小EA,制导方法指令将会产生更大的倾侧角以消除最后一次倾侧反转时产生更大的航向误差,从而使纵向升阻比减小,降低终端速度vf.因此,vf可视为关于EA的单调函数。为保证终端约束,这个问题可视为求解非线性方程vf(EA)=vd解的问题。这里采用割线法进行求解,通过多次弹道仿真对vf进行预测,并根据预测值与终端约束的偏差调整EA的值: (44) 2.5.2 高度调整段制导方法 当飞行器进入高度调整阶段后,本文采用三维比例导引制导方法进行控制。在航迹(FP)坐标系[25]下,指令加速度矢量为 (45) (46) (47) 式中:γLOS、ψLOS分别表示纵向平面视线角与横向平面视线角, (48) (49) (50) (51) (52) 横向平面内机动加速度指令为 (53) 因此可得参考倾侧角σb为 (54) 升力加速度大小为 (55) 则升力系数为 (56) 则可根据升力系数与马赫数反求得攻角αb[27].注意攻角需要满足过程约束,即αb∈[αmin,αmax],其中αmin与αmax分别为飞行器许可攻角的最小值与最大值。 为了满足过程约束,与2.4节相同,倾侧角仍然需要满足|σc|≤σmax,其中σmax可由(39)式计算得到。 再入飞行器模型选择CAV-H[27]飞行器,其质量为906.4 kg,参考面积为0.483 87 m2.本文采用的DQN算法网络结构如图 5所示,隐藏层神经元节点数均为200,采用ReLU激活函数。 图5 DQN网络结构 网络参数设定如表1所示。对于高超声速再入飞行过程,采样时间如果设置过短,可能会造成飞行器频繁反转,降低寻找最优解效率。若采样时间过长,则有可能遗漏更优策略。考虑高超声速飞行器再入飞行时间较长,且较为频繁的倾侧反转会影响控制系统的稳定性,这里设置采样时间为50 s. 表1 DQN网络参数设置 为了验证本文提出的基于纵程解析解的智能横程机动再入协同制导方法有效性,在标称条件下,与Yu[13]提出的基于三维解析解的再入协同制导方法(AGCF)以两个再入任务案例进行仿真对比分析。任务初始设置条件如表2所示。再入初始高度为80 km,两个任务均打击同一目标点,目标经纬度坐标为(0°,-30°)。终端射程约束为Sd=50 km,终端高度约束为Hd=25 km,终端速度约束为vd=2 000 m/s.由于高超声速飞行器在再入过程中的机动能力有限,在多种约束下时间调节能力不大,因此飞行任务的时间约束设置较为严苛。基于制导方法[6-7]的经验,设计再入期望时间如表2所示。 表2 再入任务初始条件设置 仿真结果如图6~图11和表3所示。由表3可以看出,两种制导算法均能严格满足终端时间、射程、速度和高度约束。由图6的经度-纬度曲线可知,基于三维解析解的再入协同制导方法规划出的弹道大多沿着飞行器与目标构成的大圆弧进行运动,而本文基于纵程解析解的智能横程机动再入协同制导方法规划出来的弹道具有更大的横程机动,能够充分发挥飞行器的侧向机动能力,极大地增加了突防的成功概率。图7的高度-时间曲线与图11的弹道倾角-时间曲线显示:相比于AGCF,本文制导方法规划的高度曲线更加平滑,更容易应对较为严苛的过程约束;特别是即将命中目标的最后飞行阶段,AGCF弹道高度有明显的跳起,容易造成较大的终端高度偏差和弹道倾角误差。图8展示了速度-时间变化曲线,可以明显得看出更短的飞行时间约束会使速度减小更快。图9对比了两种再入任务的倾侧角-时间曲线,最后倾侧角大小均收敛到了0°附近。虽然基于DQN的智能横向机动决策器会在刚开始进入平稳滑翔段的时候迅速进行一次倾侧反转,但是由于训练时采样时间设置的比较大,且本文对倾侧角指令变化率进行了限幅,所以倾侧反转速率在控制系统能力允许范围内。由图9可以看出,相比于AGCF,除去飞行器由初始下降段刚开始进入平稳滑翔段时一次微小的倾侧反转,本文提出的制导方法在平稳滑翔阶段的倾侧反转次数比AGCF要少,控制更为简单,飞行器的潜在横向机动能力也得到了更大程度的开发。图10显示了两种制导方法攻角时间曲线对比图。由于两种制导方法采用的高度调整段制导策略不一致,末段攻角曲线有较大差别。AGCF末段通过调整攻角的最小值以满足高度约束,然而其弹道曲线在末段振荡较为剧烈。在末段稠密大气环境中,过大的振荡会对飞行器热控系统带来较大的压力。因此,本文则采用三维比例导引策略以满足终端高度约束,这样可以使得图7中的弹道曲线变化更加平缓。在本文中,当飞行器由平稳滑翔段过渡到高度调整段时,纵向平面内合外力不再满足平稳滑翔条件,所反求得到的攻角存在突变现象,但是通过1.2节中对攻角的变化率进行约束,可以使得攻角变化在控制系统承受范围内,满足工程实际需求。 图6 两种再入任务下不同制导方法的经度-纬度曲线对比 图7 两种再入任务下不同制导方法的高度-时间曲线对比 图8 两种再入任务下不同制导方法的速度-时间曲线对比 图9 两种再入任务下不同制导方法的倾侧角-时间曲线对比 图10 两种再入任务下不同制导方法的攻角-时间曲线对比 图11 两种再入任务下不同制导方法的弹道倾角-时间曲线对比 表3 两种再入任务下不同制导方法的仿真结果对比 在训练好的智能体基础上,改变初始发射点与期望时间约束,进行多智能体协同打击任务。3个飞行器的初始仿真设置如表4所示。 表4 多飞行器再入初始条件设置 再入初始高度为80 km.打击目标经纬度坐标为(0°,-30°)。终端射程约束Sd=50 km,终端高度约束Hd=25 km,终端速度约束vd=2 000 m/s.飞行器M1~M3的初始发射时间分别为0 s、117.7 s和204.6 s. 飞行器M1、M2、M3分别基于回报函数((34)式)中倾侧反转次数的权重ζB=10(飞行器M1、M2)和ζB=20训练得到的智能体进行制导仿真。 仿真结果如图12~图16和表5所示。由图12的经度-纬度曲线可以看出,针对不同初始点与再入时间约束,飞行器展现出不同的横向机动能力。图13为多飞行器协同打击任务的高度-能量曲线,从中可以看出过程约束均严格满足。图14为多飞行器协同打击任务的速度-时间曲线。图15中的倾侧角-时间曲线显示,相比于传统的制导律规划轨迹方法较为固定,本文提出的横向智能机动策略则更具创造性。由于设计M3飞行器回报函数时倾侧反转次数的权重ζB较大,所以飞行器能够凭借更少的倾侧反转次数命中目标,横向机动幅度更大。而飞行器M1和M2的倾侧角控制曲线显示,尽管本文在设计DQN算法时有意识地朝着减少倾侧反转次数的方向设计回报函数,但是根据不同的任务需求,制导算法可以智能调节横向机动能力,以实现终端时间约束与射程约束。图16为多飞行器协同打击任务攻角-时间曲线。表5展现了多智能体协同打击任务的状态量误差,可以看出,协同飞行时间误差控制在0.1 s以内,终端射程偏差不超过0.1 m,验证了本文提出的再入协同制导方法的有效性与准确性。综合来看,基于智能横向机动的多智能体协同制导可以通过不同横向机动形式在指定时间打击目标,极大地增加了突防成功概率,为饱和打击任务提供了可能。 图12 多飞行器协同打击任务的经度-纬度曲线 图13 多飞行器协同打击任务的高度-能量曲线 图14 多飞行器协同打击任务的速度-时间曲线 图15 多飞行器协同打击任务的倾侧角-时间曲线 图16 多飞行器协同打击任务的攻角-时间曲线 表5 多飞行器协同饱和打击任务的仿真结果 本文设计了一种基于纵程解析解的智能横程机动再入协同制导方法,可以实现高超声速飞行器协同攻击。得出主要结论如下: 1)本文制导方法的横向制导方法设计基于强化学习DQN算法。相比于AGCF,本文制导方法采用调节回报函数权重的方法,可以有效减少倾侧反转次数,使得再入飞行器在复杂任务中更大程度发挥其横程机动能力成为可能,增大了突防概率。 2)针对不同再入任务,基于DQN的横向智能决策器摆脱了原来基于规则的横向制导逻辑约束,具备自主智能调节反转策略的能力和良好的任务适应性,使得再入弹道横向设计具有更多的可能性。 3)在高度调整阶段采用三维比例导引进行设计,在严格满足终端高度约束的条件下,能够使高度曲线变化更加平缓,更易满足严苛的过程约束。 4)本文制导方法采用“离线强化学习+在线智能体应用”的模式,能够适应不同起始点、不同飞行时间约束等问题,制导精度较高,具有良好的应用前景。考虑到其优秀的横程机动能力,未来有望应用于多飞行器协同规避多禁飞区轨迹设计,进一步提高高超声速武器智能化水平。2.3 基于强化学习的横向制导方法设计
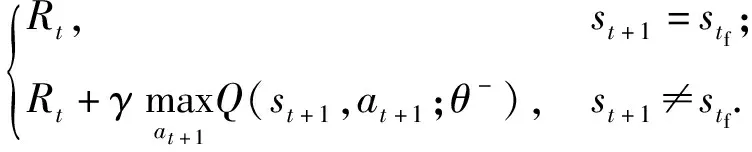
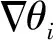
2.4 指令攻角与倾侧角设计
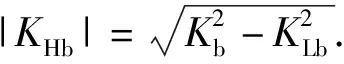
2.5 高度调整段制导方法
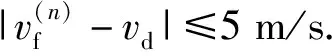
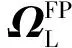
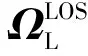
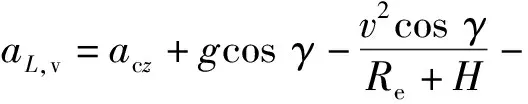
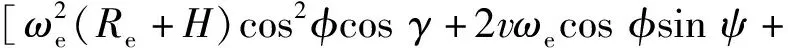
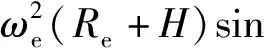
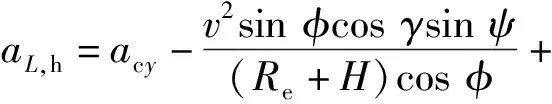
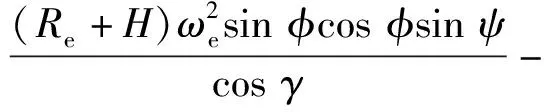
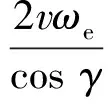
3 仿真验证
3.1 与基于三维解析解再入协同制导方法对比仿真
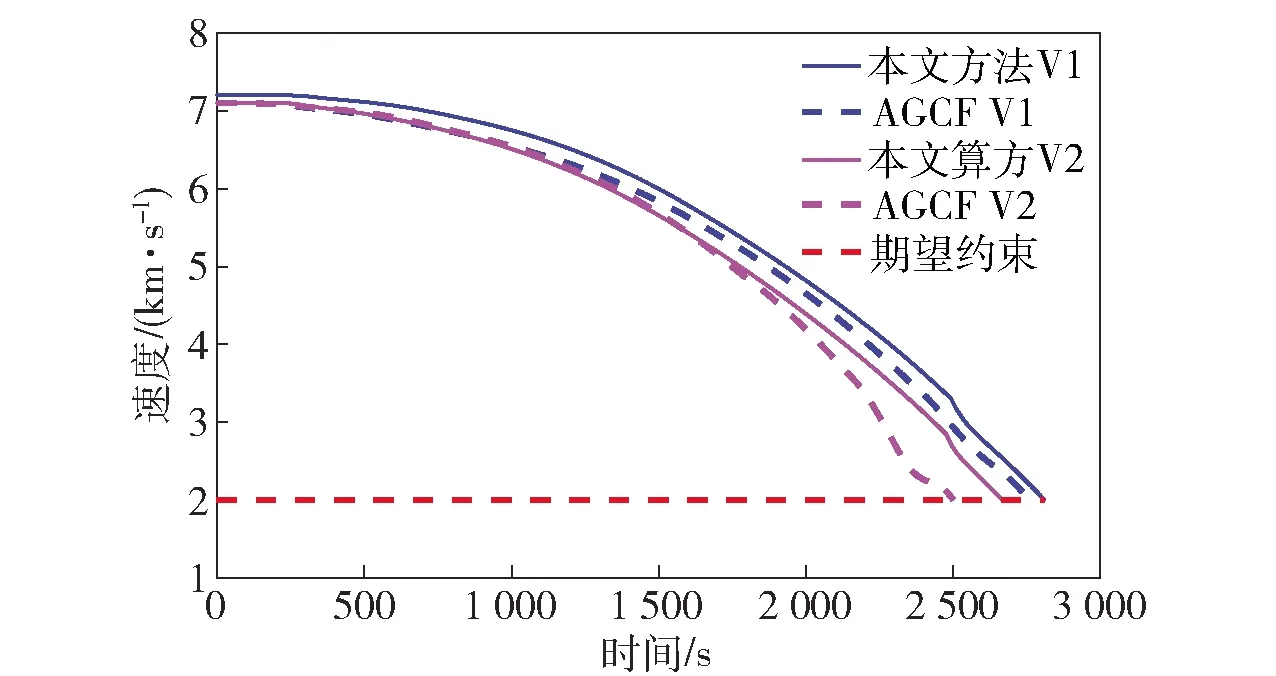
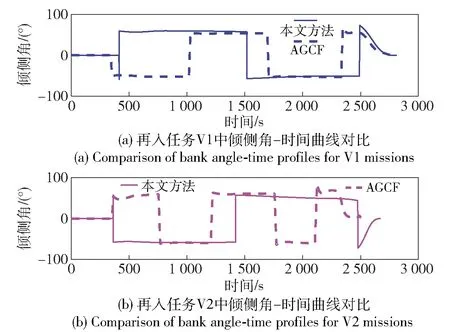
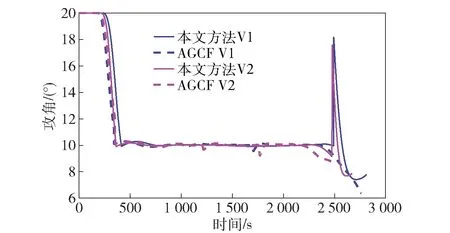
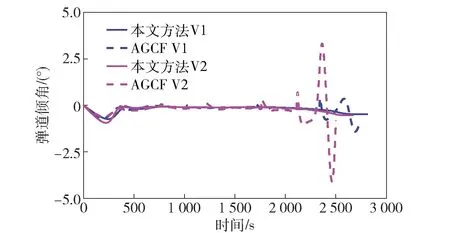

3.2 多智能体协同打击仿真
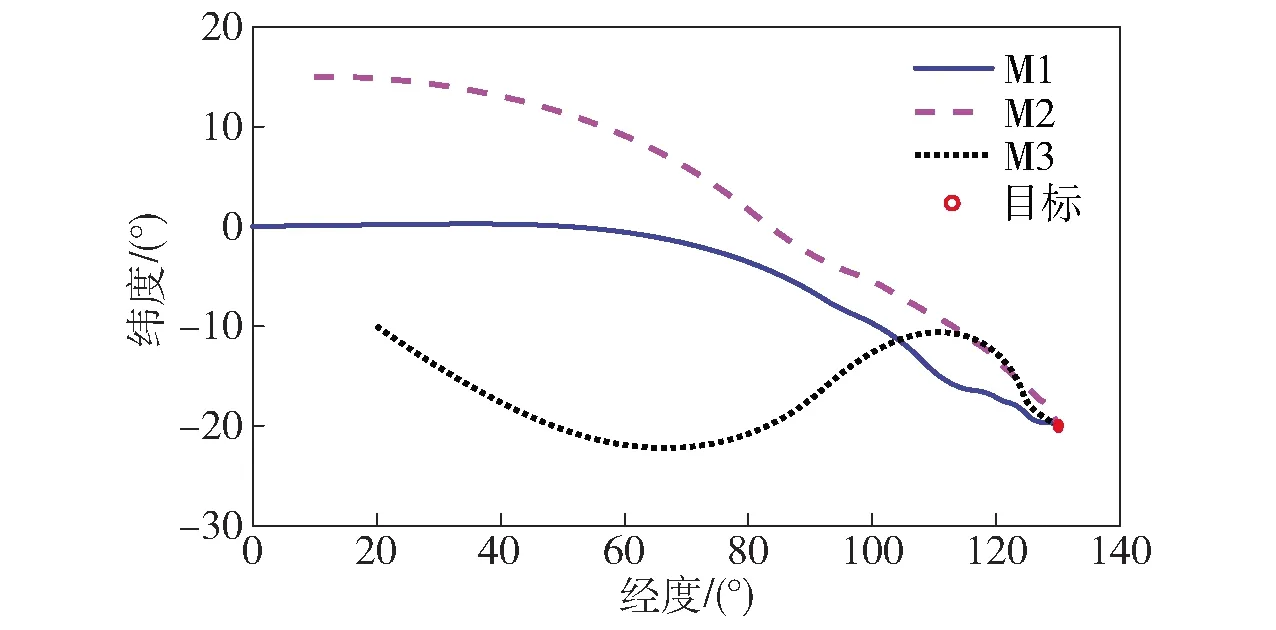
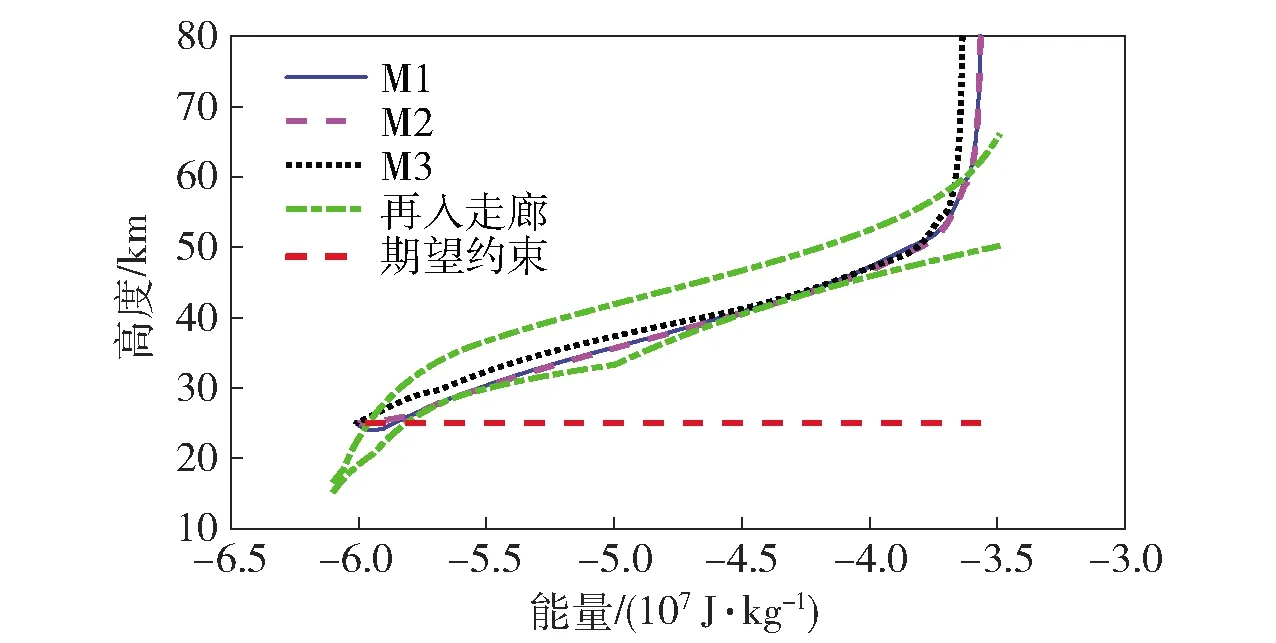
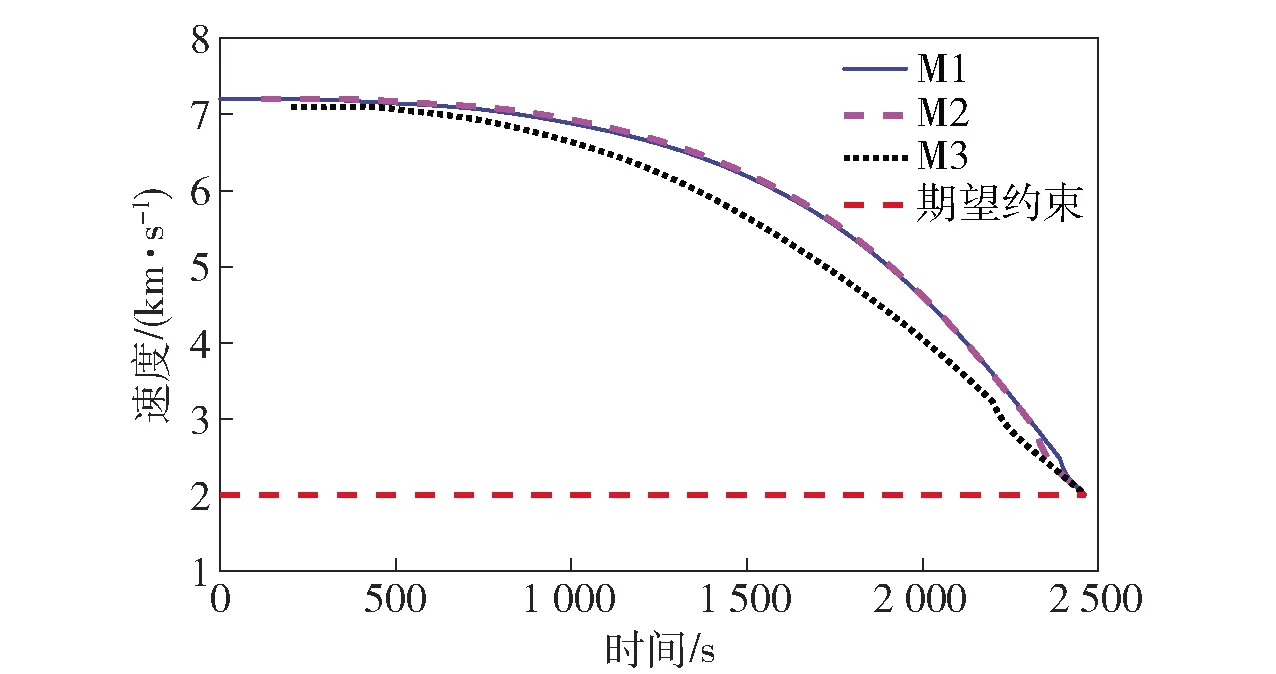

4 结论
