浅谈在混合式课堂教学中培育中职生数学核心素养

嵇珍妮

[摘           要]  随着新课标及中职数学教学改革的发展，职业学校数学课堂多采用线上线下混合式教学，旨在培养学生的数学核心素养。在课堂教学中，遵循学生的思维认知规律及参差不齐的知识水平，充分利用数学软件及教学平台，经历作图、操作实验、数学计算、直观感受、抽象分析、小组合作等学习活动，帮助学生建立直观想象、数学运算的方法策略和思维习惯，从而培育学生的数学核心素养。

[关    键   词]  数学核心素养;混合式课堂教学;中职生

[中图分类号]  G715                   [文獻标志码]  A                      [文章编号]  2096-0603（2021）21-0038-02

随着新课标及中职数学教学改革的发展，职业学校数学课堂多采用线上线下混合式教学，旨在培育学生的数学核心素养。大多数中职生是初中毕业且学习习惯和态度不好的青少年，到了中职学校，他们总觉得学数学理论知识对将来就业没有任何用处。事实上，开设数学课程的目的除了让学生在学习过程中获得学习和职业发展所必需的数学知识、技能、方法之外，更重要的是让他们形成理性思维去面对人生的各种问题，在继续学习和未来的生活工作中运用数学的思想方法和工具解决问题，具备一定的工匠精神，养成良好的道德品质，从而逐步形成正确的价值观念、必备品格。

《中等职业学校数学课程标准》指出，数学学科核心素养包括数学运算、直观想象、逻辑推理、数学抽象、数据分析和数学建模。混合式课堂教学我们一般采取的方法是：课前，教师备课同时确定本节的重难点，并将本节的重难点以微课形式呈现在教学平台上，学生在平台上自主学习本课知识点，小组合作探讨，完成教师发布的任务点。在这个学习过程中，学生逐渐形成了小组合作、逻辑推理、数据分析这些核心素养，在将来的生活工作中定会受益匪浅。课中，教师首先点评学生课前任务完成情况，并邀请学生相互点评，然后将新课的知识点设置情境导入、做中学、做游戏、运用手机数学软件辅助学习等学习方式，调动学生学习的积极性和参与度。课后设置不同层次的练习题，给予学生选择答题的机会，旨在培养他们想学知识、要学知识、学会知识，应用能力得到提高等核心素养。笔者已开设的校级公开课“二元线性规划问题的图解法”一课为例，谈谈如何在中职混合式课堂教学中进行数学核心素养的培育。

一、本节课教学设计思路说明及课堂实况

（一）内容选定，设置情境导入

从平台中调出学生课前任务——如何画出不等式组所表示的平面区域的完成情况，教师点评，学生相互点评。接着提问什么叫可行域、可行解以及最优解。根据学生的回答，老师直接在电子白板上用彩色笔标出并深层次解释这几个概念，以帮助部分没预习或者不能理解概念的学生。

师：同学们，在日常生活中，我们经常遇到这样的问题：如何合理利用人力、物力等资源得到最大的经济效益，我们需要从这些问题的可行性解决方案中选择一个最优的方案。今天我们一起学习一种办法——二元线性规划问题的图解法来寻求最优方案。

【设计意图】（1）点评学生作业，旨在检测学生课前对概念的预习与理解情况，培养中职生自主学习的能力。（2）学生已经初步学会根据实际问题建立数学模型，能画出不等式组所表示的平面区域，知道了可行域、可行解及最优解概念，那么如何去求目标函数的最优解呢？这正是本节课所要解决的问题，具备知识的连贯性，也激发了学生的学习兴趣和好奇心。

（二）任务导学，小组合作，再研共研

首先，PPT呈现任务一：两个探究，学生分组，每两个学生共用一部平板电脑合作探究。

探究一 在平面直角坐标系中，Ax+By+C=0（A，B不全为0）表示一条直线，那么当C取不同的值时，所得的直线具有什么关系呢？

探究二 将直线Ax+By=0（A>0，B>0）往其上下平移时，观察z=Ax+By的值的变化情况。

师：请一位同学到黑板上给我们汇报展示一下成果。

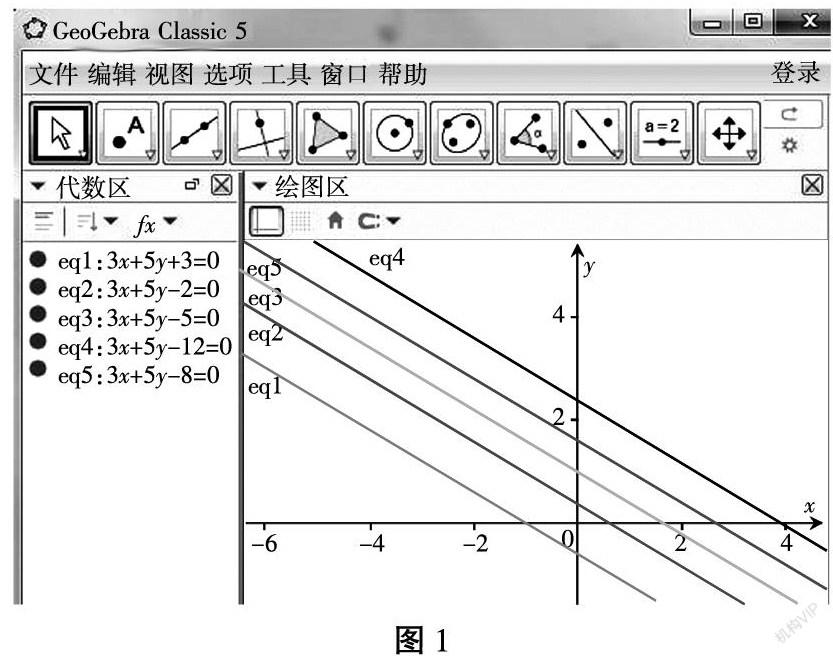
生：首先我画3x+5y+3=0，3x+5y-2=0，3x+5y-5=0等这些直线，观察发现这些直线都是平行的关系（如图1）。其次我作直线3x+5y=0，当我将该直线往上平移时，z的值在增大;当直线往下平移时，z的值在减小（如图2）。

【设计意图】抛出任务，学生分小组合作探究，自己动手画一画，借助数学软件，直观形象，将难点简单化，同时学生动手操作数学软件、看图观察分析、概括语言等核心素养得到很好的培育;直观易懂，让学生品尝到学习数学的乐趣。

其次，PPT呈现任务二，让学生交流研讨。

各小组交流热烈，有的学生借助软件直接得到答案，但是有些困惑，有的学生在纸上手动作图。

师：请大家看一下你们作出的可行域是否正确。那么你们将目标函数平移时，发现在什么地方取得最大值呢？哪个小组愿意上来跟我们分享成果？

生：可行域没错，当目标函数移到3x+4y=250与2x+y=100这两条直线的交点的地方，取最大值。

学生讲解得就像个小老师，自信满满，表达比较清楚，其余小组似乎得到了同样结论。

师：同学们很喜欢这个软件作图，既快又准确，下面要求大家自己在做学案上作出可行域和目标函数，然后自己用道具移一移，算出交点坐标及最优解。