MOTOMANGP180型工业机器人的建模与仿真研究*

刘晓刚，吴俊辰，孙 红，陈志峰，郑利华

（1.广西科技大学机械与交通工程学院，广西柳州 545000；2.桂林航天工业学院汽车与交通工程学院，广西桂林 541000）

0 引言

在工业自动化技术高速发展的今天，机器人被广泛用于各种重复性高、危险系数大的工作场合来代替人工进行操作，实践证明，工业机器人可以在质和量的基础上提高市场竞争力。与此同时，在确保人身安全、降低成本、改善工作环境、减少人体劳动强度、提高劳动生产效率等方面也具有十分重要的意义。为研究工业机器人在实际中的应用，首先得对机器人进行动力学分析，得到机器人各个连杆的位置与末端执行机构的位置关系，再根据给定的位置要求进行机器人的控制。

MatlabRoboticsTool 是由澳大利亚科学家Peter Corke 开发的机器人运动学分析与仿真的程序，已被广泛运用于机器人运动学分析、动力学分析、轨迹规划等研究。如房炜[1]利用该程序在关节空间对三次多项式插值、五次多项式插值以及“353”多项式插值进行了阐述与仿真，结果验证了在关节空间采用高低次结合的多项式插值优于单一多项式插值。沈冬冬[2]运用5次多项式拟合关节位移变化轨迹；最后采用二分法求解满足各关节速度约束和力（矩）约束的最优运动时间，从而生成各关节运动轨迹，并且进行了对比实验。通过机器人工具箱生成的数据表明，该轨迹规划方法能有效地缩短冲压机器人的工作周期。针对安川生产的GP180 型工业机器人，目前基本没有人进行过正逆运动学仿真与轨迹规划一个完整体系的仿真研究，本文对GP180 型的机器人进行运动学与轨迹规划方面的研究，为今后该机型的研究提供思路。

1 机器人建模

根据官网MOTOMAN－GP180 型机器人的参数可知，GP180 为6 自由度垂直多关节型机器人，最大载重为180 kg，重复定位精度为±0.2 mm，6 个关节均为旋转关节，S、L、U三轴控制整个机器人的位置，R、B、T 三轴控制末端手腕的姿态，并且这三轴轴线相交，符合Piper[3]准则。机器人本体标准规格如图1所示，GP180几何参数如图2所示。

图1 机器人本体标准规格

图2 GP180几何参数

采用标准DH[4]参数法，建立DH坐标系如图3所示，以基座旋转轴为1号轴，依次对旋转轴进行编号，建立六连杆坐标系模型。对于6个关节均是由电机驱动的旋转轴而言，旋转轴即为Z轴。当两相邻Z轴相交于一点（ai＝0），X轴在与两Z轴都垂直的直线上，若相邻两Z轴不相交（ai≠0），则X轴沿着ai方向，由Zi-1指向Zi。最后根据右手定则确定Y轴的方向。最后，根据右手旋转准则确定各个坐标系Y 轴的方向[5]。

图3 GP180机器人连杆坐标系模型

根据标准D－H参数法的定义，连杆长度为ai，表示沿着Xi方向Zi与Zi+1的距离；从Xi的方向看，Zi与Zi+1之间的夹角为αi，设两连杆偏距为di，即表示相邻两Xi-1轴与Xi轴在Zi-1轴方向上的距离；关节转角为θi，即连杆i－1与连杆i绕Zi-1轴的转角。其具体参数表示如表1所示。

表1 GP180 DH参数表

2 运动学方程

根据标准D－H 参数法坐标系中相邻坐标系变换矩阵通式：

将θ、d、a、α等参数代入通式，为节约篇幅，用ci代表cosθi，si代表sinθi，i＝1，2，3，4，5，6（以下同）。可得：

根据连乘法，可以得到正运动学方程为：

3 建立仿真模型

在Matlab2019a的环境下利用Peter Corke[6]开发的机器人运动学分析与仿真的程序Robotis Toolbox 9.1.0，对机器人进行建模。先利用“startup”指令启动Robotics Toolbox，再利用Seri⁃alLink指令进行模型的建立。

运行该程序后，在Matlab中生成“MOTOMAN GP180”仿真模型如图4所示。

图4 MOTOMAN GP180三维模型

3.1 正运动学分析

工业机器人运动学研究的是工业机器人的关节角信息与工业机器人位姿矩阵间的对应关系，将关节角转换为位姿矩阵的运算称为正运动学，反之将位姿矩阵转换为关节角的运算称为逆运动学。针对6个自由度均为旋转的机器人而言，逆解可能存在多种情况，经过多次数据比对，将6个关节的转角均设为30°，选择最优解。使用Fkine 指令对机器人进行正运动学求解，程序如下：

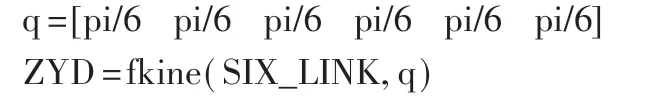
得到正运动的位置矩阵为：

根据正运动学计算公式，可计算出机器人位置矩阵：

计算结果与MATLAB程序Fkine指令运行结果一致。

3.2 逆运动学分析

MOTOMAN GP180的最后3个旋转轴的中心线彼此垂直并且3个轴在同一点相交，符合Pieper准则，故存在封闭解。本文采用矩阵逆乘的方法来求解，对公式（2）两边求逆可得：

公式两端对应元素相等，可以得出：

θ1＝arctan 2(py,px)或arctan 2(－py,－px)，其他5 个角度依次类推，进行变化逆矩阵等运算得出，本文不一一列出，详细步骤可见文献[7]。通过矩阵逆乘的方式得到6 个关节角的全部解，可由最终计算式可知θ1、θ2、θ3只含有px、py、pz3项，这3个参数在旋转变换矩阵中决定着末端执行器的位置，而θ4、θ5、θ6只含有变换矩阵中决定末端执行器的姿态参数nx、ny、nz、ox、oy、oz、ax、ay、az，根 据MOTOMAN GP1806个关节的特性，可初步判断逆解的正确性[8]。

3.3 工作空间分析

在Matlab 软件中，根据6 个关节角的角度范围和位置方程，应用蒙特卡洛法[9]，输入如图5所示的程序，工作随机点选择10 万个，最终生成的工作空间图如图6～9 所示，分布点较为密集，无明显间隙，能够满足该范围内的工作要求。

图5 蒙特卡洛法代码

图6 三维工作空间图

图7 XOY工作空间

图8 XOZ工作空间

图9 YOZ工作空间

4 GP180运动轨迹规划

针对 GP180 的运动，选定初始位置点为[0 0 0 0 0 0]，末端位置点为[π/4,－π/3,π/5,π/2,－π/4,π/6 ]，轨迹规划方法选择五次多项式插值函数，即JTRAJ 函数，表达式为：

其约束条件为：

简化得到的解为：

利用Matlab调用Plotq函数进行轨迹模拟可得到图10所示的曲线图，可以看出6个关节的位置曲线均连续，未出现明显波动。

图10 关节位置曲线

同理，调用Plotqd与Qdd函数绘制出6个关节的速度与加速度曲线如图11～12所示，均为连续无波动的曲线。

图11 各关节速度曲线

图12 各关节加速度曲线

将各关节运动代码进行整合并运行，可得到机器人最终姿态与各个关节在同一时间的运动状态如图13所示。

图13 各关节位置、速度、加速度运动曲线

5 结束语

对于安川生产的GP180 型工业机器人，利用标准D－H 法来建立模型，对相邻坐标系间的变化进行计算推导，6轴之间的变换矩阵连乘可得到正运动学方程，利用Matlab 里的机器人工具箱建立仿真模型，模型中的姿态与实体一致，另给定角度运用Fkine函数对机器人位姿进行求解，与公式计算结果一致，证明模型建立正确。采用蒙特卡洛法对机器人工作空间进行模拟，得到的点图可知机器人工作范围满足大多数工作要求，最后利用JTRAJ 函数对机器人进行点到点的路径规划，得到的位置、速度、加速度曲线均连续，无明显波动，为该机型工业机器人的后续研究提供了参考。