弱客流地区客货共享定制公交路线的动态规划方法

柏海舰，汪 俊，钟剑锋，卫立阳

(合肥工业大学 汽车与交通工程学院，安徽 合肥 230009)

0 引 言

将客运需求与货运需求进行联合运输能在减少资源使用的同时提高运行效益。针对不同的运输环境，客货联运模式已衍生出多种类型。

A. TRENTINI等[2]构建了一个共享旅客和货物流之间的运输资源运输模型，将客运和货运流量整合到现有城市交通系统中，并对此种重叠进行表征，即将两种流量进行量化。为了解决两层交通问题，R. MASSON等[2]创建了一个数学模型及一个自适应大邻域搜索算法。在第一层，货物在城市公交车中从配送中心运输到一组公交车站，主要思想是利用公交车的剩余容量将货物运送到市中心；在第二层中，最终货物由接近零排放的城市货运船队分配。E. FATNASSI等[3]为了研究在城市地区整合共享商品和按需乘客快速运输系统的潜力，基于个人快速运输和货运快速运输的共同特点，提出了一种快速有效的运输解决方案，来提高城市物流的可持续性。贺韵竹等[4]以最优的快递运输总成本为目标，构建了一种自营货车与公交车协同配送的优化模型。为解决带有时间窗和计划线路的接送问题，V. GHILAS等[5]提出了一种自适应大邻域搜索启发式算法(ALNS)。该算法有效地考虑了固定线路的时间表、同步与时间窗口约束等复杂方面。大量计算实验的结果表明，ALNS在生成的PDPTW-SL(带有时间窗和预定线路的取货和交货问题)实例上找到高质量的解决方案非常有效，该实例具有多达100个合理代表现实生活情况的货运请求。货物运输对于城市和地区的经济增长至关重要,A.MUOZ-VILLAMIZAR等[6]提出了一种使用OEE(总体设备有效性)度量标准来评估城市货运系统有效性的新方法，OEE度量标准是精益制造框架中使用的众所周知的比率。该方法使用具有几个目标函数的数学模型来探索经济发展、质量、绩效和可利用性(OEE的部分利率)之间的关系和权衡，最终目标是优化OEE指标和运输系统的盈利能力。

在乘车需求分布广且需求密度低的弱客流地区，客运车辆的载客率往往较低，若在弱客流地区进行客货联运，将能提高车辆的使用效率，减少车辆使用数。

笔者提出的运输模型对弱客流地区出现的客货运输需求进行车辆安排与线路规划。笔者首先为场景建模，对不同类型的运输需求建立线路生成规则，然后通过算例来证明系统的可行性并比较在相同运输需求与运行环境下，采用混合运输与不采用混合运输这两类模式所需的车辆数以及线路情况。

1 系统搭建

1.1 场景描述与运行流程

运输系统在发车前会根据提前收到的乘车需求对该班次的车辆数与线路进行规划，使得运输需求在规定的时间窗内完成，同时应满足一些优化目标，如系统总体运行时间最小或运行成本最低等。系统总体运行结构如图1。

图1 系统总体运行流程Fig. 1 Overall system operation process

车辆与线路初始化完成后，系统开始运行，若运行时出现动态运输需求，在使车辆原运输需求的时间窗依旧满足及车辆容量允许的条件下，可将动态需求插入到车辆运输线路中去。

该系统运行前需要知晓各站点之间的连通性及各站点之间的最短路径和距离。

在笔者的客货共享的运输模式中，车辆按班次发车，乘客与货物的运输需求分为动态需求与静态需求。车辆在运行时出现的乘车需求定为动态需求，车辆发车前收集到的乘车需求为本班次的静态需求，该班次无法满足的动态需求会划归到下一班次的静态需求中。

运行时，车辆从起始点出发，途径各个需求起始点，最终到达终点站。车辆能容纳的最大客货量分别为Q与Qh。发车前根据收集到的静态需求生初始线路，并在车辆运行时，根据动态需求的信息在考虑初始乘客和动态需求的时间窗约束下，进行路线动态规划。

1.2 初始路线生成

将上一班次运行时出现的、未被满足的动态运输需求以及上一班次结束后出现的运输需求定为下一班次的静态运输需求。在笔者构建的运行模型下，乘客与货物需提前向系统提交自己的运输需求，需求信息应包含需求的起始站点，客货各自期待被接送的时间窗(e,l)与(eh,lh)，需求的大小qh与qkh以及各自能够接受的最迟送达时刻lj与ljh。当车辆在期望送达时间窗前到达需求站点时，车辆需要进行等待,总等待时间记为TW，直至到达时刻e或eh。

以系统中静态需求规划生成的车辆线路应当满足约束：①minαTH+βKT；②maxTA。其中：TA为线路余度，反映的是线路的可插入度；TH,TK为系统中一个班次车辆总的货运时间与总的客运时间；α,β为车辆货运总时间与客运总时间各自所占的权重，可人为调节。其中：

(1)

s.t.

(2)

(3)

ti≤li

(4)

tih≤lih

(5)

tij≤lij

(6)

tijh≤lijh

(7)

(8)

(9)

在时间窗之前到站的车辆需要进行等待，直至时间窗起点时刻。

约束条件可分为4大类：式(2)、式(3)为车辆容量约束，即在车辆运行的各个时刻，在线客运需求与货运需求均不可超过车辆的客容量与货容量上限；式(4)～式(7)为时间窗约束，即车辆需要在需求提交的时间窗前或时间窗内完成需求的接送任务；式(8)为车辆数约束，即出发车辆数与最终到站车辆数目应相同，一个班次内从始发点出发的车辆数与到达终点站的车辆数相同；式(9)为防止运输线路出现子回路的约束。

当所有仅在站点连通度上可行的线路生成后，再使用约束条件进行挑选，生成满足约束的线路，最后选出线路余度最大的线路作为最终的车辆行驶线路。线路生成应以最小化客货运的等待时间为首要目标，在等待时间相同的情况下，尽可能提高线路余度TA。

静态需求的线路规划以最小化乘客与货物的运行时间为目标，通常货物对于运输时间的耐受度要强于乘客，所以可以适当调高α值。

1.3 路线的动态规划

车辆在运行过程中，会有新的运输需求出现。同样，新的运输需求需要提交的信息包含起始站点、客货各自期待被接送的时间窗(e,l)与(eh,lh)、需求大小以及各自能够接受的最迟送达时刻lj与ljh。系统会对这些需求进行判断，符合插入条件的运输需求会插入正在运行的车辆线路中；对于不符合插入条件的运输需求，将其归纳到下一班次的静态需求中进行规划。

新需求在插入时应考虑原有已规划好需求，在满足原有需求的时间窗约束与车辆的容量约束的条件下，插入需求后生成的新线路尽可能提高系统的服务水平以原有乘车需求的满意度。

插入动态需求时的目标函数以约束条件与静态需求相同，插入动态需求的新线路仍要对线路的余度进行比较，以提高后续出现的动态需求的可插入性。

线路的余度大小反应了线路的可调整性。当在系统运行时会出现动态的运输需求，当车辆响应这些需求的时候，需要对原始的线路进行调整。线路的余度越大，留给动态需求的调整空间就越大，动态需求也就越有可能被接受。

当车辆的线路确定后，站点的到达顺序亦随之确定。由于每个需求均包含期望接到的时间窗以及最迟被送达时刻，所以两相邻站点之间存在一定的松弛时间，松弛时间的大小代表了站点间对于新需求的接收程度。站点间的松弛时间计算如式(10)、式(11)：

(10)

(11)

式中：L代表两站点间的最短路径距离；V代表车辆速度；e与l分别代表后一站点的期望最迟送达时间与前一站点的期望最早到达时间；l′为当前一站点为需求起点时前一站点的期望最迟送达时间。采用TS1计算站点间的松弛时间。当前一站点为需求终点时，采用TS2计算站点间的松弛时间。

由于松弛时间具有后向传播性，即在线路中靠前的站点插入动态需求所产生的延迟时间会对后续的站点产生影响。

产生影响的只有后向站点，不会对前向站点产生影响，如图2。所以对于各个站点而言，最大余度为其前所有站点中最短的站点松弛时间。对应整体线路而言，线路的最大余度为所有站点松弛时间的最小值。即：

图2 需求插入后的延迟传播Fig. 2 Delayed propagation after demand insertion

TA=min(TS1,TS2,…,TSi) (i=N)

(12)

2 算法设计

系统准备发车前，依据静态运输需求，开始初始车辆数以及各个车辆的线路确定，具体流程如图3。

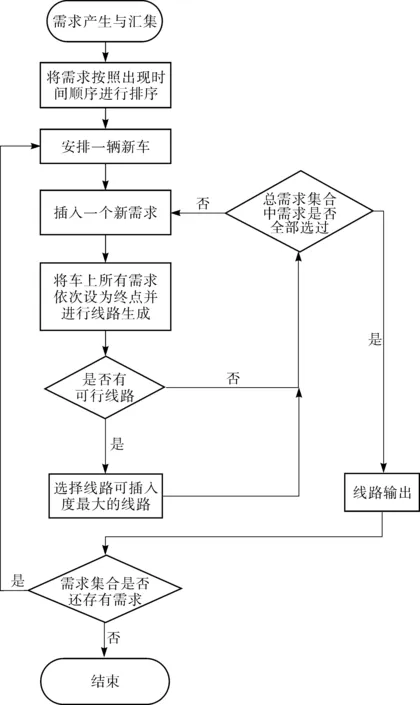
图3 初始路线生成流程Fig. 3 Initial route generation flowchart

Step 1将需求集合中最早出现的需求放入车辆中，并通过将车上所有需求依次设为终点，采用深度优先加回溯的方法生成线路。

Step 2判断是否存有可行线路。若有可行线路，选择线路余度最大的作为最优解，同时将该需求从需求集合中去除，再次进行Step 1操作；若无可行线路，选择需求集合中后一需求进行插入操作，若无可行线路继续进行该步骤，直至所有需求全部被选择过。

Step 3判断需求集合中是否还有存有需求。若有，则增添一辆新车，继续从Step 1开始产生线路;若无需求，则线路生成与车辆的数目确定就此结束。

Step 1中采用深度优先加回溯的方法[7]，生成不考虑约束条件下的所有可行线路。该算法在图论中可用于搜索两点之间的所有可行线路，笔者采用该算法计算出依次以所有站点为终点的所有可行线路，此可行性仅为站点连通性方面的可行性。

M. BARKAOUI等[8]使用遗传算法的自适应进化方法，解决在带时间窗的动态车辆路径与遗传算法收敛过程的策略选择和运算符的组合问题；M. DIANA等[9]提出了一种并行后悔插入启发式方法，以解决带有时间窗的需求插入问题并实施了新的路线初始化过程，该过程同时考虑了问题的空间和时间方面，然后执行后悔插入以服务其余的请求；LUO Ying 等[10]针对静态多车辆“搭便车”问题提出了一种新的启发式方法，称之为拒绝重新插入启发式方法，其主要目标是在服务质量约束下，尽量减少用于满足所有需求的车辆数量。

笔者采用2-opt的方法对线路进行扰动以产生新线路。当动态需求出现后，依据流程(图4)进行需求的可插入性判断以及新线路的生成。其中，线路的扰动采用2-opt的方法，其最早由文献[11]提出。该方法属于局部搜索算法，可用于解决TSP问题，其基本思想是随机取两个节点，对线路进行交换优化，一直到无法优化为止。

图4 路线的动态规划流程Fig. 4 Dynamic planning flow chart of route

Step 1动态需求产生后首先将其起终点就近插入到车辆的运行线路中，如图5。在将站点插入之后对线路进行扰动以产生新的线路，再对新的线路进行判定是否可行，若可行，记录并存储。

图5 动态需求就近插入Fig. 5 Dynamic demand insertion nearby

Step 2将需求点插入线路中次近的位置中，继续进行线路的扰动，存储可行线路，直至线路中所有的位置都被插入过。

Step 3换一辆车继续进行Step 1和Step 2的评估。

Step 4将所有可行线路进行比较，选择最优的线路作为最终的线路。

Step 5若所有情况下均无可行线路，则将该需求归纳为下一班次的静态需求。

文献[12]提出了一种可快速生成可行线路的2-opt 方法，采用该方法会产生与原始线路上下需求站点顺序不同的线路，如图6。

图6 2-opt产生新线路Fig. 6 New lines generated by 2-opt

图6中，圆圈内数字及字母为站点号，0号站点代表车辆的起始点，+1、+2等代表第几号运输需求上车，-1、-2等代表第几号运输需求下车。S—1—2—3—4—5—6—7—8—9—10—E为车辆初始线路。在选择了3—4和5—6两对站点作为交换起终点后，车辆行驶线路变为S—1—2—3—5—4—6—7—8—9—10—E。由于线路存在约束，在线路中进行2-opt的时候，会产生不可行的线路，因此每当新线路生成后，需要对其可行性进行检验。

一条原始线路在插入新的运输需求后会有多种扰动产生的新线路，依次检验可行性会耗费大量时间。文献[11]提出了一种通过缩小可行线路范围而减少验证时间的方法。通过该方法可找到潜在可行的线路交换起始点，具体如表1。

表1 站点i与FD(i)值Table 1 Station i and FD (i) values

表1中：i为原始线路中的站点号；FD(i)为从第i号及其以后站点上车需求的第1个下客站点号，如FD(3)=5代表了从原线路第3号及其以后站点上车需求的最先下客点为5号站点。

可将第i个站点设为扰动出点，FD(i)为扰动线路的入点，第i+1号站点为第2段的出点，FD(i)+1为第2段的入点。例如以第5号站点为扰动出点，FD(5)=7，第7号站点为扰动线路的入点，第6号站点为第2段的出点，FD(5)+1=8，第8号站点为第2段的入点，如图7。

图7 新的可行路Fig. 7 New feasible road

新线路为S—1—2—3—4—5—7—6—8—9—10—E，在运输需求起终点顺序上可行，下一步即可开始约束条件的检验。

通过该扰动方法并不一定能完全能生成满足运输需求起终点顺序的新线路，但可缩减新可行线路的生成时间。

3 算例分析

3.1 可行性检验

为验证笔者提出的客货混运模型的可行性，笔者进行算例计算。随机生成运输路网，结构如图8。

图8 算例路网Fig. 8 Example road network

在运行系统中，生成各个直连站点间的距离。假设车辆行驶速度恒定，根据路网站点间的连通性，用直连站点间的行驶时间表示距离。

表2中，S为车辆发车起点，E为车辆到达终点。在此算例中，设定初始静态运输需求为 6 个，动态运输需求数为 4 个，设车辆的可载客运需求量为 3，可载货运需求量为 2。记系统中，该班次发车时刻为 0 时。运输静态需求如表3。

表2 直连站点的时间距Table 2 Time interval of directly connected stations min

表3 静态运输需求Table 3 Static transportation requirements

运输动态需求如表4。

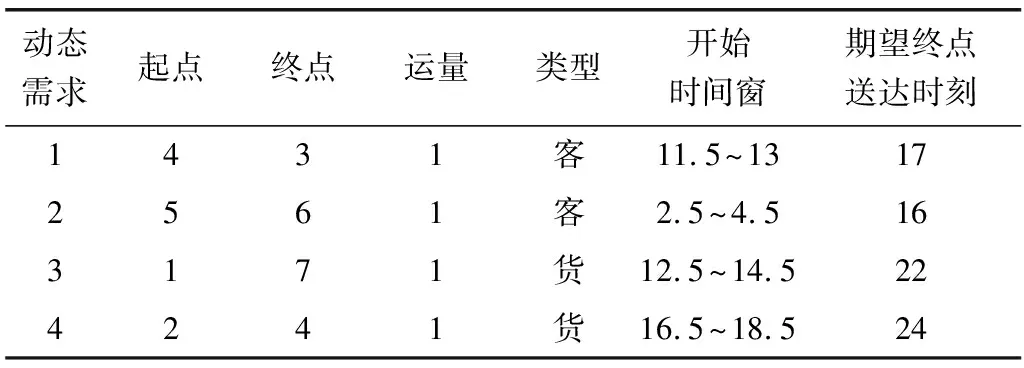
表4 动态运输需求Table 4 Dynamic transportation requirements

按静态需求的车辆线路生成流程图，对表3的静态需求进行线路生成，结果如表5。

表5 初始运行线路Table 5 Initial operation route

由表5可知，车辆无法满足1号动态运输需求，归纳到下一班次的静态需求中去。车辆行驶轨迹如图9。

图9 初始线路车辆线路Fig. 9 Vehicle route of the initial line

按动态需求的车辆线路生成流程，对表4的动态需求进行线路生成，结果如表6。

表6 插入动态续需求后的新线路Table 6 New lines after inserting dynamic renewal requirements

由表6可知，车辆无法满足1号动态运输需求，归纳到下一班次的静态需求中去。车辆行驶轨迹如图10。

图10 再规划后车辆路线Fig. 10 Vehicle route after re-planning

以此，算例证明了该模型的可行性。

3.2 对比分析

为对比混合运输模型与非混合运输模型之间的差异，将两类模型进行对比实验。表7、表8生成了非混合运输时的静态需求车辆路径与动态需求产生后的车辆路径。

表7 非混合运输模型的静态需求路径Table 7 Static demand path of non-mixed transportation model

表8 非混合运输模型的动态需求路径Table 8 Dynamic demand path of non-mixed transportation model

由表8可知，动态需求3、4因为时间窗约束无法被满足，划归到下一班次的静态需求中去。现将两种运输模型的车辆运行时间以及车辆空驶时间进行比较，如图11～12。

图11 不同模式下车辆线路参数Fig. 11 Vehicle line parameters in different modes

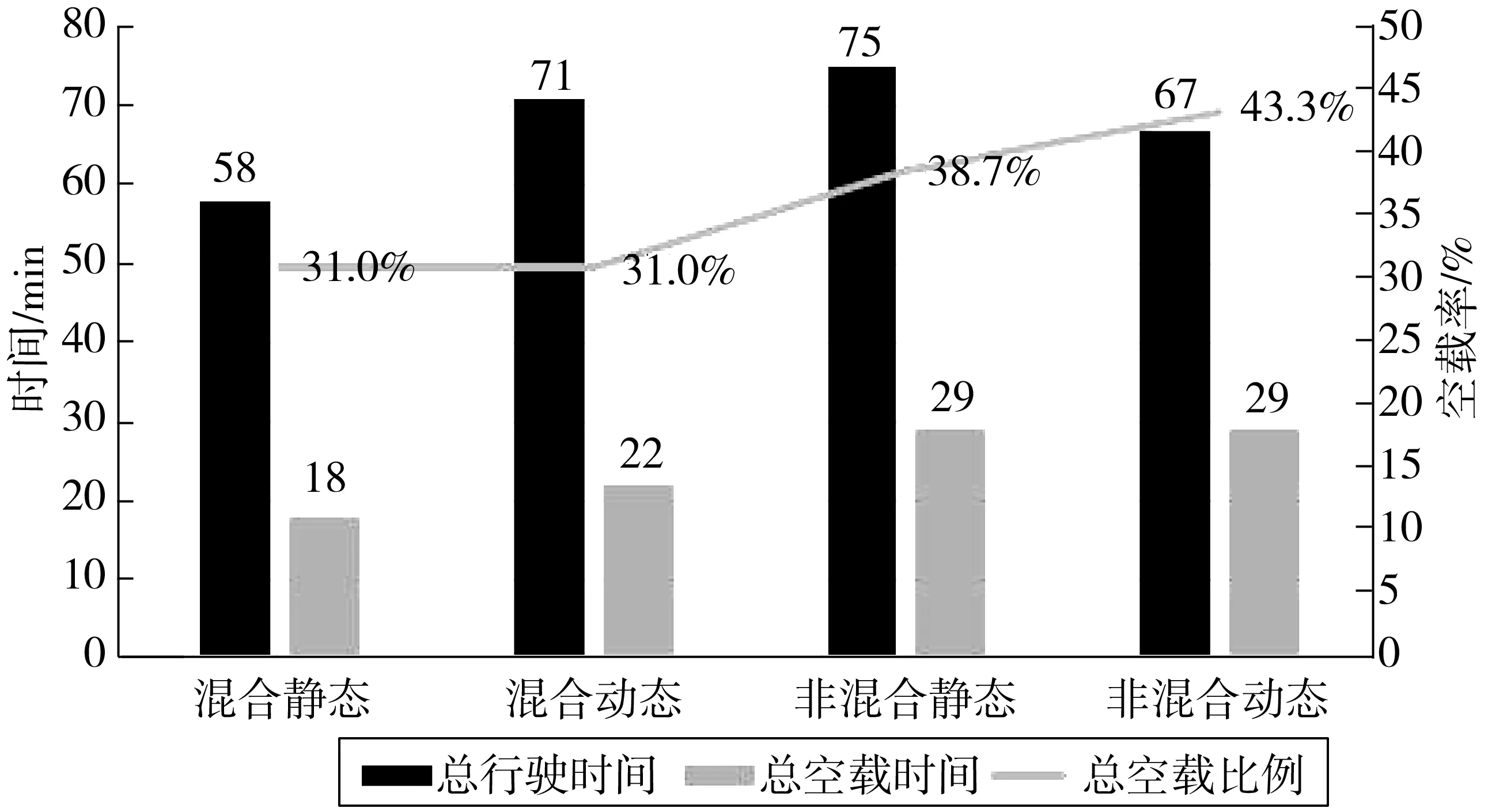
图12 两种运输模式总体比较Fig. 12 Overall comparison of two transportation modes

由图11～12可知，在相同的运输需求条件下，混合运输模型所需的车辆数、总空载时间即总空载里程数要小于非混合运输模型情况下的相应值，混合运输模型下车辆的空载率要小于非混合运输模型情况下的空载率。

4 总结与展望

1)笔者构建了一种弱客流环境下的客货混合运输模型，该模型能实时响应系统中出现的动态需求。基于算例验证了该模型的可行性。在相同运输需求下，对比了混合运输模式与非混合运输的运行情况，发现在混合运输时所需的运行车辆数较少，并对动态运输需求的满足率较高，同时车辆的空载率小于非混合运输时的车辆空载率。混合运输可降低整体的运输成本。

2)笔者将发车班次间隔设为定值，但为贴切现实应根据静态需求的情况进行调整。同时在验证可行性时，将车辆速度设为定值，为贴切现实车辆的运行情况，应当将速度设为与运行时间、路段拥堵情况等相关的动值，故而还需进行深入研究。