基于层次分析法与灰色关联度的铁路货车零部件重要度评价方法

边志宏，赵娴雅，史红梅

(1. 神华铁路装备有限责任公司，北京 100120; 2. 北京交通大学 机械与电子控制工程学院，北京 100044)

随着我国铁路建设的快速发展，对铁路货车的维修效率、经济性提出了更高的要求。构建评价铁路货车状态的指标体系，有助于建立车列健康诊断模型，实现对铁路货车健康状态的诊断，从而实现对故障的精准维修。

层次分析法(Analytic Hierarchy Process, 简称AHP)由美国运筹学家T.L.Saaty提出，该方法基于矩阵特征值的思想，实现对企业质量、机械总体性评估等方面的评价[1]。它在主观赋权的基础上，经过数学计算得出各指标的权重，能够在结合专家经验的同时，降低主观因素的影响，做出相对准确的判断。因此，可将层次分析法用于评定铁路货车零部件的重要度。但由于铁路货车零部件众多，且零部件间存在相互关联和制约的因素，目前对于铁路货车零部件尚没有成熟的评价方法。若仅采用层次分析法，存在权重选取主观性过强、缺乏科学有效的方法解决评价指标间的随机性问题，很难客观准确地进行分析[2]；而目前铁路货车评估中尚存在大量的主观数据，基于神经网络模型的重要度评判方法需要在权威且数据成熟的条件下进行，因此也不宜采用。

灰色系统理论是由华中理工大学邓聚龙教授于1982年创立，用来处理信息不完全确知的系统[3]。

针对上述问题，采用层次分析法与灰度关联相结合的方法，计算出货车零部件的权重，就可以实现对铁路货车零部件重要度较为准确的评估。

1 铁路货车零部件评价对象及指标

铁路货车零部件重要度评估要从安全性、任务性、经济性等方面综合考虑其在所属系统运行过程中对系统整体运行产生的影响程度[4]。零部件重要度越高，说明它对所属系统的安全及运营影响越大。

1.1 评价对象

以C80型货车为例，划分了车辆—大部件—零部件的三级层级关系，大部件层级有车体、转向架、基础制动装置、空气制动装置、钩缓装置、轮轴共6个部分，层次结构如图1所示。

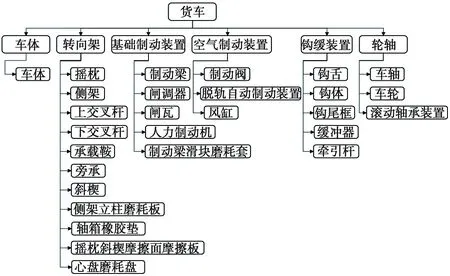
图1 C80型敞车层次分析示意图

零部件的重要度由计算得到的零部件权重来表示，本文中分别对铁路货车6个大部件中的零部件进行了权重计算，得到各零部件在各自对应的大部件中的重要度。

1.2 评价指标

构建适宜于铁路货车的评价指标是零部件重要度评价的基础。理论上，考虑的评价指标越多评判结果越能趋于合理，但过多的评价指标也会增加评判的难度，且各指标的权重系数难以适当分配，因此选用故障易发性和故障危害度两个指标对零部件重要度进行评价[5]。

为了降低主观因素对车辆零部件重要度的影响，结合铁路货车车辆特性和维修保障实际，将故障易发性和故障危害度的等级划分为4级，分别为“常发生故障”“较常发生故障”“偶尔发生故障”“几乎不发生故障”和“严重”“较严重”“中等”“轻度”。具体评级见表1。

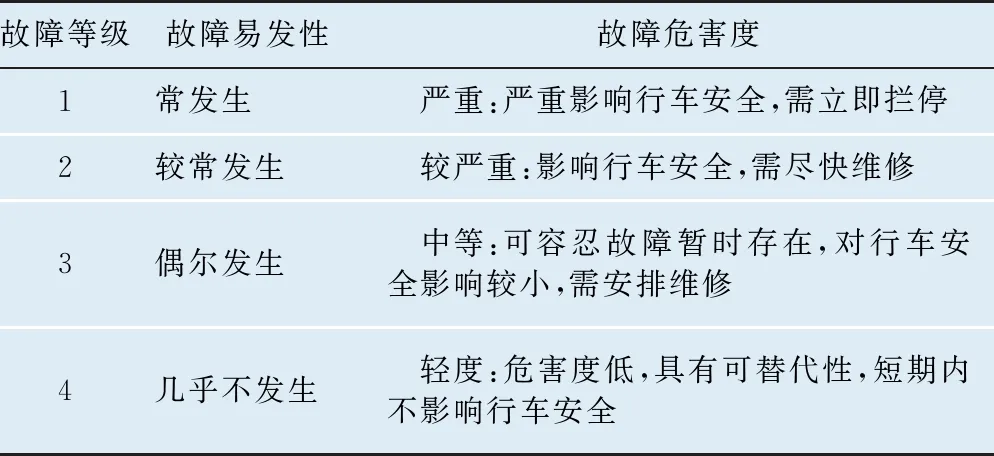
表1 重要度评价指标标准

在计算权重之前，需要通过专家打分的方法对货车零部件进行等级评定，然后进行数据预处理，从而兼顾权重计算时的主观性与客观性，并将定性分析与定量分析相结合。

本文研究过程中，向多位专家进行了问卷调查，专家组成员包括货车车辆维修保障专家、维修技术人员、装备设计人员等，各位专家对零部件重要度进行评分。要求各位专家以匿名方式，根据自己的专业知识和实践经验，独立地给出对各零部件的等级评定结果。

2 铁路货车零部件重要度评价方法

2.1 AHP法确定零部件权值

AHP法确定评价指标权值时步骤如下：

(1) 建立评价目标层次图；

(2) 构建判断矩阵；

(3) 安排一个层次结构来执行判断矩阵的一致性检查；

(4) 计算评价对象权值。

确定各零部件等级后，即可构建判断矩阵，设判断矩阵为C=(Cij)n×n，其重要性标度及其含义如表2所示。

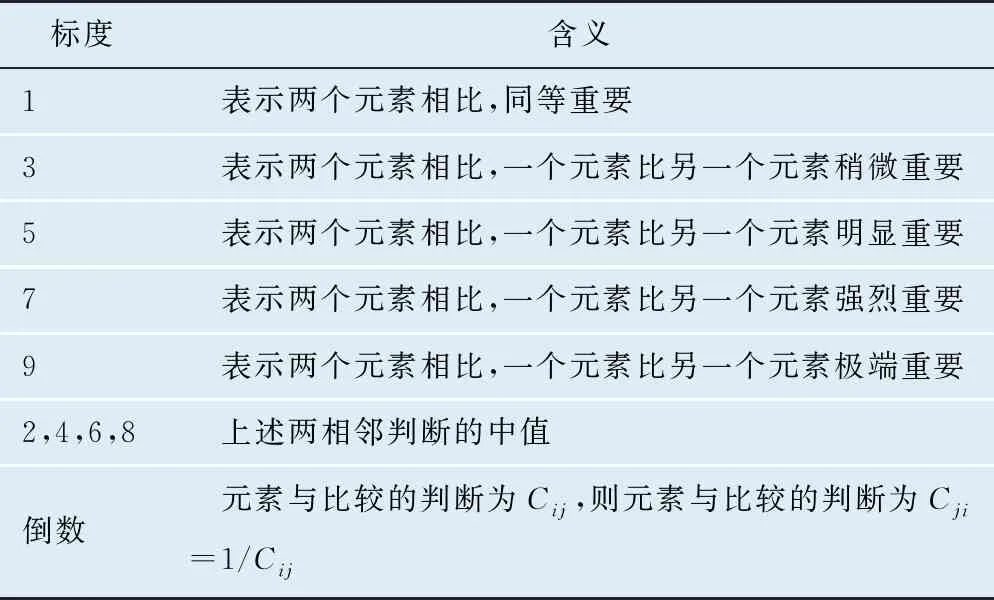
表2 判断矩阵的重要性标度及其含义

根据以上重要性标度划分，把评价指标中的1～4的层级进行分配，评价为1级的标度为9，评价为2级的标度为6，评价为3级的标度为4，评价为4级的标度为1。再采用和积法计算各部件的权重，根据公式(1)进行归一化处理，根据公式(2)计算权重向量。

(1)

(2)

式中：n——判断矩阵的维数；

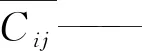
Cij——判断矩阵中的值;

ai——元素的权重值。

然后计算一致性指标CI：

(3)

式中：λmax——判断矩阵的最大特征根。

查找响应的平均随机一致性指标RI(Random Index)，n=1～7的RI值见表3。

表3 平均随机一致性指标RI

计算一致性比例CR：

(4)

当CR<0.10时，认为判断矩阵的一致性可以接受；若CR>0.10，则认为判断偏离一致性过大，需要判断调整矩阵，方法为：使用初始判断矩阵A计算得到其排序权重向量α，再由α构造一个完全一致性矩阵B，然后将A和B进行线性叠加生成矩阵C，计算C的权重向量α*，对矩阵C进行一致性检验，若矩阵C不满足一致性标准，则用矩阵C替换A，重复上述过程，直到得到的矩阵C满足一致性要求为止。

2.2 利用灰色关联度调整评价影响因素

使用灰度相关性可以减少每个专家的主观评价要素，并增加权重计算的可靠性。

以各专家对大部件下具体部位的平均评价打分作为参考值，分析各评价打分对该参考值的关联程度,从而合理分配各个专家评价的权重。具体步骤如下：

(1) 对经过AHP处理后的数据进行归一化。

aij=aij/maxi(aij)

(5)

式中：aij——根据第i个专家的打分结果，对第j个零部件的权重计算情况。

(2) 计算每个目标序列(比较序列)与参考序列的相应元素之间的绝对差值|a0j-aij|，得到绝对差值矩阵，进而计算关联系数。

min|a0j-aij|=0

(6)

max|a0j-aij|=0.5

(7)

(8)

式中：ρ——分辨系数，0<ρ<1。若ρ越小，关联系数间差异越大，区分能力越强，通常ρ取0.5。

(3) 计算各位专家的关联系数及其权重。

(9)

(10)

式中:m——专家总人数；

i——第i位专家；

j——第j个零部件。

(4) 根据专家权重得到最终评估结果R。

R=P×E

(11)

式中：P——通过前面介绍的AHP方法所得到的权值向量；

E——专家的关联系数矩阵。

3 示例分析

以对基础制动装置的零部件重要度进行评定为例，取某专家的打分结果，经数据处理可得到判断矩阵，如表4所示。依据某专家打分结果确定的基础制动装置中有关零部件权值见表5。

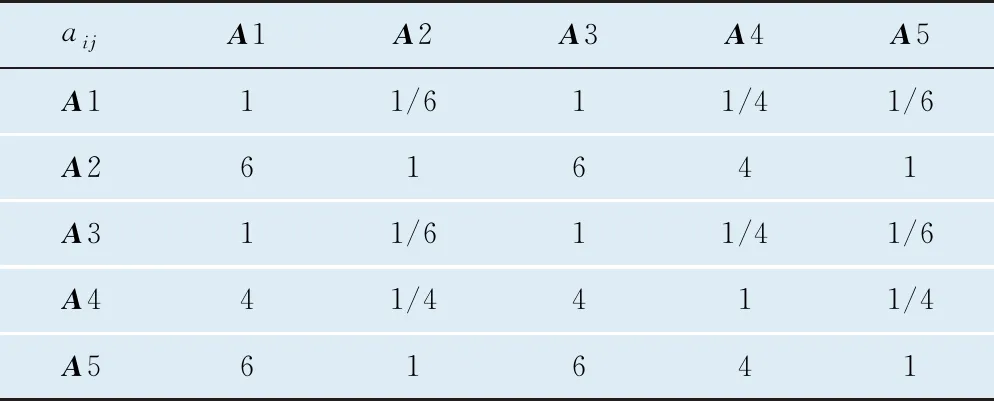
表4 对基础制动装置打分得到的判断矩阵

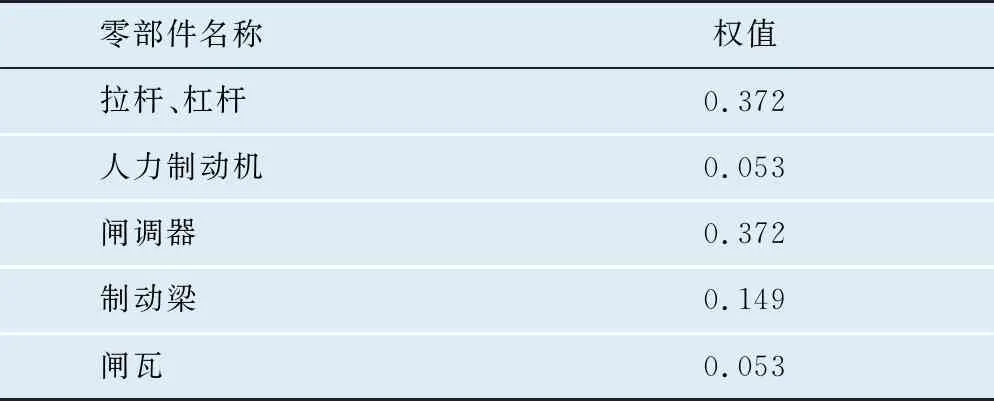
表5 基础制动装置中有关零部件的权值

经层次分析法计算得到每位专家对零部件的评价情况后，综合所有专家的评价情况，利用灰色关联度，合理分配各个专家对最终评价所占的权重。这里以7位专家为例，对数据矩阵进行归一化和绝对差值计算后可得到表6的结果。通过计算关联系数矩阵，可以得到专家关联系数及专家权重，如表7。

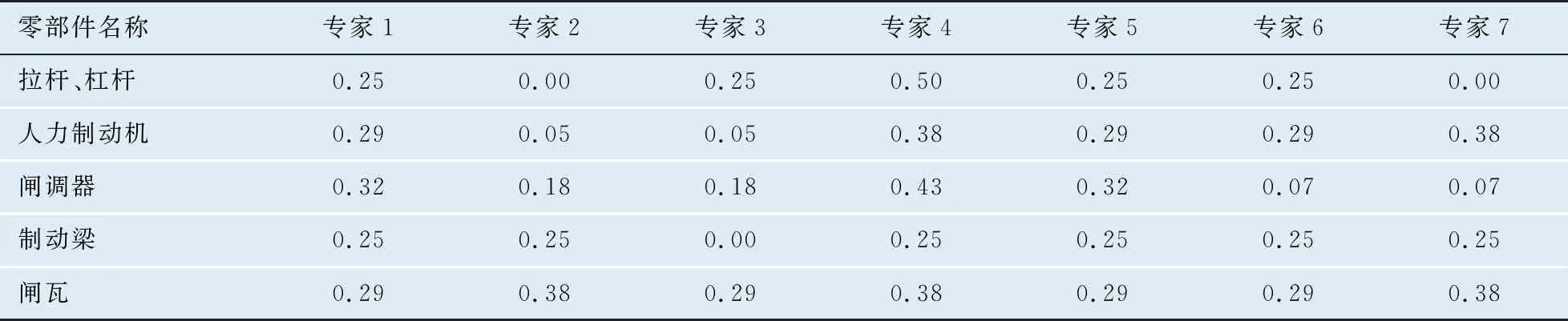
表6 7位专家的评价归一化和绝对差值处理后的结果

表7 专家关联系数及专家权重

最后，基于这7位专家对基础制动装置零部件的打分情况，得到基础制动装置中各零部件的权值，即为各零部件的重要度。

对所有参与货车零部件重要度评定的零部件进行权值计算，可以建立车辆的评价体系，再利用铁路货车实际数据进行计算，可以对零部件重要度评价模型的准确性及合理性进行验证。

4 总结

本文综合利用AHP方法、灰色关联度方法，对C80型货车零部件进行了重要度评价，以基础制动装置为例，得出了基础制动装置中各零部件的权值即重要度，对后续建立铁路货车指标体系、建立列车健康诊断模型以及为铁路货车故障的精准维修提供决策参考。