浮动油封O形圈黏弹性行为研究及结构优化设计*

刘二强 孔令宇 赵广辉 李华英 林金保 贾 有 刘 俊

(1.太原科技大学应用科学学院 山西太原 030024;2.太原科技大学重型机械教育部工程研究中心山西太原 030024;3.山西煤矿机械制造股份有限公司 山西太原 030031)

浮动油封是动密封中机械密封的一种，其由两对浮动油封环和O形圈构成，整体结构主要包括浮动油封座、橡胶O形圈、浮动油封环等。浮动油封在工作状态时，转子高速运转，将介质带入浮动油封环与密封凸肩具有收敛楔形的间隙中，产生的压力使介质形成强力液膜，从而阻止介质从间隙漏出，达到密封的效果。浮动油封在非工作状态时，转子中心与浮动油封环保持一定偏心距，使液体压力与浮动油封环自重和端面摩擦形成平衡力系。由于浮动油封耐磨性好，工作可靠、结构简单等特点，在工程机械中得到了广泛应用[1-3]。

浮动油封尽管结构简单可靠，但由于中工程机械的施役工况恶劣，且多数是重载条件，因此浮动油封常出现异常状况，漏油现象时有发生。许多学者对浮动油封密封性能及机械结构等进行了研究。刘建刚[3]研究了浮动油封间隙与密封结构对密封性能的影响，通过对DO4290型浮动油封腔的受力分析，指出受内外腔锥角和密封胶圈等的影响，浮动油封端面比压要求与浮动油封间隙正确匹配，而间隙匹配过程计算复杂。孙子莹等[4]研究了浮动油封座间隙对其密封性能的影响，指出合理的间隙匹配才能满足密封性能的要求，并设计出了端面比压对浮动油封座间隙变化影响不敏感的结构。孙运友等[5]根据浮动油封结构周向对称性的特征，基于ANSYS 软件建立了浮动油封结构的二维模型，经过对O形圈和浮动油封环之间接触对的分析，研究了不同压缩率下浮动油封断面的作用力，并指出压缩率随载荷增加而线性增加。郝延明等[6]结合浮动油封在履带式支重台车上的应用实践，总结了重载机械浮动油封性能的影响因素。刘俊和任锡义[7]研究了浮动油封O形圈的黏弹性应力松弛行为，指出因应力松弛使密封压力小于密封所需最小压力时，浮动油封将出现漏油现象。LI等[8]研究了航空发动机中浮动油封环在冷/热态条件下的渗漏特征，指出2种密封条件下冷态临界压力比显著大于热态临界压力比。史瑞和吕晓仁[9]用ABAQUS软件建立了浮动油封结构的二维模型，分析不同接触压力和摩擦因数条件下O形圈等效应力的变化，指出摩擦因数对等效应力影响较小，而侧向压力对等效应力影响显著。徐卫鹏[10]基于ANSYS Workbench软件从高分子类材料特性和理论模型入手，对浮动油封进行了有限元仿真并得到了对应的应力应变关系。朱秀梅[11]从刮板输送机链轮轴组浮动油封浮动油封环质量、浮动油封座及轴承座、装配及使用规程等对可能造成浮动密封失效的因素出发，总结生产实践及维护经验，给出了提高链轮组密封可靠性的常见方法。

浮动油封漏油与浮动油封结构、浮动油封座间隙、O形圈磨损、服役环境及O形圈的黏弹性等因素有关。而由橡胶材料制成的O形圈在外力作用下会出现应力松弛或蠕变行为，即安装于浮动油封腔内的O形密封圈在压缩条件下，两组浮动油封环间的压力随时间而变化，进而影响密封带中起密封作用的润滑油膜，表现为浮动油封密封压力降低，甚至可能出现漏油现象。而目前针对由O形圈橡胶材料结构力学松弛引起的浮动油封密封压力降低而导致的漏油现象研究较少，因此为有效防止因橡胶结构松弛及O形圈表面的摩擦损伤引起的浮动油封漏油及失效，本文作者采用实验和有限元分析相结合的方法，研究了浮动油封与时间相关的黏弹性特征，并在此基础上提出一种新的浮动油封结构。

1 浮动油封实验

实验所用浮动油封O形圈结构如图1所示，O形圈橡胶直径为20 mm，周向直径为400 mm。为模拟真实的服役条件，浮动油封由两对浮动油封和O形圈构成，其横截面结构如图2所示。

图1 浮动油封中的O形圈Fig 1 The O-ring in floating oil seal

图2 浮动油封示意Fig 2 Schematic of floating oil sealing structure

实验在室温下在三思CMT05A万能材料试验机上进行。实验分别采用位移和载荷控制模式，将包含O形圈(直径20 mm)浮动油封及工装放入万能试验机平台上开始压缩加载。实验过程中设备自动记录载荷、位移和时间数据。实验首先为以较快位移加载速度进行加载，当位移达到13.5 mm时，保持压缩位移不变2.5 h，完成松弛实验；然后以较快的载荷加载速度进行加载，当载荷达到1 800 N时，保持压缩载荷不变3 h，完成蠕变实验。

2 高聚物黏弹性的力学模型

O形圈作为高分子聚合物材料，具有显著的黏弹性特征。如图3所示，在黏弹性分析中常采用由若干个Maxwell单元串联而成的广义Maxwell力学模型[12]。

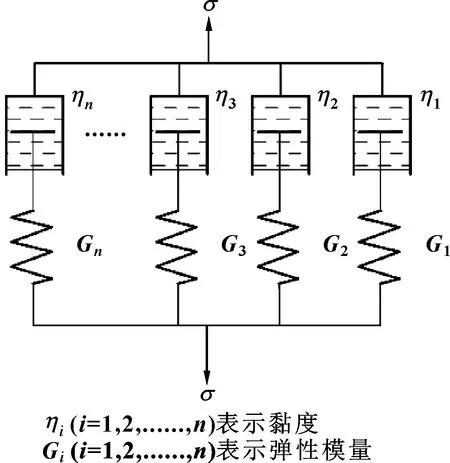
图3 描述橡胶黏弹性行为的力学模型Fig 3 Mechanical model used to describeviscoelastic behavior of polymers

对于应力松弛实验，在保持应变ε0不变的条件下，应力可表达为

(1)

式中：τi为Maxwell单元中黏壶对应的松弛时间。

而对于蠕变实验，在保持应力σ0不变的条件下，应变可表示为

(2)

3 结果与分析

3.1 黏弹性计算与分析

文中选取包含3个Maxwell单元的广义Maxwell模型进行研究，即取i=1,2,3，得出

σ(t)=ε0(G1e-t/τ1+G2e-t/τ2+G3e-t/τ3)

(3)

AΦσ(t)=AΦε0(G1e-t/τ1+G2e-t/τ2+G3e-t/τ3)

(4)

即ΦAσ(t)=AΔΦ(G1e-t/τ1+G2e-t/τ2+G3e-t/τ3)

(5)

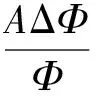
y=B/A(G1e-t/τ1+G2e-t/τ2+G3e-t/τ3)

(6)

即y=C1e-x/t1+C2e-x/t2+C3e-x/t3

(7)

式中：Ci=B/AGi；y为载荷变量；x为时间变量t；ti(t1,t2,t3)对应于松弛时间τi。

如图4所示,利用公式(7)对松弛实验数据进行拟合计算，可得到公式中相应的常数值，见表1。

图4 松弛实验中载荷随时间变化的关系曲线Fig 4 The load-time data and fitting curve for stress relaxation test

表1 载荷时间拟合曲线函数常数的值Table 1 The fitting parameters for stress relaxation test

(2)对于蠕变过程，即保持O形圈所承受压力不变，其压缩量随时间变化的过程，取三单元进行计算，可表达为

(8)

y=A1(1-e-x/t1)+A2(1-e-x/t2)+A3(1-e-x/t3)

(9)

如图5所示，对蠕变实验获得的实验数据进行拟合计算，可得到公式(9)中相应的常数值，见表2。

图5 蠕变实验中压缩位移随时间的变化关系曲线Fig 5 The displacement-time data and fitting curve for creep test

表2 位移时间拟合曲线函数常数的值Table 2 The fitting parameters for creep test

3.2 黏弹性模型建立及有限元分析

橡胶为典型的黏弹性材料，浮动油封O形圈在压缩过程中会发生非线性黏弹性变形。为进一步研究浮动油封O形圈的接触变形问题，准确预测浮动油封因黏弹性变形而导致的漏油失效现象，采用ANSYS软件对浮动油封O形圈进行有限元模拟。考虑对称性，如图6所示，选择浮动油封一侧建立模型，同时考虑浮动油封结构周向对称性，为简化计算模型选用二维模型。

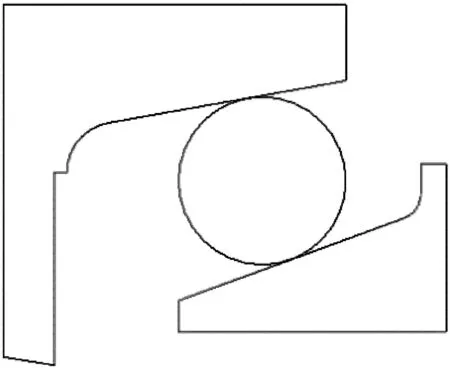
图6 浮动油封的二维模型Fig 6 The two-dimensional model for floating oil sealing structure

橡胶材料可近似为不可压缩体，取泊松比μ=0.5。基于Mooney-Rivlin本构模型[5,13]，橡胶材料的弹性模量E可用下式表示：

(10)

同时橡胶材料的弹性模量E与硬度Hr有关，即

lgE=0.019 8Hr-0.543 2

(11)

常温下浮动油封O形圈邵氏硬度约为60±5，研究指出当邵氏硬度60时[5]，E=4.413 7 MPa，C1=0.700 58，C2=0.035 03 MPa，定义摩擦因数0.65[13]。研究选用ANSYS软件中的PLANE182和PLANE183单元，其中PLANE183作为橡胶单元，而PLANE182为浮动油封环和浮动油封座的单元类型，接触对选用TARGE169单元作为目标单元，选择CONTA单元作为接触单元[5]。浮动油封环与浮动油封座由合金钢制成，其刚度远大于橡胶，因此可认为受力接触过程中浮动油封环和浮动油封座不发生变形，即认为变形全部由O形圈变形引起，恒载荷保载蠕变条件下模拟结果如图7所示。可知，O形圈蠕变变形主要处于靠近浮动油封座的位置，越靠近浮动油封座其变形越大，而靠近浮动油封环位置的橡胶材料几乎不发生变形，这种单侧变形的变形模式，非常不利于O形圈的长期使用。同时，受摩擦影响，靠近浮动油封座的O形圈材料不但变形严重，而且容易磨损，从而造成漏油现象。

图7 模拟得到的O形圈位移云图Fig 7 The deformation nephogram of O-ring

分别进行对应实验条件下的松弛过程和蠕变过程有限元模拟，将模拟结果和实验结果进行对比，如图8所示。可知，实验数据与(实验)理论模型计算和模拟得到的浮动油封载荷和蠕变位移的变化趋势一致。有限元模拟结果略低于(实验)理论模型计算结果，这可能与有限元模型建立过程中摩擦因数定义有关。2种计算方式得到的结果相差较小，因此认为建立的有限元模型可用于预测浮动油封O形圈在松弛和蠕变过程中的载荷和位移变化过程，进而为浮动油封结构设计维护和寿命预测提供参考依据。

图8 浮动油封O形圈松弛和蠕变过程理论计算和模拟结果对比Fig 8 Comparison of theoretical calculation and finite elementsimulation results for O-ring under relaxation and creeptests(a)change of load during relaxation process;(b)change of displacement during creep process

由图8可知，随着时间增加，松弛过程出现密封压力的逐渐减小，而蠕变过程则出现蠕变位移的逐渐增大。因此对应于浮动油封的实际工况，如若浮动油封受载形式为恒定位移，则可能出现密封压力逐渐降低，当密封压力低于密封压力阈值时，浮动油封则会因O形圈的松弛而出现漏油现象；如若浮动油封受载形式为恒定载荷，则会出现浮动油封O形圈的压缩位移随时间而逐渐增大的现象，当O形圈压缩位移超过一定阈值后，则出现恒载荷值降低，即由于浮动油封O形圈蠕变会引起密封压力降低，导致油液渗漏。

3.3 一种新的浮动油封结构

鉴于浮动油封由于结构松弛和O形圈与浮动油封座引的摩擦损伤可能引起浮动油封的漏油现象，研究人员针对性地提出一些浮动油封的创新设计。WANG[14]提出了一种包括安装底座、密封圈底座和密封圈，具有耐磨性能和吸收补偿功能的浮动油封结构。文献[15]发明了可在多种工况下使用的WD200/500系列浮动油封，其采用多腔体设计理念，将密封功能分段和分级处理，便于维修维护。本文作者所在的研究团队根据上述分析结果，也提出了一种新的浮动油封结构设计构想，具体如图9所示[16]。为减小O形圈与浮动油封座引的摩擦损伤，在浮动油封环及浮动油封座与O形圈之间分别垫衬内外聚四氟乙烯(PTFE)衬圈；考虑O形圈橡胶的应力松弛特性，在外PTFE衬圈与浮动油封座加装若干个压力补偿恒压弹簧，进而综合解决了由O形圈摩擦损伤和橡胶应力松弛引起的漏油现象。如图8(a)和8(b)所示，未加装压力补偿弹簧时，在松弛条件下随承载时间增加O形圈的密封压力逐渐减小，在蠕变条件下O形圈的蠕变压缩位移逐渐增大。而在结构中安装压力补偿弹簧后，松弛条件下弹性力可补偿由于O形圈应力松弛造成的密封压力减小，而又由于该弹簧为恒压弹簧，故可保证了密封压力不会随时间而改变；而蠕变条件下，恒压补偿弹簧为保证接触力的恒定，则需要舒张一定的量，补偿O形圈的蠕变压缩位移，进而保证浮封座与环的间隙不变。

图9 一种包含PTFE垫圈和恒压弹簧的浮动油封新结构Fig 9 A new floating oil sealing structure with PTFEgaskets and constant force springs

4 结论

(1)根据浮动油封结构的周向对称性，基于Mooney-Rivlin本构模型，建立浮动油封O形圈黏弹性模型，采用ANSYS有限元软件对浮动油封结构的松弛和蠕变过程进行了有限元分析，结果表明，该模型可用以预测浮动油封O形圈在松弛和蠕变过程中的载荷或位移变化过程，进而为浮动油封结构设计维护和寿命预测提供参考依据。

(2)通过实验和力学模型的理论计算，研究了浮动油封结构中O形密封圈的黏弹性行为。结果表明：松弛过程中密封压力随时间增加而逐渐减小，蠕变过程则出现蠕变位移逐渐增大的现象。

(3)O形圈应力松弛和蠕变均可能导致浮动油封的漏油失效，同时考虑O形圈与浮动油封座的摩擦损伤可能引起的浮动油封漏油现象，提出了一种包含PTFE垫圈和恒压弹簧的浮动油封新结构。