串列叶片气动设计及优化
2021-08-27刘宝杰于贤君安广丰周安宇李丽丽
刘宝杰,于贤君,安广丰,陶 源,周安宇,李丽丽
(1.北京航空航天大学航空发动机研究院,北京100191;2.航空发动机气动热力国防科技重点实验室,北京100191;3.中国民航大学航空工程学院,天津300300;4.中国航发沈阳发动机研究所,沈阳110015)
0 引言
进入喷气时代以来,航空发动机的推重比已经从最初2~3提高到10左右,下一代军用航空发动机的推重比期望突破12;此外,为了满足未来高超声速飞行的需求,航空发动机压缩系统的工作温度会大幅度升高,控制压缩系统的长度,减轻压缩系统的质量,对于涡轮基动力装置具有重要价值。这些都要求未来航空发动机压气机的平均级负荷系数要达到0.45~0.50,远高于目前常规叶片压气机的负荷极限(对应的负荷系数约为0.40),因此必须探索和突破更高负荷水平的压气机设计技术。串列叶片作为一种先进叶片气动布局形式,不仅能够实现更高的气动负荷水平,而且具有较好的工程可行性,已成为当前探索的下一代航空发动机先进设计技术的热点之一。
国内外针对串列叶片设计技术的研究主要集中在3方面:(1)串列叶片相对于常规叶片的性能优势。在这方面,虽然在美国航空航天局的支持下,PW公司开展了大量的级环境下的试验研究[1-3],但由于所设计的压气机负荷偏低,并未显示出串列叶片具有明显的性能优势;级环境下的流动较为复杂,Hoeger等[4]、Schneider等[5]、Dehkharqani等[6]、苗厚武等[7]尝试从更为简单的2维叶栅对比中展开研究,但相对常规叶片,在不同情况下串列叶片的损失水平有高有低,并未从更简单层面理清这一问题。(2)串列叶片流动机理。在这方面,国内外开展的研究最多,得到的结论也较为统一,其中后排叶片新发展的附面层、前后排叶片之间重叠区域形成的缝隙流动、后排叶片前缘对前排叶片的势作用等,是调控串列叶片流动损失从而使其发挥出性能优势的主要贡献点。(3)串列叶片前后排叶片相对位置及参数分配。在这方面,包括对基于势流理论的分析[8-10]、数值仿真[11-13]与试验研究[7,14-15]以及结合CFD技术的数学寻优[16-18]等研究表明,当串列前后排叶片轴向相对位置在近似为零的轴向重叠附近、周向相对位置在后排叶片靠近前排叶片压力面附近、前后排叶片负荷分配比选为1附近,可以获得更小的总压损失和更大的失速裕度。
综上所述可知:(1)串列叶片相对于常规叶片的性能优势及优势区间尚不明确;(2)针对亚声速串列叶片的研究已经逐渐成熟,但考虑前后排叶片相互影响的气动设计方法并不完善;(3)针对超/跨声速串列叶片的研究相对较少,考虑复杂激波系影响下最优的流动组织形式远未形成统一认识,前后排叶片匹配工作规律尚待深入研究归纳。针对上述问题,本文分别从串列叶片基本理论及流动机理、串列叶型的优化设计、串列叶片在亚/跨声速压气机设计中的应用3方面进行研究,以期促进对于串列叶片设计技术的认识,为中国突破更高负荷水平的压气机设计技术提供相关理论支撑。
1 串列叶片扩压极限
为了探索串列叶片的扩压极限及其相对于常规叶片的性能优势及优势区间,完善了Koch[19]在1981年给出的探索常规叶片扩压极限的方法,在此基础上发展了串列叶片扩压极限模型,并在单级低速大尺寸压气机试验台上对该模型进行了试验验证。
1.1 常规叶片扩压极限模型
对于1个典型2维扩压器,当其扩压长度N与进口宽度W1的比值固定时,随扩压器的扩张比W2/W1的增大,静压升系数Cp表示的扩压器气动负荷表现出先增大后减小的趋势,扩压器静压升系数特性如图1所示。对于不可压流动而言,根据伯努利方程和连续方程可推导得到上述2维扩压器的静压升系数与扩压器进出口宽度之比以及扩压器内部总压损失系数的关系式
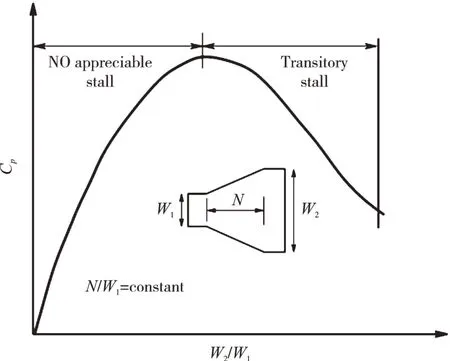
图1 扩压器静压升系数特性
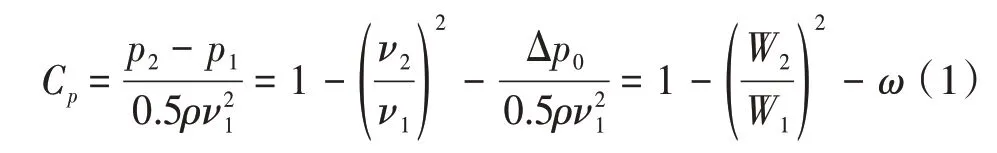
式中:p1、p2分别为扩压器进出口的静压;v1、v2分别为扩压器进出口的速度;Δp0为扩压器进出口的静压之差;ω为流体经过扩压器的总压损失系数。
基于Aungier[20]给出的2维扩压器特性关联,可以得到扩压器达到最大静压升系数(Cp,max,用于表征扩压极限,下同)时,扩张比W2/W1与用进口宽度无量纲化的扩压长度的关联关系,再通过一系列的简单代数计算可得达到最大静压升系数Cp,max时扩张比W2/W1与用出口宽度无量纲化的扩压长度的关联关系
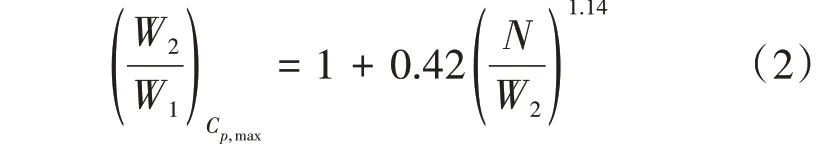
常规叶片S1流面如图2所示。图中,g1和g2分别为2维叶型进出口流道宽度,L为具有与2维叶型相同弦长、相同弯角的等效圆弧型中弧线的长度,对于1个压气机2维叶型,上述扩压器的进出口宽度W1和W2可由图2中g1和g2代替,扩压长度N可由图2中L代替。其中g2和L又可分别表达为2维叶型的常用几何参数的关系式

图2 常规叶片S1流面
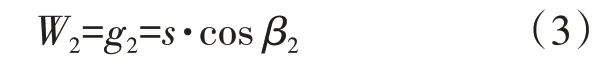
式中:β2为叶型出口气流角。
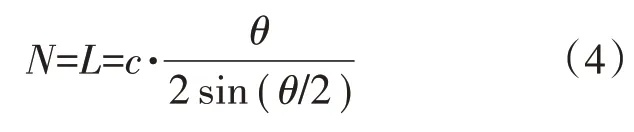
式中:c为叶型弦长;θ为叶型弯角。
因此,式(2)中的N/W2可表达为叶型的常用几何参数的关系式
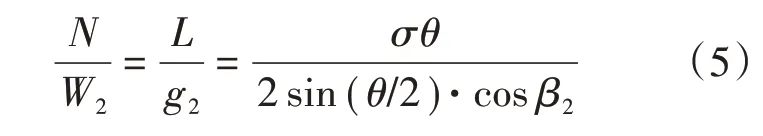
式中:σ为叶型稠度。
根据式(1),当模化得到最大静压升对应的扩张比W2/W1之后,还需要得到2维叶型的总压损失ω才可以获得最大静压升系数Cp,max。其实,叶片损失的产生本质上与叶片表面附面层的发展紧密相关,将叶片总压损失与叶片表面的附面层参数相联系是合理的模化方法。Wennerstrom[21]给出了动量厚度与损失的关联式中:δ*为附面层动量厚度;f(DF)为以D因子作为独立变量的单变量函数,D因子为扩散因子。
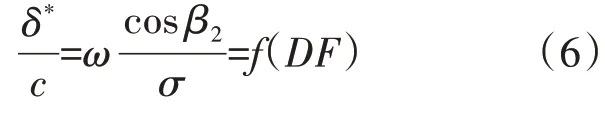
出于简化的目的,将式(5)代入式(6)得到以L/g2为变量的简化损失关联式
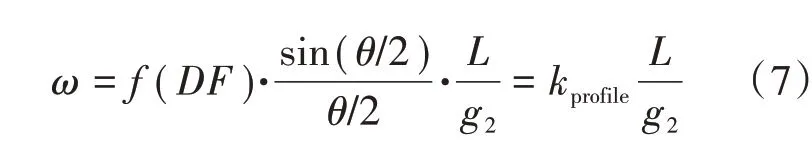
式中:kprofile为经验系数。
作为一种简单评估方法,当叶型选定后可以用经验系数kprofile近似评估近失速点的损失水平,对于本文研究的CDA低速叶型而言,kprofile=0.06。
将式(2)、(7)代入式(1)得到2维叶型最大静压升系数与以L/g2为自变量的单变量函数的关系,从而将1个2维叶型的扩压极限与2维叶型的几何与气动参数有效关联(图2)。从图2中可见,当L/g2<2.5时,最大静压升系数Cp,max随L/g2的增大呈现快速增大的趋势;当进一步增大L/g2时,2维叶型最大静压升系数会遇到1个极限值约为0.66,显然该值就是本模型给出的所有常规叶片压气机2维叶型所能达到的扩压极限。
1.2 串列叶片扩压极限模型
对于串列叶片而言,同样可以根据上述方法对前后排叶片的扩压极限分别进行模化,然后再利用式(8)来表征串列叶片整排的扩压极限
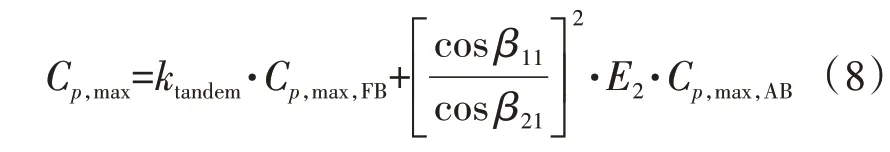
式中:Cp,max,FB、Cp,max,AB分别为前、后排叶片在单独工作条件下的最大静压升系数;ktandem和E2分别为串列叶片近失速状态时前、后排叶片静压升系数与各排叶片单独工作的最大静压升系数的比值。
由于串列叶片随工况变化时后排叶片攻角几乎不变,所以当串列叶片整体达到最大静压升时,可认为前排叶片也达到最大静压升。但考虑到前后排叶片相互作用时前排叶片的静压升系数与前排单独工作的差别,ktandem可能不完全等于1。4种不同D因子情况下前排叶片在串列与单独工作条件下最大静压升系数及其比值如图3所示。从图中可见,前排叶片在串列与单独工作条件下,最大静压升系数的比值几乎不随D因子增大而发生变化。因此可以取ktandem=1.1,用于本文对串列条件下前排叶片最大静压升系数的计算。

图3 前排叶片最大静压升系数
对于后排叶片而言,由于其攻角几乎不随工况发生变化,所以其静压升系数也几乎保持恒定。但为保证后排叶片工作在合理的气动条件下,设计时需要选取合理的攻角状态使其略微远离失速边界而又能发挥最大扩压作用。1组保持前排叶片几何形状和后排叶片出口几何角不变,通过改变后排叶片弯角得到的串列叶片静压升系数及总压损失随E2的变化曲线如图4所示。从图中可见,存在最佳的E2使得损失最低、静压升最高。由此确定E2的最佳值。
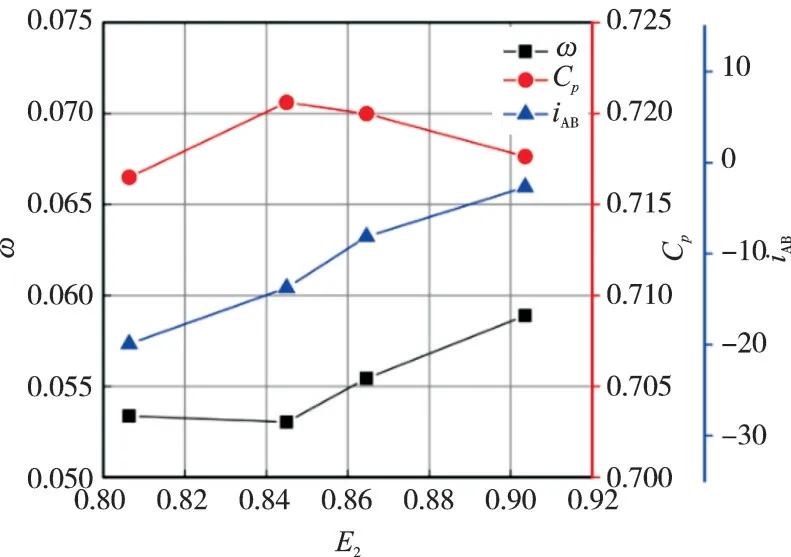
图4 在不同E2近失速工况下串列2维叶型的损失静压升性能及后排叶片攻角
1.3 串列与单排工作条件下的扩压极限对比
为了对扩压极限模型进行校验,首先利用一些有限的试验结果对常规2维叶型的扩压极限模型进行校验,结果如图5所示。从图中可见,这些叶片最大静压升系数的试验值几乎都高于Koch模型的预测值而低于本文模型的预测值,从而验证了本文所发展的适用于常规叶片的扩压极限模型。

图5 常规2维叶型扩压极限模型
对于串列2维叶型的数值模拟结果与扩压极限模型的对比如图6所示。从图中可见,模型预测得到的最大静压升系数Cp,max随L/g2的变化更加显著,但Cp,max随L/g2的变化趋势可以被串列叶片扩压极限模型所捕捉;此外,常规叶片的最大静压升系数约为0.66,而串列叶片的可以提升到0.74甚至更高。因此,当实际的超高负荷压气机设计的最大静压升系数趋近于0.66时,串列叶片将是更优的选择,可保证足够的裕度。
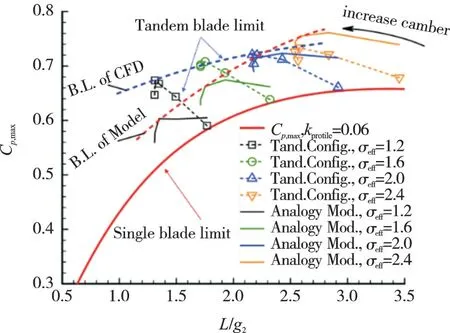
图6 串列2维叶型扩压极限模型
1.4 扩压极限模型的试验验证
为了对常规和串列叶片的扩压极限模型进行验证,设计了基于叶尖负荷系数为0.46的常规叶片单级压气机[22],为了与常规叶片进行对比,基于相同的设计方法并选用几乎相同的关键设计参数,同时设计了基于叶尖负荷系数同为0.46的串列叶片单级压气机,并对二者进行了详细的试验研究。
为了选取较为合适的典型设计参数,利用重复级速度三角形分析模型,针对典型设计参数对压气机效率和裕度的影响规律进行评估。最终选取的设计点流量系数为0.55,反力度为0.7,转、静子稠度分别为1.90和2.15。此外,为了使常规高负荷叶片和串列叶片具有可比性,在串列叶片的设计中,维持1维参数与常规叶片的相同,同时保持不同叶高的速度三角形一致。对于串列叶型的研究,其特有的设计参数如轴向相对位置LAO、周向相对位置Lpp、负荷分配和稠度比等,都选取在使串列叶片工作效率较高的范围内。经过CFD优化后最终的串列及常规叶片压气机几何造型如图7所示,二者主要设计参数的对比见表1。
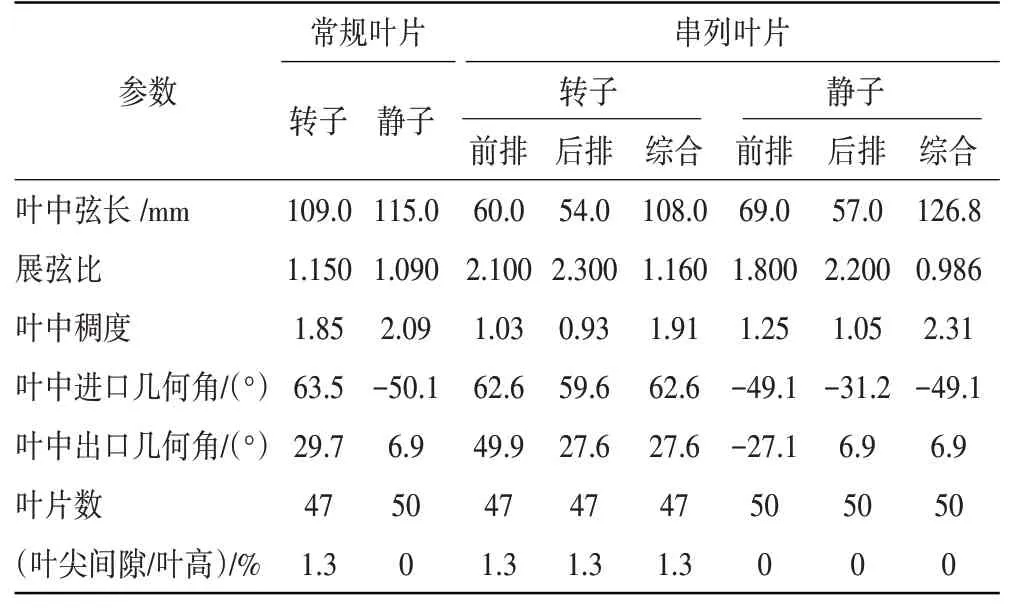
表1 常规及串列叶片压气机主要设计参数
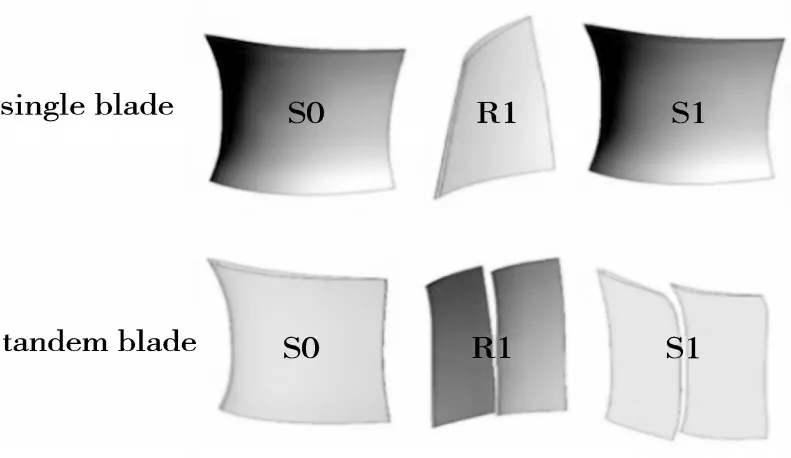
图7 常规及串列叶片压气机几何造型
2套压气机测量得到的特性对比如图8所示。从图中可见,试验测量的串列叶片在设计点的负荷系数达到了设计目标,而常规叶片则略小于目标值。此外,相比于常规叶片,串列叶片的设计点效率从91.4%提升至92.0%,最高效率提升了约1%,综合裕度从16.9%拓宽至22.3%。在相同负荷系数下的效率对比如图9所示。在较小的负荷系数下工作时,常规叶片效率高于串列叶片的;当负荷系数为0.415~0.460时,串列叶片和常规叶片的效率相当;当负荷系数大于0.46时,串列叶片表现出明显的优势。因而可以将负荷系数0.46作为串列叶片优势区间的临界点。同时串列叶片的极限负荷系数可达到0.52,如果以最高效率点为基础,串列叶片的负荷裕度比常规叶片的高约8.3%。
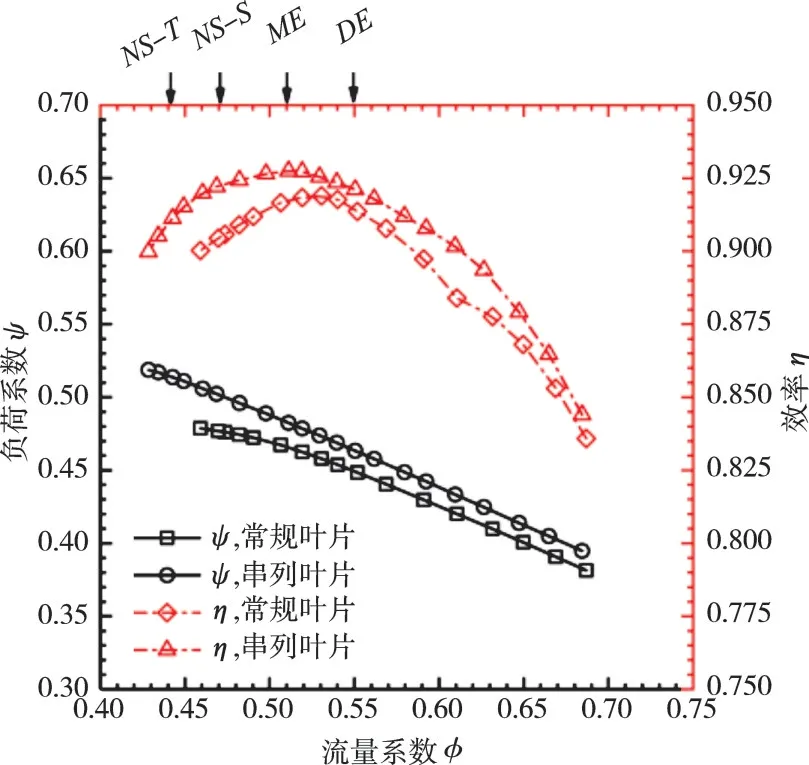
图8 常规叶片和串列叶片负荷和效率特性对比
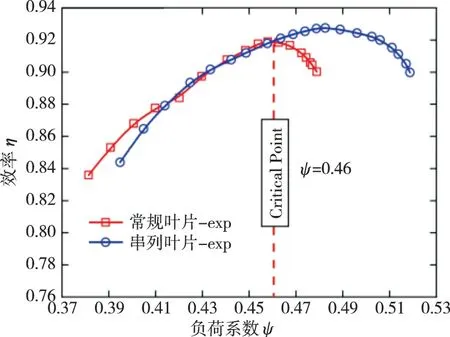
图9 常规叶片和串列叶片在相同负荷下的效率对比
为了进一步说明串列叶片拓宽压气机扩压极限的能力,对试验测量的常规叶片和串列叶片在典型流量系数下的静压升系数进行了对比,结果如图10所示。从图中可见,串列转、静子的最大静压升系数比常规转、静子的分别高8.3%、10.2%。串列转子与常规转子静压升系数与其最大静压升系数的对比如图11所示。从图中可见,对于常规叶片而言,其设计点静压升系数与近失速点静压升系数的比值(即图中E值)为0.92,而串列叶片的E值为0.86,即串列转子相对于常规转子具有更大的静压升裕度。此外,串列转子近失速点的静压升系数已经超出了常规2维叶型的扩压极限,可以更为直观地显示出串列叶片的极限扩压优势。
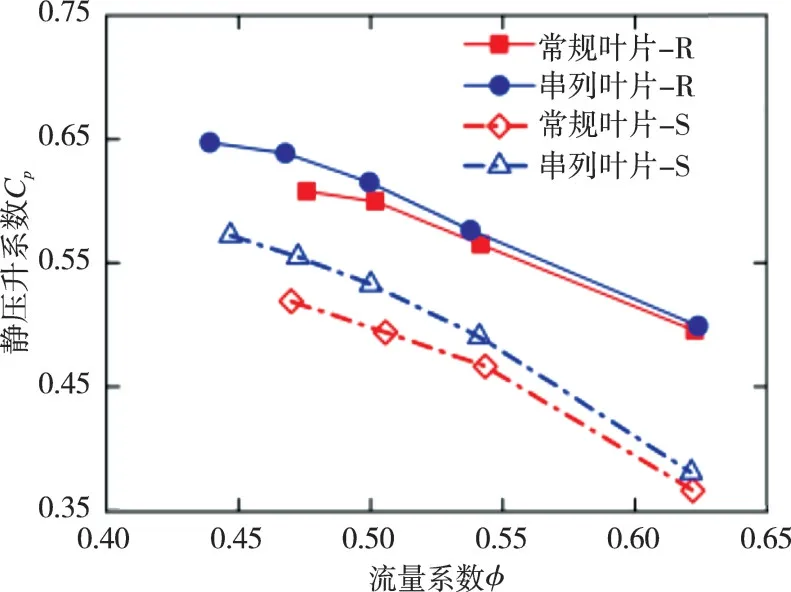
图10 常规叶片和串列叶片在典型流量系数下的静压升系数

图11 常规转子和串列转子的静压升系数与扩压极限对比
2 串列叶型设计技术的发展与应用
基于模型的理论分析证明了串列叶片的性能潜力,揭示了前后排叶片的匹配工作规律,初步探明了串列叶片能够发挥负荷优势的区间。为了将串列叶片应用于工程实际,从流动机理和设计方法入手,在保证串列叶片负荷水平的前提下,以降低流动损失、拓展叶型工作范围为目标,开展了串列叶型的设计技术研究,揭示了前后排的相互影响机制,发展了基于中弧线修型的快速优化设计方法并融入传统造型体系。研究分为亚声速和超声速流动2部分。
2.1 亚声速串列叶型设计技术
当前国内外针对亚声速串列叶型设计技术的研究较丰富,也基本确定了前后排叶片相对位置、弦长、负荷分配等设计参数的最优区间。但传统压气机设计体系在设计过程中无法考虑串列叶片前后排的气动耦合,限制了叶型性能的进一步提升。为此,本文以当前公认的串列叶型参数最优区间为基础,在来流马赫数为0.8的条件下,完成了亚声速串列叶型的设计技术研究:(1)通过前后排单独工作与串列条件下流动特性的对比,揭示了串列叶型前后排的相互影响机制;(2)以串列叶型最优相对位置、稠度、负荷分配为基础,发展了一种基于“中弧线修型”的串列叶型快速优化设计方法,验证了设计思想的合理性。
2.1.1 串列条件下前排叶片工作特性分析
为了理清串列条件下后排叶片对前排的影响机制,在来流马赫数为0.8、攻角状态相同的条件下,对比了前排单独工作和串列条件下的流动特性。研究发现,在串列条件下前排叶片的损失比单独工作时的增加了约8%,如图12所示。前排叶片损失发生变化的主要原因是串列条件下前后排叶片相互影响。进一步对比了典型攻角状态下前排单独工作和串列条件下的叶表等熵马赫数分布,如图13所示。前排单排的马赫数分布非常接近可控扩散叶型的理想流动状态;但在串列条件下,由于后排叶片的滞止作用在前排尾缘附近叠加了1个额外的压力场(图9),前排压力面气流速度降低,尾缘附近的负荷增大,即后排叶片的势作用降低了前排压力面附近的气流速度,这是导致前排叶片偏离可控扩散叶型分布和损失增加的根本原因。当来流马赫数为0.8、来流攻角为-1°时,前排叶片单独工作和串列条件下流场静压分布对比,如图14所示。
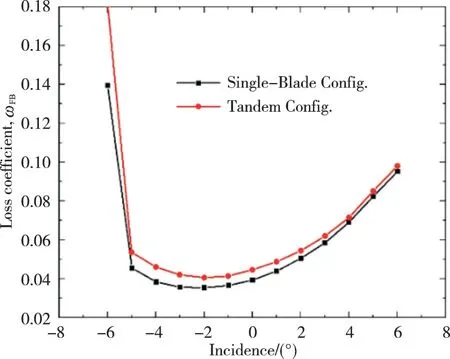
图12 当来流马赫数为0.8时,前排叶片单独工作和串列条件下的攻角-损失特性对比
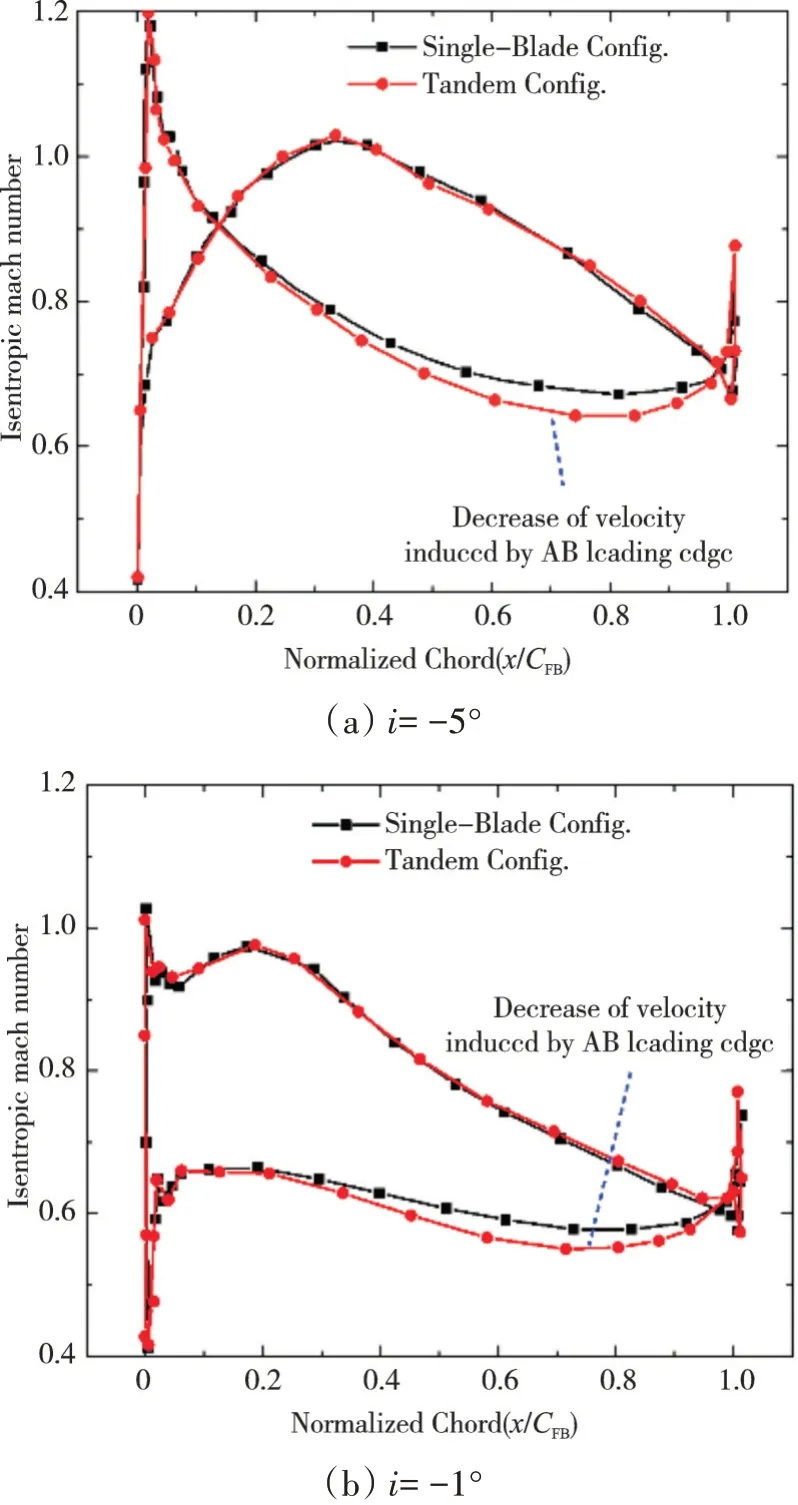
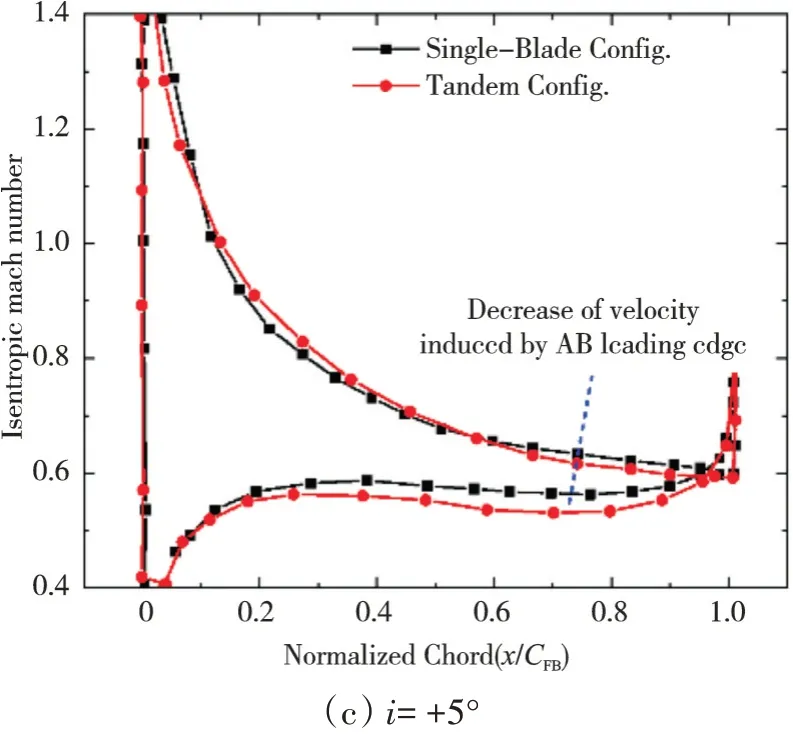
图13 当来流马赫数为0.8时,在不同来流攻角下前排叶片单独工作和串列条件下的叶表等熵马赫数对比
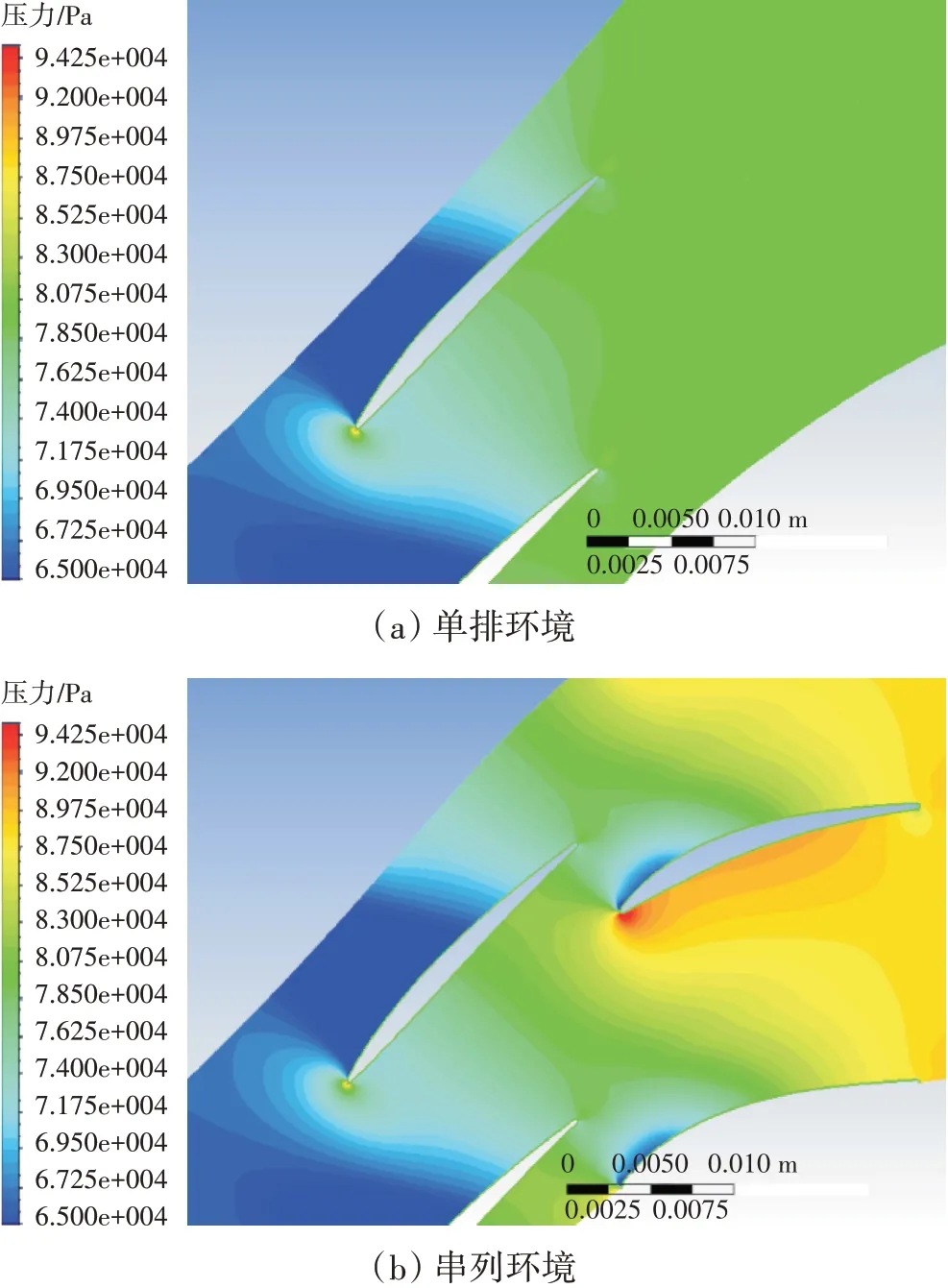
图14 当来流马赫数为0.8、来流攻角为-1°时,前排叶片单独工作和串列条件下流场静压分布对比
2.1.2 串列条件下后排叶片工作特性分析
模拟后排叶片的单独工作需要在串列条件下从前后排叶片的轴向间隙中提取后排叶片进口马赫数和气流角,以此作为进口边界条件。在不同来流攻角下,后排叶片单独工作和串列条件下的叶表等熵马赫数对比如图15所示。串列条件下后排流动特性有2点重要变化:(1)在负攻角和零攻角条件下,缝隙射流的加速作用使后排前缘吸力面附近形成低压区,并使后排前缘局部更容易形成正攻角的速度分布;(2)在较大的正攻角条件下,前排尾迹严重堵塞了后排通道(如图16所示),显著改变了后排叶片的扩压过程,后排叶片表面等熵马赫数整体提高了0.1;另一方面,前排尾迹的堆积压缩了后排主流区的有效流通面积,在一定程度上减小了后排近尾缘处的气动负荷,抑制了后排吸力面的分离。
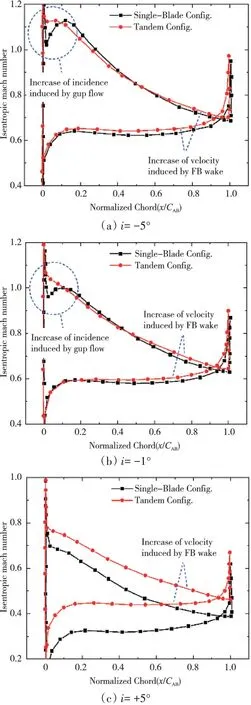
图15 前排叶片表面等熵马赫数分布在单排及串列条件下的对比
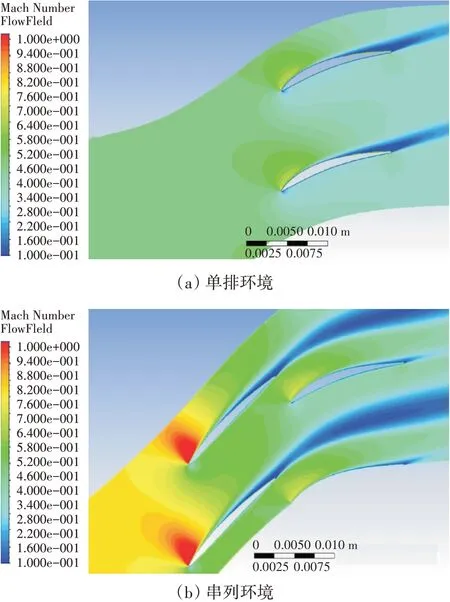
图16 当来流马赫数为0.8、前排来流攻角为+5°时,后排叶片单独工作和串列条件下的流场对比
2.1.3 亚声速串列叶型优化设计
对亚声速串列叶型流动机理进行分析,发现以势作用、缝隙射流为主导的无黏流动特征是前后排相互影响的主要物理机制。尽管气动耦合较弱,但仍然会引起潜在的损失,并且在常规设计体系中无法考虑这一影响,是叶型优化设计中需要重点关注的问题,即轴向/周向相对位置、稠度、弯角分配等参数都选定在已有认识的最佳区间内,如何在保持叶型负荷的条件下进一步降低流动损失,拓展可用攻角范围。为此,本文发展了一种中弧线快速修型方法,通过前/后排中弧线、后排名义攻角等变量控制串列叶型前后排的相互干涉,以适应串列叶型势作用、缝隙射流的影响。
优化前后叶型几何对比如图17所示。在来流马赫数为0.8的条件下,优化前后的串列叶型攻角-损失特性和攻角-D因子特性对比如图18所示。从图中可见,在保证串列叶型负荷水平相同的条件下,设计点损失减少了6%,且负攻角范围拓宽了约2°,优化方案的可用攻角范围接近12°。
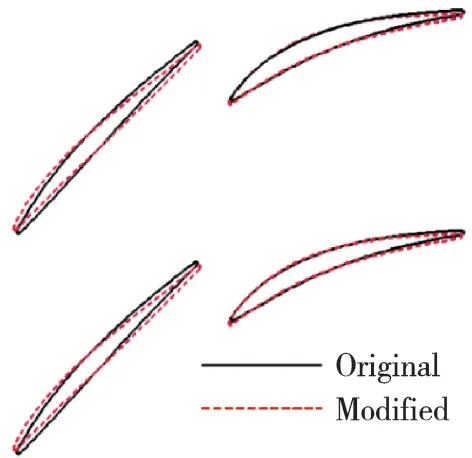
图17 优化前后叶型几何对比
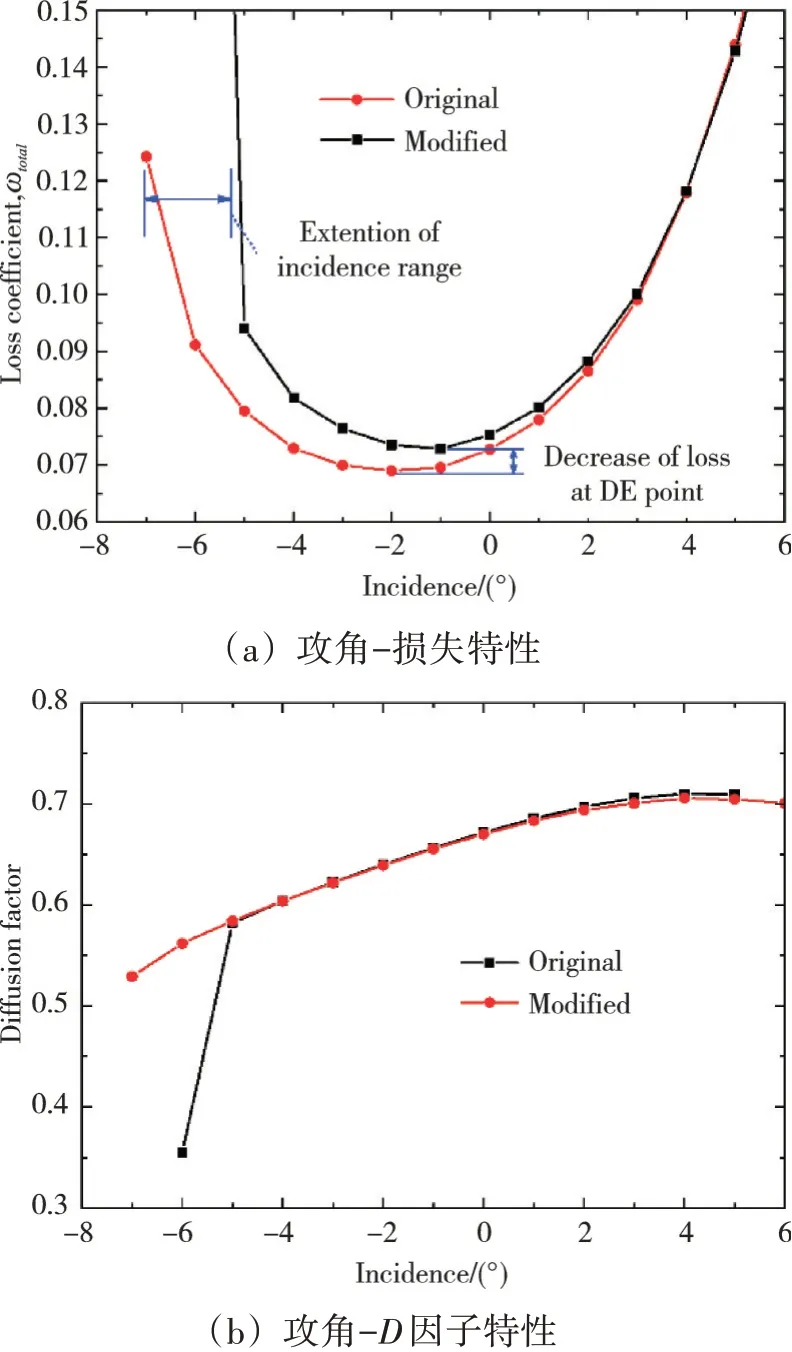
图18 优化前后叶型的攻角-损失特性及攻角-D因子特性对比
优化前后叶片表面等熵马赫数分布的对比如图19所示。调整后前排叶片的气动负荷前移,压力面等熵马赫数基本保持不变,马赫数整体分布更接近可控扩散叶型理想的分布形式;在全工况范围内,后排局部攻角状态发生了明显改变,优化方案更加接近零攻角状态,这对于全工况范围内减少后排叶型损失都是有利的。总之,优化方案在保持前后排相对位置、弯角、稠度分配不变的条件下,基于中弧线的修正进一步提升了叶型性能。对大量的数值验算进行分析结果表明,对于气动耦合较弱的亚声速串列叶型,维持前后排近似可控扩散叶型的等熵马赫数分布较为理想的流动组织形式。
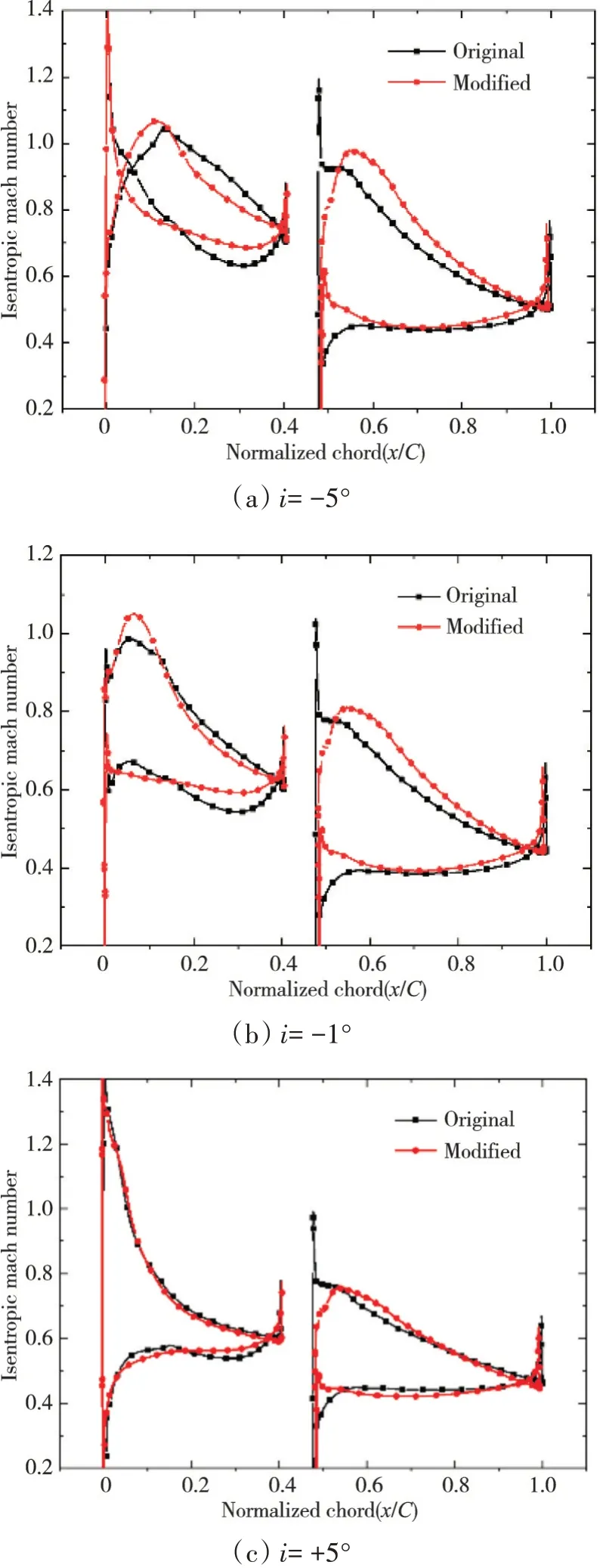
图19 优化前后叶片表面等熵马赫数分布对比
2.2 超声速串列叶片设计
超声速串列叶型的典型特点是由于耦合了复杂激波系的作用,导致相互影响程度明显强于亚声速叶型的,且叶型性能对叶片几何参数的变化更加敏感,因此设计难度更大,目前国内外尚未形成统一认识。为此,针对超声速串列叶型开展了流动机理分析及参数化造型研究,以明确激波影响前后排匹配工作的物理机制,并在典型几何参数约束条件下开展叶型优化设计,在保证基元负荷水平的条件下,有效控制叶型的流动损失。
2.2.1 周向/轴向相对位置的选取
在典型前后排叶片不同轴向相对位置LAO下,研究了串列转子前后排叶片周向相对位置LPP对其气动性能的影响(LAO、LPP的定义参考文献[23]),只对LAO为0.1时的情况展开详细的讨论,其它LAO下的分析方法与之类似。
在反压相同、LPP不同时串列转子叶尖截面的激波结构对比如图20所示。从图中可见,随着LPP的不断减小,前叶片的工作状态慢慢地远离堵点,激波系也逐渐地由双波结构向单波结构蜕化。此外,串列转子流场的另1个显著特点是前排叶片的尾迹在后排叶片中流动。尾迹在后排叶片中不断地耗散,并与主流发生掺混,减小了有效流通面积,造成明显的堵塞。而LPP对该尾迹区也有较大的影响。当LPP减小到0.4时,叶尖截面的尾迹显著增强,因此所造成的堵塞和损失也更大。

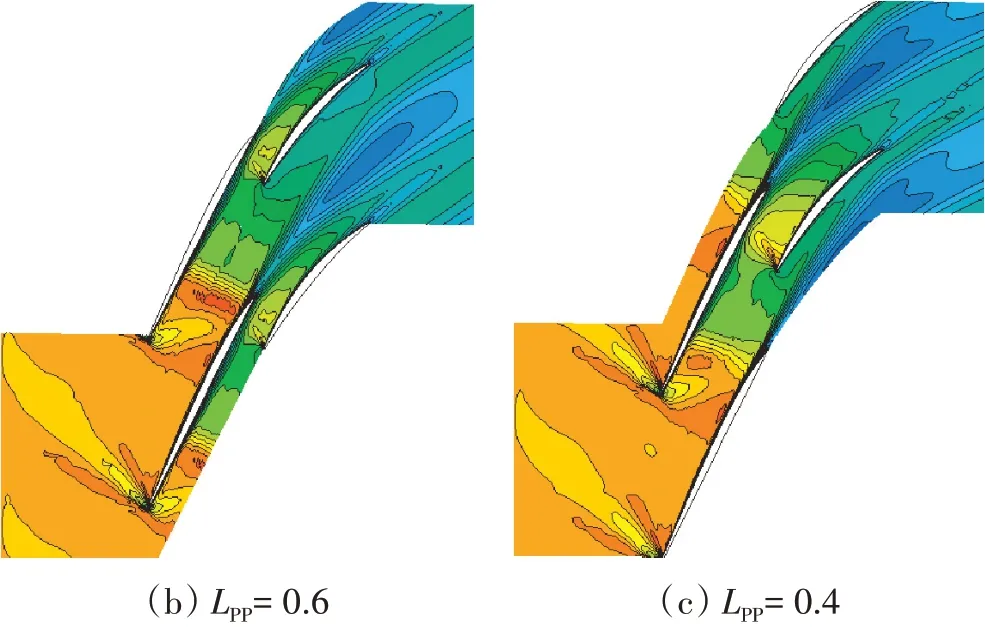
图20 在不同LPP下串列转子叶尖截面的马赫数分布对比
与周向相对位置相类似,串列转子前后排叶片轴向相对位置LAO的变化对激波结构、气动性能也有重要影响,因此在不同的LPP下,分析了LAO对转子叶尖激波结构的影响规律,并总结了最佳LAO的选取区间。
在反压相同、LPP分别为0.8、0.4时,叶尖激波结构随LAO的变化对比如图21所示。从图中可见,LAO对转子叶尖激波结构有较大影响,即存在1个合适的LAO,使得前排叶片叶尖的双波结构最为明显,但不同的LPP所对应的最佳LAO并不相同;当LAO小于最佳值并减小时,前排叶片的叶尖激波结构迅速由双波向单波结构蜕化,串列转子的特性也随之恶化。此外,前排尾迹在后排叶片中不断地扩散,随LAO的增大,尾迹掺混得越均匀,较小的LAO尾迹区中包含的低速流体更多。

图21 在反压相同、LPP不同时串列转子叶尖激波结构随LAO的变化
从图21中还可见,串列转子处于最佳LAO时,前后排叶片在流向方向上的相对位置基本相同。这是因为压力扰动是沿流向方向进行传播的,所以激波结构对前后排叶片在流向方向上相对位置的变化最为敏感。因此,以弦线方向为基准,建立了ξ-η弦向坐标系,对前后排叶片的相对位置进行重新分析,以确定最佳的相对位置。实际上,前后排叶片的相对位置在ξ-η和x-r坐标系下存在关联
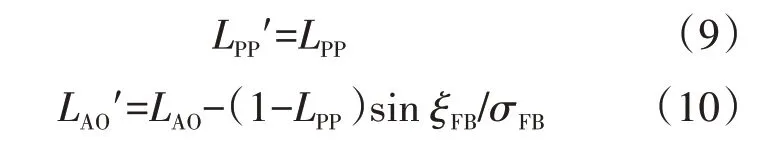
串列转子的失速压比和峰值效率在ξ-η坐标系下与LAO'和LPP'的对应关系如图22所示,其中LAO'为各展向截面的平均值。在ξ-η坐标系下,不同LPP'下所对应的最佳LAO'=-0.10~-0.15,即串列转子前后排叶片在弦向上略微有所重叠时性能最佳。此外,转子的失速压比受LPP'的影响不大,但峰值效率会受到LPP'的影响,LPP'越高,最佳LAO'下转子的峰值效率也越高。综上所述,前后排叶片在其弦向上有0.10~0.15倍弦长的重叠,可以获得较好的气动性能。
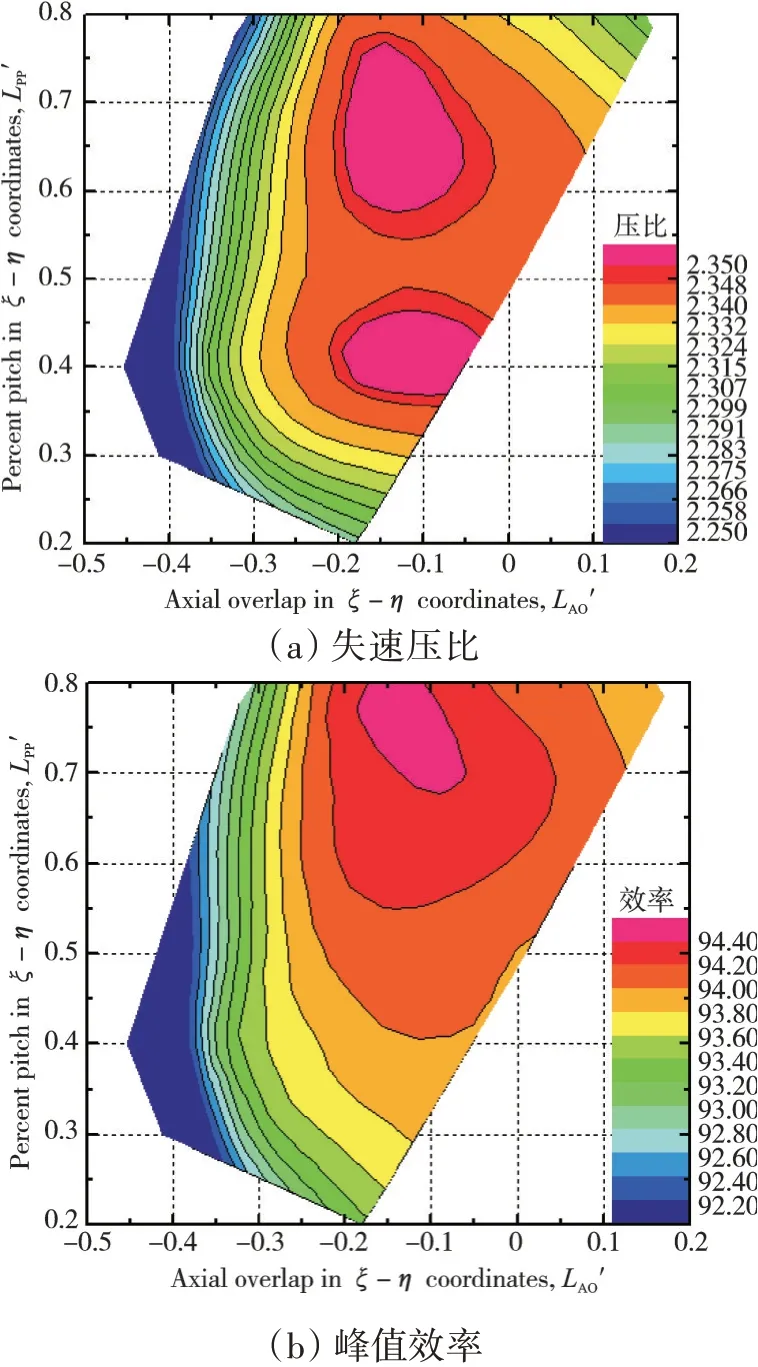
图22 在ξ-η坐标系下,串列转子失速压比、峰值效率随LAO'和LPP'的变化规律
2.2.2 超声速串列叶型优化设计
以跨声速串列转子叶尖基元流动为背景,在开展最佳相对位置和匹配工作规律分析的基础上,对来流马赫数为1.2时的串列叶型完成了优化设计,所选取的叶型为串列转子叶尖基元截面,其前后排相对位置、总稠度、进/出口几何角都是串列转子叶尖的典型值,优化过程中保证了上述参数基本不变。
在典型工作状态下超声速串列叶型的流场结构如图23所示。分析发现设计点前排通道正激波强度较大且位置靠后,吸力面一侧相交于尾缘附近,直接控制激波难度较大;而压力面一侧相交于50%弦长附近。基于以上流场特点,在压力面前50%弦长构造“内凹”型线,通过1组压缩波系降低通道激波强度,可调整的几何设计参数包括中弧线/厚度分布形式、前后排负荷分配等。后排在缝隙射流的加速作用下诱导出吸力面局部正激波,进而诱发了边界层的分离,为了控制后排吸力面激波强度,需要控制后排吸力面型面,以实现气流平缓加速。
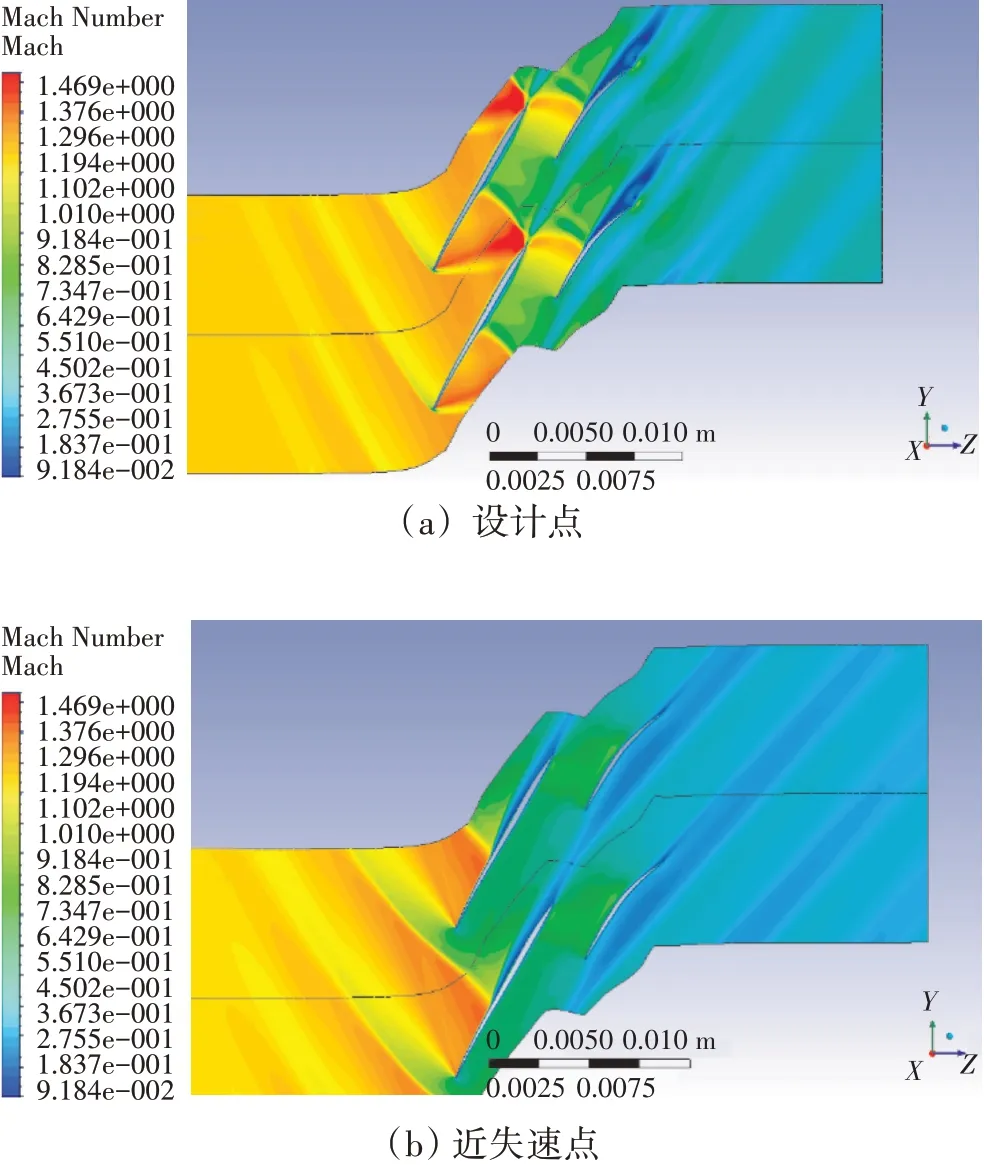
图23 在典型工作状态下超声速串列叶型的流场
综上所述,超声速串列叶型优化设计的核心问题是复杂激波系的控制,即前排弓形波、通道激波、后排吸力面激波强度的合理匹配。基于上述优化思路,在基准叶型的基础上主要调整如下:
(1)调整前后排弦长,以调整前后排负荷分配;
(2)调整前后排中弧线,以降低前排槽道正激波和后排吸力面激波的强度,提高前排弓形波强度;
(3)调整后排设计攻角,以适应缝隙射流诱导的局部攻角变化及吸力面加速。
静压比-损失特性、攻角-损失特性数值计算对比如图24所示。从图中可见,优化后设计点基元损失减少了20%,最小损失减少了6.5%,同时可用攻角范围拓宽了约0.5°。设计点、近失速点的流场和壁面等熵马赫数分布分别如图25、26所示。从图中可见,优化方案的激波强度分配更加合理,前排槽道正激波减弱,激波角减小;后排吸力面局部加速更加平缓,吸力面激波减弱;前排弓形波激波角增大。总之,优化方案在保持前后排相对位置、弯角分配基本不变的条件下,基于中弧线、弦长、局部攻角的修正进一步提升了叶型性能。基于流场特征的分析及优化设计结果表明,跨声速串列叶片激波强度的合理匹配对于调控负荷沿流向的分配、减少流动损失、改善叶型性能具有重要意义。
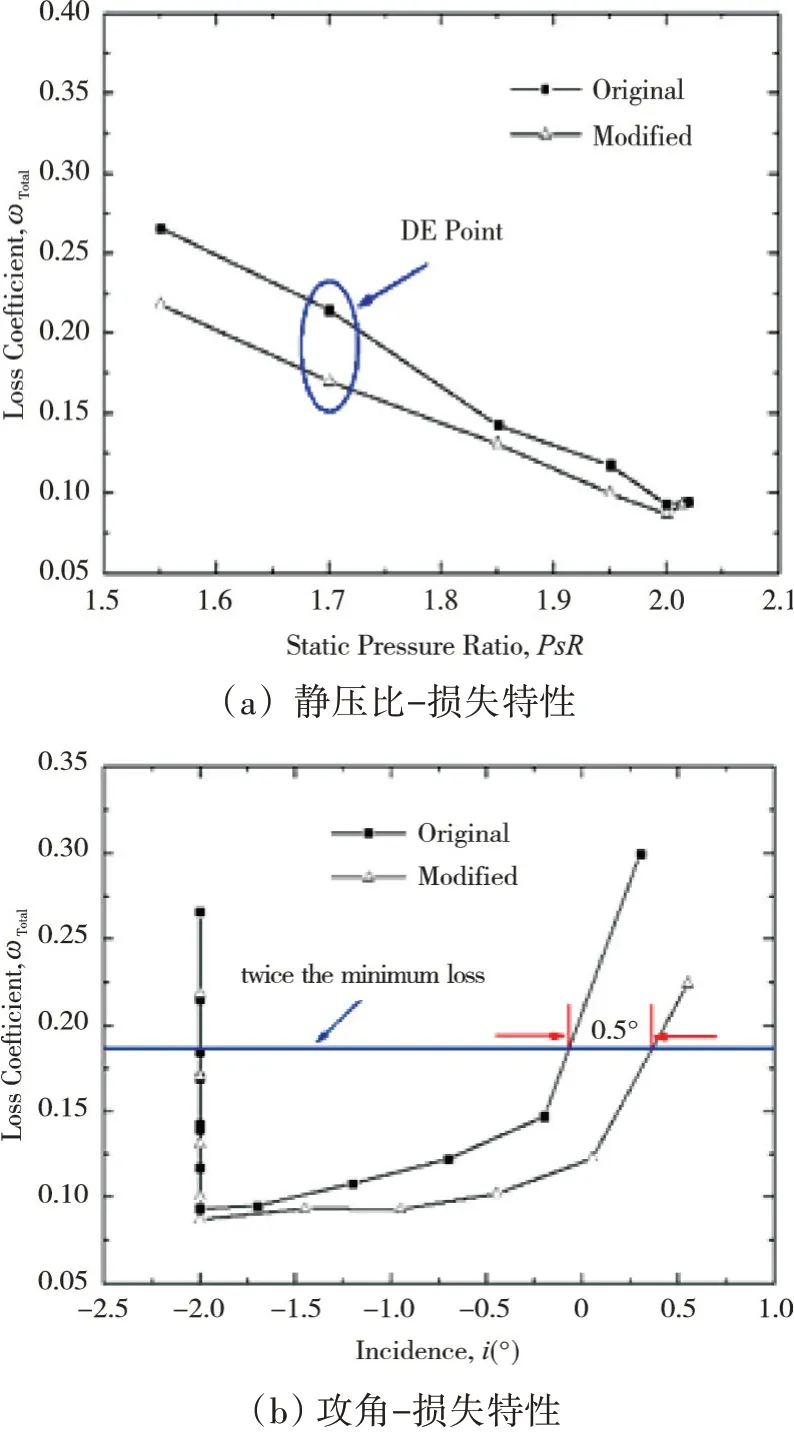
图24 优化前后叶型的静压比-损失特性、攻角-损失特性对比
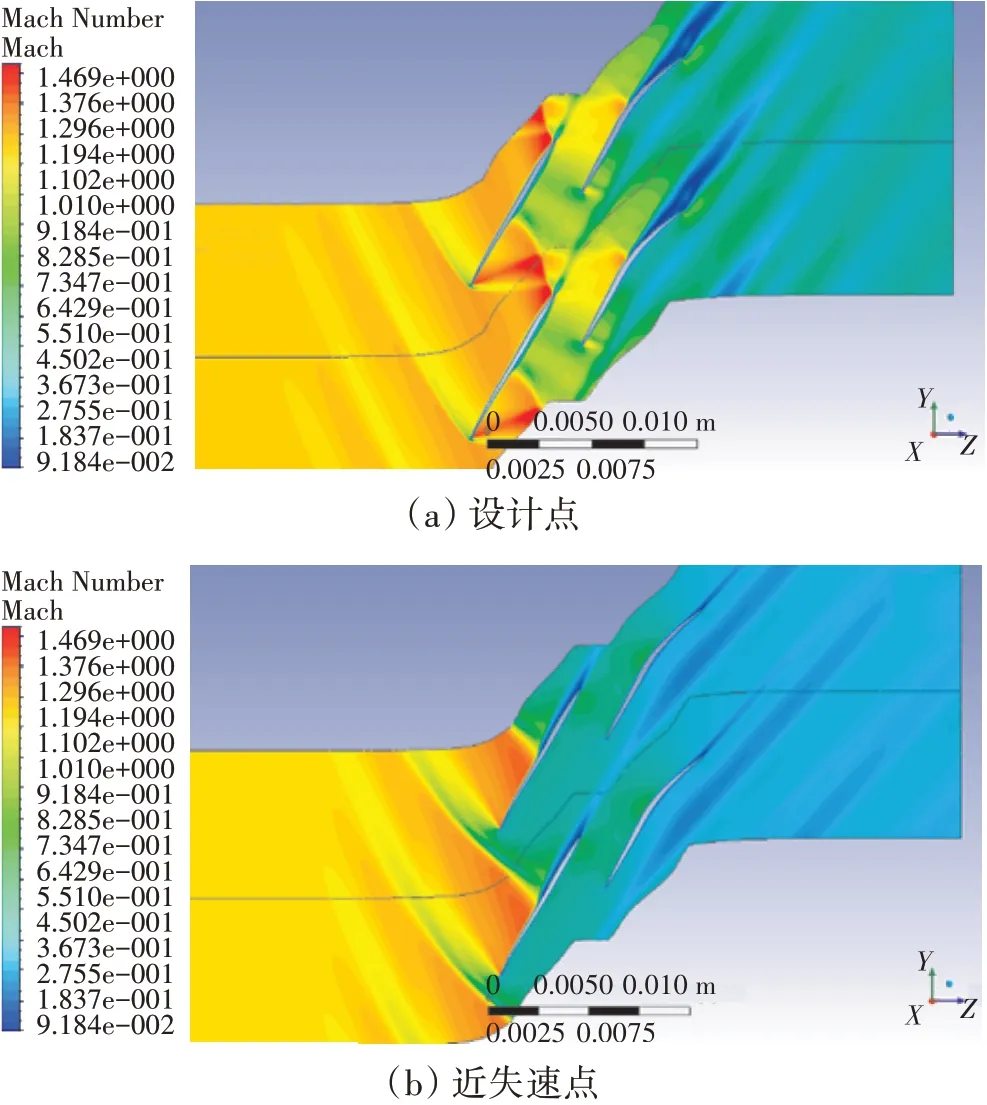
图25 优化方案设计点、近失速点马赫数分布
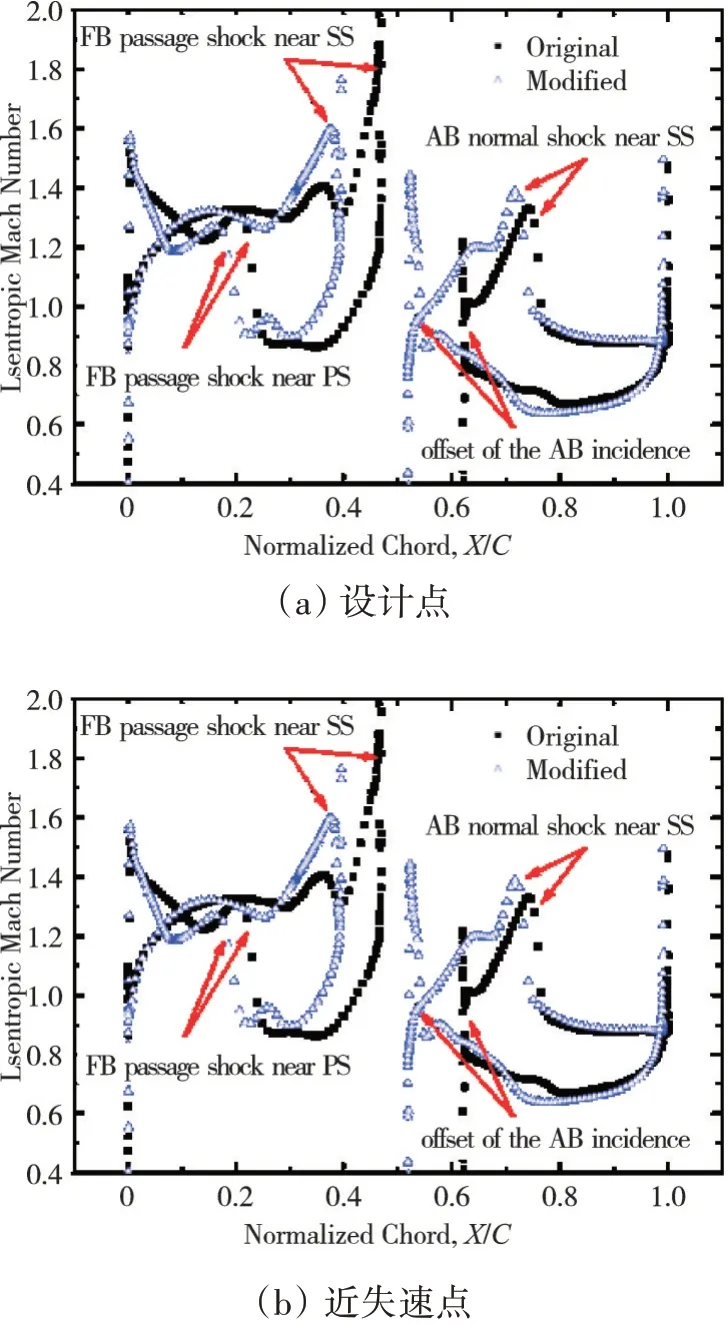
图26 原型与优化方案设计点、近失速点壁面等熵马赫数对比
3 跨声速高负荷串列叶片压气机方案设计
利用所发展的串列叶片设计技术,针对下一代风扇/压气机负荷系数高达0.40~0.45的实际需求,进行串列叶片出口级的双级风扇方案设计论证。作为参照,在结果中列出了1个2级常规叶片风扇的数值计算结果,串列叶片方案与2级常规方案共用进口级转子,在保证效率、裕度不变的条件下,串列方案出口级负荷系数从0.38提升至0.40,提升约5%。
论证方案的常用转速性能如图27所示。效率特性包含4条曲线,其中:Con.Ref为常规方案,Tan.Org为串列原型方案,Mod1在Org方案基础上优化的串列转子叶型,Mod2在Org基础上优化的串列静子叶型。从图中可见,在常用的转速范围内,出口级串列方案失速压比均高于常规方案,即在保证失速裕度为20%的条件下,出口级串列方案设计压比提高了4.5%,且中低转速堵点流量高于常规方案的,验证了高负荷条件下串列叶片的性能优势。
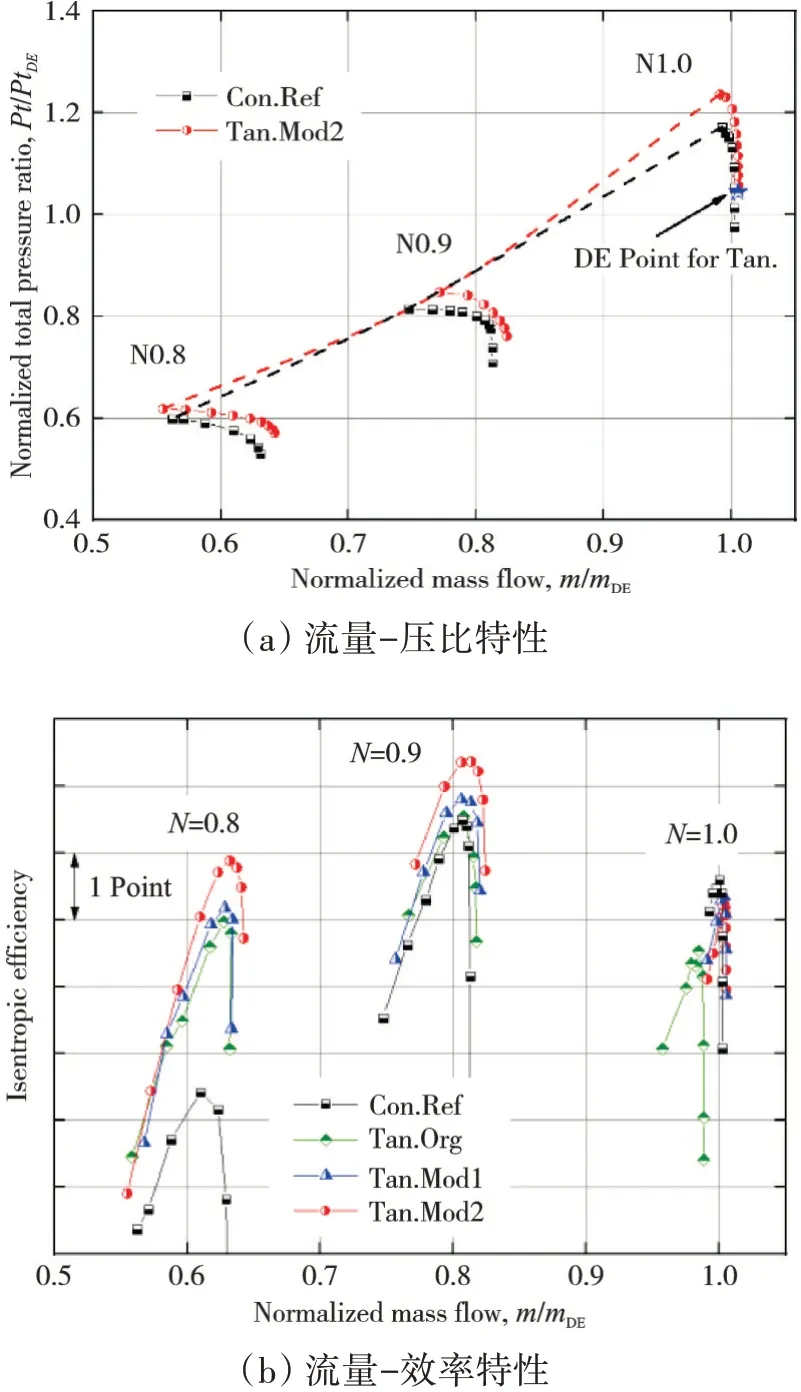
图27 论证方案的常用转速性能
Tan.Org的设计转速效率相比于常规方案的偏低,中低转速效率提升明显;Mod1的设计转速全工况范围内的效率相比于Org的提高了1.5~2.0个百分点,这主要是由于串列转子叶型优化改变了设计点激波系的空间分布(如图28所示),优化后串列转子3维激波面更加倾斜,且槽道正激波强度明显减弱,激波系强度分配更加合理,且吸力面低能流体堆积导致的低速区明显减小;Mod2的设计转速效率相比于Mod1的变化不明显,但转速为0.8时效率提升了1~2个百分点,这主要是由于串列静子叶型优化提高了叶型的负攻角范围,优化后在转速为0.8时的堵点串列静子堵塞状态明显改善(如图29所示),前排通道截止激波减弱,改善了中低转速下进/出口级匹配不协调的问题。综上所述,以本文发展的串列叶片设计理论及叶型优化技术为基础,所设计的串列叶片出口级的双级风扇全转速范围内失速压比高于常规方案的,在裕度保持不变的条件下,设计压比提高4.5%;设计转速效率与常规方案的持平,中低转速明显优于常规方案的,充分证明了高负荷条件下串列叶片的性能优势。
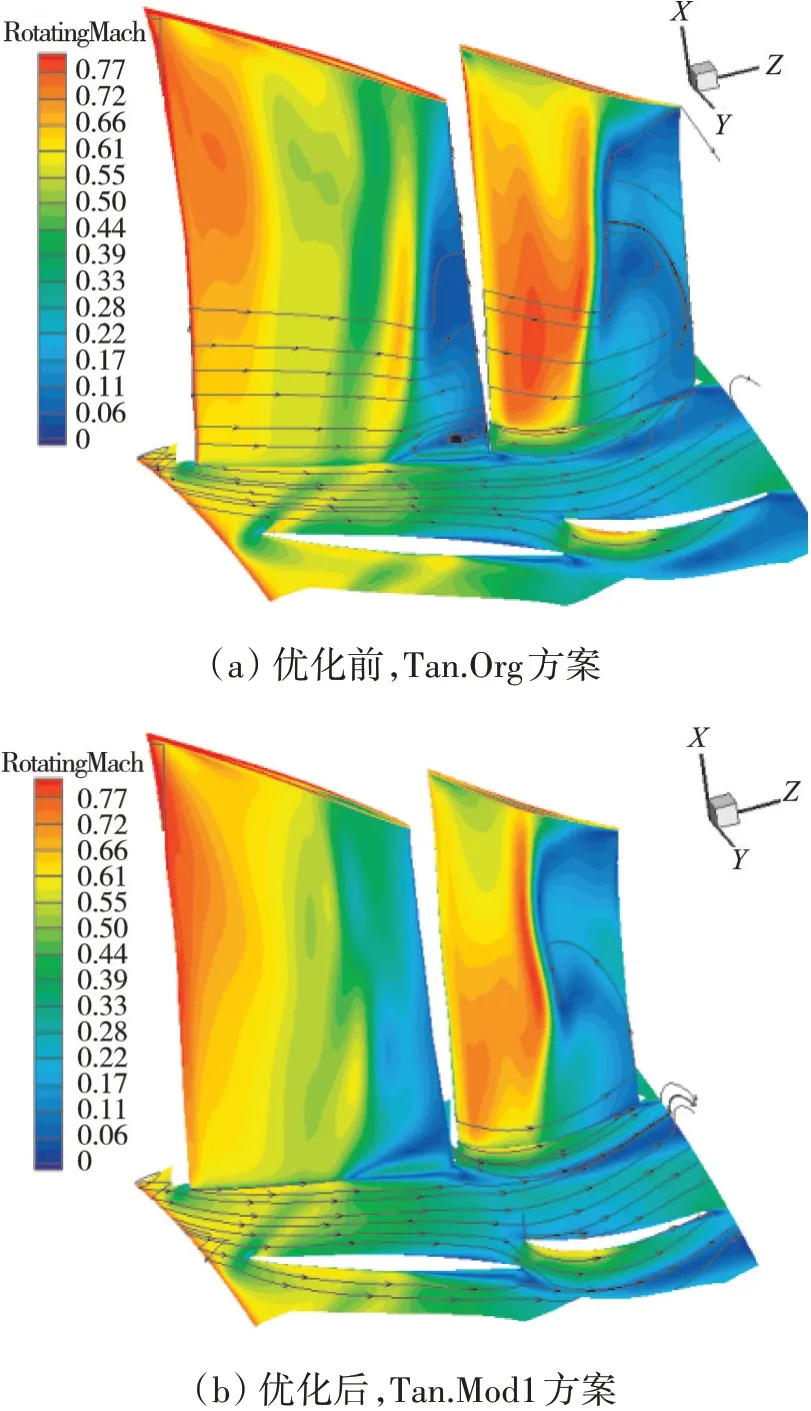
图28 在转速为1.0的设计点,串列转子叶型优化前后3维激波面及壁面流线对比
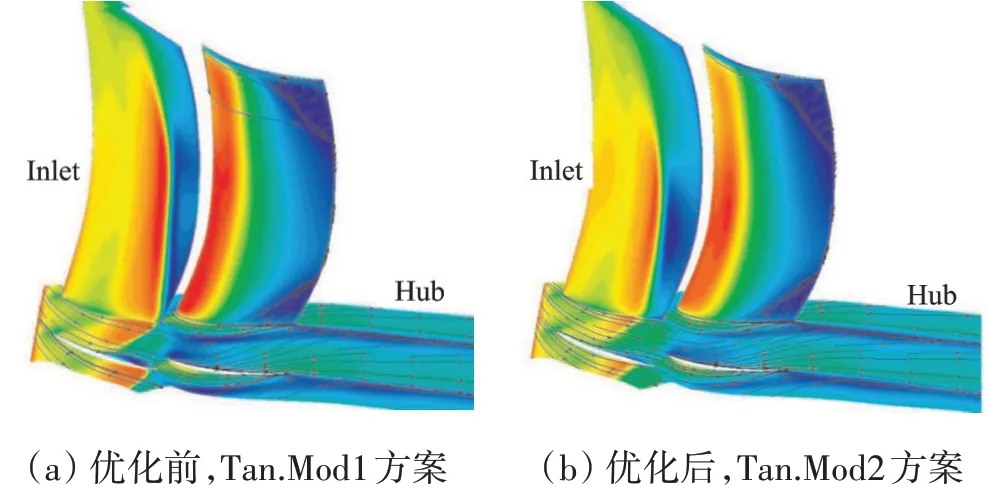
图29 在转速为0.8的工作点,串列静子叶型优化前后3维激波面及壁面流线对比
4 结论
(1)构建了串列叶片扩压极限理论分析模型,明确了串列叶片的负荷优势区间,并利用低速大尺寸压气机试验台验证了模型的正确性。其中,理论分析模型表明,串列叶片可以将常规叶片的扩压极限从约0.66提高到0.74;试验结果表明,当负荷系数大于0.46时,串列叶片表现出明显优势,可以将负荷系数为0.46作为串列叶片优势区间的临界点。
(2)开展了亚声速串列叶型设计技术研究,明确了势作用、缝隙射流、尾迹扩散主导下的前后排相互影响机制;发展了基于“中弧线修型”的亚声速串列叶型优化设计方法及其气动修型准则。数值计算结果表明,优化设计的亚声速串列叶型设计点损失减少6%,可用攻角范围拓宽2°。
(3)开展了超声速串列叶型设计理论与方法研究,总结了前/后排相对位置优选区间;明确了复杂激波系影响下串列叶型流动组织原则,以及前后排匹配工作规律。完成了典型超声速串列叶型的优化设计,数值计算结果表明,设计点损失减少20%,可用攻角范围拓宽0.5°。
(4)综合利用本文发展的串列叶片设计技术,完成了负荷系数为0.40的双级风扇串列叶片出口级气动方案设计论证,解决了串列叶片出口级设计转速效率偏低,以及在中低转速下与常规进口级难匹配的问题。数值验算结果表明,相比于常规方案,串列叶片出口级风扇设计压比提高4.5%,设计转速效率持平,中低转速等熵效率显著提高,初步验证了串列叶片设计的效果。
