初中数学教学中建模思想的渗透

摘 要：新时代初中数学教学改革中明确提出培养学生的数学核心素养，要将其作为初中数学教学的重要目标。本文将数学建模思想引入其中，通过创设数学问题情境，指导学生构建问题模型，引导学生通过观察、分析、推测等方法来进行学习和探究活动，从而培养学生的数学思维能力和逻辑抽象能力。

关键词：初中数学教学;建模思想;数学核心素养

中图分类号：G427                       文献标识码：A                    文章编号：2095-624X（2021）06-0037-02

引 言

数学模型是在实际教学过程中教师为了解决某个问题，对现有某个结构或其他研究对象展开分析研究，并将数学知识和方法作为工具对其进行重组和改造，最终构建成一个符合目前教学要求的数学结构[1]。由此可以看出，构建数学模型并不是随意地将公式定理展示出来，而是要从题目中各种已知变量出发，通过定性和定量的分析，再将已知条件进行整合，构建模型，并在最后问题解决的过程中，来验证模型的有效性。

一、由易到难建构数学模型，培养学生的模建模思想

数学模型的建构实际上是一个非常复杂的过程，教师要将题目中多种不同的已知条件和要求整合起来，指导学生进行分析。对于刚从小学进入初中的学生来说，因为他们很少涉及数学建模，所以在这一方面比较欠缺。基于此，在培养学生数学建模思想的过程中，教师要以最简单的数学建模为起点展开教学。首先，教师应从生活中常见的情境入手，指导学生结合基本的概念和公式来探索模型建构的路径，从最简单的生活问题入手，让学生感受利用模型解决数学问题的高效性，培养学生的模型建构思想。随后，教师逐步深化模型，提高模型的深度，培养学生的建模能力。

例如，在讲授人教版初中数学七年级上册“实际问题与一元一次方程”一节时，教师设计了这样一个问题：当地的玩具超市中有一件玩具商品的标价为150元，在春节来临之际，超市为了提高自身竞争力，开展了所有玩具八折起出售的活动，该活动开展后超市老板的实际利润变为20%，请学生计算该玩具的进价是多少元？初次解决这个问题时，大部分学生直接用150乘以80%得出八折后玩具的价格，随后根据利润的20%这个已知条件来计算出玩具的进价。在这个解决问题的过程中，学生仅处于一种模仿的状态。初中数学阶段，关注利润和进价的应用题比较常见，因此教师不妨借此题来培养学生构建数学模型的思想。

首先，分析已知条件，提炼出条件中的关键信息，如玩具标价为150元，活动期间八折出售，最终获利20%。利润率指的是标价减去进价的差，再除以进价。利润率模型是一个和生活息息相关，且非常简单的数学模型，学生根据这个模型来解决数學问题，可以让问题解决思路更加清晰明了。学生设玩具的进价为x元，根据建构的模型列出方程式：（150×0.8-x）/x=20%，从而得出正确答案。该问题就是应用一元一次方程解决实际问题，题目中所呈现的内容非常直观，学生也很容易把握已知条件，展开模型的构建。随后，教师可以再展示一些与之相关但比较深入的问题。例如，在题目中增加另一个玩具的价格，活动时所打的折扣，以及超市能获取的利润是多少，要求学生求出两个玩具的进价之差。这时，学生需要再次对模型进行分析建构，由单个商品单价过渡到两个商品的单价之差，再对之前的学习进行深入探究。

二、紧扣问题重点，转化已知条件建构模型

在传统的初中数学教学过程中，教师往往会通过灌输式的讲授法来讲解知识，让学生结合公式来解决问题[2]。久而久之，学生就形成了尊重知识权威、死记硬背的学习习惯，通过模仿来应用公式，概念和定理以解决问题，不利于培养学生的思维能力。新时代初中数学教学中，教师要打破以往的教学束缚，将认知提高和能力发展作为教学的重心。在讲授一些比较深奥、难以理解的知识时，教师可以采取多种不同的问题表征形式来对知识进行表征，如图象、表格等，让已知条件变得更加清晰直观，实现对复杂的知识进行梳理的目标，有助于学生更好地把握建模的方法。

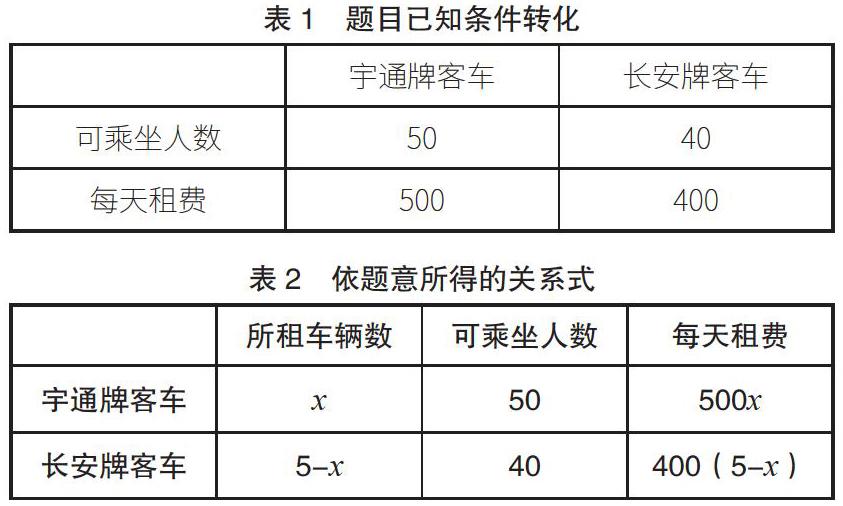
例如，人教版七年级下册“一元一次不等式”这节课要求学生在了解不等式解答技巧的前提下，掌握利用不等式解决实际问题的方法。教师展示了这样一道应用题：当地的公交公司有宇通牌和长安牌两种客车出租，其中宇通牌客车的可载人数是50人，每辆车一天的租金为500元。长安牌客车可载人数为40人，每辆车一天的租金为400元。我校下周将组织学生参观科技展览会，计划要租的客车数量为5辆。教师让学生根据实际情况解决以下问题：如果控制租金花费在2100元以下，最多可以租多少辆宇通牌的客车？目前参观科技馆的师生一共有200人，如果要控制租金在2100元以下，请设计出几种不同的租车方法，并找出最省钱的一种。这道题是对一元一次不等式的应用，从题目分析来看，该题的已知条件过多，有一定的难度。学生仅通过看的方式来分析题意，很容易在脑海中形成分散的知识点，不利于建模工作的展开。教师向学生讲授如何利用表格来转化已知条件。根据分析结果，学生设所租的宇通牌客车数量为x，并整理信息列出了表1和表2。

表1和表2所展示的已知条件和数量关系非常清晰，学生可以列出租金总额的方程式：500x+400（5-x）≤2100。学生按照一元一次不等式解法展开对算式的解答，得出不等式的取值范围后，可以知道x能够取的整数值是哪些，并根据所建立的一元一次方程式模型来得出最省钱的租赁方案。

三、模型归类思想传输，把握建模方向

随着对初中数学知识的深入学习，学生可以发现初中数学模型有很多种，如几何模型、方程式模型、函数图象模型、数据分析模型，等等。面对不同的数学问题，学生要根据实际情况来开展建模活动。但在实际学习中，大多学生很难把握建模的方向，难以灵活运用所学知识。因此，在教学过程中，教师应注重对建模方法的讲解，以培养学生灵活建模的能力。

例如，在讲授人教版初中数学八年级上册“全等三角形的证明”时，学生需要掌握五种不同的全等三角形的证明方法，分别是SSS、SAS、ASA、AAS、HL。在指导学生进行数学建模时，教师可用以实践操作为主的几何建模法，为每位学生分发一盒小木棒和橡皮筋。教师先要求学生分出两组小木棒，每一组小木棒中有3根，第一组小木棒的名称为a、b、c，第二组小木棒的名称为a'、b'、c'，要保证木棒之间的a=a'，b=b'，c=c'，然后利用橡皮筋将每组的三根小木棒固定成两个三角形，由此学生发现两个三角形全等，证明了SSS是判定两个三角形全等的定理。随后，学生让两组小木棒中a=a'、b=b'，但是c不等于c'，同样将两组小木棒分别组合成两个三角形，也可以发现两个三角形全等，因此证明了SAS也是判定两个三角形全等的有效方法。

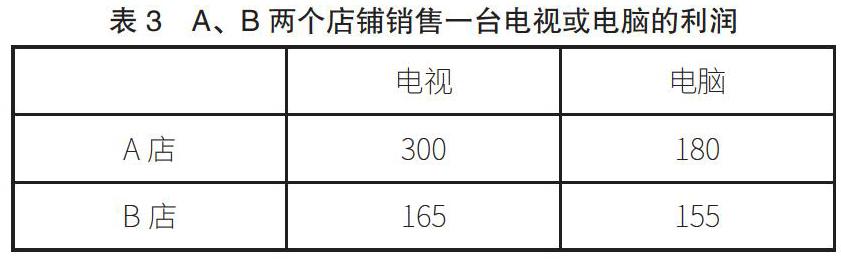
又如，在学习“一次函数”知识时，教师给出一道题目：批发商有50台电视和70台电脑，计划批发给A、B两个电器专卖店，其中80台分给A店，40台分给B店，已知A、B两个店销售电视和电脑的利润分别如表3所示。假设分给A店电视为x台，将这120台电视和电脑全部卖出后利润一共为多少？

要解决这道题，学生需要建立的模型为函数模型。教师指导学生分析得出，分给A连锁店的电脑为（80-x）;分给B店的电视为（50-x），电脑为（x-10）。最后可列出函数模型：y=300x+180（80-x） +165（50-x）+155（x-10）。

针对不同的数学问题，教师要有针对性地指导学生进行分析，通过辨析题意，抓住题目中的已知条件和关系式，厘清题目的思路，指导学生选择合适的解题方法，让学生利用正确的数学模型来解决问题，以培养学生的思维能力[3]。

结 语

初中数学建模教学是初中数学教學的重要组成部分。在初中数学教学的过程中，教师应抓住建模教学的要求，紧扣问题，指导学生分析题意，理解题目中的已知条件和问题，选择适合的数学建模方法，最后正确解答问题。同时在建模教学过程中，教师要以学生为主体，让学生以合作探究形式进行建模。

[参考文献]

邹翠芳.基于建模思想的初中数学实践与反思[J].中学数学，2020（12）：88-89.

游康生.基于建模思想的初中数学实践与反思[J].当代教研论丛，2019（09）：74+79.

刘增寿.初中数学建模教学的策略分析[J].名师在线，2019（29）：35-36.

作者简介：黄求滨（1991.6—），男，广东潮州人，本科学历，专业技术十一级，研究方向：初中数学教学。