后装式压缩垃圾车翻转机构转臂轻量化
2021-08-26秦东晨胡朋磊王婷婷何寄平
秦东晨,胡朋磊,王婷婷,何寄平
(1.郑州大学机械工程学院,河南 郑州 450000;2.郑州宇通重工有限公司,河南 郑州 450000)
1 前言
生活垃圾的处理作为环境保护不可或缺的一环,在垃圾处理中垃圾车得到了广泛的应用,后装式压缩垃圾车[1]便是一种常见的压缩运输工具。翻转机构在后装式压缩垃圾车起到上料的作用,其三维模型,如图1所示。其运动原理为油缸驱动转臂转动,转臂、拉臂及挂桶架组成刚体导引机构实现对垃圾桶的翻转。为了提高后装式压缩垃圾车的动力学及续驶里程,且为以后对整车轻量化提供理论依据,对翻转机构转臂进行轻量化研究。目前,对压缩垃圾车上料机构的研究相对较多,但大多是对上料机构进行动力学研究或者拓扑优化。文献[2]通过建立侧装式垃圾车机械手的虚拟样机模型对侧装式垃圾车机械手进行动力学分析,并在典型工况下进行静强度刚度校核,最后在Workbench中以各部位厚度为设计变量,根据迭代计算对机械手进行了尺寸优化,达到减重的目的;文献[3]对压缩式垃圾车翻桶功能化虚拟样机进行了参数化设计,选取六个坐标值为设计变量,对翻桶机构进行优化分析,使得上料过程更加平稳,液压系统工作环境得到有效改善;文献[4]运用LMS Test Lab对农用车架进行模态试验,得到相关模态参数验证有限元模型的正确性,以第二阶频率为目标函数,基于变密度法进行拓扑优化,对防止车架共振提供了较高的工程实用价值;文献[5]在疲劳载荷下以疲劳寿命为优化目标,基于变密度法对麦弗森控制臂进行了拓扑优化,对拓扑优化的模型进行重构,设置参数,进行灵敏度分析和尺寸优化,使控制臂在满足疲劳寿命的情况下进一步进行了减重;文献[6]对拉臂式垃圾车的拉臂机构进行动力学分析,得到铰点载荷建立有限元模型,对拉臂进行结构改进,基于导入准则法对拉臂进行结构优化,得到出色的减重效果。文献[7]提出一种基于拓扑优化与响应面法相结合的轻量化设计方法,首先对光伏板清扫机器人支撑架进行离散拓扑优化,选取设计变量,进行试验设计,建立二阶响应面模型,基于非支配多目标遗传算进行迭代计算,使支撑架实现了轻量化及增加结构强度。

图1 后装式垃圾压缩车翻转机构三维模型Fig.1 Three-Dimensional Model of Rear-Loading Garbage Compression Truck Flip Mechanism
考虑到转臂在最差工况下的受力情况,翻转机构的加工工艺以及成本问题,对高强度钢材质的翻转机构转臂进行结构优化,首先建立虚拟样机及有限元模型,将仿真结果与实验对比验证模型的正确性;采用基于SIMP变密度法的拓扑优化和基于全局响应面法的形状优化相结合的优化方法对转臂进行轻量化研究,得出基于拓扑优化的更优化方案。
2 动力学仿真
对机构进行动力学仿真,可得到零件的典型工况,以便对零件进行进一步的研究。文献[8]建立了厨余车提升翻转机构的虚拟样机模型,仿真求得油缸最大推力大小及所处位置,为以后的静力学分析与模态分析提供了依据。将三维模型转换为X_T格式文件,导入Adams软件,对模型添加约束,定义材料属性,垃圾桶重量设置为600kg,建立翻转机构的虚拟样机模型,如图2所示。转臂与挂桶架、转臂与油缸、拉臂与挂桶架以及转臂、拉臂、油缸与车身均为旋转副连接,由于翻转机构左右对称,故采用一个移动副驱动的方式。根据油缸实际驱动过程,设置位移驱动为12mm∕s,结束时间为20s,仿真步长为0.1,仿真得转臂与油缸的旋转副(旋转副A)受力曲线及转臂与挂桶架旋转副(旋转副B)受力曲线,如图3所示。由图3可知在16.0s旋转副A受力即油缸驱动力最大为92442.08N,此时旋转副B受力X方向为13259.23N,Y方向为-40019.33N。另外由旋转副B与转臂与车身的旋转副(旋转副C)的转角曲线可知旋转副B转角为47.20°,旋转副C转角为7.38°。

图2 翻转机构虚拟样机模型Fig.2 Virtual Prototype Model of Flip Mechanism

图3 转动副A、B受力曲线Fig.3 Force Curves of Rotating Pairs A and B
3 模型验证
根据对翻转机构进行动力学仿真的结果,可得翻转机构的最差工况受力情况及最差工况翻转机构所处位置。将三维模型转换为STEP格式文件导入HyperMesh中,删除与分析无关的零件,将翻转机构旋转至最差工况位置,划分网格,检查网格质量,添加属性、约束及边界条件,根据动力学仿真结果,对有限元模型添加载荷,得出转臂最大应力值及位置,与所搭建试验台的实验结果进行对比,验证虚拟样机模型及有限元模型的正确性。转臂有限元模型及应力云图,如图4所示。试验台转臂及应变片所测得的应力曲线,如图5所示。由试验台实验结果得知两转臂内圆转角处应变片最大应力分别为341.66MPa和369.40MPa,平均应力为355.53MPa,有限元分析结果为367.30MPa,误差为3.2%,说明所建虚拟样机模型及有限元模型符合实际情况,误差原因主要为试验台装配误差。转臂所用材料为高强度刚HG785,最大许用应力为785MPa,设计安全系数为1.5,得许用应力为523.33MPa,由仿真和实验结果可得转臂具有较大减重空间。
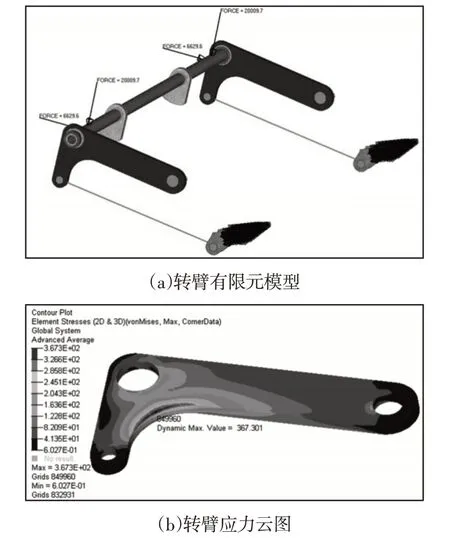
图4 转臂有限元分析Fig.4 Finite Element Analysis of Rotary Arm
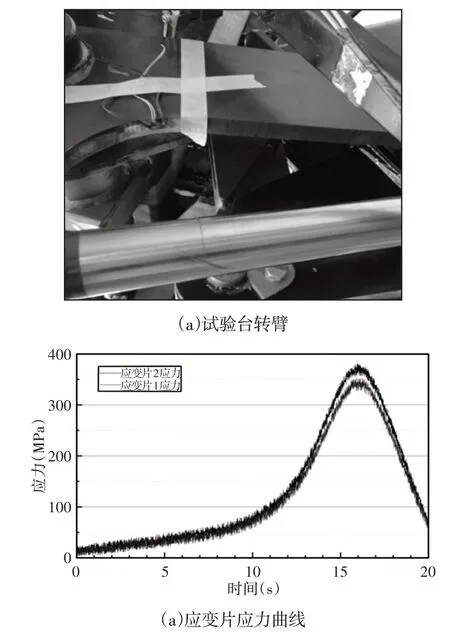
图5 试验台转臂及应力曲线Fig.5 Rotary Arm of Test Bench and Stress Curve
4 拓扑优化
基于HyperMesh的OptiStruct求解器,采用SIMP变密度法对转臂进行拓扑优化,拓扑优化包括设计变量、约束条件和目标函数三要素,其数学模型[9]如下所示。

式中:X—单元密度矩阵矢量;U—单元节点位移矢量;K—结构整体刚度矩阵;v i—初始模型每个单元体积;v j—优化模型每个单元体积;V0—初始模型体积;η—体积分数约束值。
拓扑优化的转臂模型,如图6所示。将转臂模型划分为设计区域和非设计区域,拔模方向设置为翻转机构的轴向,以转臂静态应变能为优化目标,约束为体积分数取0.3,对转臂进行拓扑优化。

图6 拓扑优化的模型Fig.6 Topology Optimization Model
经过25步迭代,结果收敛,目标函数迭代曲线及拓扑优化结果,如图7所示。将拓扑优化结果在OSSmooth功能中导出为X_T格式文件,在三维软件中对模型进行改进,得到平滑的模型,如图8所示。导入HyperMesh中重新划分网格,建立有限元模型进行静力分析,应力云图,如图9所示。改进模型质量9.56kg,静力分析得最大应力455.082MPa,满足最大应力要求。为了实现更为精确的尺寸和优化设计,还需要对改进模型进行形状优化。

图7 拓扑优化结果Fig.7 Topology Optimization Results

图8 改进模型及形状变量Fig.8 Improved Model and Shape Variable

图9 改进模型应力云图Fig.9 Stress Cloud Diagram of Improved Model
5 形状优化
5.1 建立参数及试验设计
建立形状优化[10]的参数,首先针对转臂的实体网格建立do⁃mains和handles,在HyperMorph中对要进行形状优化的边线的法向位移量创建形状变量,七个形状变量的位置,如图8所示。根据改进模型的应力云图可得转臂未达到最大许用应力要求,故将七个形状变量预定义为向外方向,位移量设置为6mm,初始量为0mm,所有形状变量下限均为-0.2,shape1、shape5、shape6上限为1.2,shape2、shape3、shape4上限为1.5,shape7上限为1.7。将形状变量导出为shp格式文件,在HyperStudy中首先将模型编辑为tpl格式的模板文件,新建study导入形状变量、体积响应与应力响应,在这里需注明所建体积响应为整个有限元模型的体积,并非转臂的体积,不影响后续优化计算,点击Evaluate tasks,success表示HyperStudy与HyperMesh计算文件成功创建关联。在进行优化之前,需要进行试验设计,目的是通过试验设计得出形状参数对响应的主效应[11]影响,从而筛选出对目标响应不敏感的参数,缩短开发周期,而且通过试验设计可以评估形状变量的设置范围是否合理,如果不合理,在试验设计过程中会报错。由于形状变量较少,选择2水平的全因子试验设计方法,经过128步计算得到形状变量与响应的试验样本,变量对响应的主效应,如图10所示。由图10可知shape2、shape3、shape4、shape7对应力响应不敏感,但所有变量对体积响应都敏感,并且形状变量较少,所以不再筛去变量。

图10 变量对响应的主效应Fig.10 Main Effect of Variables on Response
5.2 优化求解
在HyperStudy中创建优化,以体积响应最小为优化目标,应力响应为约束,采用全局响应面法[12](Global Response Surface Method,GRSM)对转臂进行结构优化,设置迭代步最大为80,约束设置为523.33MPa,经过37步迭代达到收敛,目标函数迭代曲线,如图11所示。各形状变量优化结果,如表1所示。shape2、shape3、shape4对应力影响不大,所以寻优结果为上边界,优化前后最大应力值及重量对比,如表2所示。拓扑优化结果相比现有结构减重了46.3%,形状优化在拓扑优化的基础上又减重了18.3%。
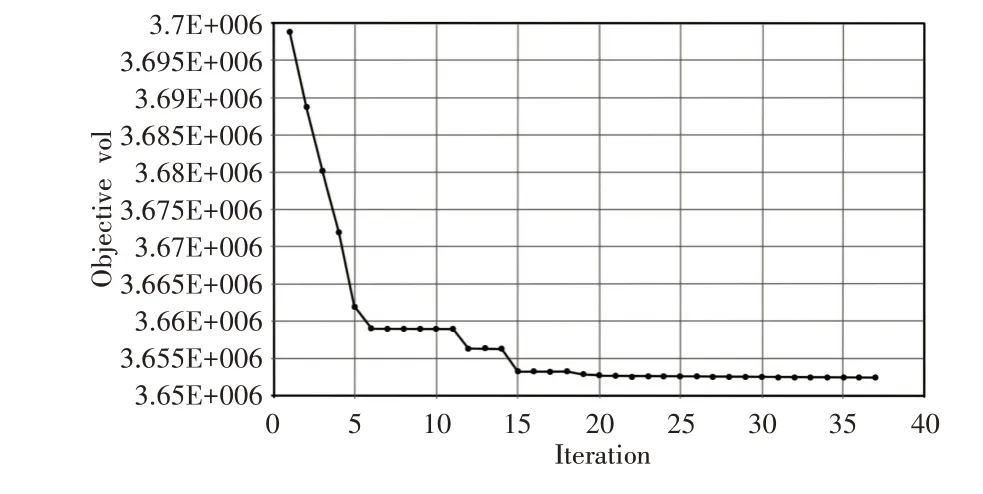
图11 形状优化目标函数迭代曲线Fig.11 Iterative Curve of Shape Optimization Objective Function

表1 形状变量优化前后对比Tab.1 Contrast before and after Shape Variable Optimization

表2 优化前后对比Tab.2 Contrast before and after Optimization
6 总结
(1)建立后装式压缩垃圾车翻转机构的虚拟样机模型以仿真求得运行最差工况,通过有限元分析求得最大应力,与试验台实验结果对比验证虚拟样机模型及有限元模型的正确性。
(2)基于SIMP变密度法对转臂进行拓扑优化,对拓扑优化后的结果重新设计,拓扑优化模型与原始模型相比减重46.3%。
(3)基于拓扑优化后的转臂,确定形状参数,进行试验设计,采用全局响应面法对新转臂进行形状优化,使形状优化模型在拓扑优化模型的基础上再减重18.3%,对翻转机构的轻量化研究具有一定的工程意义。
