玄武岩及其混合料断裂性能浅析 *

2021-08-26陈升平李航宇张建波

陶瓷 2021年7期

田肖陈升平李航宇张建波

(湖北工业大学建筑与环境学院武汉 430068)

前言

混凝土作为当今世界上最常用的工程材料,在外界条件影响下常常产生裂缝。大部分的裂缝不会对建筑物的正常使用有所影响,但会减少结构的使用寿命。在普通混凝土里掺入纤维，可有效改善混凝土的这些不足。混掺多种纤维能使纤维相互协调，相互弥补，可更好的提高混凝土结构的韧性和使用寿命。笔者选用的钢纤维和玄武岩纤维的材料性质有很大差异，因此将不同性质和尺寸的钢纤维和玄武岩纤维混杂掺入混凝土后，二者将会发挥协同作用。目前有两种材料参数可用于估计纤维混凝土的增韧效果。一种是纤维混凝土的断裂韧度，另一个是纤维混凝土的断裂能。由于试验中的裂缝宽度远小于所使用纤维的长度，且断裂能又与纤维拔出和脱粘密切相关，所以在纤维混凝土结构或构件的设计过程中，断裂能的作用是非常有限的。因此，设计者往往会关心基体开裂后在允许的裂缝宽度范围内(如0 mm～2 mm)拉应力与裂缝宽度的关系。这一关系可以由直接拉伸法来获得，但是试验难度过大，现在主要使用三点弯曲得到的P-CMOD曲线结合反分析法来获得。

近年来，大量国内外学者都对纤维混凝土断裂特性进行了研究。罗素蓉，林扬兴[1]等人通过三点弯曲梁断裂试验得出，在体积掺量为0.2%的PVA纤维与体积掺量为1.0%的钢纤维混杂时混杂效应较优，对高强混凝土各项断裂性能的改善效果最为理想。

马银华[2]等人选用几种不同类形、不同规格的纤维，对带切口的单掺或混掺纤维混凝土试件进行了三点弯曲试验和数值模拟，并与素混凝土试件进行了对比。研究表明，普通钢纤维，超细钢纤维，PVA三元混杂纤维混凝土断裂能增加了1632%，断裂韧度增加了44.76%，临界裂缝张开位移增加了37.87%，且荷载与裂缝张开位移曲线更加饱满，峰值荷载后出现屈服平台现象，其中部分曲线在下降段甚至再次上升而出现了二次峰值现象，表现出良好的抗裂性能和韧性。

Ali Nour，Bruno Massicottc[3]等人利用反分析法，根据试验的荷载位移曲线，对钢纤维混凝土的拉伸软化曲线进行了研究，并将软化曲线近似为三折线，模形计算结果与试验结果比较吻合。

Stefie J. Stephen[4]等人采用多线性拉应力—裂缝张开位移软化曲线模形，结合全局优化算法，得出了载荷与裂缝张开位移曲线的最佳拟合参数，建立了由拉应力与裂缝张开位移曲线表示的拉伸本构关系。为研究钢—玄武岩混杂纤维混凝土的断裂特性，本文通过劈拉实验和三点弯曲实验得出了各组混凝土的劈拉强度和P-CMOD曲线，再结合双线性软化曲线模形，反分析建立了钢—玄武岩混杂纤维混凝土的双线性软化关系。

1 试验概况

1.1 原材料

(1)水泥：华新P.O42.5普通硅酸盐水泥；细骨料：级配Ⅱ区中砂，细度模数为2.5到3.0之间；

(2)粗骨料：粒径5 mm～20 mm，清洗后含泥量少于1%；

(3)粉煤灰：巩义市铂润耐火材料有限公司生产的一级粉煤灰；

(4)减水剂：聚羧酸高性能减水剂；

(5)水：普通自来水；

(6)钢纤维：华源金属生产的端钩形钢纤维；

(7)玄武岩纤维：海宁安捷材料生产的短切玄武岩纤维。

1.2 试验方案

按“普通混凝土配合比设计规程”制作尺寸为100 mm×100 mm×100 mm立方体试块，强度等级为C30的普通混凝土、钢纤维混凝土、玄武岩纤维混凝土以及钢—玄武岩混杂纤维混凝土，浇筑完成24 h后拆模，养护室养护28 d后测其抗压强度和劈拉强度，每组试验测试6个试件，共16组，合计96个。制作了100 mm×100 mm×400 mm钢—玄武岩混杂纤维混凝土梁，在跨度中央预制一条宽4 mm左右、深30 mm的裂缝，共48根，在微机控制电子压力试验机上进行三点弯曲试验。

2 混凝土断裂能和断裂韧度计算方法

2.1 断裂能

断裂能是计算双线性软化曲线参数的关键。一般采用荷载—挠度曲线图来计算混凝土的断裂能。但是在采用三点弯曲法获得混凝土梁的荷载—挠度曲线对伺服试验机以及试样的尺寸和试验加载装置要求较高。所以世界著名混凝土专家美国西北大学Shah教授提出采用P-CMOD曲线来代替P-δ曲线来近似计算断裂能的想法，并验证了这一想法。

混凝土梁在断裂过程中产生的断裂功W是由荷载P在跨中产生的弯矩M1和梁自重在跨中产生的弯矩M2组成。余啟春，陈红鸟将荷载P和转角θ为CMOD的函数，分别记为f(CMOD)和g(CMOD)，得出荷载所做的功为

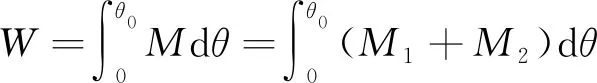
①

式中：CMOD0表示梁的旋转角为θ0时对应的裂缝口张开位移；m表示梁的质量；g表示重力加速度。

可以通过下式计算得出断裂能。

②

式中：Gf表示断裂能；P表示施加在试件上的总荷载；S表示试件梁的跨度；a0表示预制裂缝长度；D表示试件的高度；B表示试件的厚度；(D-a)B表示断裂面的投影面积；W表示总荷载所做的功。为能使断裂能的计算更加简便，本文通过关系式Y=a1X6+a2X5+a3X4+a4X3+a5X2+a6X+a7拟合P-CMOD曲线，然后代入式①，②。可计算得出各组试件的断裂能。钢—玄武岩混杂纤维对混凝土断裂能的增强效果显著且强于单掺纤维，具有良好的协同效应。当掺入定量的玄武岩纤维时，随着钢纤维掺量的增加，钢—玄武岩混杂纤维混凝土的断裂能也随之增加。当钢纤维掺量一定时，随着玄武岩纤维掺量的增加，钢—玄武岩混杂纤维混凝土的断裂能呈现先增后减的趋势。这是因为随着纤维掺量的增加，纤维之间就会结团，相互缠绕，在搅拌混凝土时会出现较大的孔隙，从而影响混凝土的断裂能。当钢纤维掺量为1.6%，玄武岩纤维掺量为0.1%时，钢—玄武岩混杂纤维混凝土的断裂能值最大为2 020 N/m。

2.2 断裂韧度

在Ⅰ形裂缝条件下，当混凝土的应力强度因子KⅠ达到临界值KⅠC时，裂纹发生失稳扩展，这个临界应力强度因子KⅠC称为断裂韧度，它也是用来表征混凝土断裂特性的重要参数之一。本文对比分析了各组混凝土的断裂韧度。混凝土断裂韧度采用美国材料与试验学会建议的断裂韧度KⅠC计算公式。

3 钢—玄武岩混杂纤维混凝土拉应变软化关系

3.1 双线性软化关系

在分析混凝土断裂行为时，软化曲线的形式是虚拟裂缝模形的重要内容。根据虚拟裂缝模形的假设，在拉应力作用下，混凝土的开裂及裂纹扩展过程中的本构关系如下：在非开裂区，开裂前、后均为线弹性的应力—应变关系。在开裂区采用非线性的拉应力—裂纹张开位移关系。这两种本构关系含有的材料参数如下：弹性模量E，抗拉强度和拉应力与裂缝张开位移关系，其中拉应力与裂缝张开位移关系即为本文所关注的软化关系。由于混凝土是一种准脆性材料，其软化曲线是一条复杂的光滑曲线，为了研究混凝土材料断裂特性的方便，国内外学者提出了各种简化的软化曲线形式，其描述函数包括线性函数、双线性函数、三线性函数、指数函数及幂函数等。

③

该模形只需要确定两个参数断裂能Gf和抗拉强度ft，这两个参数均能通过试验得出。

式中，σ1是转折点1处的应力值；w1转折点1处的裂缝张开位移；wc为临界裂缝张开位移。

3.2 数值模拟

本文采用ABAQUS来模拟混凝土的三点弯曲试验，利用反分析法确定双线性软化关系的参数。在反分析过程中，通过对比模拟的P-CMOD曲线与实测P-CMOD曲线在0 mm～2 mm之间围成的面积对软化参数进行一步步搜素，当模拟的P-CMOD曲线和实测曲线之间的离散值e达到最小的时候，所对应的值便为模拟的软化曲线参数，e的计算公式如下

④

式中Aexp和Anum分别是试验与计算得到的P-CMOD曲线与水平轴在0 mm～2 mm之间围成的面积。

建模时，网格划分起着非常重要的作用，它直接影响着计算的精度和运行的快慢。本文在网格划分时采用由密到疏的方式，使得远离裂纹处的单元网格相对稀疏，就可以确保计算结果在保证精度的前提下，有效减少有限元节点数目，进而加快运算速度。

对于钢—玄武岩混杂纤维混凝土，当掺入定量的钢纤维时，随着玄武岩纤维的增加，W1和Wc值也随之增大。

相较于普通混凝土，所有纤维混凝土的荷载—裂缝张开位移曲线都更加饱满。当钢纤维掺量一定时,随玄武岩纤维掺量的增大,钢—玄武岩混杂纤维混凝土试件的荷载—裂缝张开位移曲线与坐标轴的包络面积上大多数呈现增大的趋势。但当钢纤维体积率为1.6%，玄武岩纤维体积为0.15%时，混凝土的峰值荷载和荷载—裂缝张开位移的包络面积均小于钢纤维体积率为1.6%，玄武岩纤维体积为0.1%的混凝土。这是因为纤维掺量较高时,纤维会结团导致水泥浆液不足以完全包裹纤维而影响了混凝土的韧性。