基于状态相依风险厌恶的最优投资再保险策略*

李淑琦，赵永霞

(曲阜师范大学统计学院，273165，山东省曲阜市)

0 引 言

随着经济的高速发展，人们的财富水平日益提高，对保险的需求不断加大.目前，保险业总资产正在急速增长，拥有大量资产的保险人已经成为资本市场的主体，其面临的问题也越来越多.一方面，我国经济政策的相继出台使得保险资金投资渠道增加，这加大了资本市场的利率风险、股市波动风险和通胀风险，使得保险人面临更高的投资风险.另一方面，保险人的风险承担压力越来越大，为了控制保险风险，保险人选择开展再保险业务，其目的是将部分保险风险转移给再保险人.为了控制投资风险和保险风险，找到最优投资和再保险策略，许多学者开始研究最优投资再保险问题.

近年来，均值-方差准则下的最优投资再保险问题受到众多学者关注，Zeng和Li[1]基于扩散模型进行研究；杨鹏和刘琦[2]基于两种相依保险业务进行研究；Zeng等[3]在盈余过程和风险资产过程中均引入跳扩散项，研究一个风险资产时的结果；孟祥波等[4]将其拓展到多个风险资产.这四篇文献所考虑的都是比例再保险，针对超额损失再保险，Li等[5]基于谱负Levy过程进行研究.上述文献均考虑常数风险厌恶，研究结果显示最优策略与财富水平没有相关性，这一结果不符合常理.现实中，一个人的风险厌恶水平应该与他的当前财富水平有一定的关联，也就是说，风险厌恶依赖于保险人的当前财富水平.

考虑到上述原因，很多学者在引入状态相依风险厌恶的均值-方差准则下研究最优投资再保险问题.仅考虑投资时，Bjork等[6]根据 Bjork和Murgoci[7]的研究框架在扩散模型下进行求解；Zhang和Liang[8]则在两个跳扩散风险资产下进行讨论.既考虑投资又考虑再保险时，Li等[9]基于扩散过程和比例再保险在风险资产价格与盈余过程相互独立的条件下进行研究；Bi等[10]对其进行拓展，研究风险资产价格与盈余过程有相关性时的结果；Zhang等[11]则基于两种相依保险业务，分别在扩散风险模型和 Cramér-Lundberg (C-L) 模型下进行研究.结果显示，上述文献所得到的最优策略与保险人当前财富水平具有相关性，也就是说考虑状态相依风险厌恶使得结果更为合理.

本文将从风险模型和再保险方式两个方面对Bi和Cai[10]进行拓展，具体是考虑带有状态相依风险厌恶的均值-方差准则，拟在有泊松跳的风险模型中研究最优投资和超额损失再保险问题.从状态相依风险厌恶的角度看，本文也推广了Li等[5]中的结果.

本文结构安排如下：首先，对最优化问题进行阐述，建立带有状态相依风险厌恶的均值-方差模型，并给出风险厌恶函数；其次，求解最优化问题，得到最优投资再保险策略及相应的值函数；最后，用数值实例说明模型参数对策略的影响.

1 模型介绍

(1)

定义1.1 策略u=(πt,l(z,t))t∈[0,T]称为可允许策略，如果它满足下列条件：

(1)u是F-循序可测的；

(2)对任意t∈[0,T]和z≥0，πt≥0,0≤l(z,t)≤z;

(3)对任意(t,x)∈[0,T]×，

(4)对任意(t,x)∈[0,T]×，随机微分方程(1)有唯一的强解,

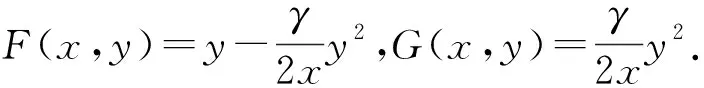
上述最优化问题是时间不一致的，按照Bjork和Murgoci[7]提出的方法，本文在博弈论框架下将原来的优化问题转化为寻找子博弈纳什均衡的问题.下面给出均衡控制策略和均衡值函数的定义.

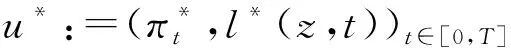
相应的均衡值函数V定义为V(t,x)=Ju*(t,x).

对于任意函数φ(t,x)∈C1,2([0,T]×)，定义无穷小算子

(2)

2 问题求解

由Bjork和Murgoci[7]的Theorem 4.1，给出下面的验证定理，其证明类似，故此处省略.

定理2.1 如果存在函数V(t,x),g(t,x)∈C1,2([0,T]×)以及f(t,x,y)∈c1,2([0,T]××) 满足下列条件，∀(t,x)∈[0,T]×和y∈,

(3)

并且

那么u*是均衡投资再保险策略，并且V(t,x)=Ju*(t,x)，即V(t,x)是均衡值函数.

注上述定理的条件，隐含函数f和g有下面的概率解释

(4)

(5)

定理2.2 定义2.1中均衡控制问题的均衡策略为

其中

并且

(6)

(7)

(8)

(9)

(10)

(11)

(12)

(13)

证明猜测HJB方程系统(3)具有如下形式的解

其中c1(t),c2(t),k1(t) 和k2(t)是确定的函数，在这种情形下，财富过程变为

构造如下的过程ρt:

则有

(14)

根据(14)式，可得

(15)

注意到

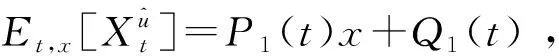
(16)

注意到V(t,x)=f(t,x,x)+(G◇g)(t,x)，所以HJB方程可以重写为

即

(17)

根据(4),(5)式可得

(18)

g(t,x)=P1(t)x+Q1(t).

(19)

假设(17)式等号左边的表达式在控制区间内取到最大值，分别对(17)式中的π和l求一阶偏导，令导数等于0，得

下面考虑值函数，因为有πt≥0,0≤l(z,t)≤z的限制条件，所以需要考虑下面的3种情况：

定理2.3 以上3种情况下定义2.1中控制问题的均衡值函数分别为：

情况1.V(t,x)的表达式为

(20)

其中P1(t),Q1(t),K(t),P2(t)和Q2(t)分别由(10),(11),(12),(13)和(16)式给出.

情况2.V(t,x)的表达式为在(20)式中取c2(t)=0,k2(t)=z.

情况3.V(t,x)的表达式为

(21)

因此有

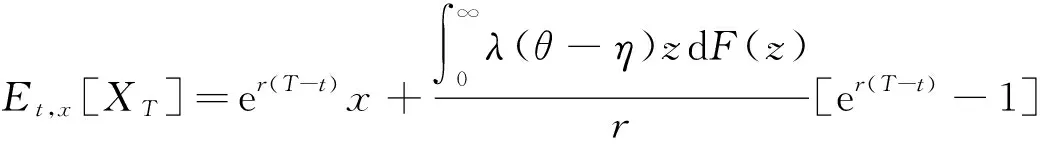
3 数值分析

这一部分给出数值实例来说明模型参数对均衡投资策略π*(t)的影响.假设初始盈余x=0.6，索赔大小服从参数为λz的指数分布，即分布函数为F(z)=1-e-λzz,z≥0.选择的模型参数值在表 1 中给出.

表1 保险市场和金融市场的参数

图1 γ,σ对π*(t)的影响

从图1，可以看到均衡投资策略π*(t)的动态变化.(a)图给出了风险厌恶系数γ对均衡投资策略π*(t)的影响，首先，对于一个给定的风险厌恶系数γ，π*(t)随着t的增加而增加，这意味着随着t的增加，保险人应该在风险资产中投资越来越多的钱，这一点和现实情况相一致；其次，对于固定的时间t，π*(t)随着γ的增加而减小，这一点也是合理的，一个较大的γ值意味着保险人有着更高程度的风险厌恶，风险厌恶水平高的保险人会选择在风险资产中会投资较少的资金.(b)图给出了风险资产的波动系数σ对均衡投资策略π*(t)的影响，π*(t)随着σ的增加而减小.σ较大意味着风险资产的收益会有更大的波动，因此，在相同的风险厌恶下，保险人会减少在风险资产中的投资金额.