变系数线性微分方程理论在年龄结构种群模型平衡态求解中的应用*

李盈科,张真真,张 瑜,李双喜,李岩松

(①新疆农业大学数理学院,830052,新疆维吾尔自治区乌鲁木齐市;②西北师范大学计算机科学与工程学院,730000,甘肃省兰州市)

0 引 言

微分方程模型是表达自然规律的一种自然的数学语言,是人们认识宇宙间事物运行规律的一种载体.一般情况下,这种运行规律的某些特性可以描述为一个微分方程组的柯西问题,这个柯西问题的解的适定性,特别是其中的解的存在唯一性,平衡点(态)的存在性以及其稳定性问题往往是研究的一个重要方面[1,2].Hisashi Inaba 在文献[2] 中介绍了如下婚姻模型,其中x(t,a),y(t,a) 和p(t,a)分别表示单身女性、单身男性以及成对夫妇在t时刻、a年龄的年龄依赖的密度函数.假设单身男、女的死亡率均为μ(a).夫妇的离婚率为σ(a), 结婚率为β(a).结婚函数为ρ(t,a)=Ψ(x(t,·),y(t,·))(a),尽管 Ψ(x,y) 并非关于x,y的线性函数,一般情况下采取平均意义的结婚函数ρ(t,a)=Ψ(1,1)(a)x(t,a).模型具体形式以如下偏微分方程组给出

(1)

模型(1)的平衡态E*=(x*(a),y*(a),p*(a)) 满足以下的初值问题

(2)

此处ρ(a)=Ψ(1,1)(a)x(a).以下为了简洁,平衡态E*的坐标仍以(x(a),y(a),p(a)) 给出.求模型(1)的平衡态转化为求柯西问题(2) 的解,本质上为求解一个变系数的线性常微分方程组的柯西问题.

许多经典教材对于求解一般的常系数线性常微分方程组的柯西问题都讲得很透彻,但对变系数的线性常微分方程组的柯西问题求解,尽管解的存在性理论已经很完备,但由于实际问题的多样性,求解析解并非易事,也没有统一方法,一般教材或文献也少有介绍[3].对问题(2),由基本理论[3],其理论解存在唯一.此外,本文应用蔡介福等在文献[4]中介绍的方法,以及应用特殊转化的方法来求模型 (2) 的解,展示了求解方法的多样性.首先,给出一些预备知识.

1 预备知识

(3)

或者写成

(4)

相对于系数矩阵A(x),构造以下超越函数方阵

EL(A)=A0(x)+A1(x)+A2(x)+…+An(x)+…,

(5)

其中A0(x)=I(n阶单位方阵),

以及

(6)

引理1[4]函数方阵无穷级数(5)和(6)式收敛、逐项可导,而且分别满足方程

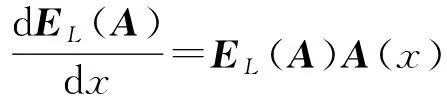
引理3[4]方程组 (3) 的通解为

注1 借助于EL(A) 与ER(A) 求解方程组(3),它的初值问题的解存在唯一,而且通解的结构不变.

2 求解方程组

解法1 利用文献[4]提出的解法,我们给出问题(2)的一般解法.为此,在方程组(2)中,记系数矩阵为

(7)

其中

a11(a)=Ψ(1,1)(a)+μ(a),a13(a)=-[σ(a)+μ(a)],

a21(a)=Ψ(1,1)(a),a22(a)=μ(a),a23(a)=-[σ(a)+μ(a)],

a31(a)=-Ψ(1,1)(a),a33(a)=σ(a)+2μ(a).

由(5)式,

其中

以此类推,

那么,按照(5)式,

EL(A)=A0(a)+A1(a)+A2(a)+…+An(a)+…=

I+A1(a)+A2(a)+…+An(a)+…=

(8)

其中

③ 石毓智,李讷.汉语语法化的历程——形态句法发展的动因和机制[M].北京大学出版社，2001.第2-3页.

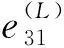
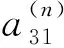
令

由引理3,设Y(a)=ER(-A)C是(2)中齐次方程组的通解. 由文献[4]定理三,

EL(A)|a=0=ER(-A)|a=0=I,

那么Y(0)=Y(a)|a=0=ER(-A)|a=0C=IC,从而得到C=Y(0).因此,(2)式的解为

Y(a)=ER(-A)Y(0).

(9)

注2 借助于文献[4]中给出的理论求出了变系数线性方程组 (2) 的形式解.

解法2 下面给出另外一种解法.假设方程 (2) 的平衡点E*(x(a),y(a),p(a)) 中x(a) 已知,由ρ(a)=Ψ(1,1)(a)x(a) 及(2)中第3个方程得

再由初始条件p0(0)=0以及一阶线性微分方程的常数变易公式可得

(10)

将其带入方程组(2) 中的第1个方程得

(11)

将 (10)式代入 (11)式整理得

(12)

这里

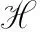
(13)

因此,由(12),(13)和(10),方程(2)的平衡点E*(x(a),y(a),p(a)) 存在.

注3 无论是变系数线性,还是常系数的线性常微分方程组的解,经典的方法是通过求基本解组而得到通解.对于常系数的线性常微分方程组,基本解组容易得到,但对于变系数线性线性常微分方程组来说,求解基本解组,至今尚无统一方法.利用积分方程理论和线性常微分方程组的常数变易法,给出了(2) 的形式解析解.

3 结论与数值模拟

利用文献[4]中给出的求解变系数线性常微分方程的方法,求解了一类年龄结构偏微分方程组的平衡态.同时,文中也给出了其他解法.下面给出一组数值模拟,在 (2) (或 (7) )中选取随年龄a变化的函数死亡率μ(a),离婚率σ(a)和结婚率Ψ(1,1)(a) 为以下形式

它们的函数图像见图 1，解的图像见图2.

图1 死亡率μ(a),离婚率σ(a)和结婚率Ψ(1,1)(a)随年龄a变化的函数图像