小学数学教学中渗透建模思想的策略
2021-08-26江苏省兴化市安丰中心小学
江苏省兴化市安丰中心小学 仇 华
数学学科中涉及的模型主要是指事物间的联系的总结或是相似的结构,数学中大部分公式、性质等都是来自现实生活。因此,在数学学习中,要想形成建模的思想,必须要学会联系生活,找到问题的连接点,只有这样才能更高效地解决问题。在数学探究过程中,善于借助建模思想有助于表达数学见解,更有助于解决生活中遇到的问题。对此,在实际的教学过程中,教师要重视对学生建模思想的培养和训练,让学生逐步形成一定的建模思想,进而更高效地解决问题。
一、创设学习情境,激活建模思维
在为学生设计相关的情境时,教师要先了解学生的实际情况,或是要对当前的时事热点做一定的了解,进而选择合适的主题,设计能够提升学生参与积极性的情境,让学生愿意主动投入学习中。一般来说,学生都具有一定的生活经历,在解决问题时,学生很容易联想到自己的经历,并进行一定的尝试,在这个过程中,学生就已经开始具备一定的建模思想。
例如,在对“探究平均数”一课进行教学时,教师向学生提出这样一个问题:已知A、B两组在进行算术比赛,两组都有五名成员,题目一共为十题,具体规则为对的一方积一分。A组最终得分为10分、7分、9分、8分、9分,B组最终得分为9分、8分、10分、6分、7分,请问哪一组赢了比赛?学生在听到问题后经过计算和比较,很快就有了结果。随后,教师又添加了一个条件:把A组成员改为6名 ,最终得分为10分、7分、9分、8分、9分、8分,问题不变。对此,学生都认为两组成员人数不一样,不能放在一起进行比较。这时,教师可以引导学生考虑在这种情况下,应该怎么样比较。会有学生认为可以比较两队的平均成绩,当学生回答出这一答案时,课堂的主要任务也就由此被引出,这就在一定的情境中让学生明白了“平均数”这一概念,这一过程也是学生自主参与数学建模的一个过程。
二、基于知识关联,引发建模猜想
在小学数学中,有很多知识点是相通的,所以在实际教学过程中,教师应当引导学生学会知识迁移,灵活运用。教师要抓住相关知识点的相通点,并在此基础上引导学生建立新的数学概念,即完成建模。在整个建模过程中,学生的思维将得到开拓,知识储备也将更丰富。
例如,在对“异分母分数的加减法”进行教学时,教师先提出这样一个问题:8.9元+9角=?
师:这可以直接计算吗?
生1:不行,加号前后数据的单位不一样,必须要转换后才可以。
师:对的,像这样前后单位不一样的情况,是不能够直接进行加减的,一定要先转换单位。我们今天就要来探究一下如何进行异分母的加减法,首先从这道题入手,大家看一下第一步怎么做?
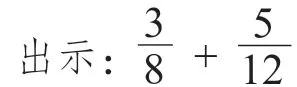
生2:先转换成同样的分母。
师:具体如何进行转换?
生3:分子分母同时加4后,分母就相同了,就可以直接计算了。
生4:这个做法是错误的。分子分母只有在同时乘或除以一样的并且不是零的数时才会保持和原分数一样,因此要将分母转化为8与12的最小公倍数后才可以计算。
师:哪一个做法是正确的呢?下面一起来探究一下。(适时导入课题)
在这个例子中,教师先从学过的“统一计量单位”入手,进而引导学生探究异分母分数的加减法,在此过程中联系了学过的知识,做到了知识迁移,完成了对新知识的建模。不仅知识范围,思维能力也得到了一定的拓展。
三、借助有效手段,培养建模方法
学生要形成建模思想需要一个长期培养和练习的过程。在整个过程中,教师要善于提升学生的积极性,带领学生逐步探究问题,并学会在解决问题的过程中联系生活实际,将问题转化成相关的数学模型。此外,教师应当向学生传输建模的思想,让学生感受到建模的好处,进而逐步形成建模的意识。通过建模,学会迁移知识,融会贯通。
1.在事理中建模
在学生解决实际问题的过程中,学生一定要善于结合自身的生活经验,丰富的生活经验十分有助于探索知识、解决问题,而且生活经验还能为学生进行建模提供启发。在探究过程中,当学生能够开始联系生活进行问题思考时,学生也就开始具备了一定的建模思想。比如,在探究“减法的性质”——“a-b-c=a-(b+c)”时,教师可以这样进行引导:如果把两块饼干一块一块地吃,这等同于什么?学生由此会想到“等同于一起吃完这两块饼干”。类似这种用生活经验来解释“数学概念”的方式,更有助于学生理解,进而完成数学建模。
2.在迁移中建模
美国教育心理学家奥苏伯尔认为:“有学习的地方就会产生迁移。”可见,学会迁移在学生形成建模思想的过程中所发挥的重要作用。在实际教学过程中,教师应当引导学生要多运用所学的知识以及自身的生活经验,通过不断比较和迁移完成建模。例如,教师在对“分数的基本性质”一课进行教学时,先为学生讲解了分数与除法间的联系,进而引导学生总结出“分数的基本性质”,完成对这一概念的数学建模。在知识迁移中完成新概念的建模,更有助于学生提升思维能力。
在教学时,教师一定要教会学生善于运用已经掌握的知识、经验等,为后续的建模做好充分的准备。具体的建模方法有很多种,除了上面提到的方法之外,还有图像法、比较法等。在学生成功建模前,教师一定要及时给予引导和帮助,让学生逐步养成意识,能够主动地进行数学建模,不断完善自身的数学学习方法。
四、引导自主探究,经历建模过程
传统的数学教学方式,一直都是脑力记忆,对于学生其他方面的能力并没有过多的考查,这种学习方式可以总结为“离身认知”,也就是与身体无关,单凭感觉的认知。而根据当前的认知理论不难发现,只有做到“具身认知”,也就是多方面调动感官参与认知,学习的效率才会得到极大的提升。这种方式的感知,对于学生的观察能力、思维能力等多方面都有一定的要求,最关键的一点就是要学生自己动手参与。而在数学学习中,自己动手参与是一件极为重要的事,单凭感受是达不到最佳效果的,只有做到“做数学”,学习才会更有效率,知识记忆才会更加深刻。
例如,在对“认识厘米”一课进行教学时,教师先根据逻辑顺序,让学生借助一定的工具来进行长度测量。由于学生的标准各不相同,所以教师就可以引导学生寻求统一的测量标准。然后,教师就可以向学生展示一个长度为一厘米的物体,让学生通过肉眼观察,在脑海里初步对“1厘米”的长度形成一定的印象。接着,再让学生把两根手指放在1厘米长的小棒的两侧,再挪开小棒,并保持手指的位置不变,那么手指间的距离即为1厘米。在学生感受过后,再将两只手指在保持距离的基础上不断开合,多次以后,学生对于“1厘米”的认知也会更加清晰。随后,教师又让学生闭上眼睛对1厘米的长度展开想象,并让学生回忆哪些物体长度在1厘米左右。在完成这些步骤后,学生再拿1厘米长度的小棒去测量物体就会感受更加深刻。此外,有一部分学生认为如果能够将多个长度为“1厘米”的小棒连起来,就能够形成一个“厘米尺”。在此基础上,教师再让学生用厘米尺进行测量时,又会出现两种方法:第一种是从零开始测量,第二种就是从任意一个数据开始。在对这两种方法的探讨中,学生逐步形成了“厘米尺能够测量长度”的认知。在整个探究过程中,学生调动了多方面的感官,不仅掌握了“厘米”这个概念,自主设计了“厘米尺”,还学会了借助“厘米尺”测量长度。通过上述教学方式,学生在探究的过程中做到了“具身认知”,各方面的感知都得到了训练。这样一来,学到的知识也会更加深刻。
总而言之,在小学数学的教学过程中,让学生逐步形成一定的建模思想尤为关键。数学建模不仅有助于学生追溯知识的源头,掌握本质,还有助于活跃和拓展学生自身的思维,不断提高学习效率。而对于教师来说,引导学生养成建模的习惯极为重要,教师要多借助相关的情境或是导学问题等手段,逐步带领学生形成建模的意识,提高学生的数学素养。
