基于HLLC格式的异重流高分辨率立面二维数学模型
2021-08-25卢新华秦超张小峰
卢新华 秦超 张小峰

摘要:异重流是自然界中的常见现象,异重流运动过程中交界面附近可能存在物理量的间断。为较好地捕捉这种间断,建立了异重流高分辨率立面二维数学模型,该模型基于同位网格的Godunov型有限体积法求解σ坐标下的雷诺时均Navier-Stokes方程组。模型中水平方向界面数值通量采用HLLC近似黎曼求解器计算,湍流封闭采用非线性K-ε模型。选用3个经典的开闸式平坡和反坡异重流试验对模型性能进行了检验。结果表明:该模型能较好地模拟异重流在平整或非平整床面上的运动过程,并具有较高的模拟精度。
关 键 词:
异重流; HLLC; 反坡异重流; σ坐标; 非线性K-ε模型
中图法分类号: TV131.2
文献标志码: A
DOI:10.16232/j.cnki.1001-4179.2021.06.021
异重流一般由两种或多种流体因较小的密度差而引起。自然界中常出现因盐度、温度、泥沙浓度差异而引起的盐水异重流、温差异重流和泥沙异重流等。在异重流运动的数值模拟研究中常涉及物理量的间断问题,较典型的如开闸式异重流,其在流体交界面附近存在较大梯度,数学模型若不在间断处进行特殊处理较易产生数值震荡[1-2]。目前,常用的异重流数学模型主要包括单层或深度平均数学模型,以及三维或立面二维数学模型[3-6]。对于单层或深度平均异重流数学模型而言,不同学者处理间断方式不同,如Klemp等[7]及Ungarish等[8]在计算中采用显式追踪间断位置,另有研究则采用激波捕捉数值格式以自动捕捉数值间断[9-12];这类模型在间断处通常须引入一系列假定(如假定间断处局部弗氏数为某一经验取值[2,7]),且模型中尚须引入卷吸系数、层间阻力系数以反映流体层间的质量交换和动量交换[9-10],同时,模型无法描述流体界面附近的物理掺混过程。相比单层深度或平均异重流数学模型,三维模型可自动反映流体层间的质量和动量交换,能描述交界面附近异重流的掺混过程,因而在理论上比前者能更好地描述异重流的运动,但三维数学模型依然要处理界面间断問题。近30 a来,近似黎曼求解器被广泛应用于计算界面间断问题,如溃坝洪水波、近岸海域波浪破碎、空气动力学中激波问题的模拟研究[13-16],并取得了较大成功。然而在异重流三维(立面)二维数值模拟方面鲜有研究报道。本研究尝试基于文献[14]提出的HLLC近似黎曼求解器建立模拟异重流运动的立面二维数学模型,以期检验近似黎曼求解器在异重流运动模拟方面的性能。模型中垂向采用σ坐标变换。
1 数学模型
采用Boussinesq近似、忽略非静压和垂向加速度影响,并引入垂向σ坐标变换(以适应不规则床面地形和捕捉水面变化)
t′=t,x′=x,σ=z′=z-zbh(1)
式中:t为时间;x,z为笛卡尔直角坐标;zb,h分别为河床高程及水深。可得σ坐标下雷诺时间平均的立面二维异重流运动控制方程组:
ht′+qxx′+ωσ=0(2)
qxt′+uqx+12gh2x′+uωσ=-ghzbx′
-ghx1ρ∫ηzρ-ρ0dz+S′ν,u(3)
qct′+uqcx′+cωσ=S′ν,c(4)
式中:ω=hdσdt=hσt+uσx+wσz;u,w分别为x,z 2个方向的流速分量;c为溶质(体积)浓度;qx=hu,qc=hc;g为重力加速度;ρ=1-cρ0+cρc,这里ρ0,ρc,ρ分别为水、溶质及混合密度;S′ν,φ为扩散项,并用下式计算:
S′ν,φ=x′ν+νtoφhφx′+σν+νtoφ1h2qφσ(5)
式中:φ=u,c;ν与νt分别为分子与湍流运动黏性系数,本文研究中νt采用经浮力修正的非线性K-ε两方程湍流模型计算:
qKt′+uqKx′+Kωσ=S′ν,K+hGs+Gb-ε(6)
qεt′+uqεx′+εωσ=S′ν,ε+
hεKC1εGs+C3εGb-C2εε(7)
式(5)~(7)中:νt=CμK2ε;qK=hK,qε=hε;S′ν,K和S′ν,ε采用式(5)计算(式(5)中φ=K,ε);Gb=1hgρνtocρσ为浮力产生项;Gs=-u′iu′juixj为剪切力产生项,在非线性K-ε模型中,
u′iu′j=23Kδij-CdK2εuixj+ujxi
-C1×K3ε2uixlulxj+ujxlulxi-23ulxkukxlδij
-C2×K3ε2uixkujxk-13ulxkulxk
-C3×K3ε2ukxiukxj-13ulxkulxkδij(8)
式中经验参数取值为:Cμ=0.09,C1ε=1.44,C2ε=1.92,ou=oν=oc=oK=1.0,oε=1.3,Cd=2317.4+Smax,C1=1185.2+D2max,C2=158.5+D2max,C3=1370.4+D2max,Smax=Kmaxuixi, Dmax=Kmaxuixj(Smax与Dmax计算中不采用Einstein求和约定);式(8)中i,j,k,l=1,2。参考文献[17,18],C3ε取值为0。
2 数值离散
本文基于同位网格的Godunov型有限体积法进行数值求解。为方便数值离散,将式(1)~(7)写成如下守恒型矢量形式:
Ut′+Fx′=-Hσ+S0+Sν,H+Sν,σ+Sρ+Se(9)
其中,
U=hqxqcqKqε,F=qxuqx+g2h2uqcuqKuqε,H=ωuωcωKωεω(10)
S0=0-ghzbx′000
Sν,H≈0x′ν+νtouhux′x′ν+νtochcx′00
Sν,σ≈0σν+νtou1h2quσσν+νtoc1h2qcσ00(11)
Sρ=0-ghx1ρ∫ηzρ-ρ0dz000
Se≈000hGs+Gb-εhεKC1εGs+C3εGb-C2εε(12)
式(9)中Sν,H,Sν,σ为σ坐标下水平与垂向黏性扩散项矢量。
对式(9)采用两步二阶Runge-Kutta方法进行时间步进离散:
UIi,k=UNi,k+UI-1i,k2+αIΔt2Ri,k(13)
式中:i,k为网格单元编号;N为时间层;Δt为时间步长;I为Runge-Kutta步数。α(1)=2,α(2)=1。
Ri,k=FI-1i-1/2,k-FI-1i+1/2,kΔx′i+HI-1i,k-1/2-HI-1i,k+1/2Δσk+
Sl0+Slν,H+Slν,σ+Slρ+Slei,k(14)
Δx′=x′i+1/2-x′i-1/2,Δσk=Δσk+1/2-Δσk-1/2;当I取1和2时,UI-1i,k分别取UNi,k和U1i,k;式(14)中当l取(I-1)或I时,表示该项显式或隐式离散,本文模型除Sν,σ隐式离散外Ri,k中其他部分均显式离散。
式(14)中水平方向界面数值通量Fi±1/2,k采用HLLC近似黎曼求解器计算如下[13-14]:
Fi-1/2,k=FLi-1/2,k 0≤ξLi-1/2,kF*Li-1/2,k ξLi-1/2,k≤0≤ξMi-1/2,kF*Ri-1/2,k ξMi-1/2,k≤0≤ξRi-1/2,kFRi-1/2,k ξRi-1/2,k≤0(15)
其中,
FL=FUL (16-1)
FR=FUR(16-2)
F*L=F*1F*2wLF*1KLF*1εLF*1T(16-3)
F*R=F*1F*2wRF*1KRF*1εRF*1T(16-4)
F*=F*1F*2F*3F*4F*5T=
ξRFL-ξLFR+ξLξRUR-ULξR-ξL(16-5)
式(15)中,波速ξL,ξR,ξM采用下式计算:
ξL=uR-2 ghRhL=0minuL- ghL,u*- gh*hL>0ξR=uL+2 ghLhR=0maxuR+ ghR,u*+ gh*hR>0ξM=ξLhRuR-ξR-ξRhLuL-ξLhRuR-ξR-hLuL-ξL(17)
u*=12uL+uR+ ghL- ghRh*=1g12 ghL+ ghR+14uL-uR2(18)
式(14)中垂向方向界面数值通量Hi,k±1/2采用加权二阶中心-一阶迎风格式计算,如
Hφi,k-1/2=wi,k-1/2θφC+1-θφUPi,k-1/2(19)
这里φ可取任意变量,如u,w,K,;θ为加权系数,取值越小模型越稳定、越大精度越高,本文取1.0以提高模拟精度;φCi,k-1/2=Δσk-1Δσk-1+Δσkφi,k+ΔσkΔσk-1+Δσkφi,k-1,φUPi,k-1/2=12φi,k-1+φi,k+12signwi,k-1/2φi,k-1-φi,k。
计算中床面阻力项采用全隐式离散,式(12)Sρ中水平方向偏导数在笛卡尔直角坐标系下进行计算,模型中通量项与源项的离散能严格保证静水平衡。模型中的水流模块计算原理及性能检验详见文献[13],本文异重流模型基于该水流模型扩展得到。
3 模型检验
本文采用3个经典的室内异重流试验以检验模型性能,其中包括平坡和反坡异重流试验。考虑到所选取的试验中异重流均沿水槽底部流动,为提高模型模拟精度,模拟中对床面附近网格进行加密处理,垂向网格结点的σ坐标值采用下式计算:
σk=β+1λk-β-1λkβ+1λk-1+β-1λk-1(20)
式中:λk=k-1∕nz,k=1,2,…,nz+1,为垂向网格结点编号,nz为垂向网格单元数;β为控制垂向网格疏密的因子(β>1)。当β越趋近于1时底部网格越密集,网格分布越不均匀;当β越大时网格分布越均匀。本文计算中β取值1.3。
3.1 Adduce等平坡异重流试验
Adduce等[9]在羅马大学的水力学实验室进行了一系列开闸式平坡异重流试验,试验水槽如图1所示,水槽两端封闭,长度为L、宽度为b、高度为H0。在距离水槽左端x0处有一闸门,闸门左侧为盐水、密度为ρ1,右侧为淡水、密度为ρ0,闸门两侧初始水深相同,均为h0。试验时,迅速开启的闸门,因流体密度差异,在重力作用下密度较大的流体会沿水槽底部运动而形成异重流。选取其中两组具有代表性的试验工况进行模拟,这两组工况分别命名为“工况1”和“工况2”。计算中,L=3 m,b=0.2 m,其余参数如表1所列。表1中,g′=ρ1-ρ0ρ1g为因密度差异造成的初始有效重力加速度,这里g=9.81 m/s2。
基于线性-对数律计算床面切应力。为保证计算精度并提高计算效率进行了网格无关解分析。研究中选取了nx×nz=100×5,200×10,300×20及300×30四套网格进行模拟,其中nx、nz分别为水平和垂向方向的网格单元数。图2(a)、2(b)分别为2组工况下计算的异重流头部位置随时间变化与实测值的比较。从图2可以看出,nx×nz=300×20与nx×nz=300×30两套网格计算结果接近,考虑到该算例计算量不大、本算例取nx×nz=300×30。图2表明,本文模拟结果与试验结果吻合较好。
图3为计算的典型工况(以工况1为例)不同时刻的浓度分布及流场。在异重流开始坍塌阶段(见图3(b)),左侧盐水下潜入侵右侧淡水形成一个大尺度的涡漩,同时在水面上形成一个微小振幅的波浪向右传播(图3(b)水槽中部流场为该波传播到此处引起)。此后,异重流沿水槽底部继续向前运动(见图3(c)),并逐步进入自相似阶段(见图3(d))。由图3可以看出,模型能较好地模拟异重流在平整床面上的运动过程。
3.2 Hatcher等平坡异重流试验
为进一步检验模型精度,本文选取Hatcher等[2]异重流试验数据对该模型进行验证。在长L=9.14 m、宽b=0.127 m的水槽中共进行了两个组次的试验,每个组次的试验均重复进行了3次以保证试验的可重复性,试验原理同2.1节,试验具体参数如表2所列。试验中采用MicroADV测量了x*=6.68所在断面的水槽中部垂线上距床面3个不同位置高度的异重流内部流速。监测点处的无量纲高度分别为h*A=hA/h0=0.188,0.125和0.063,hA为监测点到水槽底部的垂直距离。
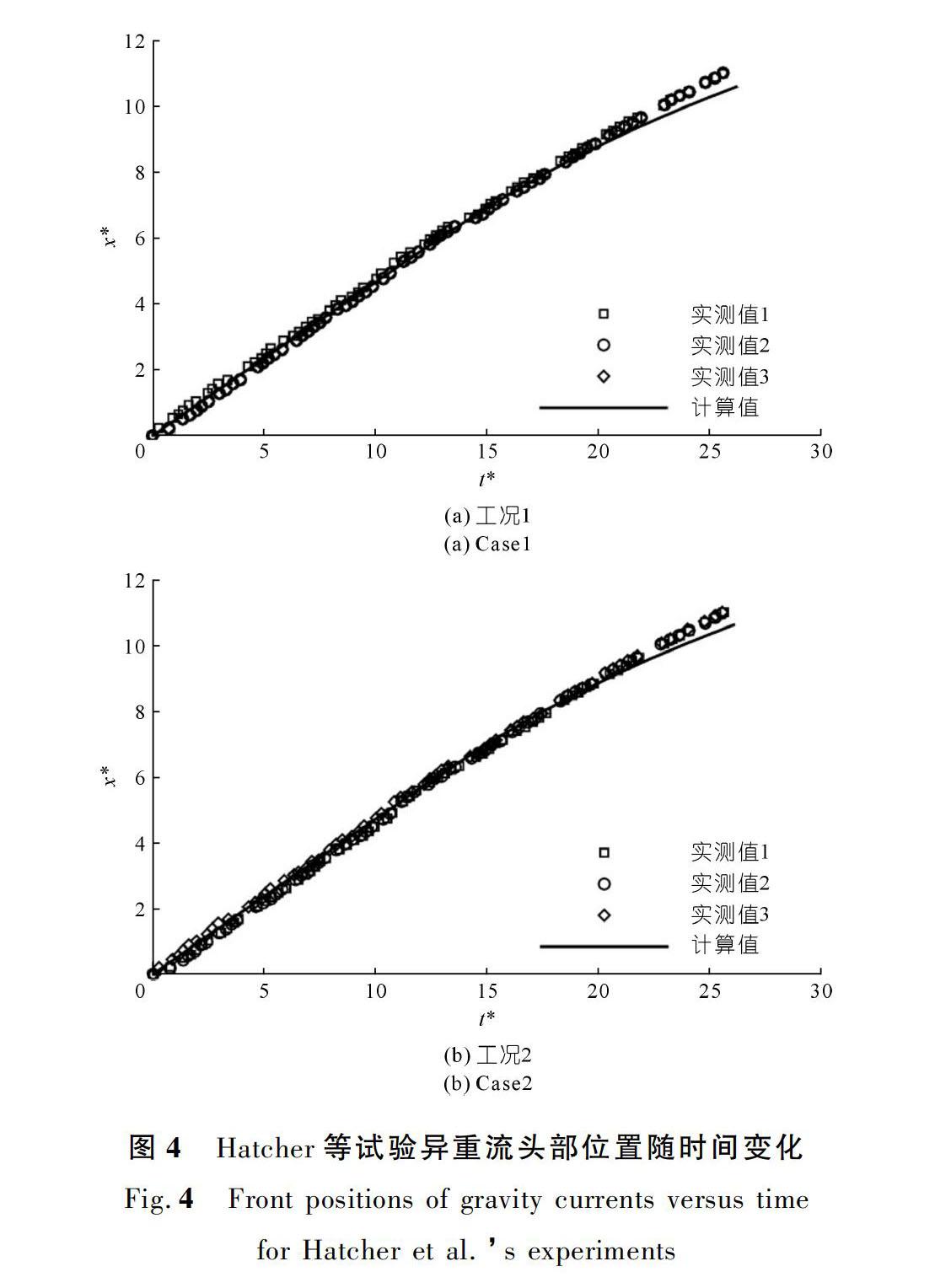
类似于3.1节算例,此节算例经网格无关解分析后选取nx×nz=1 800×30。图4(a)、4(b)分别计算了工况1和工况2下无量纲化异重流运动距离随时间变化与实测值的比较,其中“实测值1”“实测值2”“实测值3”为每组工况下重复的3次试验数据。图4中无量纲异重流头部位置定义为x*f=x/x0,其中x为异重流头部到闸门处的距离;无量纲时间定义为t*=t/x0 g′h0。由图4可知,模拟的异重流头部位置随时间变化的结果与试验数据吻合良好。
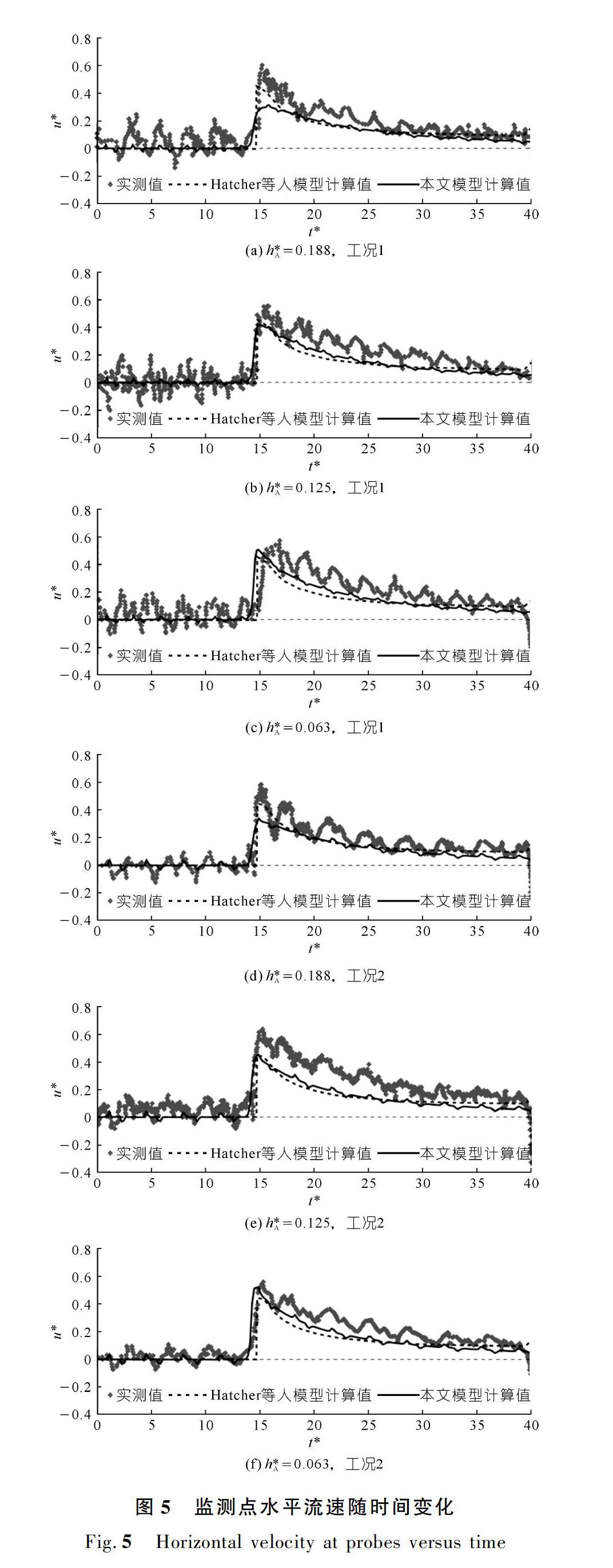
图5给出了2种工况下不同位置高度处监测点水平流速随时间变化的计算值与实测值的比较。图5同时给出了Hatcher等[2]采用双层深度平均模型的计算结果。由于该模型求解上层水体与下层异重流流速的垂线平均值,因此,图5中同一工况下各个垂线位置处该模型的流速计算值相同。由图5可看出,2种工况下,在异重流头部到达监测点之前(t*≤15),各监测点的流速值相对较小,而当异重流头部到达监测点时(t*≈15)流速值迅速增大,之后各监测点流速随时间有逐渐减小的趋势,本文模型和Hatcher等人的双层深度平均数学模型均能较好地反映异重流内流速的这一变化过程。由图5亦可知,相比双层深度平均数学模型,本文模型能模拟异重流流速在垂线上的分布,且与实测值较为吻合。
3.3 Marleau等反坡异重流试验
为检验模型在非平整床面上异重流的模拟性能,本节选取Marleau等[21]开闸式反坡异重流试验作为验证算例,试验水槽如图6所示,水槽长L1=1.975 m,宽b1=0.176 m,高H1=0.485 m。闸门与水槽左端的距离为Ll,水槽右端插入一块刚性塑料板作为底坡、其长度为Ls。试验时,闸门左侧水槽底部填充高度为D、密度为ρ1的盐水,周围淡水的密度为ρ0。本次模拟的试验参数为:D=H=0.3 m,ρ1=1 001 kg∕m3,ρ0=998.5 kg/m3,Ll=0.284 m,Ls=1.2 m,坡度s=0.25。经网格无关解分析后,计算中选取nx×nz=600×30的网格。
不同时刻的浓度分布及流场如图7所示,图中t从异重流到达斜坡底端时起算。当异重流到达斜坡底端时(见图7(a)),异重流厚度约为初始水深的一半,异重流与周围水体交界面处产生一大尺度的涡漩;之后,异重流在惯性作用下沿斜坡向上运动(见图7(b)),当异重流爬坡到某一高度时,异重流与清水交界面附近出现两个大尺度的涡漩(见图7(c)),该阶段在重力与床面阻力影响下异重流运动速度降低,头部厚度也逐渐减小。
图8为异重流运动距离随时间变化与实测值的比较,其中x′为异重流沿斜坡向上运动的距离。由图8可知,异重流沿斜坡向上做减速运动,总体上数值模拟结果与试验数据吻合良好。
4 结 论
本文基于HLLC近似黎曼求解器建立了异重流高分辨率立面二维数学模型,该模型采用σ坐标变换以适应不规则床面地形和捕捉水面变化。文中选用3个涉及到物理量间断的开闸式平坡及反坡异重流试验对模型性能进行检验,检验结果表明模型能较好地捕捉间断问题,并在异重流模拟方面具有较高精度。
需要说明的是,本文建立的模型为立面二维数学模型,但较易拓展成三维数学模型以模拟复杂边界条件下异重流的三维运动过程。另外,本文模型中湍流模型采用的是非线性K-ε两方程模型、水平方向数值通量采用HLLC近似黎曼求解器,今后可对比研究其它湍流模型及近似黎曼求解器在异重流模拟方面的模拟性能。
参考文献:
[1] ROTTMAN J W,SIMPSON J E.Gravity currents produced by instantaneous releases of a heavy fluid in a rectangular channel [J].Journal of Fluid Mechanics,1983(135):95-110.
[2] HATCHER T M,VASCONCELOS J G.Finite-volume and shock-capturing shallow water equation model to simulate Boussinesq-type lock-exchange flows [J].Journal of Hydraulic Engineering,ASCE,2013,139(12):1223-1233.
[3] 方春明,韓其为,何明民.异重流潜入条件分析及立面二维数值模拟 [J].泥沙研究,1997(4):70-77.
[4] 彭杨,李义天,槐文信.异重流潜入运动的剖面二维数值模拟 [J].泥沙研究,2000(6):25-30.
[5] 张芝永,杨元平,程文龙.异重流三维非静压数值模拟研究 [J].中国水运,2018,18(11):74-76.
[6] 陆俊卿,张小峰,崔占峰.各向异性密度流模型及其验证 [J].水科学进展,2010,21(1):95-100.
[7] KLEMP J B,ROTUNNO R,SKAMAROCK W C.On the dynamics of gravity currents in a channel [J].Journal of Fluid Mechanics,1994(269):169-198.
[8] UNGARISH M,ZEMACH T.On the slumping of high Reynolds number gravity currents in two-dimensional and axisymmetric configurations [J].European Journal of Mechanics-B/Fluids,2005,24(1):71-90.
[9] ADDUCE C,SCIORTINO G,PROIETTI S.Gravity currents produced by lock exchanges:experiments and simulations with a two-layer shallow-water model with entrainment [J].Journal of Hydraulic Engineering,ASCE,2012,138(2):111-121.
[10] HU P,CAO Z X,PENDER G,et al.Numerical modelling of turbidity currents in the Xiaolangdi reservoir,Yellow River,China [J].Journal of Hydrology,2012(464-465):41-53.
[11] LU X H,DONG B J,MAO B,et al.A robust and well-balanced numerical model for solving the two-layer shallow water equations over uneven topography [J].Comptes Rendus Mécanique,2015,343(7-8):429-442.
[12] LIN J,MAO B,LU X H.A two-layer hydrostatic-reconstruction method for high-resolution solving of the two-layer shallow-water equations over uneven bed topography [J].Mathematical Problems in Engineering,2019(2019):1-14.
[13] LU X H,MAO B,ZHANG X F,et al.Well-balanced and shock-capturing solving of 3D shallow-water equations involving rapid wetting and drying with a local 2D transition approach [J].Computer Methods in Applied Mechanics and Engineering,2020(364):112897.
[14] TORO E F.Riemann solvers and numerical methods for fluid dynamics [M].Newjersey:Springer,2009.
[15] CAO Z X,PENDER G,WALLIS S,et al.Computational dam-break hydraulics over erodible sediment bed [J].Journal of Hydraulic Engineering,ASCE,2004,130(7):689-703.
[16] LU X H,XIE S B.Depth-averaged non-hydrostatic numerical modeling of nearshore wave propagations based on the FORCE scheme[J].Coastal Engineering,2016(114):208-219.
[17] MA G F,KIRBY J T,SHI F Y.Numerical simulation of tsunami waves generated by deformable submarine landslides [J].Ocean Modelling,2013(69):146-165.
[18] 盧新华.基于近似黎曼求解器的三维浅水方程组求解方法 [J].人民长江,2018,49(20):74-80.
[19] CHOWDHURY M R,TESTIK F Y.Laboratory testing of mathematical models for high-concentration fluid mud turbidity currents [J].Ocean Engineering,2011,38(1):256-270.
[20] HUPPERT H E,SIMPSON J E.The slumping of gravity currents [J].Journal of Fluid Mechanics,1980,99(4):785-799.
[21] MARLEAU L J,FLYNN M R,SUTHERLAND B R.Gravity currents propagating up a slope [J].Physics of Fluids,2014,26(4):213-234.
(编辑:李 慧)
A vertical 2D high-resolution numerical model for gravity current based on HLLC scheme
LU Xinhua,QIN Chao,ZHANG Xiaofeng
(State Key Laboratory of Water Resources and Hydropower Engineering Science,Wuhan University,Wuhan 430072,China)
Abstract:
Gravity currents are common phenomenon in nature.Discontinuities may exist near the interface during the movement of gravity currents.In order to capture this discontinuity well,we develop a vertical 2D high-resolution numerical model for gravity currents.The developed model uses the Godunov-type finite-volume method based on the isometric grid to solve the Reynolds time-mean Navier Stokes equations in σ coordinates.The horizontal inter-cell numerical flux is evaluated by the HLLC approximate Riemann solver,and the MUSCL scheme is employed for horizontal interface value reconstructions.A nonlinear k-ε model is employed for turbulence closure.Three classic lock-exchange experiments of gravity currents propagating on flat and adverseslope beds are employed to verify the performance of the model.Results show that the developed model simulates the movement of gravity currents well on flat or uneven bed with high accuracy.
Key words:
gravity current;HLLC;gravity current on adverse slope;σ coordinates;nonlinear k-ε model
