降雨条件下弃渣场边坡暂态饱和区分布及稳定性

张晋梅 张震 李家春

摘要：为了研究弃渣场边坡在降雨条件下的失稳机理，以贵州省道真县至瓮安市高速公路路边某弃渣场边坡为研究对象，利用GEO-Studio中的SEEP/W模块，在室内试验基础上研究了弃渣场边坡在降雨条件下暂态饱和区的分布规律，并利用SLOPE/W模块研究了暂态饱和区分布与边坡稳定性之间的联系。结果表明：① 降雨对弃渣场边坡稳定性的影响在降雨停止之后依旧会持续很长一段时间，这段时间安全系数会持续降低并最终达到最小值。② 坡面暂态饱和区从开始形成到坡面坡顶全部饱和只需要很短的一段时间，这段时间也是边坡安全系数下降速度最快的时间段;坡面暂态饱和区形成以后，降雨对边坡稳定性的影响显著降低。

关 键 词：

弃渣场边坡; 暂态饱和区; 边坡稳定性; 非饱和土; 基质吸力

中图法分类号： U417.2

文献标志码： A

DOI：10.16232/j.cnki.1001-4179.2021.06.026

隧道开挖等工程会产出大量的弃渣，其主要由松散土、碎石等组成。大孔隙、非饱和是弃渣的主要特点，其具有残积层的渗透性质，同时由于其压实度不够，导致其强度较低，容易发生滑坡泥石流等灾害。最为大众所熟知的弃渣场滑坡灾害就是发生在2015年12月的深圳光明新区弃渣场滑坡灾害，滑坡共造成4人死亡，76人失联。弃渣场滑坡的危害程度之大在学术界已经形成共识，迄今为止已有不少学者对此开展了研究。吴谦等[1]对某弃渣场进行了研究，分析了边坡稳定系数对参数的敏感性，并借助Monte Carlo算法对其稳定性可靠度进行了研究。李叶鑫[2]采用主成分分析方法，分析了不同堆积时间下的弃渣场入渗特征。吴伟东等[3]建立基于（PPC）模型的风险评价体系，结合贵昆线铁路10座弃渣场研究发现弃渣场边坡条件和地形与地基条件两个维度对弃渣场的综合风险影响最大。孙朝燚等[4]为了研究坡体走向对边坡稳定性的影响，针对某核电厂弃渣场，通过现场地质调查和区域划分研究了弃渣场边坡的走向夹角对其潜在破坏机制的影响。聂超等[5]结合前期勘察资料模拟研究了不同降雨条件下地下水位等值线分布状态，并对不同降雨条件下高填方边坡变形特征进行研究分析，得出不同降雨条件下的渗流场分布情况以及相对应的变形规律。高飞等[6]以某弃渣场设计为背景，通过创建三角网体积曲面探讨了AutoCAD Civil 3D在弃渣场水土保持工程设计中应用的主要优点，以及该软件在水土保持工程设计中的应用前景。

本文在前人研究的基础上对弃渣场边坡降雨条件下暂态饱和区发生发展规律進行了分析研究，并将其发展规律与弃渣场边坡安全系数的变化结合起来进行了综合分析。研究得到了该类型弃渣场边坡暂态饱和区发展规律以及与边坡稳定性之间的联系，可为弃渣场的选址、坡面排水设施的设计施工、边坡稳定性监测等工程提供参考。

1 数值分析理论

基于达西定律的二维有限元方程为[7]

ΚH+MH=Q（1）

式中：[K]为单元特征矩阵;{H}为节点水头向量;[M]为单元质量矩阵;{Q}为节点流量向量。

1980年Van Genuchten[8]基于大量试验提出了VG统计模型，如式（2）和式（3）所示。

θ=θr+θs-θr1+ψanm（2）

式中：θ为体积含水率;θs为饱和体积含水率;θr为残余体积含水率;ψ为基质吸力;a，m，n为拟合参数。

kr=1-ψan-11+ψan-m21+ψanm2（3）

式中：kr为相对渗透系数;由于忽略了孔隙气压的影响即ua=0，所以-p=u即为基质吸力;ψ为基质吸力;a，m，n为拟合参数。

本文采用VG模型拟合试验数据的方法得到渗流过程中基质吸力和体积含水率以及渗透系数的关系。同时采用极限平衡法对边坡的稳定性进行分析，利用静力力学平衡和土的Mohr-Coulomb破坏准则对土体稳定性进行分析判断，即通过分析极限状态下坡体的稳定性得到坡体的安全系数[9]。采用经典的Bishop法进行稳定性分析。

2 项目概况

本文研究点地貌类型为构造侵蚀溶蚀低中山地貌，坡度多在30°～50°，坡体上部坡度60°～80°，悬崖峭壁遍布并伴有崩塌堆积体（见图1）。坡面多堆积，坡脚一般有冲刷能力较强的溪流流过。岩性主要为二叠系灰岩及志留系泥岩及泥灰岩等，少量奥陶系的泥岩、页岩及灰岩。其中位于二叠系地层段的岩溶地貌发育，溶沟、溶槽较发育。主体山脉大致呈东西走向。整体地势西高东低，最高海拔高程807.5 m，最低海拔高程767.0 m，相对高差40.5 m。

弃渣体地层出露主要为扬子一级地层区，路线走廊带出露的地层有第四系、二叠系、志留系、奥陶系、寒武系等。岩性以灰岩、白云岩为主夹少量泥岩、页岩。弃渣体所处属亚热带季风湿润气候区，年平均气温16.2 ℃，年平均降水量1 071.8 mm。

综上所述，基岩为相对稳定的灰岩组成，且坡度较陡;同时，考虑到其降雨量充沛，应重点考虑降雨对其稳定性的影响，故而，在现场勘察的基础上切取图2所示弃渣体的剖面，建立二维数值分析模型。

3 计算参数与方案设计

为了对边坡孔隙水压力、暂态饱和区以及弃渣体稳定性进行分析，利用简单高效的地质工程通用仿真软件GEO-Studio中的SEEP/W模块建立如图2所示计算模型。SEEP/W模块是一款分析多孔透水材料中的地下水渗流以及孔隙水压力分布状态等问题的数值分析软件，对饱和非饱和问题中考虑历时的研究尤其出色。为了分析不同时刻不同深度孔隙水压力分布情况，取x=50 m处断面孔压进行分析。

模型边界条件：两侧按零流量边界处理，底边按不透水边界处理，地下水水头设置为零。而上边界由于降雨入渗的复杂性，需要将入渗分为2种情况[10]：① 降雨强度小于边坡入渗能力，此时降落到坡面的雨水全部渗入，按流量边界考虑，而当降雨强度大于边坡入渗能力时，坡面形成积水，此时应按压力边界处理。实际情况下单位流量大小随历时改变，为了控制降雨雨型等因素对暂态饱和区分布的影响，本文参考当地6月降雨数据，设置强度大小为0.052 m/h的均匀降雨边界，此数值大于弃渣饱和渗透系数0.022 m/h。降雨历时5 h，计算总时长12 d。

弃渣体土水特征曲线采用试验数据点进行拟合得到，具体方法是将压力板仪产生的吸力数据导入SEEP/W模块的材料定义界面中，并基于公式（2）、（3）提到的VG模型拟合得到。同理，渗透系数曲线采用VG模型在土水特征曲线的基础上拟合生成如图3所示曲线，横坐标为对数坐标;图4横纵坐标都为对数坐标。

在降雨过程中为了分析边坡稳定性与暂态饱和区之间的关系，需在暂态饱和区各个发展阶段对其稳定性进行计算分析。通过室内大型直剪试验确定材料力学参数如表1所列。考虑到挡土墙的整体性较好，且正常工作，所以在分析过程中赋予其较大的强度。

4 数据分析

4.1 弃渣场渗流分析

将降雨边界施加到模型表面后，计算得到x=50 m断面处体积含水率随时间的分布，如图5所示。降雨发生后，边坡表面体积含水率并不是线性增大，而是以增幅逐渐降低的方式增大。在3 h后坡面体积含水率维持在0.18不再变化，此时地表弃渣土体达到饱和状态。在5 h降雨停止后，到6 h坡面体积含水率依旧维持在0.18，表明随着降雨的停止，坡面体积含水率并不会立马开始下降。在y=16 m位置可以看到，由于土体性质的不同，在层面处体积含水率有一个较大的拐点。同时由于地下水的存在，使得在基岩部分y=18 m以下深度范围，深度越大含水率越高，且是以幅度逐渐增大的趋势增加。

当土体体积含水量达到饱和状态的0.9时，即可认为此时弃渣体达到饱和状态[11]。这对应于本文当弃渣体体积含水率达到0.16时，即可认为弃渣达到饱和状态。如图5虚线所示，在降雨停止约7 h（即计算12 h）坡面仍处于饱和状态。由此得出结论：坡面暂态饱和区并不会随着降雨的停止立刻开始消散。

图6为x=50 m处孔隙水压力随深度的变化。在坡顶浅层部分变化规律与体积含水率相似，在降雨3 h后坡面即达到饱和状态且孔压不再增加。直到5 h，孔压依旧维持不变，说明坡面积水深度不再增加，在积水达到一定深度即在坡面形成径流沿着坡面往坡底流动。此径流易对坡面产生冲刷，影响边坡的稳定，所以应在坡顶设置截水沟等排水设施避免坡面被冲刷发生失稳。

5 h降雨停止后，孔压开始逐渐下降，这是由于地表水的下渗所致。地表孔压在降雨停止163 h后（7 d）依旧未恢复到降雨前水平，说明降雨对边坡的影响是一个较漫长的过程。因此在对边坡进行安全监测的时候，工作重心不能仅仅放在降雨期间，还要适当延长。

同时还可以发现随着降雨的进行每个时间点的拐点也是在不断向右边偏移。这是因为深层土体逐渐受到降雨的影响，基质吸力开始逐渐消散，孔压开始变大。通过该现象可以判断出土体受降雨影响的深度，对应该弃渣场，降雨影响的深度约为20 m。

在坡顶弃渣填筑较浅部分，雨水很快入渗到层面位置，由于渗透系数的差异，雨水沿着层面往坡脚渗流。如果降雨时间延长到一定阈值，雨水会在层面位置汇集，降低层面位置土体强度并导致弃渣体沿着层面发生滑坡失稳。所以在对弃渣场进行选址时，在充分考虑基岩强度的同时，基岩透水性能指标也是一个值得考虑的因素。在该弃渣场已经填筑形成的情况下，应在挡土墙层面位置设置排水孔，疏导层间水流。

图7（a）中，降雨1 h，此时坡面未达到饱和状态，雨水全部入渗。图7（b），降雨2 h，坡面饱和度开始逐渐增大，坡脚饱和度相对增大得更快，并在坡顶位置形成径流（蓝色虚线）。图7（c），降雨3 h，坡面已经全部达到饱和状态。图7（d），降雨5 h，相对3 h时坡面暂态饱和区状态，除了雨水持续入渗，坡面暂态饱和区分布不再发生变化。图7（e），降雨停止20.5 h（即计算25.5 h后）坡顶暂态饱和区消散，紧接着26 h坡面暂态饱和区消散。

综合以上分析笔者认为：

① 降雨发生期间，影响该弃渣场暂态饱和区分布的只是前3 h。在暂态饱和区稳定形成以后，降雨对暂态饱和区分布的影响显著降低，此时因为坡面已经饱和并形成径流。

② 降雨期间，饱和区从坡脚逐渐发展到坡顶，而降雨停止之后暂态饱和区的消散是从坡顶往坡脚逐渐消散。

4.2 弃渣场边坡稳定性分析

弃渣场土体力学参数如表1所列，采用Bishop法对边坡稳定性进行分析。在本次计算中考虑了基质吸力对边坡抗剪强度τ的影响，如公式（5）所示[12]：

τ=c ′+σn-σatanφ′+ua-uwtanφb（5）

式中：τ为抗剪强度;c′有效凝聚力;φ′为有效內摩擦角;ua-uw为基质吸力，由于不考虑气压影响，所以-uw即为基质吸力;φb为基质吸力引起的内摩擦角，本文中φb的大小由土水特征曲线控制。

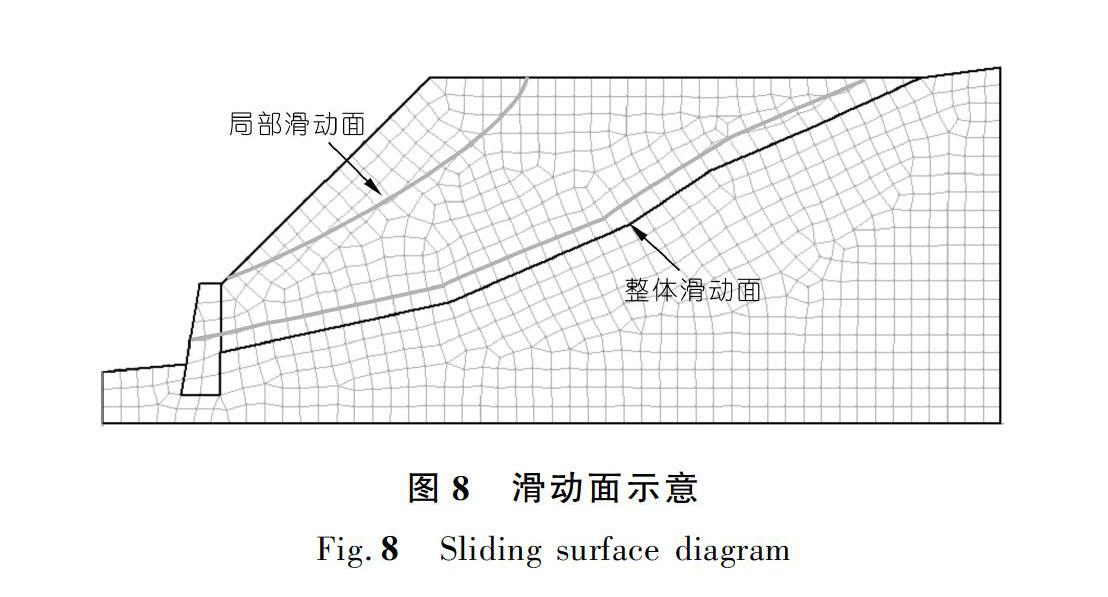
在对弃渣场稳定性进行分析的过程中，考虑到弃渣场基岩的稳定性很好，所以在进行弃渣场稳定性分析的过程中将基岩设置为不可滑动层。为了简化计算，将挡土墙强度模型也设置为摩尔库伦模型。考虑到随着降雨类型以及降雨强度的不同，边坡会表现出浅层局部以及深层整体两种滑动类型，对弃渣体边坡采用指定滑动面位置的方法分别从其局部以及整体两个方面进行分析研究。即指定局部以及整体两个滑面的大致范围，由软件在此范围内分别自动搜索得到两个最危险滑面，局部滑动面以及整体滑动面能够代表降雨对浅层滑动以及深层滑动两种滑动形态的影响程度。图8为滑动面位置示意图，为了研究暂态饱和区分布与边坡稳定性之间的联系，将暂态饱和区的发展划分为：坡脚开始饱和阶段、坡顶全饱和阶段、坡顶消散阶段、坡脚暂态饱和区消散4个阶段。4个阶段的时间节点分别对应2.0，3.0，25.5，26.0 h。

降雨对边坡稳定性影响的方式主要有3种：① 降雨导致土质软化，凝聚力c、内摩擦角φ降低;② 随着降雨入渗，雨水填充土体内部孔隙，基质吸力降低，导致边坡抗剪强度降低;③ 雨水渗入坡体，导致其自重增大，增大了下滑力，导致其稳定性降低[13]。

本文在前人研究的基础上，将暂态饱和区发展分布规律与边坡安全系数的变化建立联系进行分析。

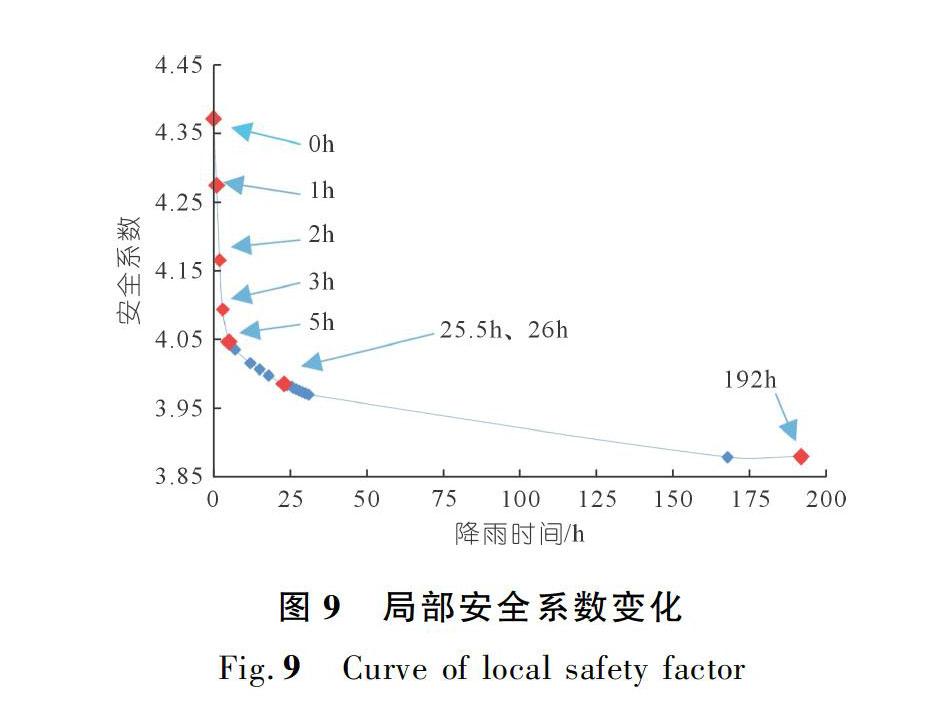
图9的局部滑动面中：在降雨初期（0～2 h），边坡安全系数几乎以匀速降低。而在2～5 h，安全系数降低的幅度是逐渐减小的。在25.5，26.0 h分别为坡顶与坡面暂态饱和区消散的临界时间点，从局部安全系数变化曲线来看，25.5，26.0 h时并未表现出明显的数据突变。在192 h，在雨水长时间的入渗之后，弃渣体边坡安全系数开始恢复。

分析认为：0～2 h时，由于坡面未饱和，所以此时的降雨全部渗入土体，未在坡面汇集形成径流流失。且此时入渗雨水主要集中在坡顶位置，不会出现软化滑动带土体的情况。所以前2 h降雨入渗对弃渣体安全系数的影响主要体现在加大了其自重使下滑力增大。2～5 h时坡面已经达到饱和状态形成暂态饱和区，此时雨水的入渗就变成了有压入渗，且会在坡面形成径流，雨水并非完全渗入土体，此时下滑力的增大趋势变缓，安全系数的下降速率降低。192 h时由于雨水逐渐从坡体内排出（或蒸发），安全系数开始增大。此现象与前文弃渣体边坡稳定性的监测应持续一段时间的建议论相吻合。

图10的整体滑动面中，对比局部安全系数的变化可以发现，局部安全系数、整体安全系数与降雨历时的变化规律与趋势几乎相同，不同点是降雨对局部安全系数的影响更大，整体安全系数的增大点出现的时间更晚。

笔者分析认为：由于整体稳定性的下滑力涉及的土方更多，而降雨对其重度（下滑力）的增大相对于原下滑力较小。由于渗入弃渣体的雨水流出整体滑体需要的时间更长，导致整体安全系数增大点出现的时间相对更晚。两者的变化趋势相同，说明虽然整体滑面和局部滑面涉及的深度不同，但是雨水对该弃渣体整体以及局部安全系数的影响方式是相同的。

综上分析，局部滑动面更容易受影响，所以在对该弃渣场进行治理的过程中应该更多地关注浅层滑动。

结合前面暂态饱和区4个分布阶段的分析，在坡面暂态饱和区形成过程中，边坡安全系数下降速度最快。其中局部安全系数在坡脚开始饱和阶段（2 h）下降速度最快;整体安全系数在坡脚开始饱和阶段（2 h）和坡顶全饱和阶段（3 h）的下降速度相同。

5 结 论

（1） 坡面暂态饱和区并不会随着降雨的停止立刻开始消散。当两层土质渗透系数相差较大时，降雨会沿着层面流动，所以在对弃渣场进行选址时，应考虑场地中不同岩层渗透系数的差异。在该弃渣场已经填筑完成的情况下，应在挡土墙层面位置设置排水孔，疏导层间水流。

（2） 降雨对边坡的影响是一个漫长的过程，降雨停止后的一段时间边坡孔压仍未恢复至正常水平。

（3） 降雨发生期间，影响该弃渣场暂态饱和区分布的只是前3 h;在暂态饱和区稳定形成以后，降雨对暂态饱和区分布的影响显著降低。

降雨期间，饱和区从坡脚逐渐发展到坡顶，而降雨停止之后暂态饱和区的消散是从坡顶向坡脚逐渐消散。

（4） 局部滑动面更容易受降雨的影响，所以在对该弃渣场进行治理的过程中应该更多地关注浅层滑动。整体安全系数恢复更慢，如果需判断弃渣体降雨后的整体稳定性则需延长监测时长。

（5） 前3 h是暂态饱和区形成的过程，安全系数下降速度最快，而当暂态饱和区达到相对稳定状态以后，降雨对边坡稳定性的影响逐渐降低。

参考文献：

[1] 吴谦，毛雪松，刘龙旗，等.某弃渣场边坡稳定性的可靠度分析[J].桂林理工大学学报，2017，37（3）：475-480.

[2] 李叶鑫，史东梅，吕刚.不同恢复年限弃渣场入渗特征研究与评价[J].水土保持学报，2017，31（3）：91-95.

[3] 吴伟东，苟唐巧，许博浩，等.基于改进PPC模型的铁路弃渣场综合风险评价系统[J].中国安全生产科学技术，2019，15（8）：181-186.

[4] 孙朝燚，陈从新，郑允，等.基于空间效应的弃渣场边坡稳定性方法探讨[J].西南交通大学学报，2019，54（1）：97-105.

[5] 聂超，韩文喜，宋柏冰.西南某机场高填方边坡于不同降雨条件下的变形影响[J].科学技术与工程，2018，18（3）：174-183.

[6] 高飞，何京拔，湛汉溪.AutoCAD Civil 3D软件在弃渣场设计中的应用[J].人民长江，2017，48（12）：12-14，41.

[7] 任青文，張林飞，沈雷，等.考虑非饱和渗流过程的岩体变形规律分析[J].岩石力学与工程学报，2018，37（增2）：4100-4107.

[8] 张海阔，姜翠玲，李亮，等.基于HYDRUS-1D模拟的变水头入渗条件下VG模型参数敏感性分析[J].河海大学学报（自然科学版），2019，47（1）：32-40.

[9] 卢玉林，陈晓冉.地下水渗流作用下土坡稳定性的简化Bishop法解[J].应用力学学报，2018，35（3）：524-529，687.

[10] 毛雪松，宋玉品，吴谦，等.渗流条件下弃渣场边坡的稳定性分析[J].兰州理工大学学报.2018，44（2）：139-143.

[11] 曾铃，史振宁，付宏渊，等.降雨入渗对边坡暂态饱和区分布特征的影响[J].中国公路学报，2017，30（1）：25-34.

[12] 蔺港，孔令刚，詹良通，等.基于太沙基土拱效应考虑基质吸力影响的松动土压力计算模型[J].岩土力学，2015，36（7）：2095-2104.

[13] 李宁，刘冠麟，陈有亮，等.降雨诱发浅层滑坡影响因素的解析分析[J].上海理工大学学报，2018，40（1）：65-75.

（编辑：郑 毅）

Study on distribution and stability of transient saturated zone of slope in

abandoned slag yard under rainfall condition

ZHANG Jinmei1，ZHANG Zhen2，LI Jiachun2

（1.Economic and Technological ResearchInstitute，State Grid Yubei Power Co.，Ltd，Beijing 10000，China; 2.Highway College，Chang′an University，Xi′an 710064，China）

Abstract：

In order to clarify the instability mechanism of the slope of the slag yard under rainfall conditions，the abandoned slag yard of a highway from Daozhento Weng′an City in Guizhou Province was taken as a research object.Based on indoor test parameters，we used the SEEP/W module in GEO-Studio to study the distribution of transient saturation zone of abandoned slag yard slope under rainfall conditions and also applied the SLOPE/W module to obtain relationship between slope stability and the distribution of transient saturation zone.It is concluded that：①The effect of rainfall on the stability of the slag slope will last for a long time even after the rain stops.During this period，the safety factor will continue to decrease and finally reach the minimum value.②It takes only a short period for the slope transient saturation zone to develop to the whole slope，during which the slope safety factor declines fastest.After the formation of the transient saturation zone on the slope，the influence of rainfall on the stability of slope is significantly reduced.

Key words：

abandoned slag yard;transient saturation zone;slope stability;unsaturated soil;matrix suction