多车场多车型电动汽车路径优化研究

张惠珍，姜 晶

（上海理工大学 管理学院，上海 200093）

0 引言

车辆路径问题（Vehicle Routing Problem，VRP）作为一个经典的NP-hard 问题，研究最早开始于20 世纪50 年代末［1］。VRP 问题如今已不是单纯的理论研究［2-6］，所需要考虑的因素越来越多，因此根据其特性可将其分为很多种，其中，开闭合车辆路径问题、有容量（比如配送中心、车辆）约束的车辆路径问题、带时间窗的车辆路径问题、考虑周期性的车辆路径问题、多配送中心或单配送中心的车辆路径问题、考虑货物类别和客户满意度的车辆路径问题、新能源汽车车辆路径问题等是目前比较常见的车辆路径问题。随着现代物流业的崛起，新型的VRP 问题不断涌现，使其更具有研究价值和现实意义。揭婉晨等［7］用精确算法求解了多车型电动车车辆路径问题；文展等［8］使用改进的粒子群算法求解带时间窗的车辆路径问题，通过对垃圾回收运输实例的分析，说明相比其他算法，改进后的粒子群算法能够更有效地减少路径距离；孔继利等［9］根据汽车的能源消耗和污染情况研究绿色车辆路径问题；辜勇等［10］通过将多配送中心转换成单配送中心的方式，并且使用三阶段算法求解带时间窗的多中心半开放式车辆路径混合问题，能够高效解决大规模的多配送中心路径问题；Yu 等［11］在CVRP 的基础上研究了通过第三方物流参与的开放式选址车辆路径问题（Open Vehicle Routing Problem，OVRP），其与CVRP 的不同之处在于车辆在服务完所有客户之后，不用返回配送中心，并提出一种基于模拟退火的算法求解该OLRP 问题，该算法可求解最多318 个客户、4 个配送中心的车辆路径问题；Amine 等［12］提出一种基于变邻域搜索的混合算法求解带时间窗的车辆路径问题。

虽然国内外学者已针对使用不同车型进行配送的车辆路径问题进行了大量研究［13-18］，但将电动汽车应用于物流行业尚处于初级阶段［19-22］，研究多车场多车型电动汽车车辆路径问题的文献几乎没有。本文在揭婉晨等［7］的基础上，利用启发式算法代替精确算法对多车型的电动车车辆路径问题进行研究，与揭婉晨等的研究相比，本文能够在较短时间内对大规模算例进行求解，并求得最优解。针对多车场多车型电动汽车车辆路径问题，本文在配送线路内增加了邻域搜索对蚁群算法进行改进，用于求解多车场多车型电动汽车车辆路径问题［11，23-24］，然后采用数值实验进行仿真优化，最后通过算例测试验证了该算法的可行性与有效性，能够在较短时间内对较大规模的多车场多车型电动汽车车辆路径问题求得最优解，为多车场多车型电动汽车车辆路径问题提供了一种新的解决方案。本文采用二阶段算法（Two-phase heuristic algorithm，2-phase HA）对模型进行求解，二阶段算法的主要优势在于对第二阶段蚁群算法的改进，可在给定范围内使用轮盘赌法随机进行变动，并通过增加邻域搜索算子的蚁群算法对MDHEVRP 问题进行求解，得到该问题的最优解，从而使蚁群算法扩大了可行域搜索范围，尽可能避免算法过早陷入局部最优，提高了算法收敛速度。

1 问题描述及数学模型

1.1 问题描述

多车场多车型电动汽车车辆路径问题（Multi-depot Heterogeneous Electric Vehicle Routing Problem，MDEVRP）是指某企业有若干配送中心，每个配送中心有多种不同类型的运输车辆，并且每辆电动汽车的容量都有所限制，每辆电动汽车有一个最大的单次行驶里程，车辆运输成本与运输距离成正比。同一个客户可由多辆车提供服务，且客户需求量已知。每辆车属于一个配送中心，从该中心出发，需要在客户规定的时间窗内服务客户，服务完成后回到该中心。电动汽车从配送中心出发时电量是充满的状态，在行驶过程中会消耗电量，在必要时需到换电站更换电池，之后继续服务客户，直到服务完成后回到配送中心。该研究的最终目的是为每辆车规划合理的路径，使企业的物流成本最低。

1.2 模型假设

假设某企业有m 个配送中心，每个配送中心有n 种类型的电动运输车辆，并且车辆容量有所限制，每辆电动汽车都有一个最大的单次行驶里程，车辆运输成本与运输距离成正比。每个客户只能由一辆车提供服务，且客户需求量已知。每辆车属于一个配送中心，电动汽车从配送中心出发时电量是充满的状态，在行驶过程中会消耗电量，在必要时需到换电站更换电池。要求同一辆电动汽车经过同一充电站不超过一次，更换完电池后继续服务客户，直到服务完成回到配送中心，且电动汽车只能在配送中心或换电站进行充电。

1.3 模型参数说明

M：配送中心集合，M=｛1，2，…，m｝；F：换电站集合，F=｛m+1，2，…，m+f｝；N：客户集合，N=｛m+f+1，2，…，m+f+n｝；V：N∪M∪F，V=｛1，2，…，m+f+n｝；K：车辆集合，K=｛1，2，…，k｝；qj：客户j 点的需求量；Uk：车辆k 的最大可载量；Q：电动汽车电池最大容量；第k 辆车到达i 点之后的剩余电量（kwh）；第k 辆车离开i 点时的剩余电量（kwh）；h：电动车行驶过程中的耗电率（电动汽车每行驶1km 路程所消耗的电量，kwh/km）；dij：i 点到j 点之间距离；C0：距离的单位成本（电动汽车每行驶1km 路程所需费用）；Ck：每辆车的成本（每辆电动车所需的固定成本）；C1：更换电池次数的单位成本（即电动车每更换一次电池的费用）；zijk：为0-1 变量，指第k 辆电动汽车从节点i 行驶到节点j 处，即zijk=1，否则zijk=0。

1.4 模型建立

目标是使总成本最低，总成本包括车辆路径费用、车辆使用费用以及电池更换费用。约束1 表示每个客户都有一辆车为其服务；约束2 表示同一电动汽车进入同一充电站的次数不超过一次；约束3 表示车辆到达同一节点的次数和离开该节点的次数相同，即表示从配送中心离开的车辆必须回到配送中心；约束4 表示为客户服务的车辆总数不能超过配送中心拥有的车辆总数；约束5 表示每辆电动汽车载重量不能超过其最大载重量；约束6 表示电动汽车两点之间的电量约束，必须保证电动汽车有足够的电量到达下一节点；约束7 表示电动汽车离开配送中心和换电站时电量为充满状态；约束8 表示电动汽车在客户点处停留时是不耗电的；约束9 中zijk为0-1 变量，值为1 时表示第k辆电动汽车从i 点行驶到达j 点。

2 算法

2.1 编码方式

本文所求问题的解采用实数编码，将问题的解编为M+F+N 的自然数染色体串，每条染色体都由若干子串组成，每个子串表示一条车辆路径。子串解如图1 所示，其含义为车辆从某一配送中心出发，按顺序逐个访问配送路径上的客户点，最后返回该配送中心。其中，M 为候选的配送中心点数量，F 为候选的换电站数量，N 为客户点数量。在该示例中共有32 个节点，其中配送中心点数量为2（M=2），候选的换电站数量为10（F=10），客户点数量为20（N=20），通过MATLAB 计算得出问题的解。

Fig.1 Expression of substring solution图1 子串解表达

根据MDHEVRP 问题所求出解的编码方式如图2 所示，图中给出了一条完整的车辆路径方案，从该方案中可看出车辆从配送中心出发，并且最终需要回到配送中心。该解表示有两辆车分别从1 号配送中心和2 号配送中心出发，其中一辆车的路径为1-14-16-29-17-27-31-19-25-23-1，该车从1 号配送中心出发后在途中会为9 位客户提供服务。另一辆车的路径为2-13-21-24-18-30-28-6-20-6-20-26-15-22-32-2，由于路程较长，电动汽车的电量不足以完成整条路径上的配送服务，因此电动汽车会在配送途中进入6 号换电站更换电池，最后服务完单条路径上的所有客户后回到2 号配送中心。综上所述，将会有2 辆车从配送中心出发，电动汽车在配送服务过程中会经过6号换电站更换电池，共为20 位客户提供配送服务，服务完成后回到各自的配送中心。

Fig.2 Example of vehicle route solution图2 车辆路径解示例

2.2 K-means 聚类算法

初始解质量不仅会影响问题解的求解质量，还会影响求解速度。为了更快、更好地得到问题最优解，本文使用两阶段算法对MDHEVRP 问题进行求解［25，26］，从而获得初始解。第一阶段使用K-means 聚类算法将所有客户分配到各自的配送中心，因为在K-means 聚类算法初始阶段要选取k 个节点作为初始聚类中心，然后在此基础上进行n 次迭代。因此，选取的节点不同，聚类结果即可能有所不同。K-means 算法的聚类结果对初值较为敏感，算法对初值的依赖性导致聚类结果不稳定。因此，对K-means 聚类算法初始聚类中心选取方法进行改进是非常必要的。第二阶段为每组客户建立合适的TSP 路线。具体步骤如下：

（1）选取所有配送中心节点（k 个）作为初始聚类中心。

（2）首先，计算每个客户点分别到k 个聚类中心的距离，将该点分配到最近的聚类中心，分配完成之后根据式（11）计算各个类的重心，从而得出新的聚类中心。其中，n代表各类中所有节点个数，c 代表每个聚类中的所有节点集合。

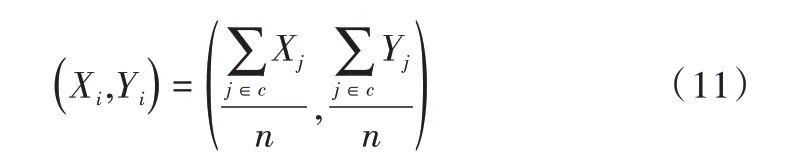
（3）进行多次迭代得到新的聚类中心，以及分配到各聚类中心的节点。

（4）根据两点之间的距离公式（12）计算每个配送中心（k 个）到所有聚类中心（k 个）的距离。

（5）根据Wi值选择聚类中心可替代的配送中心，根据Wi值从大到小的顺序对每个聚类中心重新进行排列。对每个聚类中心依次选择Wi值最大的配送中心，如果该配送中心已选择，则选择Wi值第二大的配送中心，以此类推，直到所有配送中心选择完毕。

（6）重新计算每个客户点分别到k 个配送中心的距离，将该点分配到最近的配送中心。

（7）为每组客户建立TSP 路线。计算每组待访问客户集中每个客户到各自配送中心的距离，随机挑选一个客户作为该条路线上的第一个客户，然后将该点从待访问集中删除，并选择待访问集中离该点最近的一个客户作为下一个访问客户。每增加一个客户，计算当时的车辆容量及电动车所剩电量，如果同时满足两个要求，则继续选择下一个客户，并将已分配客户放入禁忌表。若不满足车辆容量要求，则插入这条路径开始的配送中心编码。如果还有未访问客户，再重新插入该组客户的配送中心编号，启用一辆车进行一条新的路径规划。若不满足电量要求，则随机选择一个最近的电动车换电站更换电池，然后继续行驶，直到分配完所有客户。按照分配顺序为已安排的客户建立TSP 路线，即为初始解。

2.3 改进的蚁群算法

蚁群算法一次迭代过程中主要包括信息素更新规则和移动规则［23，27］。

2.3.1 转移概率

转移概率计算方法如式（14）所示。

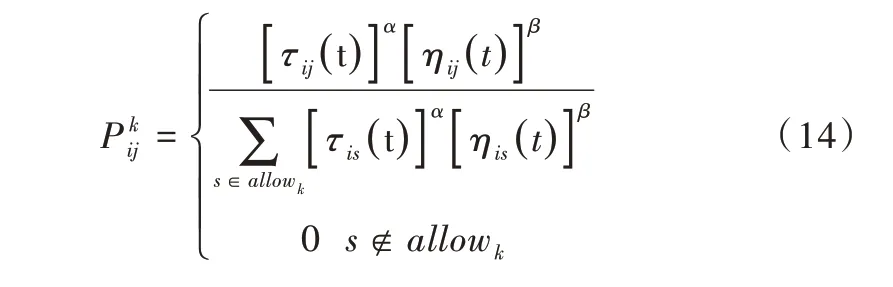
其中，ηij(t)为启发函数，表示蚂蚁从城市i转移到城市j的期望程度；allowk为蚂蚁k待访问城市集合；禁忌表tabuk用于存储蚂蚁k 已访问过的城市，tabuk=N-al⁃lowk；α为信息素重要程度因子，该值越大，表示信息素浓度在转移过程中所起作用越大；β为启发函数重要程度因子，其值越大，表示启发函数在转移过程中所起作用越大，即蚂蚁会以较大概率转移到距离近的城市。

2.3.2 轮盘赌法

为了保证路径的多样性，采用轮盘赌法以加大算法搜索能力，轮盘赌法具体步骤如下：

（1）根据转移概率公式（14）计算出群体中每个个体适应度f(xi)，xi∈allowk。

（2）根据公式（15）计算出每个个体被遗传到下一代群体中的概率。

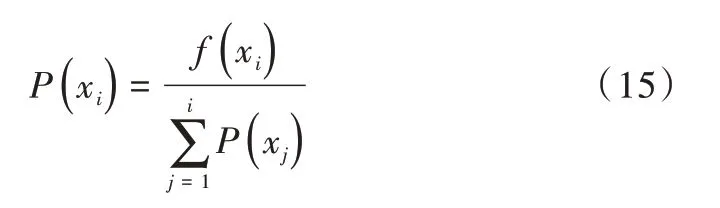
（3）根据式（16）计算出每个个体的累积概率。

（4）在［0，1］区间内产生一个均匀分布的随机数r。

（5）若r≤qi，则选择个体i，否则选择个体k，使得r≤qi成立。

（6）重复d 和e，直到所有客户都被访问。

2.3.3 信息素浓度更新机制

每只蚂蚁在构造出一条从起点到终点的路径后，蚁群算法还要求根据路径总长度更新该路径上所有路径段的信息素浓度。信息素浓度更新机制如式（17）-式（19）所示。

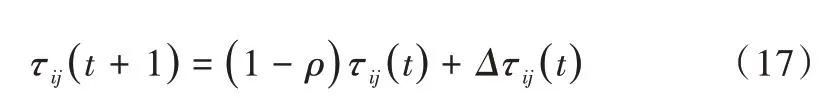
ρ表示信息素挥发程度，信息素浓度随着时间的推移而逐渐减少；Δτijk(t)表示蚂蚁k在从城市i出发到达城市j的路上留下的信息素总量；Δτij表示所有蚂蚁在城市i与城市j 连接路径上释放的信息素浓度之和，其中Q代表信息素常数，表示蚂蚁循环一次释放的信息素总量，Lk代表第k只蚂蚁经过的路径长度。其计算方式如式（18）、（19）所示。

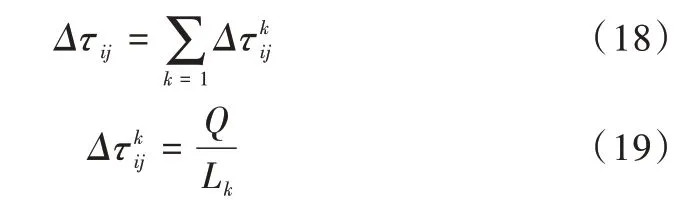
2.3.4 邻域搜索

为防止蚁群算法陷入局部最优，引入单点交换、插入、单点插入、移除和逆转5 种邻域搜索机制，以扩大解空间搜索范围。

单点交换模式：随机选择节点i和节点j两个位置，交换相应的位置编号。

插入模式：随机选择节点i的位置，将换电站编号插入到该节点之后。

单点插入模式：随机选择节点i和节点j两个位置，将节点i的编号插入到节点j的编号之前。

移除模式：随机选择换电站节点i或配送中心节点i的位置，删除换电站或配送中心编号。

逆转模式：随机选择节点i和节点j两个位置，将两个节点间的所有节点反向排列。

根据蚁群算法产生的当前解，分别随机采用以上邻域搜索方式产生邻域解，从而扩大解空间搜索范围。改进后的蚁群算法邻域搜索方式如表1 所示。

Table 1 Neighborhood search methods of ant colony algorithm表1 蚁群算法邻域搜索方式

2.3.5 改进的蚁群算法流程

算法步骤如下：

（1）初始化参数。蚁群算法需要对参数进行初始化，初始化参数是指对相关参数进行初始化，如蚂蚁数量、信息素重要程度因子、启发函数重要程度因子、信息素挥发因子、信息素常数、最大迭代次数等。然后输入数据，计算两点之间的距离。

（2）使用K-means 聚类算法产生初始解，并删除初始解中的配送中心与换电站编号。

（3）候选配送中心选择。重新随机选择一个配送中心作为起点，m 只蚂蚁从各自选择的配送中心出发，并且最终回到各自的配送中心。

（4）根据转移概率公式计算转移概率，确定下一个访问节点，判断节点是否满足约束条件。将已访问客户放入禁忌表，在满足所有约束条件的情况下，在全局路径中插入可选择的配送中心和换电站，将全局路径分为若干局部路径段。

（5）直到所有蚂蚁完成路径搜索，计算各蚂蚁经过的路径长度。

（6）对每只蚂蚁经过的路径进行邻域搜索，计算并保存产生的可行解，比较每个可行解的适应度值，记录当前迭代次数的最优解。

（7）信息素更新。

（8）判断是否满足最大迭代次数。

（9）得到全局最优路径。

二阶段算法流程如图3 所示。

Fig.3 Two-phase algorithm flow图3 二阶段算法流程

3 实例仿真

为了验证算法的有效性，本文对两组规模不同的算例进行测试，测试数据相关信息如表2 所示。

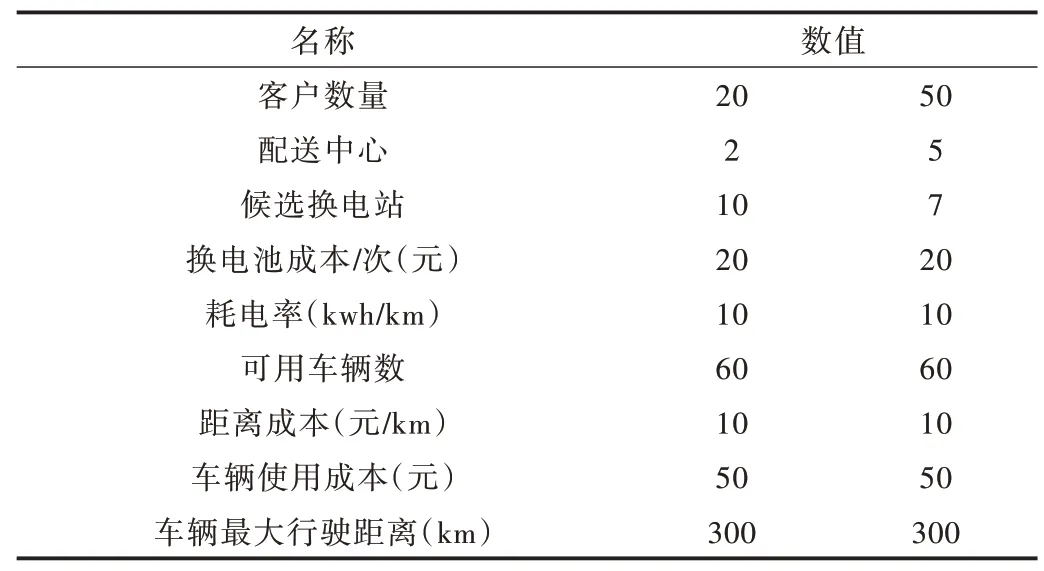
Table 2 The relative data of tested instances表2 测试算例相关信息

本文在Windows10 系统的MATLAB2016a 版本下实现MDHEVRP 问题求解及相关算例验证。对于每一个参数，需要进行多次测试取平均值，本文共运行了10 次。在算法开发过程中发现了一组关键参数，与其他参数相比，这些参数对解的质量影响较大。在测试活动中从基础设置开始，连续细化每个关键参数的值，对每个参数连续测试5个值，保留最佳值作为各参数的最终设置，并继续调整下一个参数。调整后的参数如表3 所示。

Table 3 Parameter setting表3 参数设置

电动汽车类型如表4 所示，共有A、B、C 3 种类型的车辆，其中A 型车辆的车容量为300 kg，单次使用价格为100元，配送中心共有30 辆A 型车辆；B 型车辆的车容量为500 kg，单次使用的价格为150 元，配送中心共有20 辆B 型车辆；C 型车辆的车容量为800kg，单次使用的价格为200 元，配送中心共有10 辆C 型车辆。所有电动汽车的电池类型相同。

Table 4 Vehicle information表4 车辆信息

4 结果分析

增加邻域搜索对蚁群算法进行改进后，采用二阶段算法对算例进行测试，利用MATLAB 计算得出结果。当客户数量为20 时，计算总时间为27.52s，总车辆行驶里程为108.23km，配送车辆为2 辆，配送成本为1 449.8 元。采用改进算法后的对比数据如表5 所示，每辆车的测试路径结果如图4 所示。优化后的结果显示：路径总长度减少了8.3km，使用车辆数减少了1 辆，且总成本降低了133 元。在蚁群算法的基础上，路径距离减少了7%，总成本降低了8.5%。

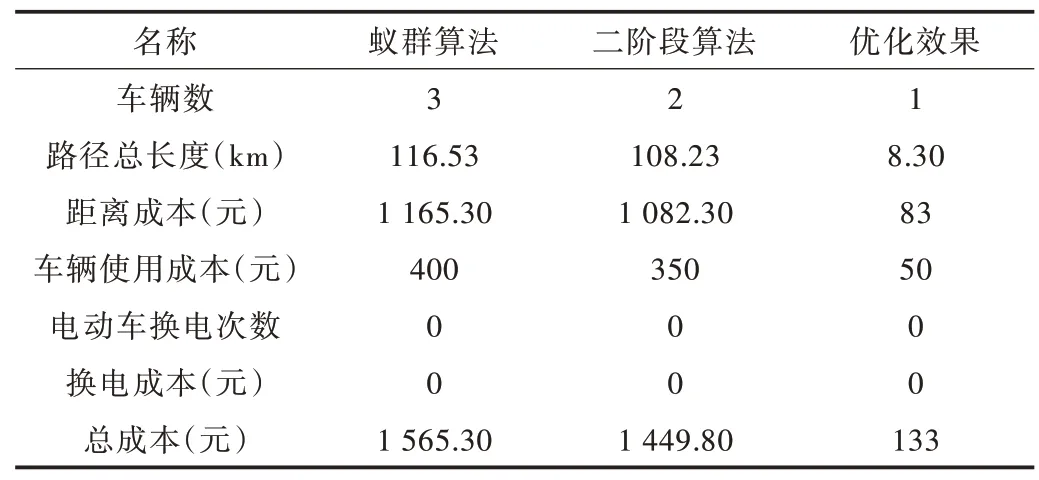
Table 5 Comparison of two-phase heuristic algorithm for 20 customers before and after optimization表5 20 个客户时二阶段算法优化前后对比

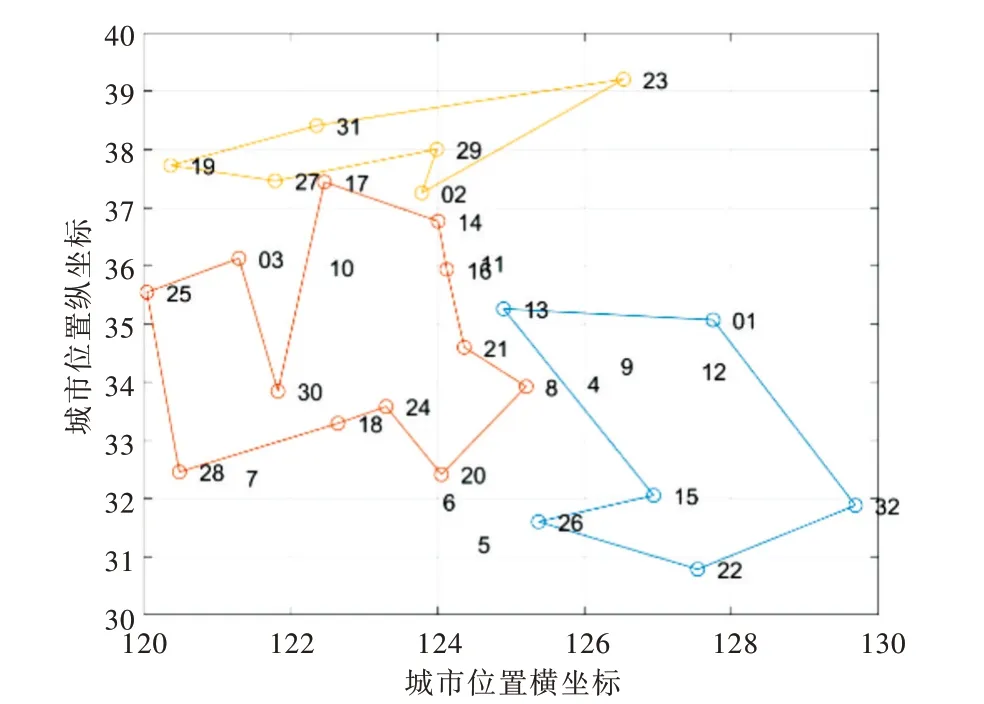
Fig.4 Test route results of 20 customers图4 20 个客户测试路径结果

当客户数量为50 时，计算总时间为79.19s，总车辆行驶里程为66.84km，配送车辆为5 辆，配送成本为1 468.4元。采用改进算法后的对比数据如表6 所示，每辆车的测试路径结果如图5 所示。优化后的结果显示：路径总长度减少了40.13km，总成本降低了351.3 元。在蚁群算法的基础上，路径距离减少了37.5%，总成本降低了19.3%，所以该方案为可行方案。

Table 6 Comparison of two-phase heuristic algorithm for 50 customers before and after optimization表6 50 个客户二阶段算法优化前后对比

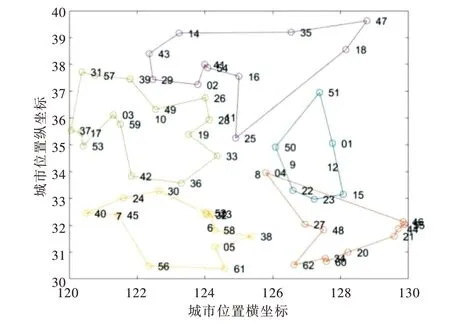
Fig.5 Test route results of 50 customers图5 50 个客户测试路径结果

蚁群算法与改进的蚁群算法性能比较如表7 所示。

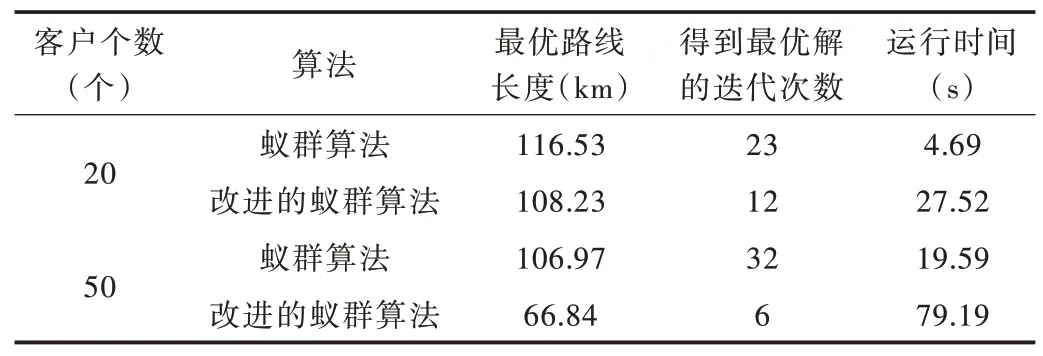
Table 7 Performance comparison of ant colony algorithm and improved ant colony algorithm表7 蚁群算法与改进的蚁群算法性能比较

为进一步验证二阶段算法的求解效率，本文选择CL⁃RP 标准数据库（http：//prodhonc.free.fr/Instances/instancesus.htm）中的6 组数据进行比较。从表8 可以看出，在6 组算例中，GRASP 算法能求出4 最优解，2-phase 能求出5 组最优解，求解正确率为83.33%，相比GRASP 算法提高了16.67%。二阶段算法虽然比GRASP 算法求解时间略长，但也在可接受范围内。尽管二阶段算法只能求出5 组最优解，但其在求解质量上具有一定稳定性，充分说明二阶段算法在求解MDHEVRP 问题上具有良好性能。

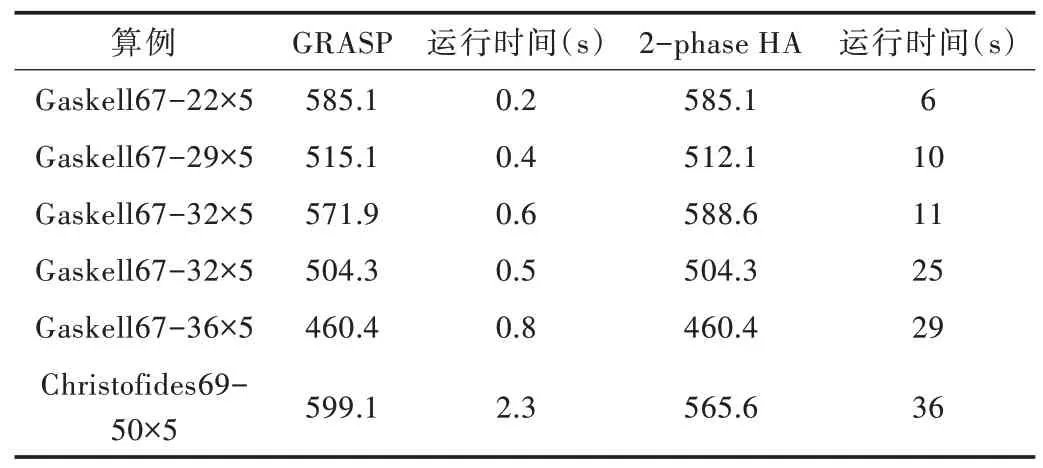
Table 8 Comparative results of model algorithms表8 模型算法效果比较

5 结语

电动汽车的车辆路径问题是现代物流的主要研究方向之一，已受到国内外学者的重点关注。通过研究多车场多车型电动汽车车辆路径问题及其求解算法，可有效地对电动汽车配送路径进行优化，从而降低配送成本、提高车辆使用率、减少资源浪费，进而减少环境污染，并解决目前能源短缺的问题。电动汽车车辆路径问题是一个值得研究的重要课题，但要将电动汽车广泛应用于物流行业还需作进一步研究。可从电动汽车能耗、充电方式及客户所要求的配送时间等方面对电动汽车车辆路径问题进行研究，从而使其能更好地与实际相结合。