教育工作贵在“发现”

周卫东

摘要：结合“紧俏的‘84消毒液可以随便送？”“教材为什么不给出角的定义？”“剪歪了还能求出圆柱侧面积吗？”“两种认识分数的教法怎么都失败了？”四个案例，谈教育工作者在学校管理、备课、上课、教研等工作中应该敏于“发现”。

关键词：教育工作者;学校管理;备课;上课;教研

“紧俏的‘84消毒液可以随便送？”

学校管理方面一则真实的故事，让我记忆犹新。

2020年1月，突如其来的新冠疫情肆虐全国。在延迟开学的那段时间里，教师在家办公，学生居家学习。虽然校园每天都很宁静，但作为校长的我却格外焦虑：正为开学后各种防疫物资的筹措准备而犯愁。我整天想的就是消毒水、口罩、防护服、额温枪等物资，而每天要做的就是奔走于各家超市、“刷”手机淘宝、给各家厂商打电话，可是收效有限，所获甚微。

2020年1月31日，我偶然在微信“朋友圈”里看到了我担任南京市青年教师骨干培训班导师时班上的学员诸梅美校长发的一则消息：“1月31日下午，一位家长来到漆桥中心小学门口，扔下两箱‘84消毒液后便转身离开。朱克卫校长正好站在大门口，来不及问其姓名，只抓拍到匆忙离去的背影。在此，向这位热心家长说一声：谢谢您！感谢家长的支持，感动于家长的付出！家校合力，众志成城，共抗疫情，我们有信心！”

诸校长所在的学校远在南京市高淳区漆桥镇，是一所典型的乡镇中心小学。一个偏僻的鄉镇，紧俏的“84”消毒液可以随便送？我隐约感觉到些什么，随即拨通了诸校长的电话，果不其然：漆桥镇就有生产“84”消毒液的厂，而且厂长就是她舅舅。

第二天，诸校长亲自开车拉着20箱“84”消毒液送到了我校。

后来，我校的消毒液还支持了许多兄弟学校，得到了区教育局领导的表扬。

这份收获和肯定，得益于诸校长的雪中送炭，也庆幸自己对微信“朋友圈”消息的敏锐“发现”。

其实，这样的故事随时都有可能发生，需要的只是我们那双敏于“发现”的眼睛，那颗敏于“发现”的心。

“教材为什么不给出角的定义？”

回到学科教学的话题。在日常备课中，在我与教材、教参来往消磨的时光中，那种因敏于“发现”而带来认识提升的事例，也有很多。

马上要执教一节公开课，课题是四年级的《直线、射线和角》。像惯常一样，我打开了北师大版及其他几个版本的小学数学教材，进行对比分析。

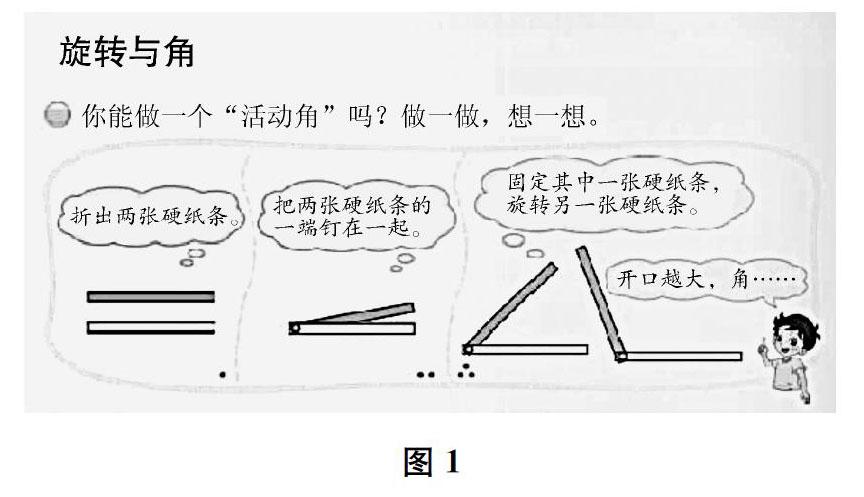
什么是角？北师大版教材没有给角下定义，而是采用了一种活动的方式来研究角（见图1）。与其他版本教材采用的“从一点引出的两条射线可以组成角”和“从一点引出两条射线所组成的图形叫作角”等定义式教学完全不同。

北师大版教材为什么不给角下定义？要不要给角下定义？角的本质是什么？怎样才能让学生理解角的本质？带着这些问题，我走进了有关专著，开启了我的研究之旅。

在张奠宙先生主编的《小学数学教材中的大道理》一书里，我看到了这样的论述：“《几何原本》中，对于角的本质说得很清楚：两条直线相交，如果不重合的话，一条直线相对于另一条直线的倾斜程度叫角。其实，角说的是那个倾斜程度。一点引出的两条射线构成的图形叫角，没有揭示角的本质;一条直线相对于另一条直线的倾斜度，才是角的本质。”这段话给了我很大的启发，让我明白了北师大版教材这样编写的道理，也为我设计实施如下教学提供了支撑。

1.研究。“同学们，经过直线上一点，再画出一条不同方向的直线，可以画几条呢？”引导学生自由创作。

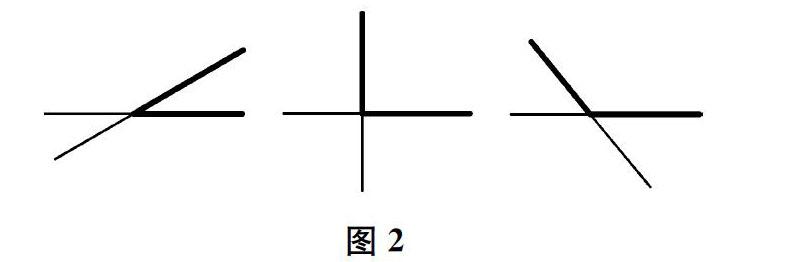
2.对比。呈现学生的代表性作品（如图2），引发思考：“这些作品有哪些一样的地方，又有哪些不一样的地方？”得出：这些作品中都有两条直线，都有一个交点，都有一个角。

3.想象。引导思考：“如果图中这个角固定了，那么，两条直线的位置关系还会变化吗？”得出：角固定了，两条直线的位置关系就不变了。

4.总结。相机揭示：“数学上有这样的一个规定：经过一点的两条直线有着无数种位置关系，为表示它们不同的位置关系，人们想到了研究角，当其中一个角确定了，两条直线的位置关系也就确定了。”

什么是角？从上学时我就熟知它的定义且从教许久也没怀疑过：教材怎么说，我就怎么学，也就怎么教。其实，“从一点引出的两条射线可以组成角”只是角的外在形态，即角的“长相”，而非角的内在本质，即角的“灵魂”。因此，概念的本质除了回答概念是怎样的，也一定会回答为什么是这样的，进而回答还可以是怎样的。

对知识本质的触摸，需要我们常持质疑之心，常用对比之法，常有“发现”的眼光和意识。唯此，教学才会登上一个新的台阶。

“剪歪了还能求出圆柱侧面积吗？”

同样，在日常上课中，在我与学生来往消磨的日子里，那种因敏于“发现”而带来教学增值的故事，更是不胜枚举。

教学《圆柱的侧面积》一课——

[出示苏教版小学数学教材中的例2：“一种圆柱形的罐头，底面直径是11厘米，高是15厘米。它的侧面有一张商标纸（如图3），商标纸的面积大约是多少平方厘米？（接头处忽略不计）”]

师同学们有什么思路？

生把这一圈商标纸剪下来，铺平了，商标纸的面积就是圆柱的侧面积。

师怎么剪呢？

生必须竖直剪，沿着圆柱的高剪。

生这样剪下来就是一个长方形，好算面积。

师为什么剪下来是一个长方形呢？我目前想象不出来，谁来指点我？

生（同步在黑板上画图）底下一圈现在是圆形，剪开后就被拉直了，是长方形的长;因为是沿着高剪的，所以圆柱的高就是长方形的宽。

生其实，圆柱的侧面积和长方体的侧面积差不多，只不过圆柱的底面是圆，圆的周长就是长方形的长，而长方体的底面是长方形或正方形，底面长方形或正方形的周长就是侧面展开长方形的长。

师怎样求圆柱的侧面积？

生用底面周长乘高。

师谢谢你们的指点，我听明白了。那就眼见为实，剪一剪矿泉水瓶的商标吧。

生老师，必须垂直剪，不能歪了！歪了就不是长方形了。

师（作出斜着剪的动作）哦？剪歪了不行吗？

（学生好奇，盯着矿泉水瓶思考。不一会儿，有学生举手了。）

生可以剪歪。即使歪掉了，拉直后不是长方形，也没有关系，因为侧面积的大小不变。

生我来画图吧。（在黑板上画出图4）假如斜着剪，剪下来的应该是一个平行四边形，这个平行四边形的面积还是用底乘高，也就是圆柱的底面周长乘高来计算。

生万一剪的是曲线，怎么办呢？

师（在黑板上画出图5）比如这样剪？

生那就比较麻烦了吧？

生确实麻烦了一点，得把这个不规则的图形转化成长方形，应该是这样的。

（该生在黑板上画出图6。）

师对比一下刚才的3种剪法，你有什么发现？

生不管怎样剪，圆柱的侧面积都是用底面周长乘高来计算。

生我还是觉得剪成长方形更简单一些，因为剪成其他图形还是转化成长方形来求的。

生因为用长方形纸卷成一个圆柱最方便呀！

生但我们不能以为只有这一种方法。

师在探究如何计算圆柱侧面积的过程中，你认为最关键的是什么？

生把曲面变成平面。

生转化。

师说得真好！学习数学需要掌握基本的解题方法，还要尽可能去发现其他情况，从不同的情况中找到相同的思想方法，这样同学们的思维水平就更高了。

上述教学过程中，当学生提出“必须垂直剪，不能歪了”的看法时，我的心里“咯噔”一下：把侧面沿高展开，通过长方形的面积来推导圆柱的侧面积是学生必须掌握的基本推导方法，但它不是唯一的方法，那么，教学要不要往前跨一步？该怎么跨呢？这时，我觉得应该等一等，也许有学生会发现其他剪法。于是，我提出“剪歪了不行吗”的问题。果然，学生有了新的发现，课堂有了新的生成。

好的教学从来不是僵化的照本宣科，而是师生能量、情思的交换。我们追求的不仅仅是基于预设的教学，更是面向学情、应对生成的教学，是一种不断变化着的教学形态。因而，发现意料之外的学情与生成，随之焕发出的必然是朝向儿童教学的应有之义。

“两种认识分数的教法怎么都失败了？”

备课和上课需要“发现”，教研又何尝不需要“发现”呢？

最近，学校教研组开展同课异构活动。小A和小B两位青年教师都执教了《认识一个整体的几分之一》这节课——只进行20分钟的例题教学。但是，两节课上，学生都没有很好地建构分数的再认识。

小A老师先出示一个遮着布的盘子，提问：“盘子里有一些桃，猴妈妈要将它们平均分给两只小猴，每只小猴分得这盘桃的几分之几？”学生齐答：“12。”教师再依次出示第二、第三个遮着布的盘子，提出相同的问题。学生都不假思索地回答：“12。”教师揭示第二个盘子里有4个桃，第三个盘子里有6个桃。“如果有100个桃呢？每只小猴分得它的几分之几？”学生喊道：“12。”小A老师感觉课上得很顺畅，于是追问：“今天再次学习分数，和上学期有什么不同？”大多数学生懵住了，经过教师反复引导，方才有所感悟。最后小A老师布置了一道小练习：有4个圆，平均分成2份，涂色的2个圆是它的几分之几？很多学生写“24”。小A老师很郁闷：例题不是学得很好吗？怎么到后面出问题了呢？

小B老师先出示一盘6个桃，提问：“盘子里有一些桃，猴妈妈要将它们平均分给两只小猴，每只小猴分得这盘桃的几分之几？”有学生发言：“36。”很多学生附和。小B老师提问：“都认为是36啊？有不同想法吗？”话音刚落，认为答案是36的学生强调：“老师您看，一共有6个桃，每只小猴分3个，6个里面取3个，当然就是36。”这番话引来更多学生的附和。小B老师有点发慌，问道：“都赞成他的想法吗？还有没有不同的想法？”还是没有人站出来反对。小B老师只好组织小组交流。一番热闹的小组交流之后，终于有一个男生说：“12？”小B老师立刻放大他的想法，请他说具体些。他说：“把6个桃平均分成2份，每份是12。”小B老师转问其他学生：“你们听懂他的意思了吗？你们还坚持36吗？”“我们坚持！他说的12，不知道一共有几个桃，还是我们说的36好。”小B老师再问那个男生：“你认为呢？”他点了点头说：“我现在也觉得36好。”小B老师无奈地苦笑。20分钟到了，基本的例题教学都没有完成。小B老师很郁闷：怎么全军覆没了呢？

课后，我和两位教师一起做了深入的剖析。我发现，很多青年教师教学时，会先入为主，凭借自己对数学知识的理解设计教学，缺乏对儿童的理解，对学情的洞察远远不够。小A和小B两位老师都以为《认识一个整体的几分之一》一课，只不过是把以前平均分一个物体扩充为多个物体，分数的含义还是一样的，学生应该能自主顺应。但事实并非如此。小A老师的课上，学生三次喊“12”并非因为真正理解分数的含义，而是因为老师只给出了“1”和“2”两个数据。被遮蔽的错误认识迟早会暴露。小B老师满以为直接面对“36”这一错误资源，一定会引发激烈的辩论，使道理越辩越明。孰料，极个别发现真理的人也有猜测的成分，很快就被大多数人说服。

于是，我组织了以“基于学情分析的‘认识分数教学”为主题的系列校本研修，带领教研组深度研究了苏教版小学数学教材设计的分数教学的三个阶段：“分数的初步认识（一）”“分数的初步认识（二）”和“分数的意义”。对每一个课题，我都带领教研组历经大量的学情调研与分析。在青年教师上课的过程中，我及时拍下有问题的片段，指导他们解决问题的基本策略与方法，引导他们敏锐地发现课堂上学情的变化，积极地作出应对。大家都表示，这样的校本教研是基于“真问题”的“好教研”。

好的教研主题从哪里来？一定源于教师真正需要研究和解决的问题。这就需要我们从惯常的“假大空”“走过场”的校本研修怪圈中走出来。教研活动只有多一些针对性和创造性，教师才会多一些实实在在的收获与成长。

思考延伸

在教师日常的管理、教学和研究中，常会出现这样的现象：即使是司空见惯的情况，有的人也能够敏锐地发现问题;反之，即使是极不寻常的情况，有的人也可能发现不了问题。在善于发现的人中，对同一个现象，有的人可能从这一角度发现问题，有的人可能从另一角度发现问题。这是为什么呢？爱因斯坦说过，你能从现象中看到什么，取决于你脑子里有什么理念。理念既是望远镜，又是显微镜。

我们应该持有怎样的理念？说到底，就是一份责任在肩的操守和为了教育的情怀，就是一种扎根学科理解的厚重底色和为了儿童成长的基本立场。

20世纪80年代，美国学者舒尔曼系统地确立起“学科教学知识”这一概念，这是教师学科知識与教育学知识的融合。从它的组成要素来看，“善于洞察教育现象背后的教育价值，使之转化为有效的教育现场并让学生从中受益”，是一项重要的内容。这一内容融合了教师关于学习者的知识、教师的教育理解、教师的个人生活经验与实践智慧、教师的学科知识等诸多要素。

无论是为了新时代教育事业的蓬勃发展，还是为了我们自己管理、教学等工作的高效顺利，让我们都能从敏于“发现”中得到充实、快乐和自在。

参考文献：

[1] 张奠宙，巩子坤，任敏龙，等.小学数学教材中的大道理——核心概念的理解与呈现[M].上海：上海教育出版社，2018.

[2] 杨凯.数学教学要克服前摄抑制——《分数的意义》教学尝试与改进[J].教育研究与评论（课堂观察），2018（4）.教育研究与评论小学教育教学/2021年6月前沿论坛