基于改进遗传的XML注入式攻击自动测试
2021-08-23高建华
王 茜,高建华
(上海师范大学 计算机科学与技术系,上海 200234)
0 引 言
SOA(service-oriented architecture)[1]架构也称面向服务架构,SOA技术的普及与发展使得基于该架构的Web服务安全问题日益突出。SOA架构Web服务安全问题的重要因素就是SOAP消息的传输。由于SOAP传输协议所依赖的WS安全标准存在缺陷,所以在SOAP消息在传输中易受到XML(extensible markup language)[2]注入等一系列针对Web服务的攻击。
基于模糊测试[3]的检测方法可以在满足以下两个条件的情况下检测简单的XML注入式攻击漏洞:①没有检查XML格式和有效性机制;②测试工具可以观察到被测系统的错误响应。然而一些攻击可能来自于多个用户输入字段的组合,所以这就使XML注入式攻击的形式变得更加复杂,检测更加困难。
Julia等[4]通过研究发现,基于污点分析的检测方法会产生许多错误警告,此外该方法生成的跟踪信息有可能包含了许多不相关的信息,存在大量冗余的测试数据。
基于搜索的检测方法能够在有限的空间和时间内找到合适的解,且不受限于系统的规模。主要方法有基于粒子群优化算法[5]的搜索和基于遗传算法的搜索等。但是基于粒子群优化算法的搜索会在执行不久后出现大量粒子聚集的现象,存在过早收敛的缺陷。
由此,本文提出了一种基于改进遗传的XML注入式攻击检测方法。该方法使用实码遗传算法在搜索空间自动搜索用户输入。执行过程中,通过引入影响因子改进适应度函数计算方法,优化适应度函数值和算法的搜索,从而缩短搜索时间,提高搜索效率。
1 相关术语
1.1 XML注入式攻击
与SQL注入式攻击类似,XML注入式攻击是通过将恶意内容注入到用户输入从而通过修改SOAP信息的内容和结构产生恶意XML信息来实现的。恶意的XML信息能够导致目标系统的崩溃,某些XML信息还会威胁到处理恶意信息的系统本身。假设一个Web应用程序的注册表单有3个用户输入字段,分别是用户名、密码和电子邮箱。当用户提交注册页面信息时,应用程序会调用如图1中所示的代码产生相应的SOAP信息并将其发送到服务端。后端服务会通过调用getnewuserid()方法为该注册新用户分配一个唯一的标识码UserId。

图1 SOAP信息
如果此时用户名输入字段为:Tom,密码输入字段为:123456<!-,电子邮箱输入字段为:mail=->

图2 XML消息
Briand等[6]通过研究发现,非恶意的XML消息通过突变操作可以生成4种类型的XML注入式攻击。如表1所示,它们分别是:类型1:变形;类型2:随即关闭标记;类型3:复制;类型4:替换。这4种类型的XML注入式攻击分别使用不同方法生成恶意信息。类型1通过创建格式不正确的XML消息使系统受到攻击;类型2的XML注入式攻击通过带有额外关闭标记来显示XML文档或者数据库的隐藏信息;类型3和类型4旨在更改XML消息造成嵌入式嵌套攻击。

表1 4种类型的XML注入式攻击
1.2 编码模式
本文提出的基于改进遗传的XML注入式攻击自动测试算法旨在搜索能够造成系统受到攻击的所有可能用户输入。如果存在导致被测系统(system under test,SUT)生成恶意XML输出的用户输入,此时被测系统易受到XML注入式攻击。因此,本文将这样的用户输入看作是测试目标。
通常来说,输入字符串的字符可由扩展ASCII码或UNICODE表示,在本文中,只考虑ASCII码32到127之间的可打印字符,因为大多数软件不使用非输出字符。
对于一个给定的被测系统,如果用户页面由N个输入参数组成,则算法的搜索空间可以由Web表单提交的N个字符串的所有可能元组来表示。每个用户输入参数就是一个字符串,每个字符串可由任意字母、数字或者特殊字符的组合。
定义1测试目标:一个给定被测系统的候选测试用例是一个由N个输入参数组成的字符串元组,记作TO
TO={S1,S2,…,SN}
定义2 输入参数:一个给定被测系统的输入参数都是一个由k个字符组成的字符串,记作S
S={c1,c2,…,ck}
定义3测试目标集合:本文的测试目标是经被测系统运行后能够产生XML注入式攻击的用户输入。被测系统不同用户的输入参数个数也有可能不同,其输入参数的长度限制也不同。将系统的用户输入看作是一个集合,称为测试目标集合,记作T
TOs={TO1,TO2,TO3,…,TOn}
定义4注入式攻击集合:注入式攻击由SOLMI[5]自动生成,不同系统的XML注入式攻击有所不同,每个系统生成的攻击会有多个,将同一系统生成的XML注入式攻击看作是一个集合,称为注入式攻击集合,记作T
T={T1,T2,T3,…,Tk}
如果存在用户输入TOi经被测系统执行后,产生恶意XML信息Tj则称该注入式攻击被覆盖则可以表示为:SUT(TOi)=Tj。值得注意的是,测试目标TO和T并不一定是一一对应的,而且TO通过被测系统产生的T必须是满足语法要求并且包含恶意消息的XML信息。
2 基于改进遗传的自动测试
基于搜索的测试在进行搜索时,需解决以下3个基本问题:①选择合适的编码模式来表示测试目标;②选择合适的适应度函数来指导算法的搜索;③选择高效的搜索算法来算搜索测试用例。针对问题①本文在1.2小节中已给出解决方案。
2.1 基于改进编辑距离的适应度函数
针对问题②,搜索的有效性很大程度上取决于适应度函数的指导,适应度函数是对候选测试目标与目标相似度的评估。本文的候选测试目标(也可称作为候选解决方案)是用户输入经过被测系统执行后产生的XML信息,目标是由SOLMI[5]自动生成的XML恶意信息。所以针对本文研究内容,适应度函数值由用户输入经被测系统执行后产生的信息与已知攻击的相似度,即字符串之间的距离决定。
2.1.1 基于实数编码的编辑距离
不同于汉明距离,编辑距离(edit distance,Ed)可以用来比较不同长度字符串之间距离。编辑距离是指将原字符串转换为目标字符串所用的最少编辑操作次数。其中编辑操作包括插入、删除和替换一个字符。
假设有两个字符串An=a1a2…an和Bm=b1b2…bm,则字符串编辑距离可定义为如下递归关系
(1)
其中,an是字符串An中第n个字符,同理bm是字符串Bm中第m个字符。如果an,bm匹配,则f(an,bm)的值为0,否则值为1。
由此,考虑以下问题I:
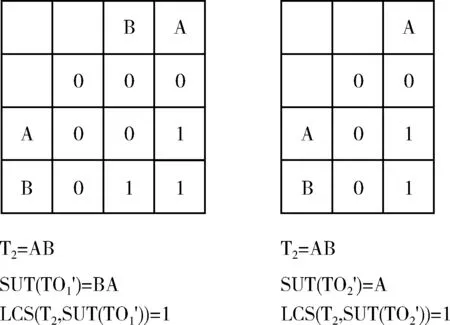
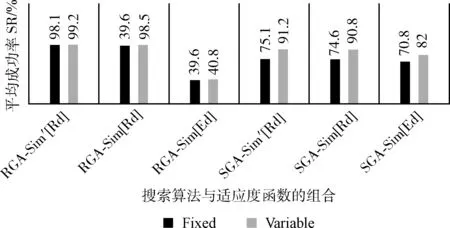
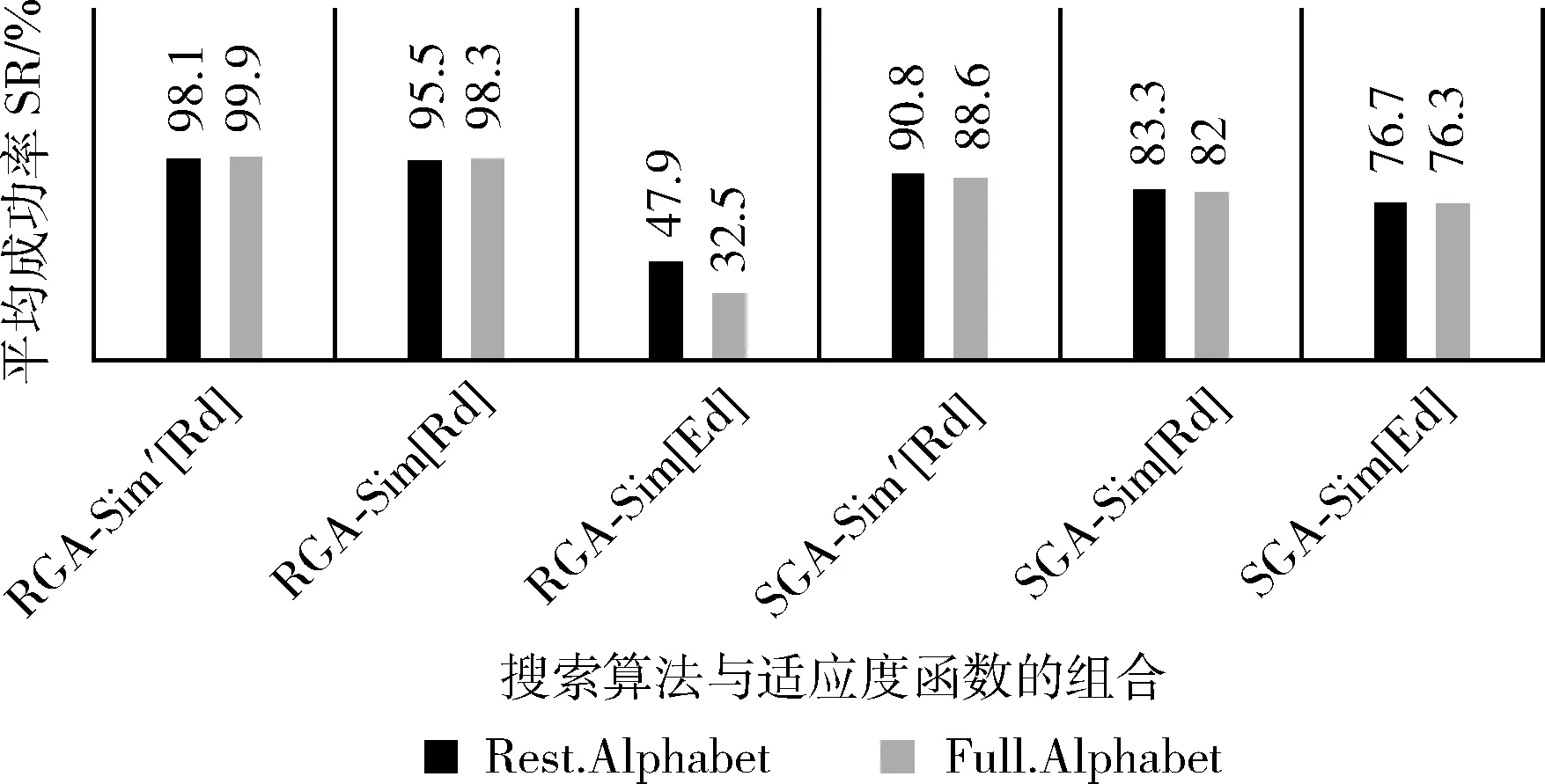
假设一条XML注入式攻击信息为T1= Ed(T1,SUT(TO1))= Ed(T1,SUT(TO2))= Ed(T1,SUT(TO3))=1 因为传统编辑距离只考虑操作次数,所以在这种情况下无法具体区分3个候选解决方案与目标的距离。为了解决这种情况,本文将搜索的重点放在目标领域的子区域上并提出了改进方案。在编辑距离的基础上提出了实码编辑距离[7](real-code edit distance,Rd),将式(1)中的f(an,bm)替换成字符之间的ASCII码的相对距离,则实码编辑距离递归关系定义如下 (2) (3) φ(x)=x/(x+1) (4) 由式(2)重新计算问题I中各个候选解决方案与目标的距离可以得出,最终3个候选解决方案经过被测系统执行后与T1之间的距离别为0.83,0.97和1 Rd(T1,SUT(TO1))=0.83 Rd(T1,SUT(TO2))=0.97 Rd(T1,SUT(TO3))=1 如图3所示,图3(a)、图3(b)分别表示编辑距离和实码编辑距离两种距离算法。针对问题I,从图3中可以看出,图3(b)的实码编辑距离能够更加精确地区分候选解决方案执行后与目标T之间的距离,换句话来说,相对于传统编辑距离,实码编辑距离可以使搜索算法拥有更广的搜索邻域。 图3 两种距离算法对比 2.1.2 改进的适应度函数算法 大部分遗传算法使用目标函数作为适应度函数,适应度函数的设计直接影响了遗传算法的性能。这种适应度函数虽然简单直观,但是某些待解决问题的函数值可能彼此相差较大,这种简单的适应度函数求解不利于群体的平均性能,影响了算法的效果。 常见的基于编辑距离的相似度计算式(5)定义为 (5) 在本文中,适应度函数可以直接由字符串间距离带入式(5)得到,距离越小适应度函数值也就越大,适应度函数值越大则表示与目标越接近。但是这种适应度函数计算方法没有考虑字符串之间公共子序列对相似度的影响。 文献[8]介绍了最长公共子序列(longest common subsequence,LCS)的概念,为了解决问题II,本文在实码编辑距离的基础上改进了适应度函数的计算公式,将字符串最长公共子序列的长度和第一次出现不匹配字符的位置作为影响因子带入计算得出新的适应度函数计算方法。 Needleman-Wunsch算法[8]是一种动态的编程方法,它可以用来计算最长公共子序列,并且能够找到两个字符串最优全局对齐。假设两个字符串An=a1a2…an和Bm=b1b2…bm,通过式(6)可以得出算法矩阵,并通过回溯找出匹配字符串 (6) 通过引入影响因子LCS和第一次出现不匹配字符的位置p,本文重新定义适应度函数式(7)如下 (7) 重新考虑问题II,首先由式(6)计算得出BA和A与T2的Needleman-Wunsch算法矩阵,如图4所示。 图4 LSC矩阵 再将LSC值带入式(7)即可得出 Sim′(T2,SUT(TO′1))=0.4 然而在自然语言处理以及数据挖掘等领域中,要将处理的语句转化为逻辑表达式,这种转化过程需要提取大量的特征并将实体映射到知识库。这里的特征可以来自多个不同的维度。如数据分析模型中,需要通过用户行为来分析用户价值相似度或者使用用户对内容的评分来区分用户兴趣的相似性等情况。这里的相似度评估不仅仅是计算字符串之间的距离,而来自于用户相关操作等多个维度。在这种情况下,欧氏距离和余弦相似度的优势得以体现。本文提到的基于改进编辑距离算法的应用需要进一步的研究和验证。 确定好编码模式和适应度函数,就可以用搜索算法来搜索解决方案,文献[9]中提出了各种搜索算法来解决软件工程问题。传统的搜索算法有随机搜索算法(random search,RS),(hill climbing,HC)算法,标准遗传算法(standard genetic algorithm,SGA)。 SGA标准遗传算法是一个模拟自然进化得到最优解的过程。SGA模拟了自然选择和自然遗传过程中发生的繁殖、交配和变异现象,并通过适者生存、优胜劣汰的自然法则产生新的群体,并比较个体,不断迭代最终得到最优解。SGA算法是一种全局搜索算法,它有效地解决多模态问题。因为使用多个解决方案来采样搜索空间,这可能会导致搜索过程的偏差。另一方面,与HC相比,局部最优收敛速度较慢。因此,对于单模问题,它的有效性和效率通常较低。所以本文针对标准遗传算法的问题在处理单模问题时收敛速度和效率的局限性提出了改进的解决方案。 为了解决以实数或整数作为决策变量的数值问题,本文提出使用实码遗传算法,采用实数编码可以大大提高计算的精度和计算效率。与标准遗传算法不同的是,本文中的实码遗传算法在交叉算子和突变算子上的设计不再是对字符进行直接操作,而是对相应字符的ASCII码进行操作,实码遗传算法与标准遗传算法区别之处在于交叉和变异算子的选择。如表2所示实码遗传算法的交叉选用算术交叉,变异选用高斯变异。 表2 遗传算子对比 二元竞赛选择算子,在进行交叉和变异之前,先将每个字符替换为相应的ASCII代码,再将输入字符串转换为整数数组。 ai′=ai·ρ+bi·(1-ρ) (8) bi′=bi·ρ+ai·(1-ρ) (9) 其中,ρ是0到1之间的随机数,最终的ai′和bi′通过四舍五入取最接近的整数值。 高斯突变与标准遗传算法中的均匀变异类似,种群中的每个测试目标TO都是通过在相应的字符数组中删除、替换或添加字符来进行变异。不同的是,高斯突变处理的是数值数据,这些数值被替换为其它数值的同时遵循高斯分布[11]。假设C={c1,c2,c3,…cj,…,ck} 作为突变的ASCII码数组,数组中随机位置j的元素会被替换成新的ASCII码,并且数组中每个位置突变的概率都相等,数组中元素被替换遵循式(10) cj*=cj+cj·δ(μ,σ) (10) 其中,δ(μ,σ)是正态分布随机数,平均数μ为0,方差是σ。同样最终高斯突变产生的数值取相近的整数值,如果产生的数值不是32到127范围内的可打印字符则取消本次突变。 结合改进的适应度函数算法和基于实数编码的遗传算法,本文提出的算法整体框架流程如图5所示: 图5 核心算法流程 (1)初始化:设置种群大小,交叉概率Pc,突变概率Pm,最大的迭代次数max_propagate; (2)计算适应度函数值:使用基于改进编辑距离的实码编辑距离计算字符串之间的距离,并用式(7)通过引入影响因子计算得出适应度函数值。 (3)选择:二元竞赛选择按照适应度值选择优秀个体; (4)交叉:使用算数交叉对选择的个体进行重新组合,产生新的个体; (5)突变:高斯突变进行变异操作,产生新的种群; (6)判断:若到达终止条件,退出算法,否则跳转(2),继续进行下一次迭代。 本文提出的基于改进遗传算法的自动测试,解决了SGA在单模问题上有效性和效率通常较低的问题,并且通过基于改进的编辑距离的适应度函数算法优化了搜索的精确度,提高搜索的效率。 为了验证适应度函数和搜索算法的有效性,本文在JMetal上实现了测试工具的开发,本文实验硬件环境为Intel Core i5 2.5 GHz处理器,8 GB内存。实验在Windows10操作系统下完成,使用Java编程语言。工具由测试用例生成器和测试执行器两个部分组成。核心组件测试用例生成器用来搜索用户输入,测试用例执行器在测试用例生成器和被测系统之间提供接口,提交由测试用例生成器产生的输入给被测系统,被测系统生成对应的XML消息由执行器截获并转发给测试用例生成器并评估适应度函数得分。为了验证通用性,本文在两个规模不同的系统上进行了实验。 首先在渗透测试演练系统MCIR(magical code injection rainbow)上进行实验。XMLMao是MCIR中的是一个开源的应用程序,它是能够构建可配置脆弱性测试平台的框架,可以接收单个用户输入并产生相对应的XML信息。 其次设计了一个模拟仿真的银行系统SASB(security analog simulation BANK),仿真系统实现了简单的HTML表单和输入处理例程,并且有3个用户输入字段。并且SASB带有对用户输入参数的验证。 在实验中,本文将适应度函数和搜索算法的组合看作独立变量来研究它们对实验的影响。实验内容将适应度函数和搜索算法看作是一个组合来评估它们的有效性,实验研究了两种搜索算法(SGA和RGA)和两种不同适应度函数算法下(Sim[Ed],Sim[Rd]和Sim′[Rd])组合的有效性。(Sim[Ed]表示使用编辑距离和式(5)计算适应度;Sim[Rd]表示使用实码编辑距离和式(5)计算适应度;Sim′[Rd]表示使用实码编辑距离和式(7)计算适应度)。 为了验证算法的有效性,方便评估实验。本文定义成功率函数SR(success_rate),式(11)中的Successful_runs代表了攻击被覆盖的次数,Total_runs代表的是运行总次数。成功率函数SR的数值越大,组合对测试目标的搜索的效果越好 (11) 另外,为了描述成功率的离散性,本文用式(12)来计算SR的标准差SD(standard deviation),标准差函数越小组合的稳定性越好。其中N是同一组合中测试目标的个数,SR是组合中某一测试目标的成功率,μ是组合中所有测试目标成功率的平均值 (12) 搜索算法执行时各参数值具体设置如下: 突变概率:文献[7]证明了基于种群大小和染色体长度的突变概率Pm值可以获得更好的性能,因此本文的RGA和SGA采用式(13)作为突变概率。其中λ是种群大小,l是种群中染色体(测试目标)的长度 (13) 交叉概率:文献[12]提到交叉概率Pc的最佳范围在0.45和0.95之间,本文的实验中选取0.70作为交叉概率。 种群大小:本文设置种群规模为50,此值也与基于搜索的软件测试[13,14]研究中使用的参数设置一致。 本文的研究涉及到以下几个问题: Q1:XML注入式攻击的最佳搜索算法是什么? 针对这一问题,本文比较了两种搜索算法分别在3种不同适应度函数算法的指导下对测试目标的搜索。 Q2:XML注入式攻击的最佳适应度函数是什么? 针对这一问题,本文主要比较3种不同适应度计算方法分别应用在两种搜索算法时对实验的影响。 本文除了研究适应度函数和搜索算法对实验的影响,还研究了另外两个可能对实验有影响的因素:字母表的大小和遗传算法中初始种群个体长度的限制。 假如已知攻击T中不包含字符“A”,那么就可以认为字符“A”不会出现在可以导致XML注入式攻击的用户输入中,所以可以通过忽略这些不出现在已知攻击中的字符来限制字母表的大小从而减少搜索空间。 在搜索测试目标时,所有的搜索算法都是从一组随机生成的解开始的,如果随机生成的字符串与最终的解决方案相比太长或者太短,每次处理这些字符串时就会耗费更多的时间。所以考虑以下两种设置:①生成具有固定(Fixed简称F)最大长度的字符串;②或者生成可变(Variable简称V)长度的字符串。 Q3:字母表的大小是否会对算法的搜索有影响? 针对这一问题,本文将对使用全字母表(Full.Alph)和限制字母表(Res.Alph)进行对比实验,并分析得到结果。 Q4:遗传算法初始种群中字符串的长度限制是否对算法的搜索有影响? 针对这一问题,本文将对遗传算法初始种群的字符串长度采用两种不同限制条件进行对比实验,分别是:字符串定(F)长和可变(V)长。 根据上述问题中涉及到的影响因素,设计了不同约束条件的测试目标,实验Id(Exp.Id)根据应用程序(App)、用户输入参数个数(Inp)、初始种群输入字符串的长度(PopLen)以及字母表是否受限制(Res.Alph)来命名的。例如,SASB中,有2个用户输入并且是可变长,全字母表的测试用例ID定义为S.2.V.F,以此类推,针对不同被测系统,实验设计了16种不同约束条件的测试用例,并分析影响搜索结果的约束条件。 表3总结了XMLMao系统中各组合的实验结果,表中列出了各组合的成功率(SR)、标准差(SD)和执行时间(execution time,ET)的数据,其中执行时间的单位是分钟。在只有单一用户输入的XMLMao开源系统中,RGA算法在搜索成功率方面明显优于SGA,其中RGA在使用Sim′[Rd]和Sim[Rd]指导搜索时的成功率可以达到100%。再对比执行时间数据,可以发现无论是RGA还是SGA在使用Sim′[Rd]指导算法搜索时,执行时间都是最短的,Sim′[Rd]指导RGA平均用时0.92 min,指导SGA搜索平均用时5.64 min。总结得出,Sim′[Rd]指导下的RGA搜索效率较高。 表3 XMLMao中组合的成功率、标准差和执行时间数据 为了验证算法的通用性,实验收集了在模拟仿真系统上的数据并加以分析。该系统有3个用户输入字段,并结合用户输入字段个数、字符长度限制和字母表限制等约束条件定义了以下12种不同限制条件下的搜索实验。如表4所示,在有3个用户输入字段的SASB系统中,RGA算法的搜索成功率明显高于SGA算法,在Sim′[Rd]指导下的RGA成功率可以达到96%。同样Sim′[Rd]指导下的SGA只有69%。同样是RGA搜索算法的前提下,Sim′[Rd]指导的搜索成功率高于其它适应度函数指导的搜索,并且拥有最短的执行时间,平均时间约为3.36 min。总结得出,在有多个用户输入的系统中,搜索成功率虽然不能达到100%,但是Sim′[Rd]指导的RGA依旧在搜索效率上表现出优势,在实码遗传算法的搜中相比Sim[Ed]成功率提高了83.3%,而且拥有更短的执行时间。 表4 SASB中组合的成功率、标准差和执行时间数据 为了更加清晰地分析字母表和初始种群字符串长度限制因素对搜索的影响,本文使用图的形式描述实验数据。图6描述了XMLMao和SASB两个系统中初始种群和字母表限制因素对实验搜索平均成功率数据。从各组合数据中可以看出,当初始种群中字符串长度可变时,成功率高于字符串定长限制,成功率最高可提升16.2%。 图6 字符限制因素成功率对比 图7给出了字母表限制约束条件下的两个系统的平均成功率数据。分析图中数据可以得到结论:在字母表现制约束件下,使用限制字母表的搜索成功率高于全字母表限制,成功率最高提升了15.4%。结合两图6和图7的数据可以得出结论:在搜索测试用例时,设置初始种群字符串长度可变,并限制字母表可以得到更高的成功率,有助于提高搜索算法的搜索效率。 图7 字母表限制因素成功率对比 本文针对XML注入式攻击提出了一种改进遗传的搜索算法,用来搜索对系统造成XML注入式攻击的用户输入。实验结果表明,基于改进编辑距离的适应度函数可以有效地指导实码遗传算法的搜索,可以一定程度上缩短测试程序的运行时间,提高搜索效率。未来的研究内容可以将该搜索算法应用到对SOA架构Web应用程序的WSDL文档解析方面,通过增加约束项目等方法解析WSDL文档生成并优化测试用例集,在保证测试的前提下减少测试用例集的冗余,提高系统抵御攻击的能力并应用在更大更复杂的系统中。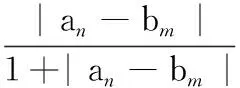

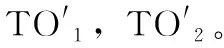
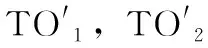

2.2 基于实数编码的遗传算法



3 实 验
3.1 实验环境与参数的配置
3.2 变量的选择
3.3 参数设置
3.4 研究问题
3.5 实验结果分析


4 结束语
