考虑风电机组超速减载与惯量控制的电力系统机组组合策略

2021-08-23蔡国伟杨德友

电力系统自动化 2021年16期

蔡国伟，钟超，吴刚，杨德友，王博

（1.东北电力大学电气工程学院，吉林省吉林市 132012；2.国网吉林省电力有限公司，吉林省长春市 130021）

0 引言

随着风力发电技术的普及，风电在电力系统中的占比不断提高。2020年中国风电新增装机容量约为71.67 GW，成为风电新增装机规模最高的年份。到2020年底，全国风电累计并网装机容量达到280 GW以上［1-2］。大规模风电机组并网带来巨大经济效益和环境效益的同时，由于风电机组通过功率电子转换器与电网连接，转换器将风电机组旋转动能与系统分离，而风电渗透率的提高会导致系统惯量减小，系统将面临安全稳定运行的挑战［3-4］。

当电力系统发生电源侧与负荷侧不平衡的扰动后，频率将偏离标称值。由于传统的风电并网不能给系统提供惯性支撑，所以系统频率波动幅度将大幅增大。为了使系统频率能维持在安全的范围内，则需增加系统备用容量，提高系统惯量以及调频能力。文献［5-8］在机组组合决策中，满足常规静态约束的同时，还考虑了系统动态过程中的安全约束，即扰动时系统频率跌落的最低值应大于负荷侧切负荷动作的触发值。文献［9］在含有风电并网的电力系统频率响应模型的基础上，将系统动态频率约束转换成系统惯量约束，并将此约束加入机组组合模型求解。该求解方案虽满足系统频率要求，但该模型将风电机组均按照无一次调频能力处理，风电机组始终不参与系统调频，经济性欠佳。文献［10］研究了考虑风电波动的频率安全约束机组组合，并采用随机技术对风力发电行为进行准确建模。但该系统的频率动态模型存在只能适用于火电机组均为再热式汽轮机的缺陷。

近年来，国内外学者针对如何降低大规模风电并网对系统惯量以及系统频率的影响进行了大量研究，总结包括如下3种解决方法。

1）虚拟惯量控制法［11-12］，在风电机组的控制环节引入系统频率的变化信号，当频率突变时释放或吸收风电机组转子来储存动能，转换为参与调频的有功功率。文献［13］分析了虚拟惯性时间常数与风电机组转子转速以及机组出力之间的关系，并给出了风电机组虚拟惯性时间常数量化表达式。

2）超速减载与变桨距控制法［14-16］，风电机组转子超速或变桨距使其脱离最大功率输出实现减载运行，增加了风电机组有功功率储备，从而具备一次调频能力。文献［17］将风电机组超速减载备用法与虚拟惯量控制法相结合，该方法可以使风电机组具备惯性调频和一次调频能力的同时还有效地避免了风电机组转速恢复过程对系统频率的二次冲击。

3）利用电池组、抽水蓄能电站等储能系统并网以提高系统调频能力［18-19］。文献［20］讨论了如何将快速响应的电池储能器用于系统频率动态安全的维护，所提出的方法在保证频率安全性的前提下，还可以增大风电消纳能力，具有较好的经济性。

本文对风电机组采用超速减载与虚拟惯量控制，在计及动态频率约束的电力系统机组组合策略研究中考虑风电机组调频因素。当火电机组常规约束下的组合方式不满足频率限值要求时，在风电机组减载约束范围内可对风电机组进行控制，使其具备调频能力并且提高系统惯量。该策略避免了为提高系统备用容量而开启新的火电机组的情况，提高了决策的经济效益。

1 计及风电机组调频的电力系统频率响应模型

电力系统正常运行下，供电与负荷功率之间保持平衡以达到系统同步运行。但若发生突然的扰动，系统频率将经历从原先稳定状态过渡到新的稳定状态的过程。电力系统动态频率响应如附录A图A1所示，扰动发生时，系统频率经历惯性支撑与一次调频环节，于tmin时段达到频率最低值fnadir。频率最低值可反映系统动态响应过程中频率变化区间的大小，为电力系统稳定性研究提供参考标准。

1.1 风电机组调频响应

同风速下风电机组超速减载曲线与最大功率点跟踪（MPPT）曲线见图1，常规状态下风电机组运行于MPPT曲线上以追求风能利用率的最大化。

图1 同风速下风电机组超速减载与MPPT曲线Fig.1 Overspeed load shedding and MPPT curves of wind turbine with the same wind speed

由于运行在MPPT曲线上的风电机组没有可用的备用容量，所以不能参与系统的一次调频。为了使风电机组具有调频能力，本文风电机组参考文献［17］采用基于转速控制器的减载操作模式，根据不同时段风电机组一次调频容量需求，可采用不同减载量d的超速减载控制。超速法具有响应速度快的特点，但受到最大转速限制有一定的控制盲区，适用于额定风速以下的工况。根据相关资料统计，全年内风速达到及超过风电机组额定值的运行工况只占很小一部分［21］，因此，基于超速减载获取备用容量在大部分时间内均适用。本文基于额定风速以下的工况进行研究。当扰动发生时，先对运行在减载曲线上的风电机组进行虚拟惯量控制，后利用留有的备用容量对风电机组进行一次调频控制，在MPPT曲线上的点A处退出调频。

风电机组参与系统动态频率控制的过程主要分为以下2个部分。

1）惯性支撑部分

调频前风电机组运行在减载量为d的超速减载点B，输出有功功率为Pw。当系统频率发生扰动时，风电机组输出电磁功率由点B突增ΔPe到点C，为系统提供了虚拟惯性支撑。此时电磁功率大于捕获机械功率，风电机组转子将减速释放转子动能。随着转子转速逐渐降低，风电机组捕获机械功率Pw增加，电磁功率Pe逐渐减小，最终电磁功率Pe与机械功率Pw在点D达到平衡，完成风电机组虚拟惯量响应。风电机组惯性支撑效果由惯性时间常数Hw来表示，如式（1）所示。其定义为用于调频的转子动能与机组额定容量SN之比，其中风电机组参与调频的有效转子动能包含2个部分，一部分为实际机械动能的变化，另一部分为因机组转子转速变化导致的风功率捕获量变化。

式中：JD为风电机组机械转动惯量；PD为机组极对数；Pw(t)和Pw(d)分别为调频过程中t时段风电机组捕获的风功率和调频初期减载量d下风电机组捕获的风功率；ton和toff分别为惯性支撑部分开始与结束时段；ωr1(d)和ωr3(d)分别为风电机组初始转子角速度与风电机组完成虚拟惯量控制时对应的角速度，这两者均为减载量d的函数。具体参数的表达式见附录B式（B1），转子转速变化与时间的关系见式（B2）。

2）一次调频部分

由于风电机组运行在减载曲线上，可通过转子转速控制来调节风电机组的有功功率输出以补充系统频率变化的功率需求。当风电机组完成虚拟惯量控制时，系统频率偏差仍然存在，频率扰动超过死区后风电机组触发一次调频，其输出功率就会继续增加，运行状态由点D向点A移动，释放备用功率。单台风电机组参与一次调频的功率储备ΔPWdroop为最大风功率Pw0与一次调频起始风功率Pw3的差值，如式（2）所示。与常规火电机组的调速器一样，下垂控制在于提供与频率偏差成比例的输出功率。

1.2 计及风电机组调频的电网频率响应模型

当系统发电量损失后，频率开始以一定的衰减速率下降，电力系统动态频率响应由摆动方程得出：

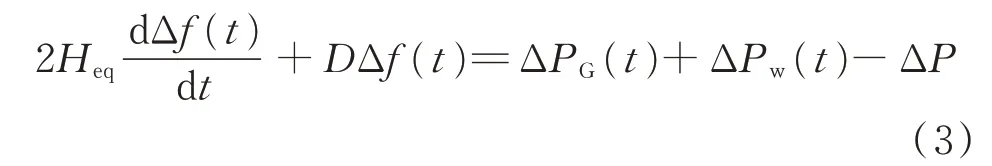
式中：Δf（t）为频率偏差；D为负载阻尼系数；ΔPG（t）和ΔPw(t)分别为在发电量损失ΔP下，火电机组和风电机组输出功率的增加量；Heq为虚拟惯量控制下风电机组并网的系统总惯性时间常数。

已有文献对传统动态频率响应模型及调速器建模进行了研究。文献［22］在文献［23］的基础上介绍了一种通用的频率响应模型，该模型能够表示每个调速器对系统频率控制的作用。本文在文献［22］中的动态频率响应模型的基础上添加了风电机组一次调频与惯性响应部分。

将式（3）进行Laplace变换，可以分为系统惯性响应部分G1(s)、式（3）中等号右侧前2项对应火电机组一次调频部分G2(s)和风电机组一次调频部分G3(s)。以系统发电量损失ΔP为输入，频率偏差Δf为输出进行建模，形成计及风电机组调频的多机系统频率响应模型，如图2所示，该模型可反映机组惯性支撑与一次调频响应过程。

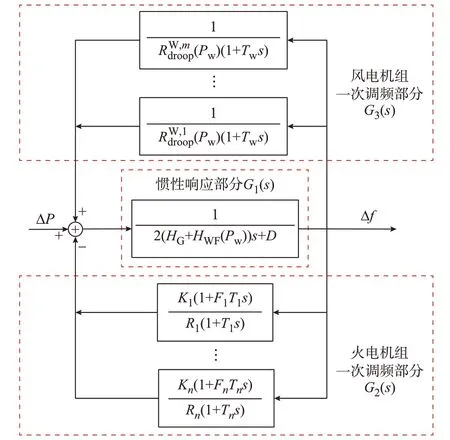
图2 含风电机组调频的系统频率响应模型Fig.2 Frequency response model of system with frequency modulation of wind turbine

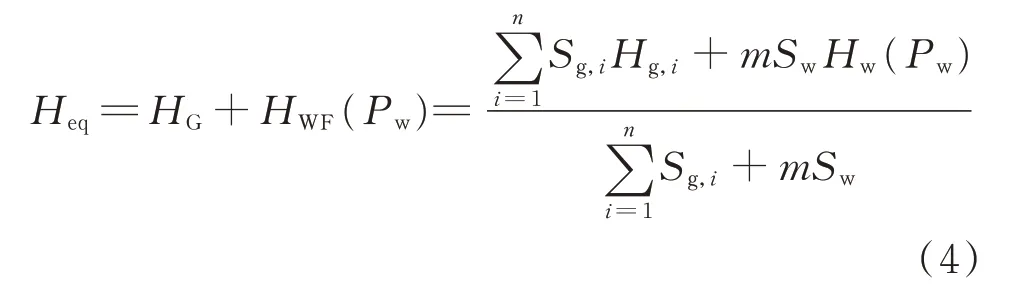
式中：HG为火电机组总惯性时间常数；Sg，i和Hg，i分别为第i台火电机组的容量和惯性时间常数；Sw为单台风电机组的容量。

由1.1节分析可知，风电机组静态调差系数可由式（2）表示为以风功率为变量的函数RWdroop(Pw)，故图2中风电机组一次调频部分等效为一阶惯性环节后其频域的表达式，即

则图2中的传递函数可表示为：

研究表明，由于不同调速器的时间常数Ti与Tw在其允许范围内对系统频率下降影响很小，所以式（6）中所有机组调速器的时间常数可都由相同的值TR替代［23］。将式（6）简化后得到系统频率偏差Δf的频域表达式为：

式中：ωf为固有振动频率；ξ为阻尼比。

将式（7）进行Laplace反变换，可得系统频率偏差Δf（t）的时域表达式。为得到频率最低值，将Δf(t)的时域表达式对t求导，可知在频率最低点处dΔf(t)/dt＝0。在功率缺额和负荷调频系数确定的情况下，系统频率最低点可表示为：

式中：f0为基准频率；tnadir为最低点频率对应时间。

频率最低点反映了扰动下系统稳定性的边界情况，为了进一步研究频率最低值fnadir与Heq和RT之间的关系，可将式（9）中变量之间的变化关系由附录A图A2表示，此时负荷功率Pload＝250 MW，ΔP＝25 MW，D＝1。当系统单位调节功率RT与惯性常数Heq变化时频率最低值fnadir的变化情况见图A2（a）。将图A2（a）中曲线分别投影至RT-fnadir平面与Heq-fnadir平面，如图A2（b）和（c）所示。分析可知，fnadir随Heq和RT增大而增大，所以提高系统惯性水平与调频能力对频率的安全稳定有积极作用。风电机组参与系统调频可以降低传统电力系统对惯性和一次调频的要求，提高了系统单位调节功率和惯性水平从而提升了系统动态频率稳定性。

2 机组组合

2.1 机组组合目标函数

机组组合的目的是寻找系统中的发电机组最佳调度，以最大限度地降低运营成本并同时满足系统运行限制。本文的目标函数分为4个部分：火电机组发电成本、机组启停成本、风电机组运维成本及风电机组超速减载产生的经济损失［19］。机组组合的目标是将各时间段总运营成本降至最低，则目标函数可表示为：

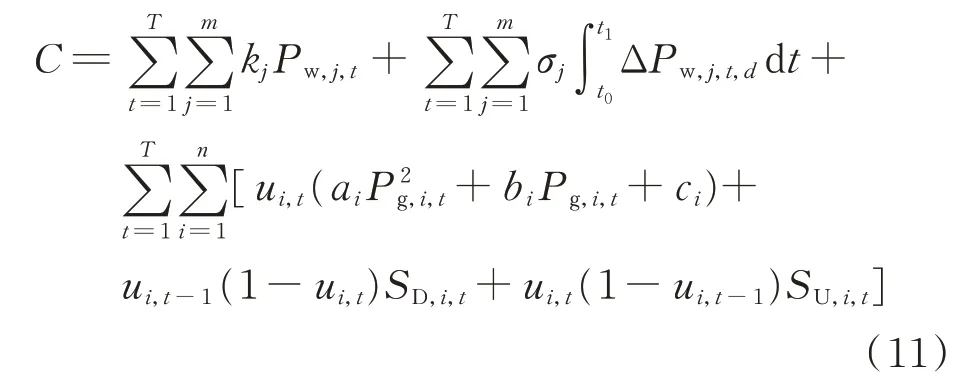
式中：T为调度周期小时数；kj为第j台风电机组运维成本系数；ai、bi和ci为第i台火电机组发电成本系数；ui，t为t时段第i台火电机组启停状态，取值为1表示开启，为0表示关闭；Pg，i，t与Pw，j，t分别为t时段第i台火电机组与第j台风电机组的输出功率；SD，i，t和SU，i，t分别为启、停成本；σj为第j台风电机组的超速减载成本系数；ΔPw，j，t，d为t时段第j台风电机组在减载量d下的功率损失；t0和t1分别为机组组合单位时段的起始和终止时段。

2.2 机组组合常规约束

1）功率平衡约束

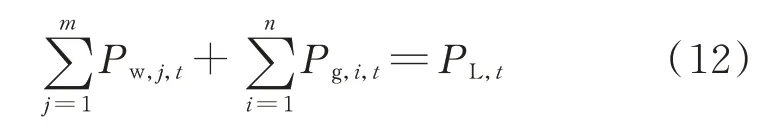
式中：PL，t为t时段的计划负荷。

2）火电机组常规约束

式中：ωr为转子转速；ωr，min和ωr，max分别为ωr的最小值和最大值；Pw，j，t，max为Pw，j，t的最大值。

式（18）和式（19）分别为转子转速约束和功率约束。

4）系统旋转备用约束

式（15）—式（17）分别为火电机组出力约束、爬坡约束和启停约束。

3）风电机组常规约束

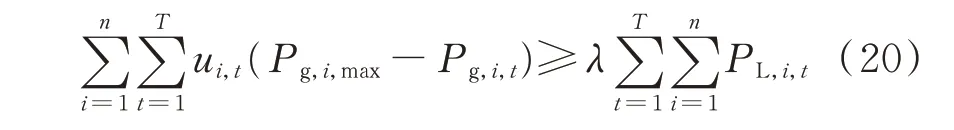
式中：λ为备用系数；PL，i，t为t时段第i台火电机组的计划负荷。

2.3 频率动态约束建模

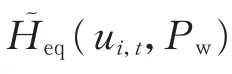
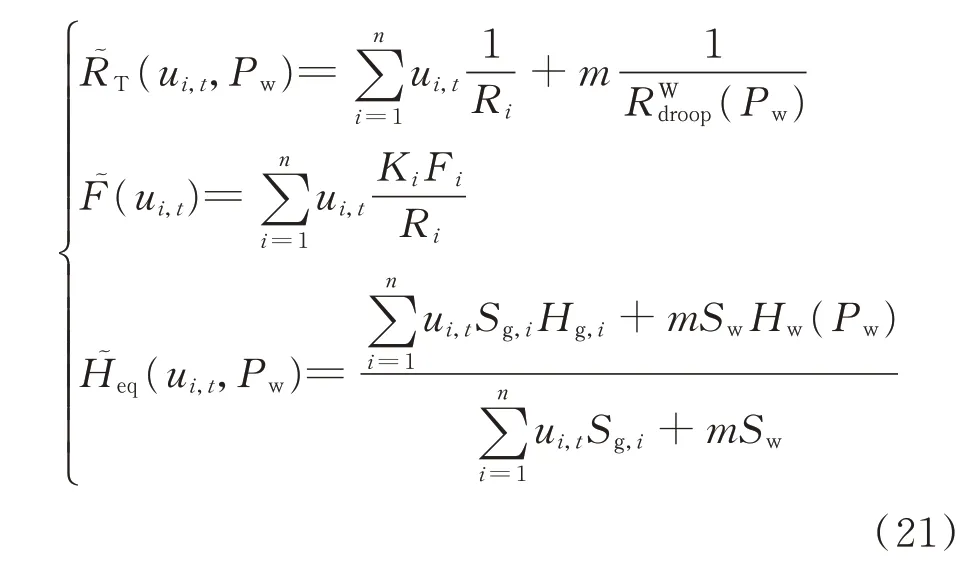
式中：“～”表示对应变量考虑开关决策的形式。

将含开关策略的参数代入式（9）使频率最低值大于限值，即得频率约束。

式中：fmin为频率限值。

由于频率约束式（22）具有高度非线性的特性，求解混合整数非线性规划问题会对求解器带来较大的负担，所以采用多元分段线性化技术对式（22）进行线性化处理。

为了提高计算效率，本文采取Benders分解法将优化问题分为1层优化和2层优化。1层优化由常规约束组成，2层优化为频率越限检测。为了检验频率是否满足要求，在2层优化中引入惩罚变量ψt，将频率最低点越限问题转化为惩罚变量最小化问题，则式（25）被改写为：

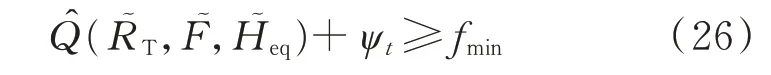
通过2层优化可以计算得到ψt，若某时段惩罚变量大于0，则说明在该时段1层优化解得的机组组合方案存在频率最低值越限的问题，此时将1层优化结果传递到Benders反馈约束，约束表达式如下。

2.4 算法流程

本文提出的风电机组参与调频的含频率动态约束机组组合模型的求解过程主要分为分层优化和迭代修正2个部分，具体流程见图3，具体步骤如下。

图3 机组组合模型求解流程图Fig.3 Flow chart of unit commitment model solution

步骤1：运用拉格朗日松弛算法进行求解以满足1层优化中常规约束条件式（12）—式（20）的要求，得到的组合结果传递到2层优化求解惩罚变量ψt。

步骤2：判断惩罚变量ψt是否小于0。若ψt小于0，则组合结果符合频率限值要求，输出该时段组合方案；若ψt大于0，则进入Benders割求解，增加约束条件式（27），得出结果返回1层优化，依次循环至惩罚变量ψt满足要求后输出组合结果。

3 算例分析

为验证本文所提出的风电机组参与调频的含频率约束机组组合模型可改善系统动态频率，使用MATLAB软件平台结合CPLEX12.1求解器对含风电并网的10机系统进行机组组合优化计算。算例系统中火电机组运行特性参数见附录B表B1，火电机组动态参数见表B2，阻尼系数D＝1，TR＝8 s［24］。系统风电场由500台装机容量为1.5 MW的风电机组组成，风电渗透率为31%，风电机组参数与文献［25］一致。调度周期为24 h，24 h内负荷曲线以及风电最大出力曲线如附录A图A3所示。算例系统基频为50 Hz，安全频率限值为49.2 Hz，假设扰动为系统突增10%的负荷。

采取以下3种机组组合方案，并将结果进行比较。

方案1：含常规约束式（12）—式（20），不含系统频率约束的机组组合方案，结果记为H1。

方案2：在方案1的基础上增加系统频率约束式（26），但风电机组不提供惯性支撑与一次调频，仅由火电机组参与系统调频。即式（6）中HWF与G2（s）部分均为0，结果记为H2。

方案3：在方案1的基础上增加系统频率约束式（26），其中风电机组参与调频，结果记为H3。

表1记录了24个时段（1 h为1个时段）扰动发生时频率偏差的最大值。表2记录了方案3下各时段风电机组减载情况。机组组合目标函数中计及了每台火电机组各时段下的出力大小，在模型的常规约束条件与系统频率动态约束条件中对火电机组出力取值范围进行了约束，通过对优化模型目标函数的求解计算可确定各时段下火电机组的出力大小。3种方案下各时段火电机组出力大小见附录A图A4。

表1 24 h内最大频率偏差Table 1 Maximum frequency deviation within 24 hours

选取一日内负荷最小与最大时段（时段1和时段12）为例。对于时段1，方案1仅开启火电机组U1提供负荷需求，系统惯性系数较小导致系统频率稳定性较差。当系统负荷突增10%时，该方案频率跌落的最低值为49.09 Hz，低于频率安全范围。同一时段下，方案2选择开启火电机组U2、U3、U4，相较于方案1，该方案通过增加火电机组开启数量提高系统备用容量，从而提高了系统调频能力。相同扰动下，频率跌落的最低值为49.28 Hz，满足频率安全要求。方案3采用风电机组减载方式使风电机组具有调频能力。在时段1下具备足够的风能，由表2可知，该时段对风电机组进行减载9.90%操作，风电机组参与系统惯性支撑和一次调频，配合火电机组U1可使系统具备足够调频能力，方案3下频率跌落最低值为49.20 Hz，满足频率安全要求。

表2 方案3中24 h内风电机组减载量Table 2 Wind turbine deload within 24 hours in scheme 3

在时段12扰动发生时，3种运行方案对应的系统频率动态响应见附录A图A5。由于负荷增加，方案1下火电机组U5处于开机状态，扰动发生后3.56 s，该方案达到的系统频率最低值为49.10 Hz，该方案下不符合频率最低值要求。相较于方案1，方案2增开火电机组U6和U7，增加备用容量以抵抗干扰对频率的影响，该方案下，扰动发生后3.32 s，系统的频率达到最低值49.28 Hz，符合频率最低值要求。结合附录A图A6中3种方案下扰动发生时单台风电机组输出功率变化曲线可知，方案1和方案2中风电机组均未采取控制措施，扰动发生时风电机组依旧运行于MPPT曲线，功率输出不变。方案3相较于方案1多开启一台火电机组U6，其余由风电机组进行减载9.65%以增加备用容量，增大了系统惯量与一次调频能力。该方案下在风电机组扰动初期，由于虚拟惯量控制输出功率突增，随着转速和频率偏差减小，输出功率的增幅逐渐减小，最终降至MPPT功率并保持稳定。扰动发生后3.47 s，系统的频率达到最低值为49.20 Hz，满足频率最低值要求。将3种方案的火电机组运行容量进行对比，方案1中火电机组运行容量为1 332 MW，方案2中火电机组运行容量为1 497 MW，方案3中火电机组运行容量为1 417 MW，方案3相较于方案2少启动一台机组，火电机组运行容量减小，节约了发电成本。

图4为3种方案下24个时段频率最低值的分布图，结合图5各时段风电出力曲线可得：虽然方案1中风电机组处于最大出力状态，但是由于风电机组不参与系统调频，且风电出力占比较高，扰动发生时该方案频率最低值在49.16±0.11 Hz范围内波动。

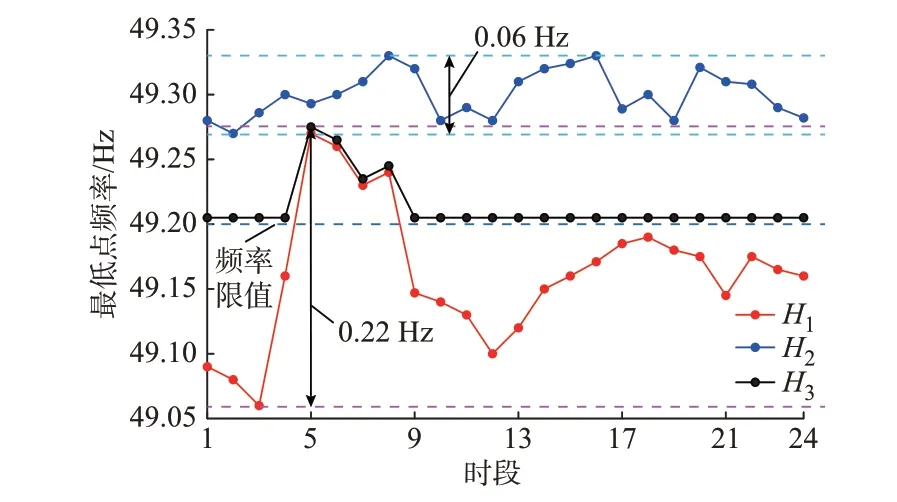
图4 频率最低点分布Fig.4 Distribution of lowest frequency point

图5 风电出力曲线Fig.5 Output curves of wind power

24个时段中仅有时段5至时段8满足频率要求，其余时段系统频率均明显低于频率限值，系统频率稳定性差，该方案不能满足系统频率约束要求。方案2考虑系统频率动态约束，但风电机组不参与调频，该方案系统通过增加火电机组启动数目来提升系统惯量以及备用容量。此方案下频率最低值在49.30±0.03 Hz范围内波动，各时段均满足频率约束要求，有较好的系统频率稳定性。但是，该方案由于火电机组出力的增加，风电出力大幅减少，风电利用率下降严重。方案3考虑了计及风电机组调频的系统频率动态约束。该方案利用风电机组减载调频，将各时段频率最低值控制在49.20 Hz以上，均满足系统频率要求。其中，时段5至时段8由于火电机组调频能力已满足要求，所以该时段风电机组不采取减载调频动作，与方案1相同，时段5至时段8的风电机组处于最大出力状态。方案3与方案1相比，风电机组虽然不是处于最大出力状态，但是该方案提高了系统频率稳定性。方案3与方案2相比，2种方案均满足系统频率稳定性要求，但方案3的风电出力占比明显高于方案2，风电出力最高可提升23.29%。方案3满足系统频率动态约束的同时还提高了系统风电消纳能力。

为进一步验证风电机组参与调频的机组组合方案与传统机组组合方案相比的优越性。将24个时段内3种方案下火电机组开机台数进行统计，如附录A图A7所示。在满足系统频率动态约束的前提下，方案3的火电机组开启台数明显少于方案2，减少火电机组开启，增加了燃煤经济性。结合附录A图A4中3种方案下火电机组出力大小可见，方案3的火电机组各时段出力总和小于方案2，方案3下系统具有更好的风电消纳能力。

3种方案的发电成本分别为543 307、561 032、554 216美元，将3种方案成本进行对比可得：方案2和3与较方案1相比，由于增加系统动态频率约束，2种方案的发电成本均有所增加。但方案3相较于方案2的发电成本有所减少。在满足频率动态约束要求的情况下，方案3的经济性要优于方案2。