基于DOE算法的涡旋压缩机曲轴支承跨距优化及动态性能研究*

叶 畅,季进军,胡 波,相玲玲

(1.江苏电子信息职业学院 数字装备学院,江苏 淮安 223003;2.江苏电子产品装备制造工程技术研究开发中心,江苏 淮安 223003;3.广州万宝集团有限公司,广东 广州 510130)

0 引 言

对于涡旋压缩机而言,曲轴是其最重要的驱动装置,曲轴的性能会对涡旋盘的质量造成影响,导致其啮合容易损坏[1],并且会使压缩机寿命缩短。对于曲轴部件来说,在众多的影响因素之中，支撑跨距是相对比较重要的一个影响因素[2]。在曲轴零件的设计中,关键问题是选择合理的支承跨度[3]。如果支撑跨距选择不当,在交变气体力作用下会引起曲轴偏心段的大位移,从而引起涡旋压缩机的振动和磨损,更会增加滚动头的磨损和轴承中滚动体、内外环及支承件的磨损,从而大大缩短压缩机的使用寿命[4]。

不管是在国内还是国外,对于曲轴优化设计领域的研究以及动态性能领域的研究都相对较少。刘涛[5]根据涡旋压缩机的动力学模型,建立了曲轴的有限元模型,通过软件分析获取了前6阶振型,分析了不同情况的振型差异,为优化设计提供了依据。胡萍[6]利用数学模型的方式,对模型进行了研究,具体地分析了曲轴的相关特性,对设计曲轴有很大的帮助。余洋[7]建立了主轴多刚体模型,通过动力学分析,得到了壳体在气体载荷下承载来自于曲轴的载荷,为减轻壳体载荷优化曲轴设计提供了依据。刘袁帅[8]分析并研究了涡旋压缩机运转时其曲轴部件在力学方面的一些特性,然后利用原本的设计方式进一步地优化了曲轴的相关参数,对于优化曲轴而言具有很大的价值。

以上研究都是针对曲轴-轴承系统进行数学建模、有限元分析,没有针对曲轴支撑跨距这一关键曲轴参数的细分研究。

本文通过DOE算法优化曲轴跨距以及曲轴轴长的相关参数,进而通过数学模型的方式分析方案当中曲轴以及曲轴部件的相关参数,最后对应力以及位移的变化情况进行总结。

1 曲轴最优跨距的理论计算

曲轴的受力结构图如图1所示。

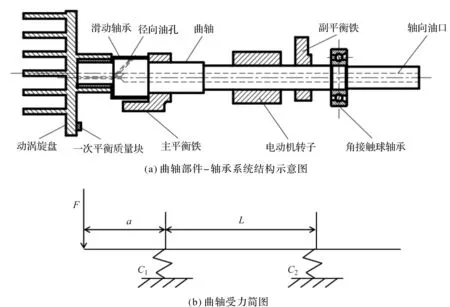
图1 曲轴受力结构图

笔者以曲轴径向刚度K为指标,探究支承跨距对曲轴径向刚度的影响[9]。

曲轴的径向刚度为:

(1)

式中:K—曲轴径向刚度,N/mm;F—径向气体力,N;y—曲轴偏心部位处位移上限,mm。

其中:

(2)

将其代入可得:

(3)

式中:a—曲轴偏心段长度,mm;E—弹性模量,MPa;C1,C2—曲轴前、后轴承的支承刚度;l—曲轴跨距,mm;Ia—曲轴偏心段部分的惯性矩;Il—曲轴跨距部分的惯性矩。

1.1 传统设计方法

曲轴偏心段前端受径向气体力F作用时引起的总位移y包括以下几个组成部分:

(1)曲轴剪切变形所引起的径向位移;

(2)曲轴弯曲变形所引起的径向位移;

(3)因上轴承所对应的弹性发生改变而导致的径向位移。

最优跨距的计算公式为[10,11]:

(4)

式中:E—弹性模量,N/m2;Dl—曲轴跨距所对应的直径平均值,mm;dl—曲轴跨距所对应的孔径平均值,mm。

在曲轴最优跨距的具体设计时,通常由于自身结构的限制会导致实际跨距l≠lo,这会引起曲轴部件刚度的损失。如果0.75≤l/lo≤1.5,对于曲轴部件而言其刚度会损失掉5%,而损失程度不会高于10%,所以轴承支承跨距处于该区间中的话,就是相对合理的,这也被叫做合理跨距lrat,也就是lrat=(0.75～1.5)lo。

经过计算,求得合理支承跨距的范围lrat=121.5 mm～243 mm。

1.2 卡丹公式设计方法

曲轴偏心段在受气体力F的作用下产生位移为y,并令dy/dl=0,则Dl-dl=0由式(4)得:

(5)

通过卡丹公式对式(5)进行解答,在得出的所有结果里存在复数域根、共轭复数根以及正根。因为在实际过程中跨距是实数,在得出的结果中只有一个解,那就是正的实数根。

根据本文所选定的曲轴的参数得:lo≈223 mm。

通过以上两种方法的联合设计,可得出相对准确的最佳跨距数值。

2 DOE优化分析

文献[12]证明了真正影响曲轴静动态性能的是垂直于曲轴轴线方向的切向气体力,而在该过程中出现的法向气体力相对比较小,通常不进行计算。文献[13]对涡旋盘进行排气时所出现的切向气体力的计算给出了详细的计算方法,根据该方法进行计算,能够得出F=777.5 N。

在静态性能分析后得到曲轴原始应力和变形数据为:总位移变形为42.628 μm,x轴方向最大形变量为42 μm,所受到的最大应力值为36.5 MPa,通过一系列运算最终了解到,曲轴x轴上所对应的静刚度是28.55 N/μm。

曲轴结构图如图2所示。

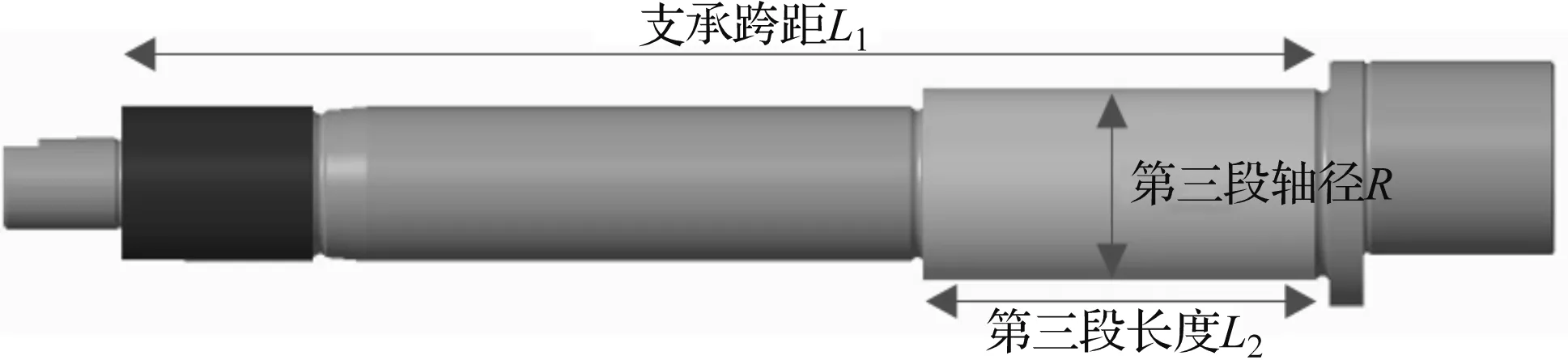
图2 曲轴结构示意图

通过DOE算法计算曲轴轴承的相关参数,并对其进行一定的优化设计。在图2中能够看出支承的跨距L1以及曲轴的第三段中轴径R与长度L2优化的具体情况,以此来促使曲轴应力以及出现的形变量尽可能地减弱,进而强化曲轴的刚度。对曲轴轴承的相关性能进行具体的分析与研究,设置形变量的数值0.042 628 mm,通过计算能够得出曲轴的最大应力应该为68.8 MPa。

曲轴强度校核计算公式:

(6)

式中:Sσ—只考虑弯矩时的安全系数;σs—曲轴材料的屈服强度极限;σmax—曲轴偏心段根部危险部位的最大应力值。

通过对上述运算进行分析,能够获得曲轴被完善之后所对应的数学模型,具体为:

135 mm≤L1≤149 mm;16.5 mm≤R≤21 mm;42 mm≤L2≤62 mm;形变量最大值Smax≤0.042 628 mm;最大应力P≤68.8 MPa。

为了研究曲轴的跨距、曲轴第三段轴径和长度对应力集中和位移变形的影响,通过同时优化不同的跨距、曲轴第三段轴径和长度数值,确定最为合理的设计使得曲轴静刚度最大,所受的应力最小。具体的分析结果如表1所示。

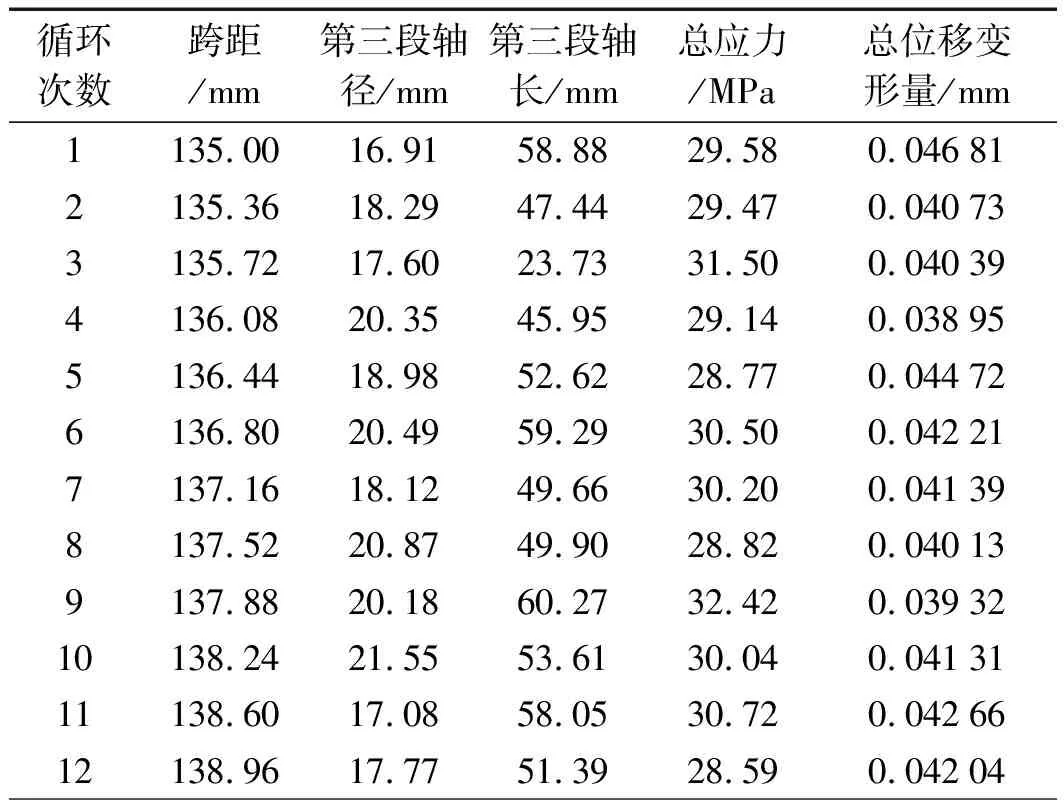
表1 DOE分析结果

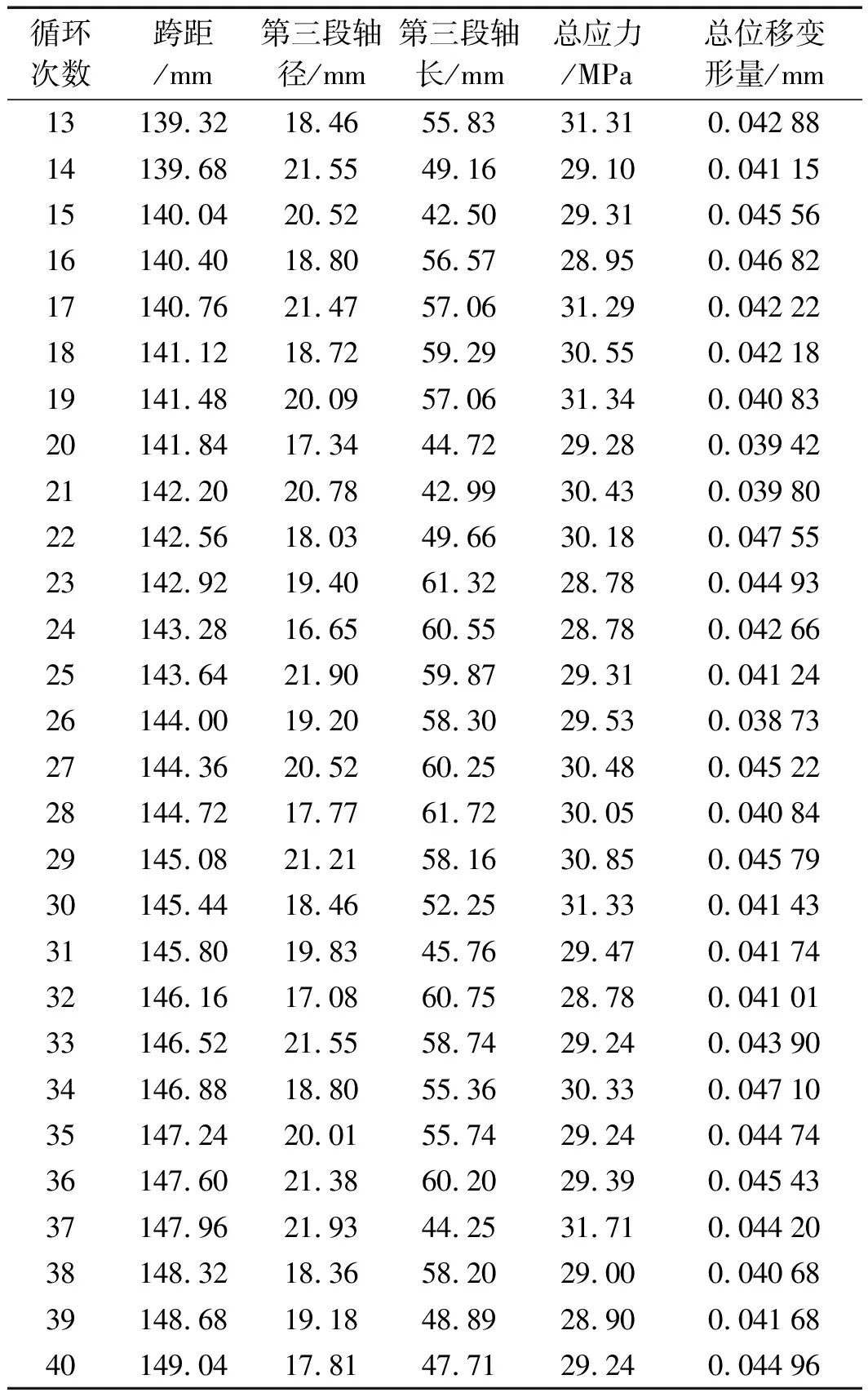
(续表)

根据表1能够看出优化的具体数据,如果曲轴跨距L1为144 mm,而且轴径R为19.2 mm,轴长L2为58.3 mm,该过程中所产生的形变量最不明显,最低值为38.73 μm。而此时的应力是29.53 MPa,与最大值比较,曲轴所受的应力减小了8.9%,静刚度提高了约18.5%。

3 有限元模态分析

笔者利用优化之后的一系列参数建立数学模型[14],将曲轴和曲轴部件作为主体,研究曲轴受力的具体情况,并计算相关数据。通过有限元分析方式,研究并分析曲轴以及曲轴部件的振型分布规律。

对于有限元模态分析,振动频率ωi和模态φi由下面的方程[15,16]计算得出:

([K]-ωi[M]){φi}=0

(7)

式中:[k]—刚度矩阵;[M]—质量矩阵。

此处利用有限元分析的方式[17,18]主要是为了深入了解到模态的相关参数。

曲轴以及相关组件在材料学方面所呈现出来的特性详情如表2所示。

曲轴和曲轴部件有限元分析结果的对比如表3所示。

曲轴所对应的振型如图3所示。

曲轴部件所对应的振型如图4所示。

根据模态分析能够看出:对于曲轴部件而言,其频率相对曲轴低。在第1阶中曲轴与曲轴部件的频率分别是2 059.2 Hz和384.95 Hz,从中能够看出曲轴的频率要比曲轴部件的频率高81%左右。由此能够表明,所有的零件装配以后会使得其动态特性明显降低,非常容易在电机与涡旋盘产生摩擦的情况下发生一定的共振现象,出现共振主要是由于曲轴与转子对其平衡产生的影响。

表2 曲轴以及相关组件在材料力学方面的特性

表3 曲轴和曲轴部件各阶固有频率有限元分析结果对比

图3 曲轴前6阶固有振型

图4 曲轴部件前6阶固有振型

在涡旋压缩机中的零部件电机，其工作状态下的转速从1 800 r/min到5 400 r/min,频率从30 Hz到90 Hz,频率和曲轴部件相比较低,曲轴部件在工作的状态下能够很好地避免出现共振,使得工作相对安全。

4 曲轴及其部件谐响应分析

将曲轴偏心段在静态分析中所受到的气体切向力最大值作为简谐载荷的幅值,加载在曲轴偏心段的中心截面上。根据曲轴和曲轴部件模态分析所得到的固有频率值,设置曲轴所受简谐载荷的频率值范围为2 009 Hz～10 550 Hz;设置曲轴部件所受到简谐载荷的频率值范围为350 Hz～3 050 Hz。

曲轴位移随频率变化的响应图如图5所示。

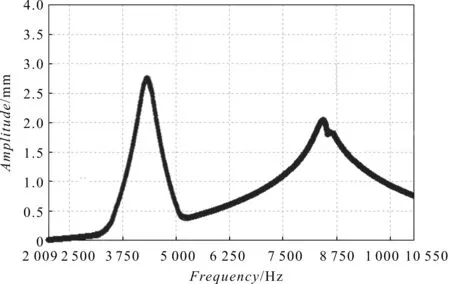
图5 曲轴位移随频率变化的响应图

曲轴部件位移随频率变化的响应图如图6所示。

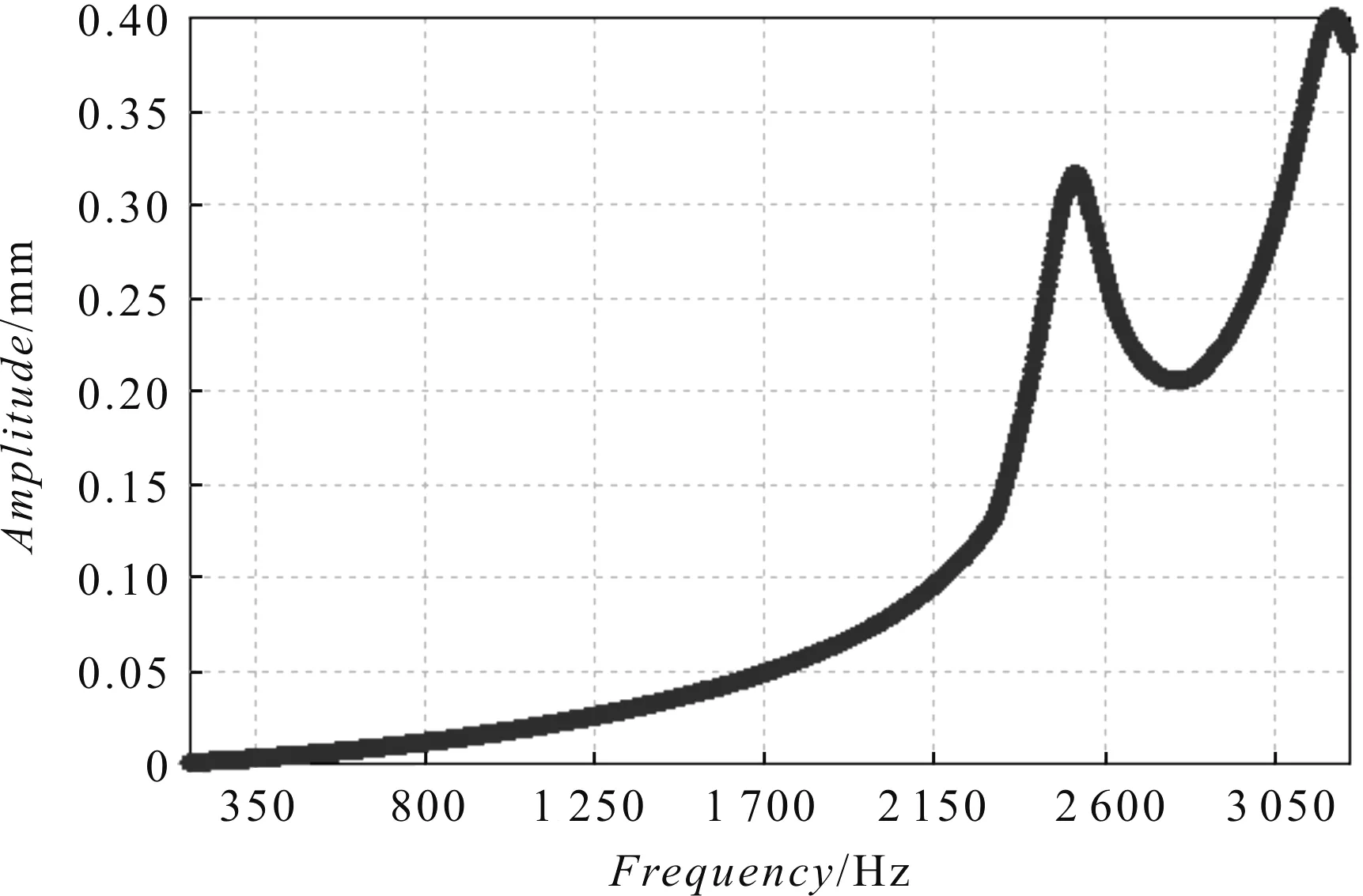
图6 曲轴部件位移随频率变化的响应图

从图5和图6中能够看出,当曲轴的频率处于3 000 Hz到5 200 Hz之间时,位移会出现较大的变化;图5中，当处于4 242 Hz时，位移会到达顶峰,峰值是2.854 mm。图6中，对于曲轴部件而言,其峰值出现在3 150 Hz时,峰值是0.4 mm。曲轴部件位移变化最大值较曲轴位移变化最大值减小了86%。通过曲轴和曲轴部件两种结构下谐响应分析可知,曲轴部件的位移随频率的最大值远小于曲轴的位移,因此,曲轴、轴承位置及设计满足要求。

5 实验验证

笔者将设计的主轴及主轴部件装在样机上,并置于噪音振动试验台进行了装机验证;将其与目前市场上主流产品谷轮型号ZF08KQE-TFD、日立型号NS300DHV-47D2G等同类产品进行数据对比。

噪音振动试验台如图7所示。

图7 噪音振动试验台

对比噪音振动频谱图如表4所示。

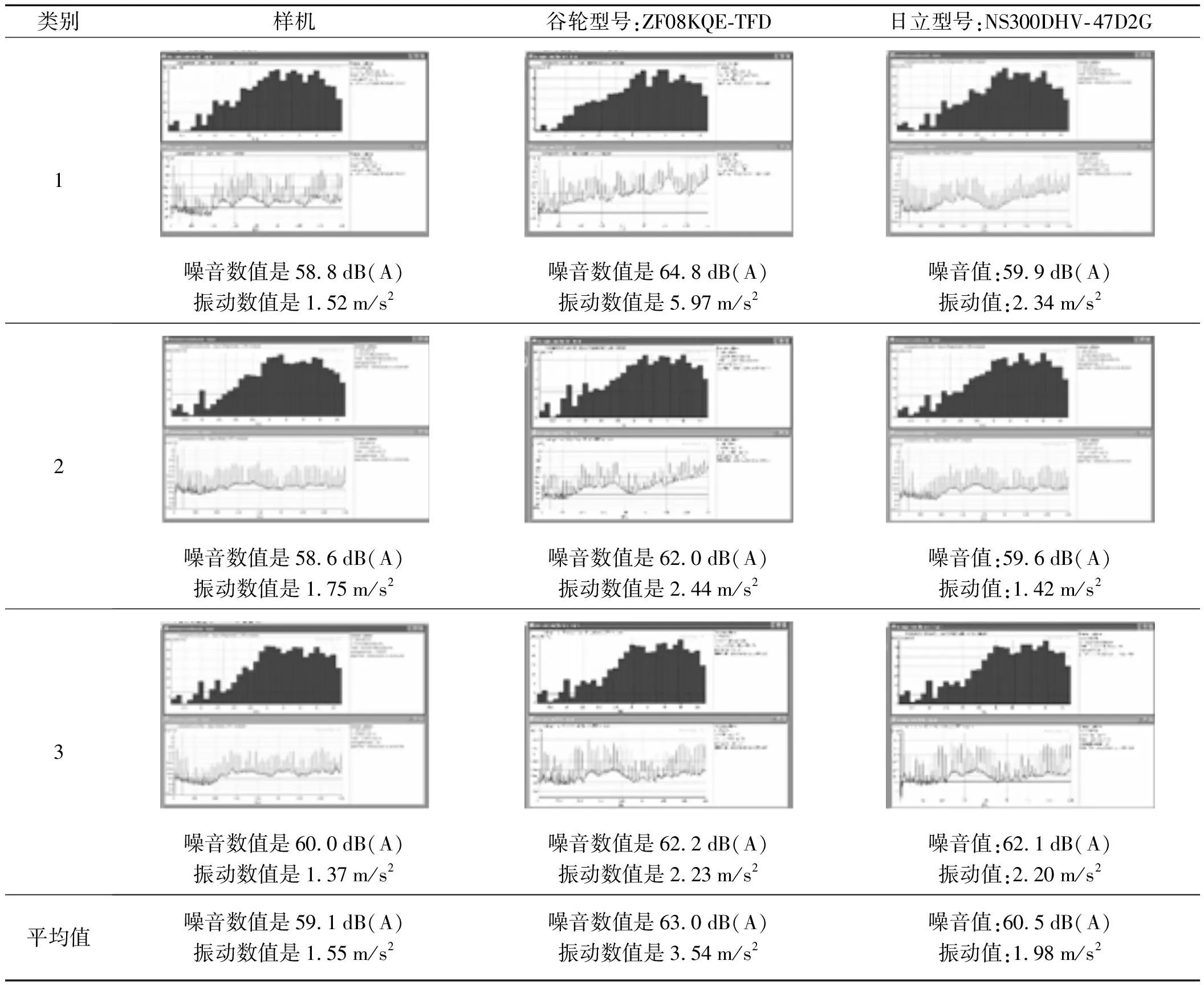
表4 压缩机噪音/振动测试数据

从表4中看出:对比同类产品,压缩机的噪音值至少下降1.4 dB(A),振动值至少下降0.43 m/s2;在各频率，噪音振动均未出现异常,噪音振动平稳,波动小。

6 结束语

对于涡旋压缩机而言,支承跨距是影响曲轴性能和寿命的关键要素,笔者通过DOE算法优化了曲轴跨距以及曲轴轴长的相关参数,并进行了数据仿真分析和实证实验,其研究结果为曲轴系统的优化设计提供了参考。

研究结论如下:

(1)采用传统设计和卡丹公式设计两种方法对曲轴的支承跨距进行了设计,进而通过DOE优化算法对曲轴跨距和轴长进行了多参数优化;优化方案中，曲轴的位移变形减小了18.5%,曲轴所对应的静刚度大幅提升;所承受的应力降低了8.9%,运动模式更为理想;

(2)对曲轴以及相关组件展开了模态研究,在此基础上获得了前6阶固有频率、振型和对应的特征属性,确保在现实激振频率下不会轻易产生共振现象;并以此为前提针对曲轴以及相关组件的各个位置进行了谐响应研究,从而获得了在频率发生改变时,应力以及位移的所呈现出来的特征属性;曲轴以及相关组件的模态完美避开共振位置,曲轴以及轴承接触面应力在较大程度上低于零件材料强度以及疲劳上限值;

(3)通过实验与同类产品对比,压缩机噪音值至少下降了1.4 dB(A),振动值至少下降了0.43 m/s2,在各频率噪音振动均未出现异常,噪音振动平稳,波动小。

当前涡旋压缩机涡旋齿通常存在吸气过热、低绝热效率、难以提高压缩比等方面的问题。为此,在后续的研究中,笔者将针对这些问题,展开关于涡旋齿型线方面的创新研究,以解决现有的技术难题,并更好地兼顾内容积比和齿端强度。