表面等离子体激元在圆筒形金属波导中的角动量特性
2021-08-23郭健宏
王 鑫,高 琪,郭健宏
(首都师范大学物理系,北京 100048)
0 引 言
表面等离子体激元(surface plasmon polariton,SPP)是局域在金属表面的一种由自由电子和光子相互作用形成的混合激发态[1-3].在这种相互作用中,自由电子在与其共振频率相同的光波照射下,发生集体振荡.这种表面电荷振荡与光波电磁场之间的相互作用构成了具有独特性质的SPP.与自然光的传播不同,SPP波的自旋并非与传播方向一致(或相反),而是具有与传播方向保持垂直方向的分量,这种现象被称为反常自旋.近几年的研究表明,利用SPP携带自旋信息的不对称性,可以通过控制入射光的自旋方向,使得SPP向不同轨道方向进行传播,这种现象被称作光子自旋霍尔效应(photonic spin Hall effect,PSHE)[4].这在 光学集成信息处理和量子光学技术方面具有很大的应用潜力[5-6].
极化激元的概念由固体物理学家黄昆于20世纪50年代提出[7].1965年,导体磷化镓的拉曼散射实验证实了极化激元的存在[8],随后,证实其他材料也能产生极化激元.1998年,Ebbesen等[9]用 SPP解释了金属亚波长结构的电磁波反常透射,SPP引起了更广泛的关注.21世纪初,随着研究的深入,人们开始关注不同结构上表面等离子体激元的能带及传播性质[10-13].伴随量子自旋霍尔效应在实验中被观察到[14],Onoda等[15]从理论上明确提出,光子体系应存在与电子体系类似的自旋霍尔效应.2008年,Hosten和Kwait[16]在实验中观测到了光子系统中的自旋霍尔效应.同年,Bliokh 等[17]证实,将光掠入射到一根圆柱形玻璃介质中,圆柱形的介面使光沿螺旋形轨迹传播,从而不断改变光子的自旋角动量,并导致自旋-轨道角动量耦合,进而产生类似的光束分裂.2015年,Bliokh等[4]阐述了在真空-金属界面的SPP表现出固有的量子自旋霍尔效应,具有自旋动量锁定的模式,并把这称之为光的量子自旋霍尔效应.
然而,大多数关于SPP的自旋霍尔效应的研究都是在平面金属上实现的,若能在线型材料上实现PSHE[18],将更有利于光子线路中的应用.目前,对于圆柱形材料,尤其是圆筒形的研究较少,基于这种考虑,本文对圆筒形金属波导中实现PSHE更有兴趣.这项工作将涉及许多理论问题,其中最基本的问题,首先要解决金属圆筒波导中电磁波本征模携带角动量的问题.虽然已经解出了其中的本征模[19],但对其角动量,特别是自旋角动量,还没有全面清楚地了解.本文拟通过推导得到圆筒形波导中光子平均自旋的解析公式,并在寻找圆筒形波导中光子自旋方向的手征特性.
1 圆筒形金属波导中的SPP本征模和场分布
本文研究的波导为圆筒形金属(图1),其内外半径分别是r1和r2,以圆筒轴向为z方向建立柱坐标系,图中Ⅰ、Ⅱ和Ⅲ3个区域分别表示圆筒的内芯、金属包层和外界环境.

图1 圆筒形金属波导结构
圆筒形金属波导结构中的本征模可表示为[19-20]:

式中E为电场强度,H为磁场强度,μ为相对磁导率,ε为相对介电常数,c为光速,ω为SPP的角频率,j表示环境中的不同区域,即图1中的Ⅰ、Ⅱ和Ⅲ区和分别是2类修正贝塞尔函数In和Kn的线性组合,满足:

kz为波矢k⇀的z方向分量,kj为r分量,二者满足

由于方程(1)中包含修正贝塞尔函数,是一个超越方程,没有解析解,只有在选取合适的圆柱尺寸的情况下,带入给定的ω,得到kz的数值解.本文选择r1和r2分别为85和90 nm的银金属管为例,计算在ε1和ε3均为10的电介质环境下,光子能量为2.1 eV的SPP的本征模.其1~3阶模的系数解如表1所示(注:未给出参数均为0).

表1 SPP 1~3阶模的场量系数及波矢
为了解角动量特性,需要将本征模的电磁场分布表示出来.对于圆筒而言,其横截面上的电场分布是整体旋转的[21],其旋转方向由角量子数(n)决定,其携带的轨道角动量为nℏ[22],n同时也是本征模的阶数.这些基本特征都是由表达式为A(kz,kjr)ei(nθ+kzz-wt)的形式解构造出来.
本文研究纵向剖面上的电场分布.柱坐标系中θ=0截面上的电场投影如图2所示.通过分析可知,柱坐标系中SPP截面上的电场具有如下特征:(1)内外电场的模相差不大,沿z方向没有明显的变化,变化的只是电场方向;(2)电场方向沿z方向有周期性变化,内外表面周期相同,但内外表面的电场方向呈镜像对称分布;(3)经过1/4周期,内外表面电场分布整体向右移动,说明SPP向z的正方向传播;(4)经过1/4周期,在同一位置电场方向发生了旋转,外表面逆时针旋转,内表面顺时针旋转.以上特征说明,因为电场在旋转,圆筒形波导中的SPP也携带自旋.
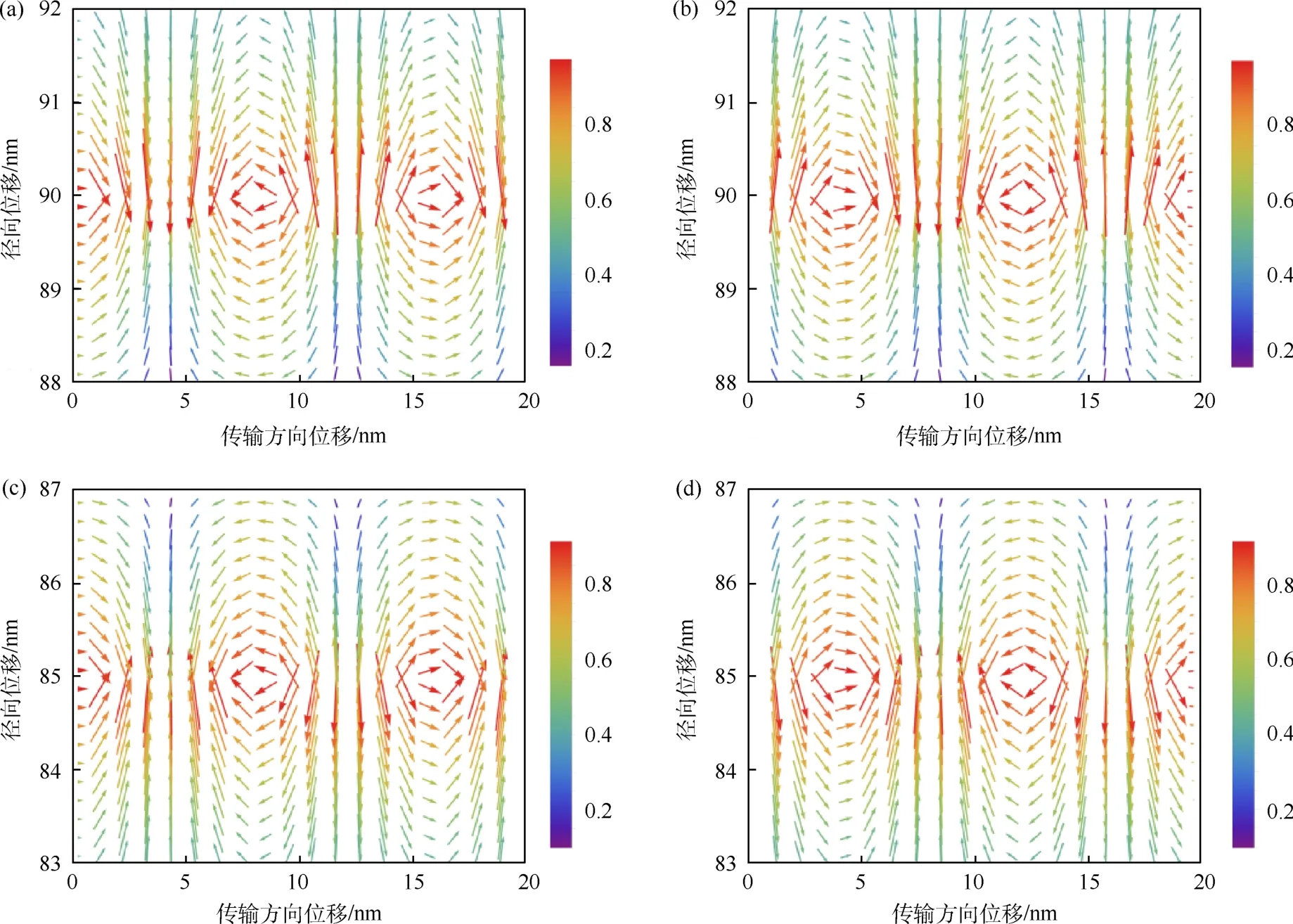
图2 SPP 1阶模不同时刻内外表面上的电场投影
2 圆筒形金属波导上SPP的自旋特性
具体从理论上讨论本征模携带的自旋具有的特性.分析圆筒外表面情况,取r=91 nm(距离外表面 1 nm),θ=0,z=0.圆筒上 SPP本征模的周期对称性和旋转对称性决定了研究这一场点可以得到外表面上具有共性的结论.计算了1和30阶模的SPP电场在1个周期内的变化(图3).3条曲线分别代表3个电场分量.Ez和Eθ有相同的位相,但是Er位相超前1/4周期,正是这种位相差造成了电场的旋转.其中Er与Ez的位相差造成了电场以θ方向为轴的旋转,Er与Eθ的位相差造成了以z方向为轴的电场旋转.也就是说,前者贡献了横向自旋分量,后者贡献了传输方向的自旋分量.Eθ和Ez没有位相差,所以,二者不在r方向形成自旋分量.1阶模式的Eθ很小,计算表明0阶模的Eθ=0,这一现象与无限大平面上的SPP相同,后者是横磁波(transverse magnetic wave,TM 波)[10].Eθ随着阶数增大而减小,因此,阶数越低,横向自旋越大.相同的结论,在内表面依然成立.

图3 SPP电场强度在1个周期内的变化
通过具体计算来证实这个结论.对于时谐波,具有以下特点[23-24]:
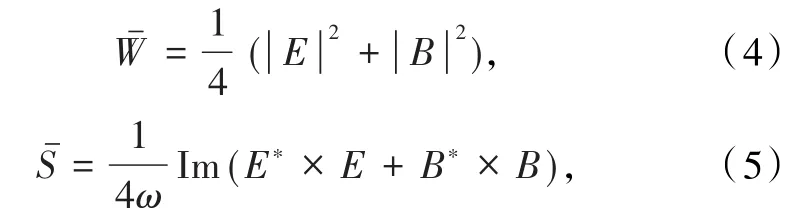

式中s表示单个光子的平均自旋角动量,为平均光子数.取ℏ =1,将式(4)~(7)进行联立,则SPP波的光子平均自旋应该满足

电磁场本征模形式如A(kz,kjr)ei(nθ+kzz-wt)的表达式,决定了光子平均自旋的大小与θ和z无关,这是金属圆筒旋转对称性的体现.利用式(8)和求解SPP电磁场本征模得出的E和H,就可以解出SPP的s与r的关系.SPP 1~30阶模式的光子平均自旋关系如图4所示.可知,各阶模式的SPP光子自旋是随模式数依次分布的,且模式数越小时,分布得越密集.为了便于观察,仅给出了其中部分阶数的图像.
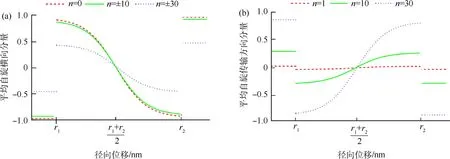
图4 不同模式下光子平均自旋各分量
SPP主要集中在金属圆筒内外表面处,在圆筒的内外表面上,SPP在低阶模式下的光子自旋几乎完全是横向的,其传输方向的自旋分量接近0,这完全符合本文的预测.而在SPP模式较高的情况下,光子自旋角动量中z分量所占比例越来越大,当SPP的阶数为30时,其自旋角动量的z分量明显大于θ分量.
模式数为相反数的SPP横向自旋(sθ)的图像完全一致,但其传输方向自旋(sz)是沿横轴镜像对称的,图4(b)中未给出负模式数图像,这说明SPP携带的横向自旋信息是不对称的,即横向自旋与轨道呈现出一种锁定关系,这种锁定性随着模式的增大而减弱.
对于SPP横向自旋呈现出的轨道-自旋锁定关系,可以分别用右手和左手螺旋定则描述:在圆筒外表面上的SPP,其横向自旋符合右手螺旋定则,大拇指指向波的传播方向,四指所指方向即为对应位置上的横向自旋取向.与之相反,圆筒内表面上SPP的横向自旋符合的是左手螺旋定则.
Henry和 Hopfield[8]指出,无限大金属-电介质平面上的SPP,其横向自旋满足
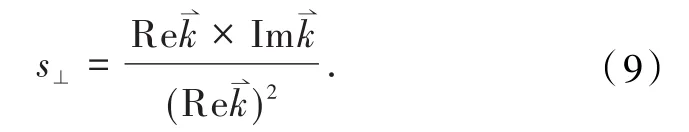
平面模型下,SPP模式的唯一性决定了平面上SPP的s⊥有着固定的大小,而圆筒形金属波导上SPP的sθ随着本征模式的变化有着不同的大小.这意味着比起在平面上,具体求解圆筒形波导上激发的具有PSHE的SPP问题更为复杂.
3 结 论
利用解析方法推导了圆筒形金属波导中的电磁场本征模,并根据计算结果研究了本征模所携带的光子自旋的特性.研究结果显示:(1)自旋特性与本征模的阶数有关,阶数越低,横向自旋分量越大,因此,在利用横向自旋传递信息时,应尽量依靠低阶模;(2)无论什么模式下,横向自旋与传播方向均具备锁定关系:即在圆筒内,横向自旋方向遵循左手螺旋定则;在圆筒外部,遵循右手螺旋定则.以上结果既可为光子通信提供参考,又可为圆筒形波导中的PSHE提供理论基础.
