基于自适应超螺旋滑模的光电平台稳定控制

张 鹏，邓 晗，王 晶，陈仁涛

（中国电子科技集团公司第二十七研究所，河南 郑州450000）

稳定性是体现光电平台伺服能力的重要指标。随着超远距离探测指示、行进间工作等功能需求的提出，稳定控制越来越受到众多专家学者的关注，成为一个重要的研究方向。传统的串级PID控制通过提高系统速度带宽来增强，但常常受所选用惯性器件、执行器的能力限制，会带来成本上的较大增幅，而且会降低系统的稳定裕度。滑模控制（SMC，Sliding-Mode-Control）由于其对匹配不确定性和扰动的有效抑制，在稳定平台控制中被广泛应用[1-4]。然而，传统一阶滑模算法存在抖振问题[5]，不仅难以实现，而且可能威胁伺服系统的安全性。

超螺旋（STSMC，Super-Twisting-Sliding-Mode-Control）算法[6]是一类结构简单的高阶滑模算法，能有效抑制抖振问题，且仅需要系统的一阶滑模信息。然而，设计超螺旋算法的参数需要已知外界扰动时间导数的上界[7]，这限制了其在实际系统中的应用。Shtessel等[8]提出了一种自适应超螺旋算法，但需要外界扰动满足特定的假设条件。李鹏[9]提出了一种仅需要扰动时间导数有界的自适应超螺旋算法。Utkin等[10]基于一阶滤波器实现了对超螺旋算法参数的自适应估计。然而，这些算法都是针对一阶SISO系统设计的，而且自适应律也相对复杂。

针对运动载体上光电平台的稳定控制问题，本文设计了一类基于自适应超螺旋算法（ASTSMC，Adaptive-Super-Twisting-Sliding-Mode-Control）的控制器。该控制器在保持传统滑模控制精度高、鲁棒性强等优点的同时结构简单、限制条件少、能有效抑制控制抖振。首先，建立了光电稳定平台的机电一体化动力学模型。其次，将原系统根据方位、俯仰方向解耦为两个子系统，并设计了自适应超螺旋控制器来确保子系统的状态收敛到滑模面上。最后，根据光电平台的典型应用环境进行了数值仿真，并将所设计的控制算法与传统算法进行了对比。

1 机电一体化动力学建模

光电稳定平台一般采用两轴-两框架的结构设计，这种结构设计可以将稳定平台在滚转方向之外的运动分解到方位轴和俯仰轴两个正交的方向上，使两轴间的运动耦合很小。在本文中，建模时假设稳定平台的动力学模型在方位轴和俯仰轴上相互独立，针对单轴建立模型来进行外界扰动的估计和抑制。

假设稳定平台在大地水平坐标系中滚转角为0，那么它在方位轴上的动力学模型如下：

式（1）中，θ为稳定平台方位框架在大地水平坐标系中的方位角，ω为稳定平台方位框架在大地水平坐标系中的方位角速度，J为稳定平台在方位轴上的转动惯量，Tc为方位轴上的控制力矩，Tf为方位轴系上的摩擦力矩，Tr为方位轴上的外界扰动力矩，主要由质量不平衡扰动，轴系线绕和风阻扰动构成。

对于高精度的稳定平台，通常采用力矩电机直驱的传动方式来减少传动齿轮或连杆带来的机械误差。在本文中，主要针对永磁同步电机（PMSM，Permanent-Magnet-Synchronous-Motor）直驱型光电稳定平台进行研究。因此，式（2）中的Tc即永磁同步电机的输出力矩。

建立PMSM在d-q坐标系中的转矩方程为：

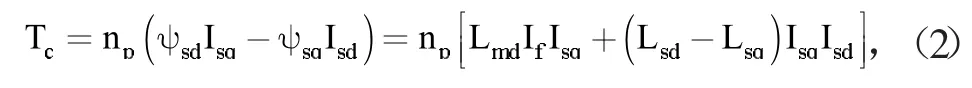
式（2）中，np为永磁同步电机的磁极对数，ψsd为在直轴磁链，Isd为在直轴电流，ψsq为在交轴磁链，Isq为在交轴电流，Lsd为等效两相定子绕组直轴自感，Lsq为等效两项定子绕组交轴自感，Lmd为直轴定子与转子绕组间的互感，If为虚拟励磁电流，为常数。由式（2）可知，PMSM的输出力矩主要与其在各轴上的电流有关。因此，建立PMSM在d-q坐标系中的电流状态方程为：

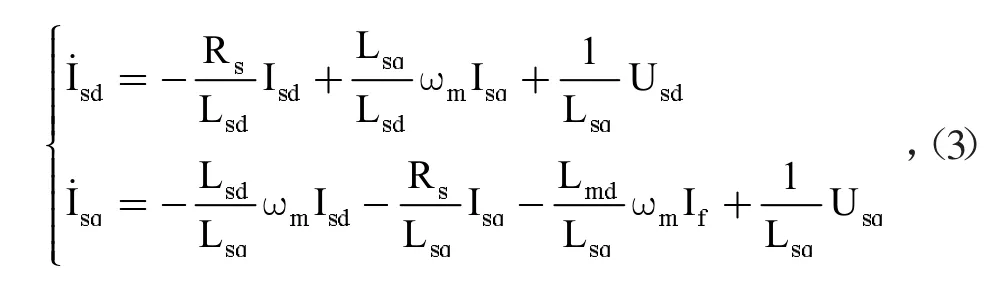
式（3）中，ωm为电机转动的角速度，Rs为电机两项绕组间的电阻值。由于电机与框架采用直驱的传动形式，电机转动的角速度与稳定平台的框架角速度ωk是等价的，即：

当采用id=0控制策略的矢量控制时，可以将PMSM的直轴电流尽量减小，从而提高能量利用效率。在建模时假设PMSM采用了理想的矢量控制，那么式（3）可以简化为如下形式：

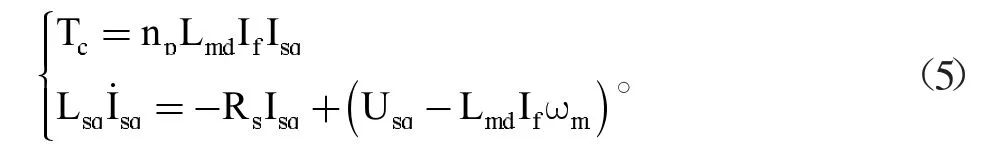
而由于母线电流I，母线电压U为d-q坐标系中电流、电压的矢量和，当Id=0时，我们可以将式（5）改写为：

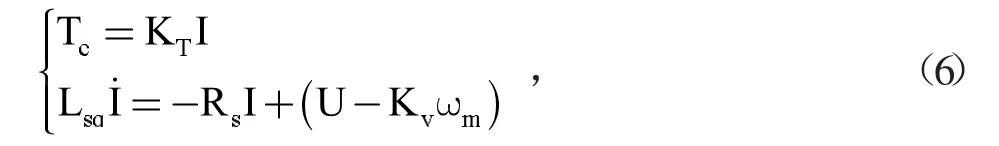
式（6）中，KT＝npLmdIf为电机的等效力矩系数，Kv=LmdIf为电机的等效反电动势系数。

稳定平台的外部扰动力矩主要为轴系上的摩擦力Tf和风扰力矩Tr，其中摩擦力Tf是与稳定平台的框架角速度相关的非线性函数[11]，其模型如下：

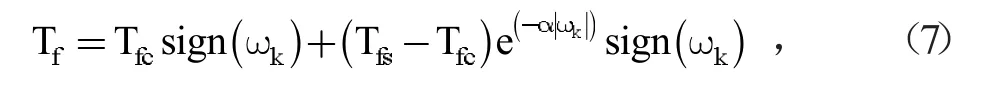
式（7）中，Tfc为库伦摩擦力，Tfs为静摩擦力，α为衰减时间系数，ωk为稳定平台的框架角速度，其与大地水平坐标系下的方位角速度关系为：

式（8）中，ωh为车体在大地水平坐标系下的角速度。

稳定平台收到的风扰力矩Tr可以认为是与其框架角相关的函数，大致上总与偏离框架角中心位置在方向上相反，在数值上正相关。Tr的简化模型如下：

式（9）中，kr为线扰力矩系数，假设为常数，θk为框架角，其与稳定平台在大地水平坐标系中的方位角θ存在如下关系：

式（10）中，θh为车体在大地水平坐标系下的方位角。

综合式（1）-（10），稳定平台所在的机电一体化模型如式（11）所示。

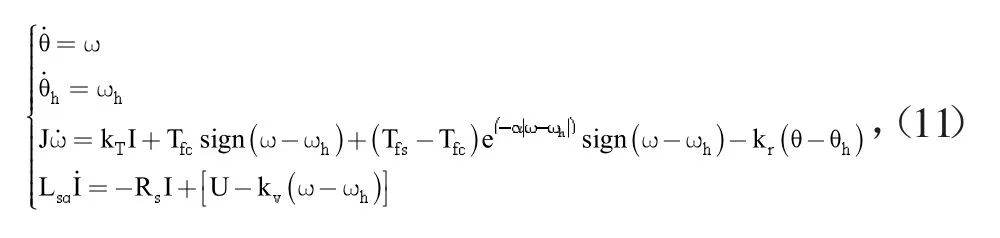
式（11）中，θ为稳定平台指向在大地水平坐标系中的方位角，θh为车头方向在大地水平坐标系中的方位角，ω为稳定平台指向在大地水平坐标系中的方位角速度，ωh为车体指向在大地水平坐标系中的方位角速度，J为稳定平台框架与负载在方位轴上的转动惯量，Tfc为库伦摩擦力，Tfs为静摩擦力，α为衰减时间系数，kr为线扰力矩系数，kT为电机力矩系数，kv为电机反电动势系数，I为电机母线电流大小，Lsq为电机交轴自感，Rs为电机相间电阻，U为电机母线电压大小。

2 基于ASTSMC的控制器设计

定义方位轴上的稳定误差为：

其中，θd为保持的空间指向，为常值。那么，将式（12）代入式（11），可得光电平台稳定控制的误差方程为：

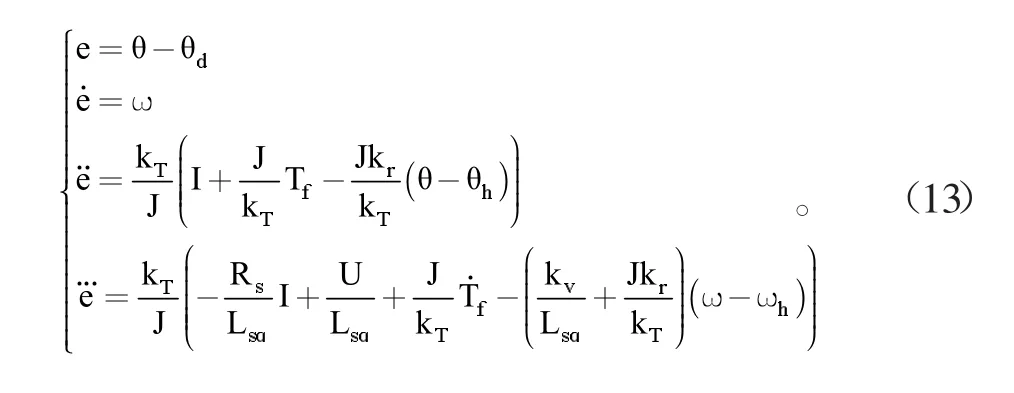
采用反步法设计滑模控制器，定义一级滑模面为：

定义二级滑模面为：

那么联立式（13）-（15），可得滑模状态方程为：

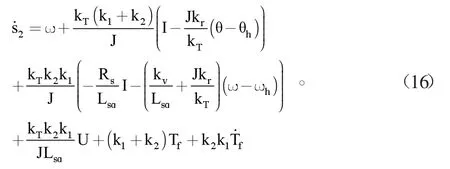
设计控制器为：

其中，Uff为前馈控制，其表达式如下：

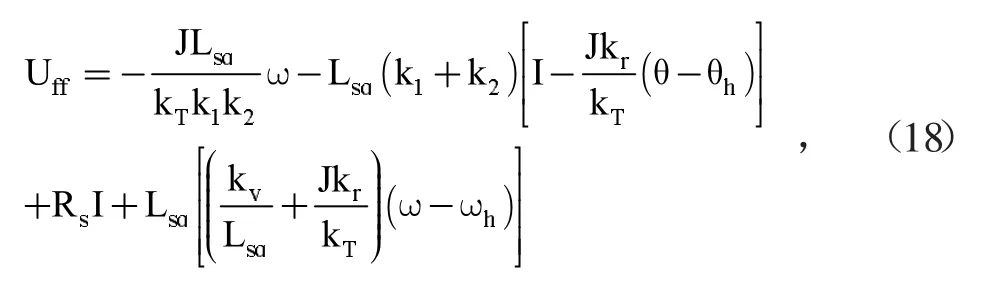
其中，Ufb为自适应超螺旋滑模控制，其表达式如下：

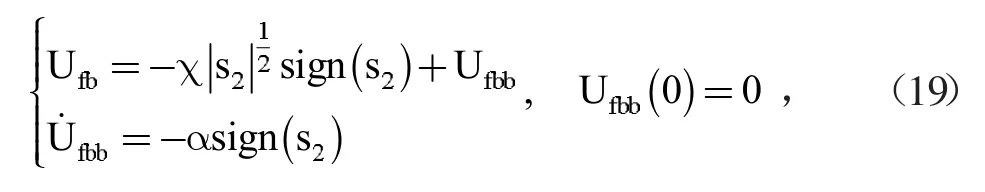
式（19）中，χ 为非零常数，α 为自适应参数且 α（0）=0，自适应律为：

定理1[12]：对于符合动力学模型式（13）和假设1的镇定控制问题，采用式（17）-（20）的自适应超螺旋控制。若控制器参数满足χ＞2，则可以系统能收敛到滑模流形

由上述定理可证，本文设计的自适应超螺旋控制能够使光电平台相对惯性系稳定。

3 仿真分析

我们在Matlab的Simulink环境下搭建模型验证本文所提出控制算法的有效性，并与传统串级PID控制进行对比分析。Simulink环境下根据式（11）搭建光电平台的机电一体化模型如图1所示，搭建ASTSMC控制器如图2所示。

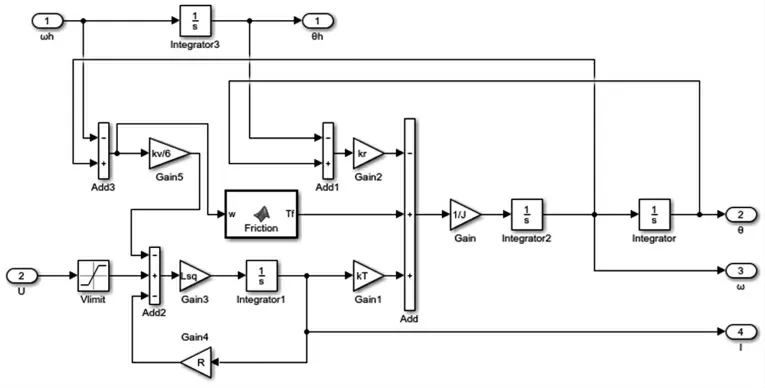
图1 光电平台机电一体化模型

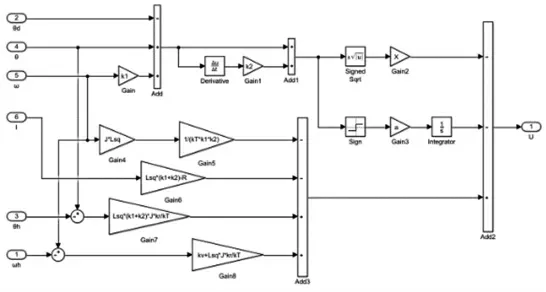
图2 ASTSMC控制器模型

模型与控制器参数设置如表1所示。

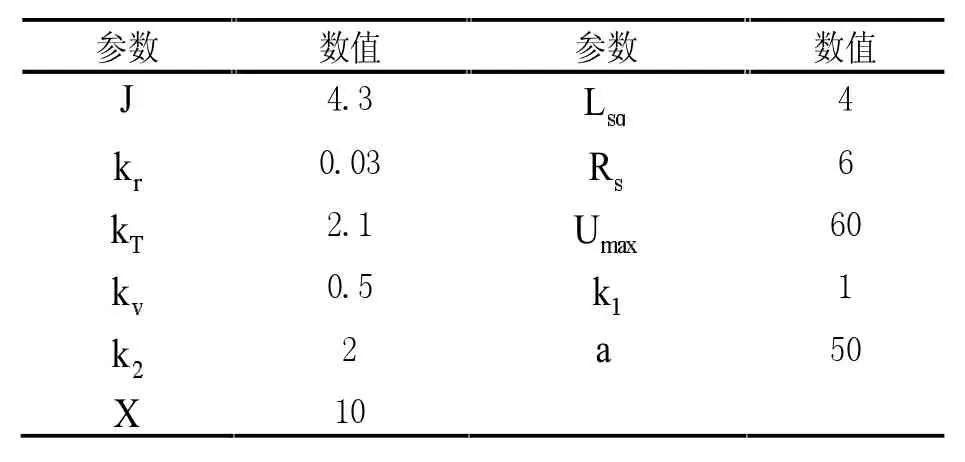
表1 仿真中的参数设置

设置车体扰动θh为7°/1Hz，在Simulink环境下进行仿真分析，并将ASTSMC与传统串级PID控制进行对比分析，仿真结果如图3所示。从图中可以看出，在典型扰动环境下，ASTSMC控制能够有效使光电平台稳定，且稳定精度优于0.01°，与传统串级PID控制下的稳定精度相比有明显提高。

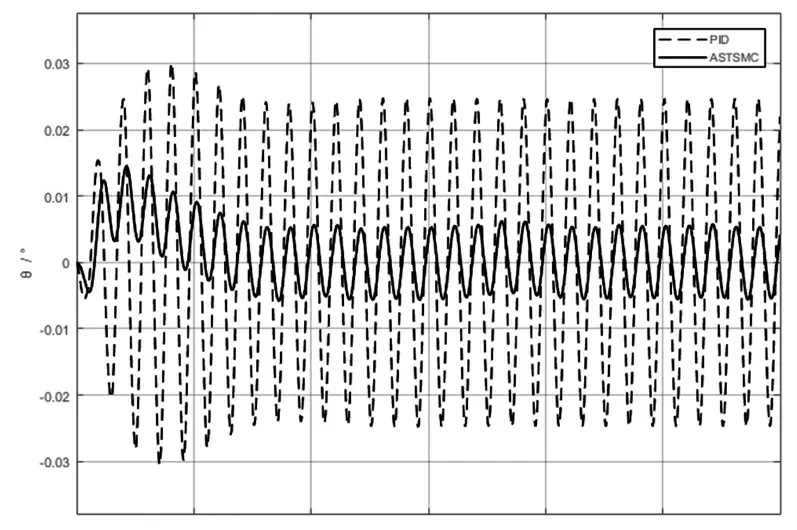
图3 ASTSMC与PID的稳定性能对比

4 结论

本文首先建立了光电稳定平台的机电一体化动力学模型，然后在此基础上设计了一类自适应超螺旋控制器来进行确保平台的稳定性能，最后通过对光电平台的典型应用环境进行数值仿真表明，本文所设计的控制器能够有效使光电平台在惯性系下稳定，且性能优于传统串级PID控制算法。