基于一种改进的二分法的MPPT算法

张继勇，马一鸣，李 旺，张 毅，史旺旺

（扬州大学 电气与能源动力工程学院，江苏 扬州225009）

光伏发电的并网化、规模化已成为未来电力发展的主要趋势，如何提高光伏发电效率、增加并网容量等光伏发电重难点问题依然没有解决。目前为提高光伏发电效率所采用的改进太阳能电池板及改进并网系统中控制器和逆变器等手段虽可以提高发电效率，但改进成本较高。但对MPPT算法的改进因成本低且效果明显已成为众多学者的首选方案。国内外已研究出多种MPPT算法及其改进法，文献[2]提出二分法测量最大功率跟踪，虽提及不同初始步长对跟踪特性的影响，但步长依然是固定的；文献[3]提出变步长PO法加快定位MPP，但纹波较大。针对上述问题，本文提出一种基于混合步长改进的二分算法，利用二分法的快速收敛性和混合步长的准确性迅速找到最大功率点，不仅可以避免普通算法在最大功率点附近产生振荡现象，还可以提高跟踪速率，避免能量损失，并通过仿真验证此方法的可行性与准确性。

1 光伏电池及变步长原理

1.1 光伏电池的模型

图1为光伏电池等效电路。IL为流过负载的电流；Iph为光生电流源产生的光生电流；Rsh为并联电阻；I0为饱和电流；q为单位电子电量；n为二极管因子；K为玻尔兹曼常数；T为光伏电池绝对温度；Rs为串联电阻。

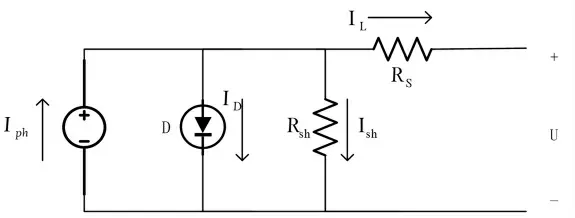
图1 光伏电池等效电路

图1中：

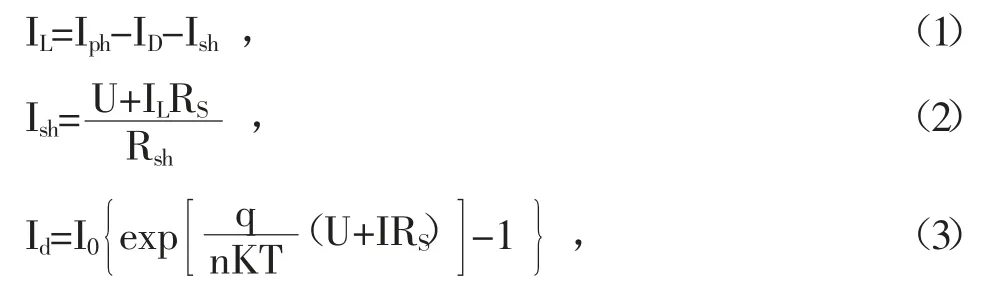
由上式可以推导出：

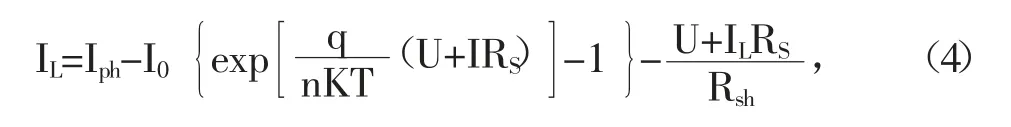
一般来说，U+IL/Rsh＜＜Iph，假定Iph=Isc，当Rsh数值很大，而Rs数值很小计算时几乎可以忽略不计。因此，令C1=I0/Isc，C2=nKT/Uocq，式（4）可简化为：

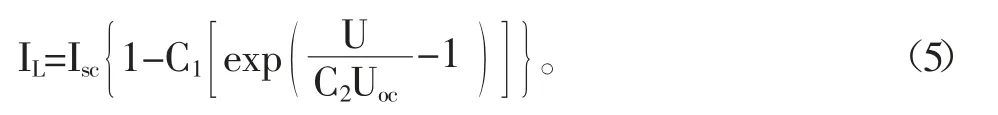
1.2 光伏电池的输出特性

光伏电池是一种非线性直流电源，它的伏安特性受外界环境的影响较大。当光照强度和温度等发生变化时，它产生的电压和电流都非恒定，在接近开路电压时，电流呈下降趋势，之后因电压的稳定电流可近似为恒定。

1.2.1 光照强度恒定，温度变化

设光照强度S=100W/m2，外界温度分别为T=25℃，35℃，45℃时，仿真结果如图2所示。

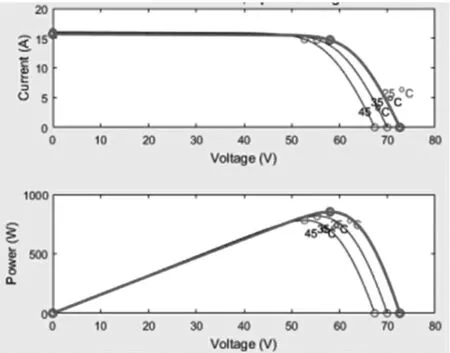
图2 温度变化光伏曲线

由图2知，在光照强度恒定情况下，光伏阵列的开路电压和短路电流会随温度变化而改变。开路电压随温度升高而降低，短路电流随温度升高而略有增加。

1.2.2 温度恒定，光照强度改变

设外界温度T=25℃，光照强度分别为S=100W/m2，500W/m2，1000W/m2时，仿真结果如图3所示。

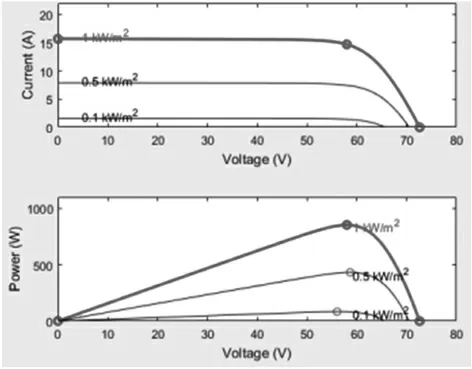
图3 光强变化光伏曲线

由图2、图3可知，电压随着外界环境的变化而改变，即MPP也随之改变。设1kW/m2的V-P与V-I的交点为点A；同理0.5kW/m2时的MPP点为点B。再设一个中间变量δ，设光强从1kW/m2突然降到0.5kW/m2时，此时工作点从A切换到B，因此δ也改变。

其中：V、I分别为PV的输出电压和输出电流；c是一个常数；q为单位电子电量；n为二极管因子；K为玻尔兹曼常数；T为光伏电池的绝对温度。

通过计算得到：δB＞δmax，即点B不在预估范围之内，因此步长△D为：

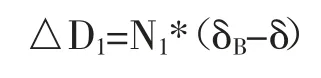
同理，当光强从0.5kW/m2上升到1kW/m2时，即点B立即切换到点A，此时点D的δ值要小于δmin，即点D位于δmin和δmax的范围外。此时步长△D为：

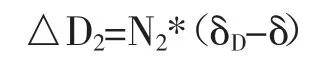
与传统的固定步长相比，这里运用N1和N2两个不同的比例参数来确定光强上升和下降情况下的步长，避免了步长过大或过小。

2 最大功率跟踪算法分析

2.1 算法原理

光伏MPPT技术的应用十分广泛，如P&O法、电导增量法已普遍应用于实际生活，现有技术的优点是控制方法简单且易操作，但这两种算法的缺点是扰动步长的固定性。如果扰动步长过大，就会导致MPP振荡较大；如果扰动步长过小，就会导致启动时间过长，二者都会导致能量的流失。为了解决这一问题，本文提出一种变步长二分法，并对算法做出优化，如图4所示。

图4 变步长二分法原理图

变步长二分法原理是利用数学的二分法，结合DC/DC变换电路，利用二分取占空比值来控制MOS管的开通与关断。该算法目的是在最短时间内找到MPP对应的电压。

2.2 具体方法

（1）假设太阳能电池的初始工作电压为U1、输出功率为P1，此时MOS管的工作占空比为D1。假设所取电压值位于最大功率点的左侧，将此周期的占空比D1乘以2，即D2=2D1，新占空比D2即为下一周期占空比值。

（2）设MOS管的新占空比调为D2，太阳能电池的初始工作电压为U2，输出功率为P2。假设此时电压的值在MPP右侧，则将D2与△D1二分取中点，即D3=（△D1+D）2/2，新的占空比D3为下一周期占空比值。

（3）设MOS管的新占空比调为D3，工作电压为U3，输出功率为P3。假设此时电压取值在MPP的左侧，则将D3与△D2二分取中点，即D4=（△D2+D3）/2，新的占空比D4即为下一周期占空比值。

同理一直重复此过程，直到对应的电压值达到MPP位置。结果表明该算法可成功寻找到MPPT，使太阳能电池的输出功率达到最优。

变步长二分法的控制原理如下：通过数学二分法，求出占空比闭合区间[0，1]内太阳能电池最大输出功率所对应的值，即太阳能电池的最大功率点。变步长二分法的控制流程如图5所示。

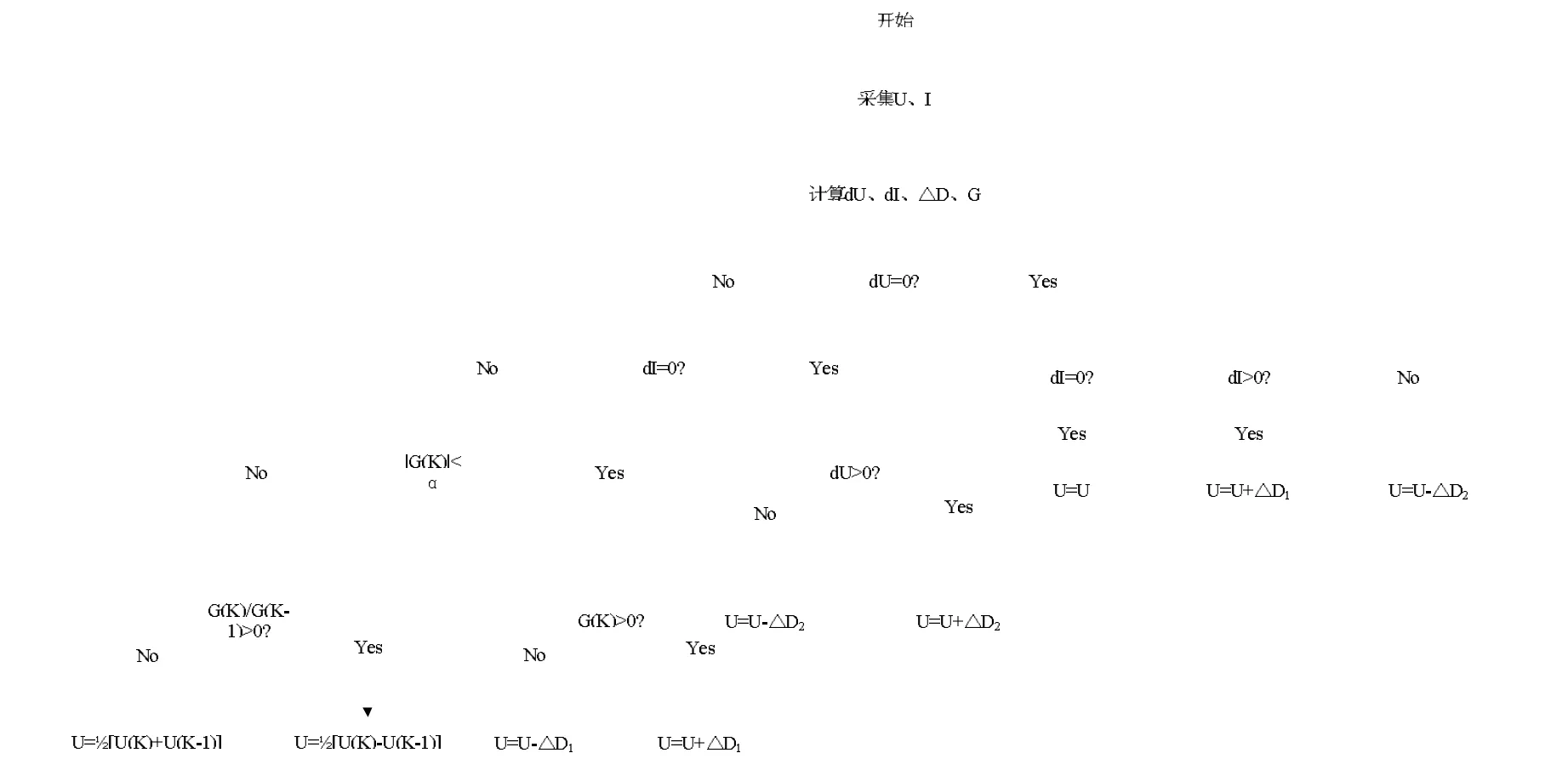
图5 变步长二分法算法流程

从图5中可以看出，变步长二分法同P&O法相比具有如下优点：

（1）初期利用变步长的优势可迅速锁定最大功率点的大概位置，缩短优化时间。

（2）当大概位置确定后，再通过减小步长实现工作点在最大功率点附近产生的震荡现象，大大提高系统的稳定性，避免能量的不必要损失。

3 仿真模型

建立图6所示光伏MPPT仿真模型，利用Boost型DC/DC变换电路，使用MATLAB/Simulink对变步长二分法、传统二分法和P&O法进行仿真与比较。

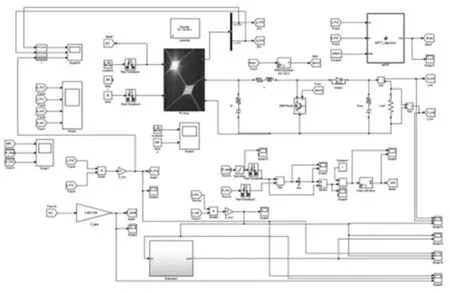
图6 光伏MPPT仿真电路图

4 仿真结果

仿真条件设定：

（1）设外界环境恒定，光照强度1kW/m2，温度25℃。假定环境条件发生变化，光强从0kW/m2上升到0.3kW/m2再上升到0.5kW/m2、1kW/m2，最后再降至0kW/m2。两种光强变化情况如图7所示。

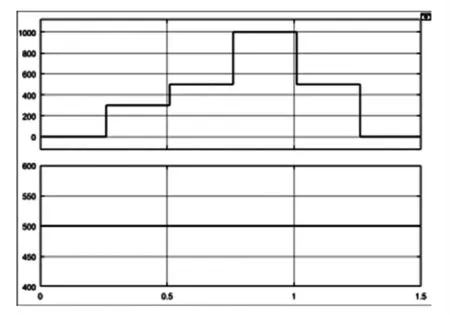
图7 两种光强变化情况

（2）MOS管的工作频率设定为10kHz，扰动观察法的扰动步长设定为△U=0.01V。

从图8知，在光强不变的情况下，变步长二分法在0.0095s左右能达到系统稳态，P&O法和传统二分法在0.015s左右才达到相同效果。

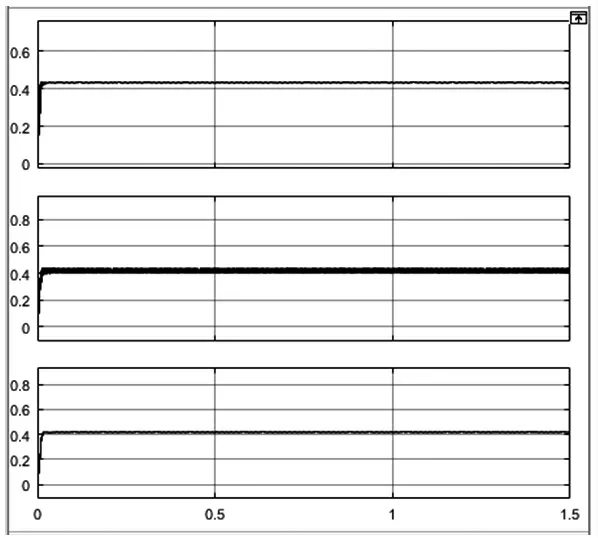
图8 光强不变三种算法比较

从图9知，在不同的算法下，最大功率点处的稳定性和精度稍有不同。P&O法和传统二分法的功率曲线瑕疵较大，有较大的波动且波纹明显。但变步长二分法的功率曲线平滑且稳定，纹波较小，符合预期目标。

当步长从固定到变化后，从图9看出0.25-0.35s有较小振荡，1-1.1s处振荡与其他方法相比较小。由此可见，变步长对系统跟踪性能是有提高的，它可以快速精确地追踪到系统的MPP。

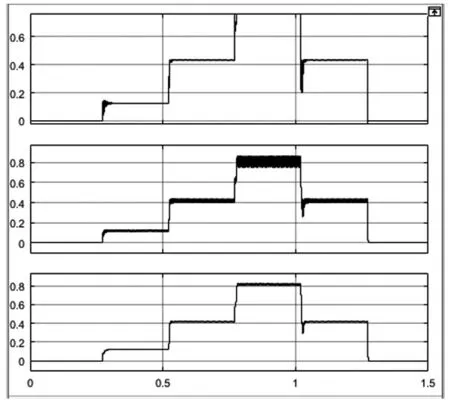
图9 光强变化三种算法比较

5 结束语

在MATLAB/Simulink中基于对P&O法、传统二分法与改进二分法就最大功率跟踪问题进行了仿真，在光照强度相同和不同情况下，对比分析这三种方法的优缺点，仿真结果表明变步长二分法能更快地找到最大功率点，不仅提高了跟踪的速度，还降低了系统在MPP附近的振荡现象，在保证系统稳定的情况下较好地获得最大功率。