轨道车辆轴箱传感用压电梁振动发电特性分析

2021-08-21黄如艳郑树彬丁亚琦彭乐乐

噪声与振动控制 2021年4期

黄如艳，周炯，郑树彬，丁亚琦，彭乐乐

（1.上海工程技术大学城市轨道交通学院，上海201620；2.上海地铁维护保障有限公司，上海200031）

将传感器安装于轨道车辆轴箱处是实现车-轨动力学测量、轴及轴承检测的主要手段之一[1–2]。随着传感器自身功耗的降低[3]，通过吸收环境能量实现自驱动式工作已经成为传感器一种发展趋势[4–5]。受轮轨作用力的影响，轨道车辆在运行过程中产生较大的低频振动，利用压电梁能量俘获器收集振动能量[6]可为车载微型传感器供电。

如何在轨道车辆所处低频振动环境中实现压电梁能量转换最大化是解决传感器供电的关键。曹东兴等[7]根据矩阵传递法设计二级阶梯变厚度悬臂梁，通过仿真研究梁几何参数对固有频率的影响，获得输出电压频响曲线，通过改变几何参数实现输出电压最大从而提高发电能力。夏光辉等[8]采用Hamilton变分原理建立端部附加质量块压电梁的非线性机电耦合运动微分方程，利用增加质量块降低固有频率，拓宽俘能频带从而实现发电能力最大化。杨菁等[9]利用分布参数模型解析解修正集总参数模型的近似解，得到梁自由端与固定端宽度比随系统固有频率变化的规律，有利于系统与环境谐振从而提高发电能力。满大伟等[10]采用多尺度法建立双稳态悬臂梁式压电俘能分布参数模型，得到减小系统阻尼比可拓宽频带并获得较高输出的结论，通过优化设计和调节参数实现能量转化效率最大化。王红艳等[11]通过建立车辆垂向振动模型获得车体振动响应，利用有限元法揭示俘能器基频、外界负载和车速这些影响因素与输出功率内在联系，达到通过调节影响因素从而提高俘能器发电性能的目的。张梦倩等[12]基于不同的边界条件探究压电悬臂梁的耦合特性，建立机电耦合系统数学模型，通过加入电感建立2阶电路，可较大程度地提高能量转换效率。

以上方法多是通过改变压电俘能器的结构参数实现环境振动主频率与结构固有频率相适应，以达到能量转换最大化的目的。而针对适应于地铁运行环境中的低频强冲击振动的能量收集器的振动发电特性研究较少。文中利用小弯曲变形理论建立压电梁的机电耦合模型并通过搭建实验台验证了模型正确性。基于此模型利用仿真手段获取了压电梁几何及材料参数、振动频率和附加质量块与输出功率关系。并结合列车实测振动信号得到了车辆轴箱低频振动主频特征，获取了适合于轨道车辆轴箱传感用压电梁参数，实现了输出功率最大化。

1 压电梁结构及机电耦合建模

轨道车辆轴箱传感用压电梁结构如图1 所示。其由一块金属基底、两片压电陶瓷和附加质量块m组成，压电陶瓷分别固定在金属基底上下表面组成压电梁，两端固定，附加质量块粘连在梁上下表面中心处。

图1 压电梁结构图

由于压电梁长度l远大于其厚度h和宽度b，且梁振动时的挠度较小，可以使用梁的小弯曲理论进行分析。设X轴和Y轴与梁的中性面Zs重合，梁的中性面为图1 中虚线所在的平面，中性面到梁的上下表面距离为h/2。hm为金属材料厚度，hp为压电陶瓷厚度，金属材料与梁厚度比为α=hm/h，hp=(1-α)h/2。由于附加质量块面积远小于金属基底面积，振动时可将其等效为作用在梁中点处的集中载荷F。在载荷F的作用下，压电梁发生形变如图2所示。

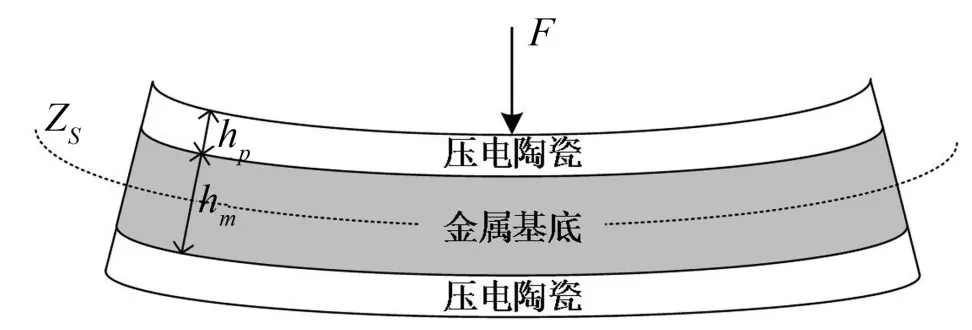
图2 受力分析图

压电梁受力时厚度比α是应力和应变的函数，压电梁的边界条件为第二类边界条件，且由材料的弹性理论和压电振动方程，根据梁的一维应力近似原理可得压电陶瓷的本构方程式如式(1)至式(2)所示[13]：

其中：σx为X轴方向上的应力；εx为X轴方向上的应变；Ep是压电陶瓷的杨氏模量；Ez是由正压电效应产生的内电场强度；Dz是在外力和电场强度共同作用下产生的电位移，大小用电荷密度来表征；εσ33是介电常数；d31为压电梁在Z轴方向上的压电应变常数。式（2）表明Dz是表征压电梁发电量大小的关键参数。

压电梁的力矩M和截面抗弯刚度D用微分表示为

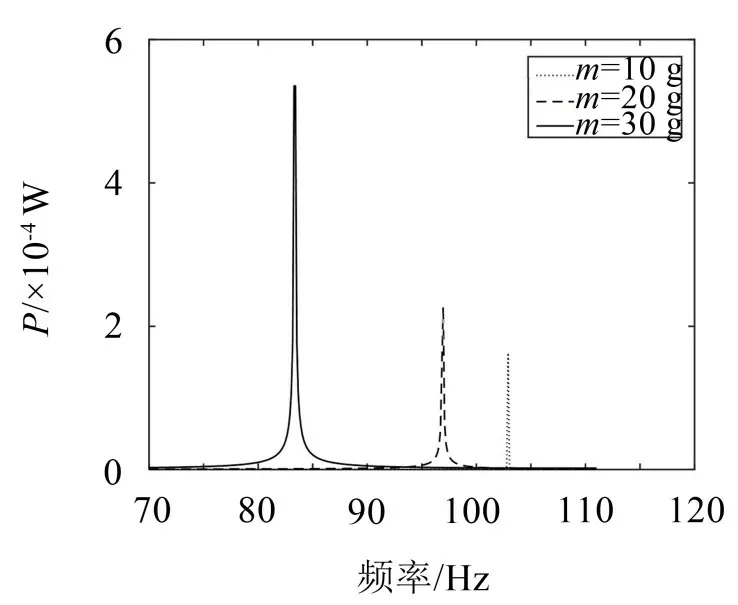
其中：σm=Emεx是金属材料的应力，n为压电陶瓷片数，z为Z轴上点到中性面的距离。假设外界振幅为H，频率为ω，则梁中点处的受力为F(t)=2mω2Hsin(ωt)，在梁上0

将式（4）代入式（3），则能求解出Ez如式（5）所示：

式中：A=3(1-α)-3(1-α)2+ (1-α)3，B=2(1-α)- (1-α)2，β=Em/Ep，将Ez代入式（6）即可求得压电陶瓷上下两个表面之间的输出平均电压：

由于压电陶瓷具有一定的厚度和硬度，其应变的大小可以等效为均匀应变，此时z=±(1+α)h/4。将Ez代入式（2）可求得压电梁电位移，压电梁电荷量Q为在X截面处的电荷密度Dz对梁长l的积分，则有：

根据电能公式W=压电梁的发电量计算公式可以表达为

2 轨道车辆轴箱振动特性分析

采用如图3 所示测试方法，将DFT1301 型号的加速度传感器通过支架安装于车辆轴箱轴端盖上，并在上海地铁5号线剑川路至闵行开发区站间进行测试，通过Wavebook516E 型号的数据采集仪采集列车的振动信号并将数据保存在计算机中，数据采样频率为10 kHz。图4为振动数据的时域图，图5为经过傅里叶变换后得到的频域图。

图3 现场安装测试图

从图4中可以看出轴箱振动加速度具有冲击特性，且幅值较大，最大值接近25 g。进一步对该组数据进行傅里叶变换，并选取振动能量集中的低频部分作为研究对象，结果如图5所示。从图5中可以看出，轨道车辆轴箱振动主频段位于80 Hz 与90 Hz之间。

图4 车辆轴箱振动数据时域图

图5 车辆轴箱振动数据频域图

3 模型验证

为了验证压电梁发电模型的正确性，搭建实验平台如图6所示。该实验平台由主机、信号发生器、功率放大器、激振台、示波器、显示屏和压电梁组成。设置频率为1 Hz、幅值为2 m/s2的正弦振动为激励信号，经信号发生器和功率放大器将信号传输至激振台产生振动，激振台上固定压电梁，尺寸为：l=84 mm，h=7.5 mm，b=30 mm，其由铍铜金属基底和PZT-5H压电陶瓷组成，且金属基底厚度与梁厚度比α=0.3，并在梁中心处放置30 g 附加质量块。在压电梁上下表面各引出一条导线，利用示波器读取压电梁两端电压。

图6 实验平台

图7 为由实验测得的压电梁电压波形图，由图可看出电压的直流有效值为5.16 V，铍铜杨氏模量为13 GPa，PZT-5 H压电陶瓷的杨氏模量为7.1 GPa，两者杨氏模量比β=1.83，介电常数为1 470，根据式（8）计算出电压值为5.3 V，偏差为0.14 V，计算结果与实验数据基本吻合，这证明了所建立的压电梁机电耦合模型的正确性。

图7 压电梁电压波形图

4 压电梁发电特性仿真分析

为了进一步对压电梁发电特性进行分析，基于压电梁机电耦合模型，利用MATLAB软件平台得到材料参数和驱动频率与功率之间的关系，所采用具体参数如表1所示。

表1 材料性能参数

图8 表示金属材料分别为铍铜和锰白铜、压电陶瓷分别为PZT-5H、PZT-5A和PZT-4时压电梁的输出功率和频率之间的关系曲线图。由图8可知铍铜/PZT-5H和锰白铜/PZT-5A都能够在80 Hz～90 Hz频段内产生较大的输出功率，且铍铜比锰白铜的输出功率更大。因此，若要通过压电梁充分转换车辆振动能量，应优先选用铍铜金属材料。

图8 不同材料构成的压电梁输出功率与频率的关系

图9为采用铍铜为金属基底的压电梁在不同厚度比α条件下输出功率和频率之间的关系图。

由图9可知，当厚度比α=0.3时，压电梁固有频率在85 Hz 附近，在轨道车辆轴箱主频段内。而厚度比为α=0.43 和α=0.6 时，压电梁固有频率均不在此频段内，且输出功率低。金属层厚度过大或过小都会降低压电梁的转换效率，其存在一个最佳的值，每种压电梁的最佳值如表2所示。大多集中在α=0.3附近。

图9 不同厚度比α与频率之间的关系图

表2 不同金属与压电陶瓷的压电梁最佳厚度比与输出功率

在压电梁中心处附加集中质量块的目的是在振动时增加压电陶瓷的变形量，随着附加质量块的增加，压电梁的固有频率呈减小趋势，图10 是附加质量分别为10 g、20 g 和30 g 时压电梁的输出功率和驱动频率之间的关系，由图可知附加质量块为30 g时的压电梁振动频率在85 Hz 左右，其在轨道车辆轴箱主频段内，且输出功率高。

图10 不同附加质量下输出功率与频率之间的关系

综上所述，轨道车辆低频振动主频段介于80 Hz到90 Hz 之间，在此振动环境中压电梁结构的较优配置为：在相同压电陶瓷条件下，铍铜金属材料组成的压电梁发电性能比锰白铜金属材料好；相同金属材料条件下，PZT-5H材质的压电陶瓷性能最好。由铍铜与PZT-5H 压电陶瓷组成的压电梁在厚度比α=0.26 时性能最优，且附加质量块重量为30 g 时，输出功率最大。