颗粒阻尼减振特性研究
2021-08-21陈亚楠李秋彤涂田刚
刘 艳,梁 要,陈亚楠,李秋彤,涂田刚
(1.上海材料研究所,上海200437; 2.上海消能减震工程技术研究中心,上海200437;3.上海第二工业大学环境与材料工程学院,上海201209)
颗粒阻尼是一种利用摩擦和非弹性碰撞进行能量耗散的复合阻尼技术,其结构特点是在主结构内部或外附腔体内填充颗粒,填充颗粒可以由一种颗粒组成,也可以由多种粒径的颗粒组合而成,材料通常选用钢珠、陶瓷、玻璃珠、聚氨酯等[1–3]。其阻尼机理是:主结构受到激励发生振动时,通过腔体内颗粒与颗粒、颗粒与腔体之间的摩擦、碰撞作用进行能量的转移和耗散,产生阻尼效果,进而达到降低主结构振动响应的目的[4–5]。同时颗粒阻尼器对原结构影响小,结构简单,安装方便,能有效拓宽减振频带,可应用于高辐射、高温等诸多特殊环境中[6–7]。
国内外对颗粒阻尼的研究始于上世纪80年代末,Panossian[8]通过对当时已有阻尼手段进行优劣性尤其是恶劣条件下的适用性分析之后,提出了非阻塞性颗粒阻尼器(Non-obstructive particle damping,NOPD)的概念,并通过大量实验探究了颗粒阻尼器的减振控制效果。Hollkamp等[9]为降低引起喷气发动机疲劳破坏的振动应力,同时考虑到发动机的高温环境影响,决定采用颗粒阻尼技术,以带有钻孔的悬臂梁结构评估颗粒形状、粒径、密度、被激活颗粒数目、振动水平对阻尼性能的影响。闫维明等[10]以单自由度钢框架为研究对象,通过自由振动试验,探究颗粒阻尼技术在建筑领域的减振控制机理。杨英等[11]采用离散单元法,在MATLAB环境中研究颗粒阻尼器对机械构件的振动抑制性能,提出了碰撞过程中颗粒的状态、受力及耗能大小的求解算法。
目前,国内外尽管对颗粒阻尼的减振效果进行了一定研究,但颗粒阻尼属于高度非线性阻尼,通常情况下颗粒系统内部表现出复杂的力学行为和难以描述的运动状态,其减振机理尚不明确。本研究以空心腔体为对象,建立仿真模型,针对材料类型、粒径、颗粒数目、初始位移量对减振效果的影响规律进行仿真研究,并通过试验验证模型的有效性;同时还研究了该阻尼结构在中高频段的隔振效果。
1 颗粒阻尼器模型建立
本研究基于离散单元法结合多体动力学理论进行联合仿真,建立颗粒阻尼器仿真模型。模型由上部腔体、腔体内的颗粒、中部弹簧和下部支撑板组成。首先利用多体动力学软件进行腔体、弹簧、支撑板三维模型的创建。腔体材料为45 钢,其密度为7 850 kg/m3,弹性模量为2×1011Pa,泊松比为0.285,尺寸如下:内径为180 mm,高为40 mm,外径为210 mm,高为60mm,质量为8.32 kg,弹簧刚度为100 N/mm;支撑板材料属性与腔体相同,且在支撑板与地面之间添加固定约束。
由于对颗粒阻尼器的运动学进行仿真时,主要考虑腔体结构的运动情况,因此在满足颗粒阻尼器仿真结果准确性的前提下,简化了螺栓孔等细节设计,省略了与其运动无关的构件,而颗粒阻尼器的导向装置则由软件中设置的运动副取代。图1是简化后的颗粒阻尼器装配图。

图1 颗粒阻尼器仿真模型
对软件进行基本设置时,单位选择MMKS,设置重力加速度为Y=-9 800 mm/s2。然后导出腔体结构的材料属性、边界条件等设置文件,并将其导入离散元软件。在离散元软件中对颗粒系统进行建模,设置颗粒单元生成数目、材料属性及初始条件。通过网格单元法进行颗粒接触判断,计算边界接触力,利用力和位移的关系及牛顿第二定律建立起每个颗粒单元的运动方程,再用动态松弛法迭代求解这些运动方程,从而求得颗粒的整体运动形态。其中接触力的计算是离散元理论的核心部分。仿真时采用Hertz-Mindlin无滑动接触模型,该模型以Mindlin的研究成果作为理论基础,具有计算准确、高效的性能。
最后,在多体动力学软件中的求解分析界面设置时间步长等参数,控制耦合顺利进行。完整的仿真流程如图2所示。

图2 仿真流程图
基于颗粒阻尼系统仿真模型,在密闭腔体内填充颗粒,探究颗粒阻尼对减振效果的影响。图3 显示的是自由振动工况下,未添加颗粒和添加数目为600、粒径为4 mm 的45 钢颗粒时腔体的位移时程曲线。
由图3 可知,未添加颗粒时,位移衰减缓慢,此时结构仅依靠自身阻尼进行能量耗散。当腔体内填充颗粒后,振幅衰减速率明显提高,在0.5 s时,腔体位移幅值接近于0,说明颗粒阻尼具有良好的减振作用。

图3 位移时程曲线
参数变化对结构振动特性的影响规律将在后文中进行详细探究。采用时域信号衰减法对由仿真计算得到的腔体位移数据进行处理,计算相隔j个周期的等效阻尼比,以此作为颗粒阻尼器减振性能的评价指标。
等效阻尼比的计算公式如下:

其中:δ是对数衰减率,ui是衰减曲线的第i个位移峰值,ui+j是第i+j个位移峰值,j是两个峰间隔的周期数。
通常结构阻尼比ξ较小时(ξ<0.2),上式可化简为δ=2πξ,故得:

2 颗粒阻尼器减振特性试验
为验证仿真模型的有效性,确保仿真结果可靠,采用如图4所示的试验装置对其进行试验验证。将圆柱腔体、连接板、轴承、导向轴、轴承支座、弹簧、底部钢板等组件垂直安装,下端刚性固定,上端与振动控制系统相连,圆柱形腔体内填充颗粒。试验分为自由振动和强迫振动两种工况。自由振动工况下采用初始位移激励法,在腔体顶端通过位移控制系统施加不同的初始位移量,然后释放使其自由振动;强迫振动以单频30 Hz 正弦激励为例,激励力由垂直方向的激振器提供。传感器置于腔体上表面,另一端与数据采集仪相连。试验仪器主要包括Spider数据采集仪和分析系统、传感器等。

图4 颗粒阻尼振动抑制系统试验
试验时腔体、填充颗粒及弹簧的选用等相关参数均与算例保持一致,通过试验测得颗粒阻尼器一阶固有频率为17.453 Hz。将自由振动与强迫振动工况下的颗粒阻尼器试验振动位移时间历程与仿真结果对比,分别如图5(a)和图5(b)所示。

图5 位移时程对比图
由对比可知,自由振动和强迫振动测试工况试验结果与仿真结果吻合度均较好,证明了仿真模型的有效性。图中试验数据幅值略低于仿真数据,这是由于在试验中,导向轴与轴承之间有摩擦力的存在,而摩擦力会耗散系统能量,造成误差。
在下文中,通过已验证的模型继续探究颗粒材料、数目、粒径以及初始位移量对颗粒阻尼器振动特性的影响。
3 减振性能仿真分析
3.1 颗粒参数对结构振动特性的影响
3.1.1 材料类型对减振性能的影响
通过选取不同的颗粒材料验证材料类型对颗粒阻尼器减振性能的影响,设置颗粒数目为1 200 颗,粒径为4 mm,汇总材料参数如表1所示。等效阻尼比随材料类型的变化情况如图6 所示。结果表明,当填充颗粒材料为45 钢时,等效阻尼比最大,减振效果最好;当填充玻璃颗粒时,等效阻尼比最小,减振效果最差;铅颗粒的减振效果介于两者之间。总体来讲,设计颗粒阻尼器时,从经济型和减振效果的角度考虑,钢是优越的填充材料。

表1 颗粒材料参数

图6 不同材料类型的阻尼比
3.1.2 粒径对减振性能的影响
为研究粒径对减振性能的影响,本研究选用粒径分别为4 mm、6 mm、7 mm、8 mm、10 mm、12 mm的45 钢颗粒,具体参数如表2 所示。控制颗粒总质量相同,探究相同初始位移量条件下,粒径对减振性能的影响。

表2 不同粒径下颗粒数目
结果如图7 所示。随着粒径增加,等效阻尼比先减小后趋于平缓:粒径为4 mm时,阻尼效果最佳;粒径在4 mm~6 mm 范围内时,等效阻尼比降低缓慢;粒径在6 mm~8 mm范围内时,等效阻尼比迅速降低;粒径为8 mm、10 mm、12 mm 时,等效阻尼比变化不明显。

图7 不同粒径下的阻尼比
这是因为粒径为4 mm 时,颗粒数目最多,腔体起振后,颗粒与颗粒、腔体内壁能发生充分的碰撞与摩擦,耗散更多系统能量。粒径从6 mm 变化到8 mm时,颗粒数目大幅度减少,致使颗粒间的碰撞与摩擦作用减弱,减振性能急剧下降。粒径为8 mm、10 mm、12 mm 时,颗粒数目水平较低,减振效果受到较大限制。总体来说,在颗粒总质量一定的条件下,颗粒半径越小,颗粒阻尼器减振效果就越好。
3.1.3 颗粒数目对减振性能的影响
将数目为0、200、400、600、800、1 000、1 200、1 400、1 600、1 800、2 000 的45 钢颗粒填充到腔体中,控制粒径相同,讨论相同初始位移量条件下,颗粒数目对减振性能的影响。结果如图8 所示,减振效果随着颗粒数目的增加先增强后减弱,存在最优值。在实际工程应用中,控制质量比(颗粒总质量与腔体质量之比)在一定范围内,通过改变颗粒数目增加颗粒总质量,能有效增加碰撞阻尼和摩擦阻尼,消耗更多系统能量。当颗粒数目增加到一定程度,导致颗粒堆积,颗粒的有效碰撞次数降低,颗粒阻尼增加速率就会减缓。当颗粒数目达到最优条件时,由于颗粒系统运动空间有限,继续增加颗粒数目,会使颗粒难以发挥碰撞耗能作用,等效阻尼比降低,减振效果下降。

图8 不同颗粒数目下的阻尼比
3.1.4 初始位移量对减振性能的影响
本节以45 钢为例,颗粒数目取为1 200,粒径是4 mm,分别设置5 mm、10 mm、15 mm、20 mm、25 mm、30 mm、35 mm、40 mm共8组初始位移量,探究其对减振性能的影响。由图9 可知,随着初始位移量的增大,颗粒阻尼器减振效果增强,这是因为增大位移量可以加剧腔体振动,使颗粒与颗粒、颗粒与腔体间充分碰撞和摩擦,耗散能量就会增多。当进一步增加初始位移量,等效阻尼比增加缓慢,最终趋于平缓。

图9 不同初始位移量下的阻尼比
3.2 强迫振动条件下结构隔振效果
以45 钢颗粒阻尼器为例,取粒径为4 mm、粒数为1 200,研究颗粒阻尼器在受迫振动时对结构的隔振效果。已知颗粒阻尼器的1 阶固有频率f0=17.453 Hz,由隔振理论可知当(f激励频率,f0:固有频率)时,隔振器具有较高的隔振效率,同时对结构具有良好的耗能效果。因此,对颗粒阻尼器施加频率分别为30 Hz、60 Hz、90 Hz、120 Hz的正弦波激励,对比研究其在强迫振动时对结构的隔振效果。
由图10(a)至图10(d)所示,在一定时程范围内,未添加粒子的颗粒阻尼器的支反力幅值会随着激励频率的增大而减小;特别当频率由图10(a)中频30 Hz 增加到图10(b)高频60 Hz 时,支反力幅值由2 500 N衰减到不足1 000 N,衰减传递率达到40%,可见未添加粒子的颗粒阻尼器具有较好的隔振性能。同时,添加粒子的颗粒阻尼器的支反力幅值也会随着激励频率的增大而减小;当频率由中频30 Hz增加到高频60 Hz时,支反力幅值由1 500 N 衰减到500 N,衰减传递率达66.6%,可得添加粒子的颗粒阻尼器具有更好的隔振性能。
比较图10(a)至图10(d),在相同激励频率工况下,在一定时程范围内,相比于未添加粒子的工况,添加粒子的颗粒阻尼器的支反力幅值衰减更快,可见添加粒子的颗粒阻尼器具有更好的隔振效果,其对结构的振动衰减以及激励振幅的控制起到了良好的作用。以120 Hz为例,未添加粒子的阻尼器的支反力幅值在1.0 s时还未见明显衰减,约为512 N,而添加粒子的阻尼器的支反力幅值仅在0.2 s 时就衰减约为292 N,隔振效果增强43%。
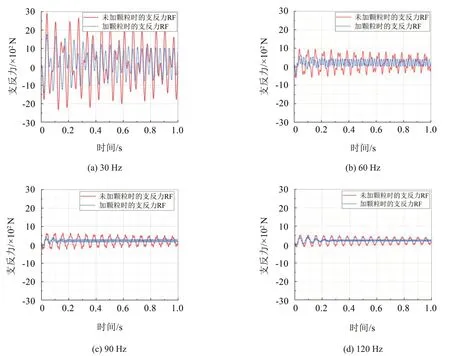
图10 中高频段隔振效果
4 结语
基于离散单元法元和多体动力学建立了颗粒阻尼器碰撞模型,并通过试验对模型的有效性进行了验证;以等效阻尼比为评价指标,研究不同的颗粒材料、粒径、数目、初始位移量各参数变化对颗粒减振器减振性能的影响;同时验证了颗粒阻尼器在耗能的同时,还具有中高频段的隔振效果。具体结论如下:
(1)对于45钢、玻璃、铅3种材料,钢颗粒阻尼效果较佳,且钢颗粒廉价易得。
(2)控制颗粒总质量相同时,粒径越小,阻尼效果越好。
(3)颗粒材料及粒径相同时,颗粒数目是影响颗粒阻尼器减振效果的重要参数且存在最优值,在设计颗粒阻尼器时,应在满足实际工程应用要求的前提下,尽可能增加颗粒数目,以获得更好的颗粒阻尼减振效果。
(4)初始位移量是等效阻尼比的敏感影响因素,且对阻尼比的影响存在临界值。
(5)该颗粒阻尼器不仅有良好的耗能作用,而且对中高频段具有极佳的隔振效果。
