基于Vold-Kalman阶次提取的非平稳声源定位方法

陈剑雨，董广明，陈 进，赵发刚

（1.上海交通大学机械与动力工程学院振动、冲击、噪声研究所，上海200240；2.上海卫星工程研究所，上海200240）

声源识别是旋转机械声源定位、状态监测和故障诊断的重要手段，波束形成作为声源重建的典型方法，适用于远场工况，对高频声场具有良好的重建能力，被广泛应用于生产与生活。针对平稳声信号的波束形成手段众多，且效率很高，近些年来自适应波束成形（Beamforming）[1–2]、主成分分析[3–4]、多重信号分类算法[5]和压缩感知[6–7]等一系列面向波束成形协方差矩阵的主成分提取和噪声去除算法的发展使得波束成形在实际工程场景中的应用更加广泛。但是在面对旋转机械的升速、降速和失速状态所产生的非平稳宽频声信号时波束成形具有一定的局限性，并不能沿用平稳信号的波束成形方法。在处理这种宽频阵列信号时，Valaee 等利用总最小二乘相干信号子空间方法实现宽带信号定位，结果优于旋转子空间算法[8]；Wang 等提出了一种利用单信号子空间高分辨率地估计多重宽带平面波到达角的方法，提供了处理混叠宽带信号波束成形的一个范例[9]；Ward 等采用了一种基于频率不变波束形成的波束空间预处理结构，提出一种新的宽带法场信号到达方向估计方法[10]；Chan 等搭建了一种用于均匀同心圆阵列的具有近频不变(FI)特性的数字波束形成器[11]。Frikel和Bourennane改进了双边相关变换，利用聚焦矩阵只对各频率处估计的信号子空间进行变换，从而得到所有分析波段的相干信号子空间，进而完成声源角定位，但是这种方法的使用范围比较窄，难以在声场信号处理中推广[12]。除此之外，时频分析也是研究非平稳信号的工具[13]，经典的理论有Gabor变换[14]、短时傅里叶变换[15]和小波变换[16]。这些方法在非平稳声源定位问题中具有很好的参考价值，在应对面向旋转机械的非平稳声源信号处理中，Vold-Kalman 阶次追踪方法是一种典型有效的方法[17–20]，其在风机齿轮箱故障诊断[21–22]和旋转轴瞬时特征提取[23]等方面具有良好的应用基础，因此可以引入Vold-Kalman 阶次追踪方法处理旋转机械升速工况，辅助完成波束成形声源识别，在对时域信号进行角域重采样的基础上，对信号进行阶次识别和提取，提取出的特征阶次信号对应于旋转机械的特定声源谐波信号，可以用特征阶次的信号进行非平稳波束成形。本文基于该思路首先对旋转机械线性调频信号的识别定位进行了仿真，在角域中重点研究不同线性调频信号混叠的情况下Vold-Kalman 阶次追踪性能，结合时频分析对不同特征阶比的信号进行对比，提取有效的窄带信号进行波束成形声场重建，然后采用上海机动车检测中心提供的耦合双电机升速试验数据对该方法进行电机定位验证。经过角域推广后的波束成形算法，既能规避宽频下无法进行声源定位的问题，又减少了宽带波束形成庞大的运算量。

1 Vold-Kalman阶次提取

阶次追踪是面向旋转机械非平稳状态的一种有效的分析手段，应用在诸如旋转波动、升降速等情况。阶次追踪方法通常分为硬件式、计算式、无转速计式以及基于Vold-Kalman 滤波器的时域阶次追踪技术。与其他阶次追踪方法相比，Vold-Kalman阶次追踪可以提取多个阶次分量，其解耦临近和交叉阶次的准确性也最好。

为了追踪目标阶次的信号，构建状态方程和观测方程，信号模型用幅值和载波乘积的形式表达，通过求得的包络幅值重构阶次信号。将阶次信号模型表示为幅值和载波的乘积：

式中：k表示阶次，ak(t)表示复包络，θk(t)是载波，ω(τ)是参考轴角频率。

如果Vold-Kalman滤波器提取单个阶次成分，那么观测方程为

x(n)表示测量信号，a(n)θ(n)表示要提取的阶次成分，ξ(n)表示剩余成分，包括其他阶次和噪声。变换成矩阵形式为

为了求解a(n)，需要对非齐次项ξ(n)和ε(n)做一个约束，r表示加权因子，用以平衡两个非齐次项的比例，从而控制它们对结果的影响，这个约束表达为

约束J关于aH1阶导数为零，

式中：r2ATA+E是对称正定矩阵，因此可以进行Cholesky分解，上式化为

先通过向前分解求出z，再通过向后代入求a，由此完成对包含多重分量复杂信号的阶比分量提取。提取出的单个阶比的信号往往可以对应到声场中的局部特征，通过对阶比信号追踪分析，就可以对信号的各个子特征进行识别诊断。本研究主要针对旋转机械声场信号进行分析，Vold-Kalman分解算法包含转速参考，有利于进行时域信号的角域重采样，主要的信号分析流程见图1。

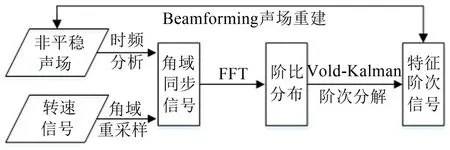
图1 基于Vold-Kalman分解的角域推广波束成形

如图1所示，在引入Vold-Kalman分解处理旋转机械非平稳声源定位问题时，首先要结合旋转机械的实际转速信号进行拟合，提取满足旋转机械完整旋转周期的时域测量时刻序列，辅助应用于声场信号的等角度重采样，即对时域间隔相等的采样信号依据转动角度进行插值，形成转动角度间隔相等的信号序列。对经角域重采样后的数据进行快速傅里叶变换（Fast Fourier Transform，FFT），就可以识别出信号中的各个阶比，利用Vold-Kalman滤波算法提取各阶比的分量信号，结合各阶比信号的时频分析结果观察其声源对应特性，然后选取时频分布上表现良好的阶比信号段进行波束成形，逐个完成声源的识别定位。

2 非平稳信号波束成形仿真

实际的由非平稳信号组成的声场尤其是旋转机械升、降速过程中的振动噪声信号在频域上大多表现为多重线性调频信号的叠加，这里通过在声场仿真中添加线性调频声源模拟实际非平稳信号声场，对这种非平稳信号波束成形算法进行仿真研究。

在仿真中设置两只自由场线性调频声源，见图2(a)中XY平面中黑色圈点标识，在声源面设置等效声源若干，便于构建传感器阵列与声源平面之间的声传播矩阵，如图2(b)所示，为了贴合仿真与后续试验数据算法应用场景，这里引入与后面实际实验中相同的B&K PULSE 数据采集与处理系统，其由36 只用于采集声场信号的传感器组成，传感器阵列设置于等效声源面垂直正上方。

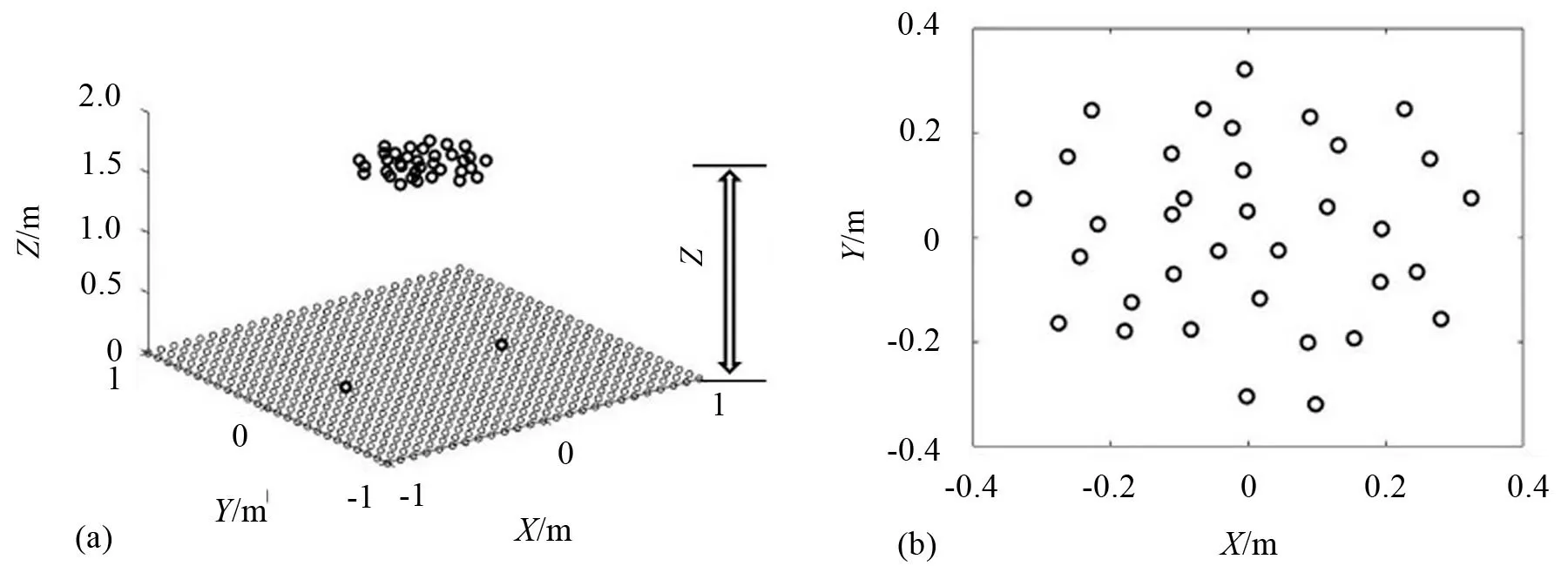
图2 实验布局设置

如表1所示。仿真中采用常见的线性调频信号（chirp），该宽带信号频率范围根据实际仿真需求设置，采样频率为32 768 Hz，为了模拟实际声场环境，仿真中添加高斯背景噪声，信噪比为0。仿真中设置快拍数为32 768，因此信号时间长度为1 s，传感器阵列与声源平面之间的距离设置为1.68 m，与后续实验参数保持一致。

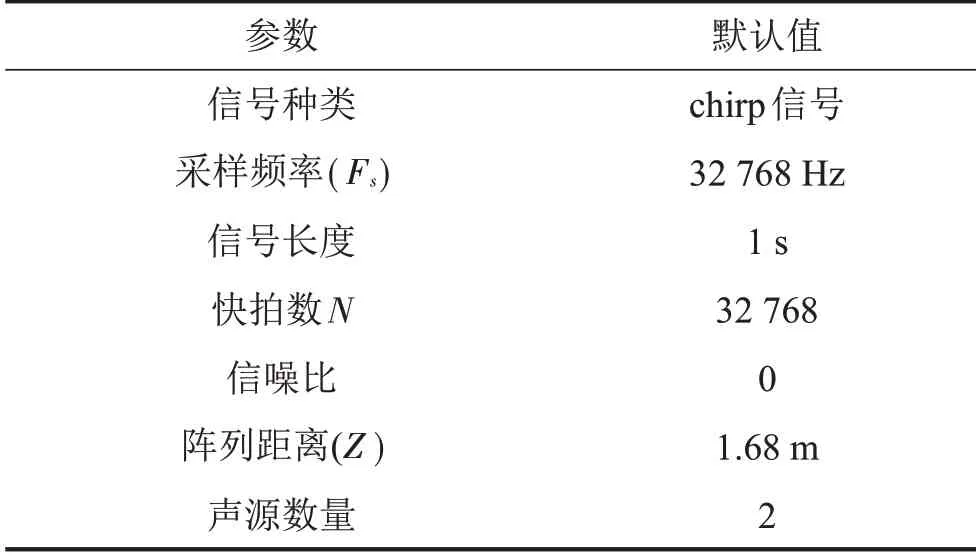
表1 仿真参数设置

为了充分研究非平稳声源波束成形定位方法，共进行3组仿真，基于声源之间不相干的假设，分别研究基本非交叉宽频声源波束成形、交叉多声源波束成形以及多倍频叠加声源定位。在说明宽频线性调频信号波束成形可行性基础上，进行多重线性调频信号声源定位仿真，引入角域推广下基于Vold-Kalman阶次追踪的波束成形方法，在仿真中验证其提取多倍频宽频信号叠加声场中阶次分量的有效性。

在第一组仿真中，如图3(b)所示，设置两个声源的坐标分别为(-0.5 m，0，0)和(0.5 m，0，0)，两个声源频率范围为f1=2 000 Hz～2 500 Hz，f2=2 500 Hz～3000 Hz，为线性增加的非相干声源。如图3(c)至图3(d)所示，仿真中两个不相干的线性调频声源可以在各自的频率范围内分别实现声源定位，说明对于由简单的非相干宽带线性调频声源组成的声场直接进行波束成形就可以完成声源定位。可以看到，当两个声源的频率范围不发生交叉时，在各自对应的频率范围内直接进行波束成形聚焦，就可以分别实现两个声源的定位，因此，即使两个声源的信号为线性相干的调频信号，即两个声源在频域上频率不交叉，而是呈现倍数关系，理论上也可以在各自的频率范围内单独定位，与仿真一呈现的结果类似，这里不再展示。

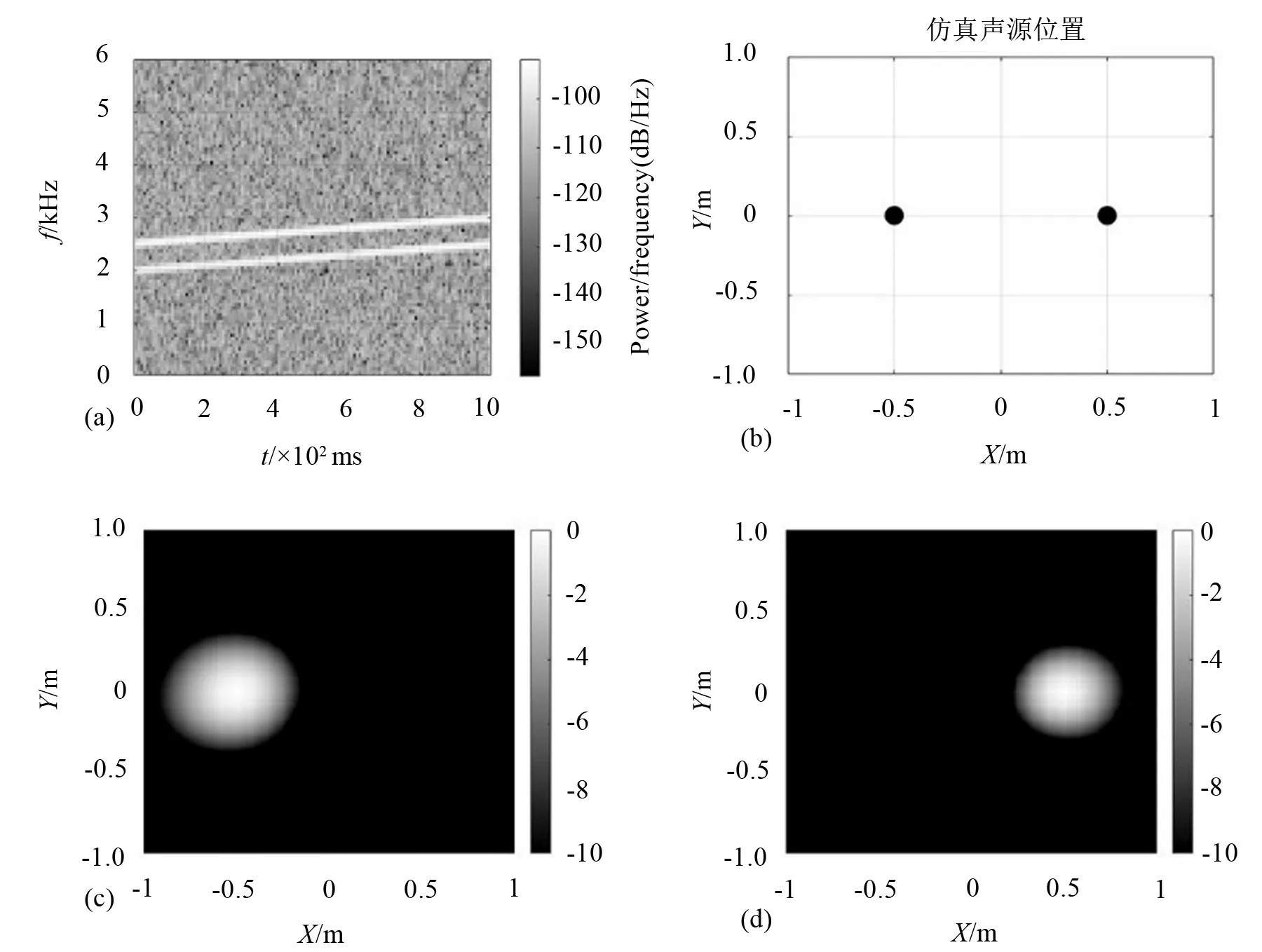
图3 非相干声源仿真

如图4 所示。在第二组仿真中，共设置3 个声源，分别设置频率范围为f1=2 000 Hz～2 500 Hz、f2=2 000 Hz～2 500 Hz线性增加以及f3=2 000 Hz～3000 Hz 线性减少，3 个声源的位置见图4(b)中红圈标识。这种情况更接近于实际实验中的声场信号，可以看出，此时声源识别效果较差，当这里的声信号属于基本的交叉声源情况时，虽然声源依然是非相干声源，但是声场重建声源数目不准确，明显次级亮点较多，影响结果分析，对于这种交叉非相干声源的情况需要对信号进行进一步处理。

图4 频率交叉声源仿真

旋转机械产生的非平稳声场信号除了会发生仿真二中所描述的信号在频率上交叉的情况之外，还会有由于旋转机械本身的旋转运动特性而产生的大量的基于转速的倍频信号，这些信号虽然不会出现明显的频率交叉，但却是互相相干的信号。在仿真三中对这种相干声源进行研究。因此，对于实际应用中的更为复杂的声场信号，如多重信号相叠加的情况，则必须考虑引入Vold-Kalman 阶次追踪，提取出单一阶次的信号，再进行声源识别，从而提高声场声源识别的有效性。

在图5 所示仿真中，设定4 组线性调频信号，频率范围分别为f1=1000 Hz～1500 Hz、f2=2 000 Hz～3000 Hz 、f3=600 Hz ～800 Hz 、f4=1800 Hz ～2 400 Hz，其中f2=2f1，f4=2f3。在仿真中将频率范围对应于f1和f2的线性调频信号叠加于声源一，将频率范围对应于f3和f4的线性调频信号叠加于声源二，由此，两个声源包含的基频信号不相干，但对于单个声源来说，其包含了线性相关的两只信号，以此模拟在旋转机械声场中出现的多倍频信号。仿真中采集到的声场信号如图5(a)所示，共包含对应两组基频的4 支信号，如果直接对该声场信号进行窄带波束成形，结果如图5(b)所示，声场重建结果在全频率内出现混乱，无法得到有效的声场重建从而完成声源定位。因此对仿真信号进行角域重采样，然后进行傅里叶变换后得到阶比分布，包含两个阶比：1.57和5.47，利用Vold-Kalman滤波提取各阶比的分量，即得到对应于单个声源的声场信号。两个阶比下的声场信号的声场重建结果如图5(c)至图5（d)所示，可以看到，对不同阶比的信号进行波束成形实现了两个声源的定位，与仿真设置一致，且声场重建结果远远优于图5(b)所示对复杂信号直接波束成形所得结果。

图5 相干信号叠加声源仿真

综合信号非相干声源、信号频率交叉声源和相干信号叠加声源3 组仿真结果可以发现：当信号在频域上不发生交叉时，无论信号是否线性相干，都可以通过时频分析选取不同频率范围对声源直接进行逐个定位；当声场中包含的多组宽带信号出现频率交叉时，在声场重建中需要考虑不同的频率选择，且由于各频率信号幅值和相位可能是由多个声源信号叠加而得到，最终的波束成形结果往往出现较大的偏差，即声源识别位置不准确、声源缺失和出现次级声源亮点，从而影响声场中声源的定位；当采集到的信号包含来自于不同声源即不同基频信号倍频成分时，声场中各信号频率范围发生交叉，且不同声源发出信号包含多个特定基频的宽带倍频分量，这时采用Vold-Kalman方法可以有效地识别基频和倍频，提取出对应于不同声源信号的阶次信号，通过对相应阶次信号进行波束成形即可得到该特定声源的重建定位。因此，这种基于Vold-Kalman分解的角域推广波束成形方法对宽带非平稳声源定位具有良好的仿真适用性。

3 电机声源定位实验

电机升速实验在半消音室内进行，使用永磁同步电机与测功机对拖，如图6 所示。其中电机的额定功率为15 kW，额定电压为115 V，最高转速为7 300 r/min。实验测量与分析中使用B&K PULSE数据采集与处理系统，共包含36只传感器，传感器阵列正对被测电机平面，垂直距离为1.68 m，采样频率fs为32 768 Hz，为了便于分析实验数据，实验中使用电涡流传感器记录对拖轴的周向转动次数，可以用于转速分析和等角度采样参考。从图6(b)中可以看到由传感器阵列采集到的非平稳声源呈现为具有一定尺寸的周向混叠区域，在其他相当多的频率段，声场重建结果甚至直接呈现为无规则混乱状态，难以分辨声源，所以直接处理声场信号难以完成有效的声源定位，需要对声源信号预先进行阶次提取。

图6 实验设置

首先对电机升速过程中采集到的转速脉冲序列进行转速估计，得到电机升速过程中的转速记录，如图7(a)所示，整个数据记录过程中电机的转频从32 Hz线性升高到87 Hz，然后根据转速-时间离散曲线对时域信号进行等转动角度重采样，从图7(b)中可以看到完成角域重采样之后的数据长度比原等时间间隔序列长，这是因为角域重采样是根据采样频率以最低转速确定插值长度，随着转速增大，单个时间间隔转动角度增大，因此需要插入更多的等角度序列。从图7(c)中可以看到，实验信号为混合多重线性调频信号的复杂声场信号，在较低频率处信号能量较大，在高频率处能量有限。对经重采样后的信号进行傅里叶变换就可以得到阶次分布，通过提取各个阶次的信号，可以得到独立的阶次分量，从而用于声源定位。可以看到，在图7(d)所展示的阶比分布中存在大约10 个不同的阶比，从Vold-Kalman 分解的原理来看，这些阶次本质上对应旋转机械电机的倍频信号，因而各阶次代数值为某基本阶次代数值的整数倍。从实验电机和测功机工作过程来看，噪声主要来自于装备旋转运动所产生的振动，不同倍频信号对应不同的电机结构和工作状态，这里结合实际时频分析的结果，选取几个具有代表性的幅值较大的阶次（3.59和16.85）进行信号提取。

图7 基于Vold-Kalman阶次提取前处理

利用Vold-Kalman 阶次追踪方法提取出特征阶次的信号，并在时频分析结果中找到结果比较好的频率窄带进行波束成形。如图8(c)所示，对实验信号直接进行波束成形，根据声场重建结果无法直接识别声源，因此根据时频分析结果提取阶次3.59 和16.85，对应这两个阶比提取出的信号中包含对应于两个设备的噪声分量。利用该组阶次下提取出的信号分别进行波束成形可以定位两个声源，将两个声场重建的结果合并到一张图里如图8(d)所示，可以直观看到两个声源的位置，可以看到在重建面上两个声源的坐标分别为（-0.5 m，0）和（0.5 m，0），这与实验中电机与测功机的位置坐标一致。结合仿真结果和实验电机定位结果可以证明这种方法对于非平稳声场信号处理具有良好的可行性，与此同时，其除了可以识别声源，还可以有效重建声场，完成较高精度的声源定位。

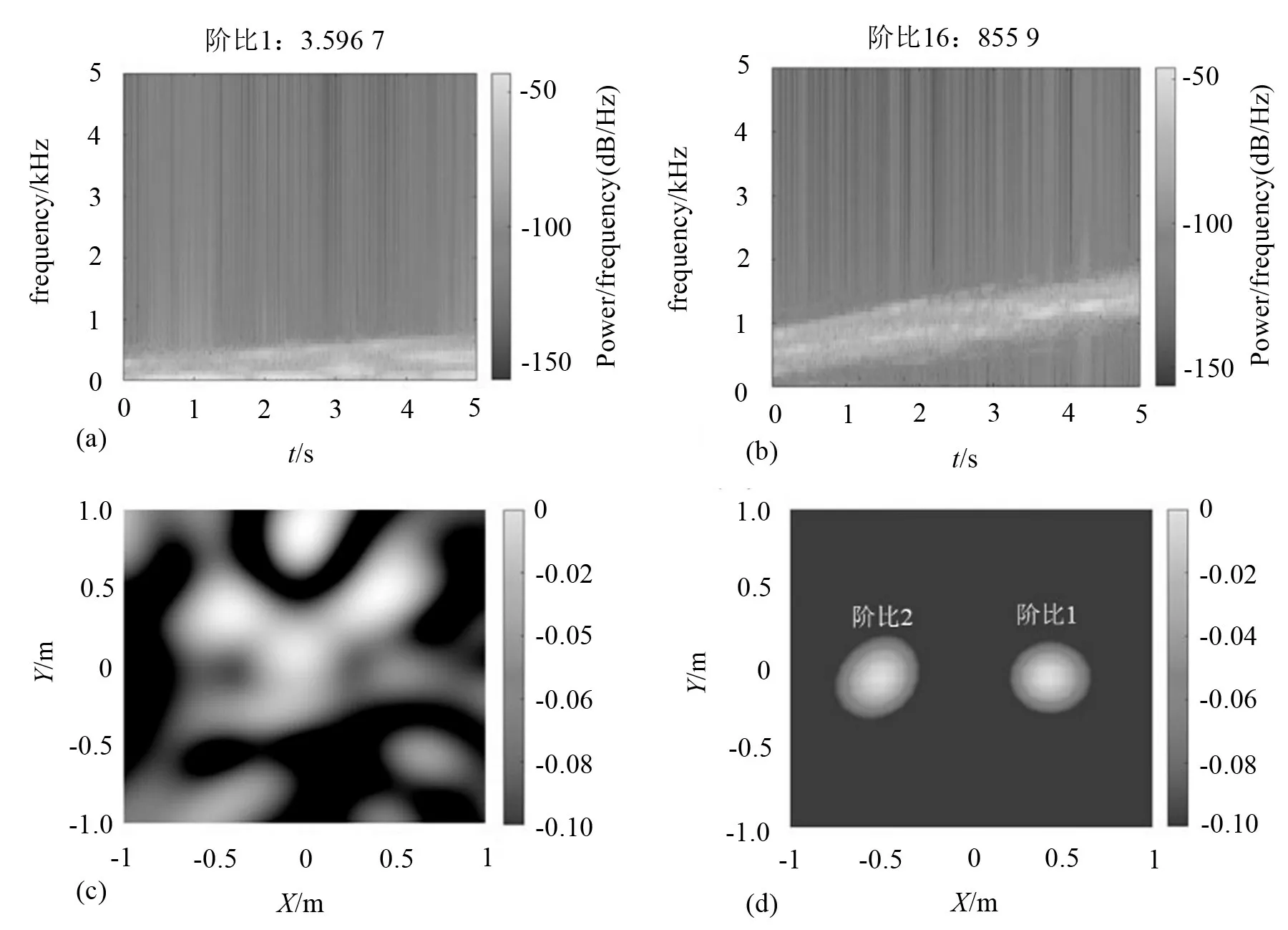
图8 特定阶次信号波束成形结果

4 结语

在处理非平稳旋转机械声源识别或故障诊断时，可以利用转速信息对声场复杂信号进行等转角重采样，再利用Vold-Kalman滤波提取信号特征阶次的信号，然后进行波束成形。在这种方案中，一方面通过Vold-Kalman 滤波在从复杂混乱的信号中提取出特定阶次信号的同时可以去除一定的噪声，另一方面在对提取出的信号时频分析中可以直观地看到相对平稳的频率段，经过这两步处理过程，就可以使用一般的波束成形完成声源识别。本文针对非平稳旋转机械声场成像，通过引入Vold-Kalman 阶次分解，提取出对应于声源的有效谐波信号，通过基本的声源识别、定位仿真和实验验证了这种方法的有效性。结果表明这种方法在旋转机械故障诊断中有较大的应用潜力，如进行局部声源定位、进行故障位置诊断。如果进行进一步的自适应阶比选取算法开发，还可以以本文提出的方法作为基础进一步研究实时声源位置跟踪。因此这种方法在非平稳声源识别和旋转机械状态监测等领域具有相当大的应用潜力。