基于Triple GAN的滚动轴承故障诊断方法研究

2021-08-21胡兵兵唐嘉辉武吉梅

噪声与振动控制 2021年4期

胡兵兵，唐嘉辉，武吉梅，刘杰

（1.西安理工大学印刷包装与数字媒体学院，西安710054；2.西安理工大学机械与精密仪器工程学院，西安710048）

滚动轴承是旋转设备中的重要部件之一，其运行状况好坏会影响整个设备的稳定性[1]。因此，滚动轴承的状态监测与故障诊断对于保证机械设备平稳运行有着十分重要的意义[2]。传统滚动轴承故障诊断方法主要包括两个步骤，首先使用传感器等采集设备收集轴承振动信号，然后通过一系列以信号处理为基础的方法提取故障特征，从而达到故障诊断的目的。但此类分析方法对于信号处理算法以及专业知识有较高的要求，同时故障程度不同或现场工况复杂等情况会导致所采集到的振动信号信噪比较低，难以达到高精度故障诊断的目的[3–5]。

随着人工智能算法的逐步发展，其在故障诊断领域的应用也受到了学者们广泛的关注。目前基于机器学习或深度学习算法的故障诊断方法主要分为以下两步：首先通过算法模型从原始数据中提取故障特征，之后将特征输入至指定分类器进行分类，从而达到判定故障类型的目的[6–8]。

Tamilselvan等[9]结合多传感器信息，将深度置信网络应用在航空发动机故障诊断中，并取得了较高的准确率。Wen等[10]提出了一种基于卷积神经网络的机械故障诊断方法，该方法将振动信号转换为二维图像后，再经过卷积神经网络自动提取特征，消除了人为提取特征对结果的影响，相比于传统故障诊断方法在诊断精度方面有了显著的提升。但上述方法在训练模型的过程中需要大量的带有标签的数据，而在实际工况条件下，较难获取带有标签的机器运行数据[11–12]。徐林等[13]结合连续小波与改进的生成式对抗网络(Generative adversarial nets，GAN)各自的优点，提出了一种应用于滚动轴承故障诊断的新方法，在缺少样本数据的情况下取得了较高的诊断准确率，但此方法中训练GAN模型时无法同时保证生成器与判别器达到最优，并且仅对输入模型的数据进行了评估而未考虑标签的作用。针对上述问题，本文提出了一种基于三重生成式对抗网络(Triple generative adversarial nets，Triple GAN)的滚动轴承故障诊断改进方法，该方法在传统GAN的基础上通过引入分类器克服了传统GAN 模型中生成器与判别器无法同时取得最优解的缺点，并在标签数据不足的情况下，实现了高准确率分类以及数据标注。同时，借助具有广泛搜索域及高效率搜索等优势的量子遗传算法实现了Triple GAN网络模型中的学习率等参数的自适应寻优，避免了人为设置参数时所致费时费力。本文所提方法有效解决了目前传统智能故障诊断方法标签数据难以获取、训练参数较难设置等问题，为滚动轴承的故障诊断提供了一种新的研究思路。

1 基本理论

1.1 Triple GAN理论

传统GAN 网络模型训练过程可以理解为是一个根据两人博弈理论经过迭代后输出一个类似于真实分布的伪样本的过程。其中生成器是以噪声信号作为输入，判别器是用来判断输入样本来自于真实分布还是伪分布。上述过程一直持续循环至模型达到动态平衡为止，即生成样本无限接近于真实分布，且判别器无法判断输入样本是否来自于真实样本分布。整个训练过程可以定义为一个最大最小值问题[14]。

其中：Pdata(x)是真实数据的分布，而Pz(z)是噪声分布（常被定义为正态分布或者均匀分布），G(z)是由噪声Z生成的样本。

由于传统GAN 网络模型的核心是两人博弈理论，使得生成器与判别器不能同时达到最优。并且网络模型在训练过程中仅评估数据而忽略了已有标签的作用，同时网络模型中的单个判别器也无法完成生成样本与预测标签两项难以兼容的工作。为了解决此问题，2017年Li 等[15]提出了Triple GAN 模型。对于一个仅存在部分标记样本的数据集，Triple GAN 主要有3 个部分组成，两个条件网络分别对应生成器与分类器，生成器的作用是通过真实标签生成伪样本，而分类器是根据真实样本生成伪标签，仅有的一个判别器被用来判断来自两个条件网络的样本联合分布的真伪。该过程可以定义为

其中：(x,y)是样本标签数据，α是用来衡量分类与生成平衡性的权重参数。通过引入交叉熵损失，可以保证模型性能达到全局最优，其网络模型主要结构如图1所示。

图1 Triple GAN结构示意图

图1中C、D、G分别为分类器、判别器与生成器，p(X,Y)为真实样本分布，p(z)为噪声分布，“CE”为监督学习产生的交叉熵损失。“A/R”分别表示接受与拒绝所产生的对抗损失。对抗损失与无偏正则化的共同作用使得生成器产生的分布pg、分类器产生的分布pc与真实数据分布p保持一致。

传统的GAN 模型在故障数据生成方面表现优异，而在故障分类及数据标注等方面表现较弱。Triple GAN 模型则是继承了传统GAN 模型优越的故障数据生成能力，并通过引入分类器将传统GAN忽略的标签信息平滑输入至模型数据空间中，利用参数调节最终实现网络的动态平衡。基于以上描述，利用Triple GAN 模型实现轴承故障诊断的主要过程可简述为：用分类器对采集到的轴承振动时域信号进行迭代训练并输出伪标签，同时在已有故障标签的指导下，通过生成器对噪声信号进行迭代训练，输出与真实样本具有同属性的伪样本。通过判别器对输出的伪样本与伪标签进行比较，从而实现生成器与分类器参数的动态调整，以得到用于轴承故障类别判断的网络模型。

1.2 量子遗传算法

量子遗传算法是在传统遗传算法的基础上，引入量子比特编码与量子旋转门对种群进行编码与更替，以实现降低种群规模，从而达到加快寻优速度、更快速准确求出最优解的一种智能优化算法[16–17]。此算法的核心特点之一是使用量子态对种群进行编码。由于量子比特存在两种表达状态和其中表示自旋向下的状态，而表示自旋向上的状态[18]。故每一个量子位均可由这两种状态进行表示，可表示为

两种状态的复数域振幅α和β满足1的关系，其中 |α|2与 |β|2为对应状态的概率值。经典的信息理论常用双比特表示信息，对应有00，01，10，11 4 种状态，对应的4 种量子态分别为和。

为了实现种群更新，量子遗传算法中常采用满足归一化条件的酉变换使量子门对量子态进行一定角度的旋转来实现。旋转门可将量子态旋转θ角度，旋转门的作用过程如下：

量子遗传算法中所使用的适应度函数与传统遗传算法无明显区别，其作用都是求出适应度值以衡量个体是否遗传。一般情况下，适应度值越大则代表该个体更接近最优解[19]。量子遗传算法的具体流程如图2所示。

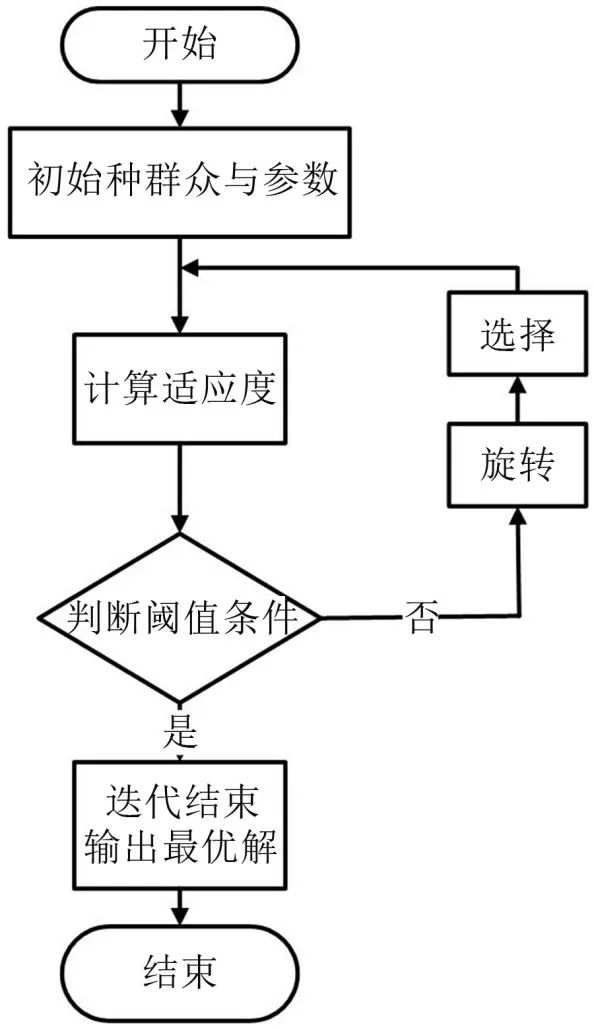
图2 量子遗传算法流程图

2 基于量子遗传优化算法的Triple GAN轴承故障诊断方法

由于Triple GAN模型中生成器与分类器的学习率对模型的训练效果至关重要，且此模型对学习率的初始值非常敏感，而基于该模型的诊断准确率与学习率之间又缺少直接的线性关系，人为设置学习率易导致模型收敛速度缓慢。为了解决该问题，本文通过引入量子遗传算法，利用其广泛的搜索域及高效的搜索效率，有效实现了Triple GAN 模型的学习率寻优问题。Triple GAN模型的学习率主要由生成器学习率与分类器学习率两部分组成。本文所采用的适应度函数如下：

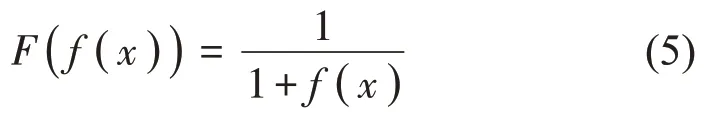
其中f(x)为网络模型的误差函数。

基于引入量子遗传算法后的Triple GAN模型轴承故障诊断方法的主要步骤如下：

（1）采集轴承振动信号，将数据截取至指定维数构成原始样本集。

（2）初始化量子遗传算法的种群个体，设置种群个数N=20，最大迭代次数T=200。

（3）将单个个体对应的参数值输入Triple GAN模型，完成训练，输出结果。

（4）计算种群个体对应的适应度值，保存最优个体及其适应度值，并判断是否满足阈值条件。若满足则进行下一步，不满足则利用量子旋转门更新种群，重新选择种群个体，返回步骤（3），直至满足阈值条件为止。

（5）将满足阈值条件的解转换为二进制编码，再转换为学习率的最优解。

（6）将最优解输入模型完成最终训练，输出诊断结果。

量子遗传算法中收敛至最优种群所使用的旋转角一般是固定的，通用的旋转角选择策略如表1 所示。第j旋转角由旋转角度θ和旋转方向s(αj βj)组成。选取旋转角的方式是通过将现有个体的适应度值f(x)与当前最优目标值f(best )进行对比，若最优目标适应值更大时，则调整旋转角使现有个体向besti靠近。旋转角度θ的大小对模型收敛效率影响较大，过大会导致无法收敛，过小会导致无法取得全局最优解，根据以往研究经验本文选择旋转角度为0.01π。利用量子遗传算法可将Triple GAN 模型中学习率初始值优化至最优解附近，使Triple GAN 模型能更快速准确进行样本数据分类与标注。

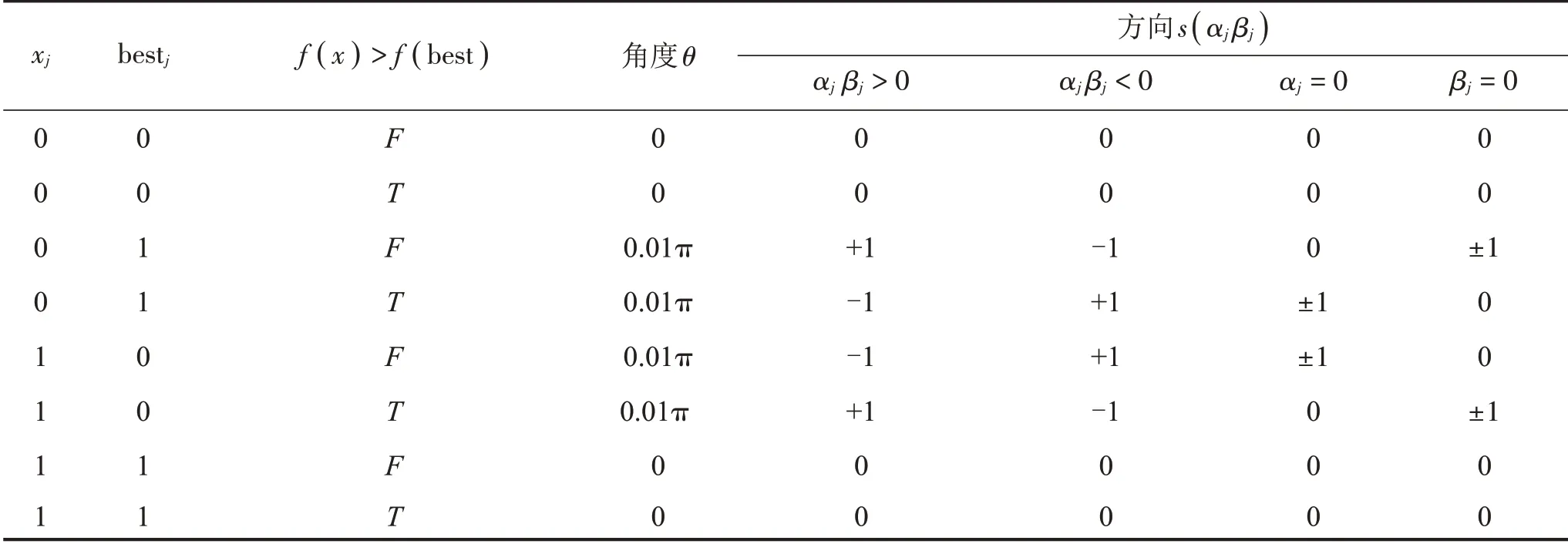
表1 旋转角选择策略

3 实验验证

为了验证基于Triple GAN的滚动轴承故障诊断方法的有效性，本节利用该方法对两种不同的轴承故障数据集进行故障诊断。实验一采用美国西储大学轴承数据集（Case Western Reserve University，CWRU）[20]作为研究对象，对所提故障诊断方法的有效性进行验证。选用具有内圈故障、外圈故障、滚动体故障和正常状态4 种类型的轴承作为实验对象。在4 种不同运行转速工况下（分别为1 797 r/min、1 772 r/min、1 750 r/min 和1 730 r/min）进行信号采集，采样频率为12 kHz。实验二采用德国帕德伯恩大学[21]提供的数据集对本文方法中的参数优化性能进行测试。选用正常状态以及5种人为损坏的轴承作为实验对象。每种轴承均在900 r/min 和1 500 r/min 两种转速工况下进行测试，采样频率为64 kHz。

3.1 实验一

实验一数据集如表2所示，采用长度为1 024的窗函数对原始数据进行截断处理，轴承故障深度分别为0.18 mm、0.36 mm、0.53 mm，用来模拟轴承不同程度的损伤。图3 所示分别为正常轴承、内圈故障轴承、外圈故障轴承和滚动体故障轴承的振动信号时域示意图。

表2 滚动轴承实验数据集

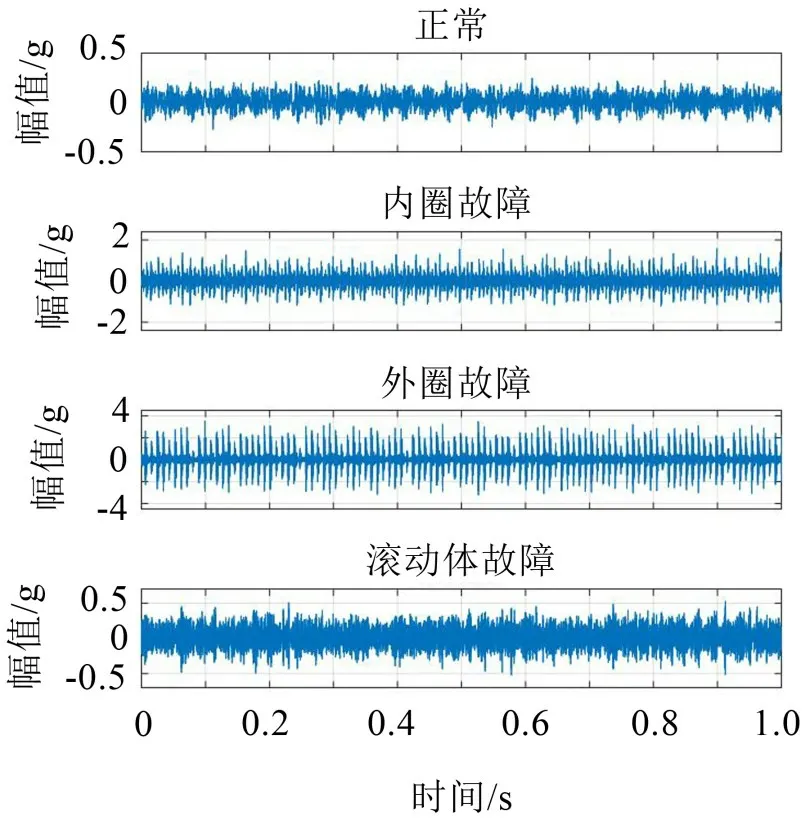
图3 轴承振动信号时域图

从图中可以看出，虽然不同类型故障的振动信号具有各自的特点，但很难观察到隐藏在振动信号中的故障特征。表3所示为实验数据集中含有的标签数据与无标签数据的数量。从表中可以看出该组数据中无标签数据量远超过标签数据，并且标签数据也少于一般机器学习所使用的数据量。因此，使用该组数据可以验证本文所提方法的数据标记能力与故障分类能力。

表3 滚动轴承数据集分配比例

为了验证本文方法的有效性，在实验过程中使用传统生成式对抗网络与支持向量机(SupportVector Machine，SVM)相结合的方法、卷积神经网络（Convolutional Neural Networks，CNN）、深度置信网络（Deep belief network，DBN）、人工神经元网络（Multi-Layer Perceptron，MLP）与经经典量子遗传算法优化后的Triple GAN 作对比。此外，本文采用的数据与对比方法中的数据均为原始时域信号，为了避免偶然结果的影响，每种方法使用相同的参数进行5 次实验，表4 中所示为实验结果。其中Triple GAN模型中的生成器、分类器、判别器均采用卷积层实现。输入噪声采用高斯白噪声，输入维数为100，原始样本维数为1 024，最大迭代次数为1 000。深度置信网络所使用的参数学习率为0.01，最大训练次数为1 000，模型结构为[1 024，800，500，200，10]。卷积神经网络中包含两个卷积层、两个池化层、一个全连接层，使用Softmax 作为分类器，卷积层的激活函数选择为Relu函数，对于池化层选择最大池化法。对于人工神经元网络选择Relu 函数作为激活函数，学习率为0.001，用于衡量轴承故障与正常状态数据之间的可分性。

表4 实验结果

而传统对抗网络方法中的相关超参数选择如下：学习率为0.002，迭代次数为2 000，噪声维数为100，原始样本维数为1 024，对于支持向量机选择高斯核函数，核函数系数设置为0.02，惩罚系数设置为10。

图4 为5 种方法经过5 次重复实验的详细对比结果。从图中可以看出，本文所提方法在5 次实验中均具有较高的准确率，并且相较于其他算法具有更好的稳定性。

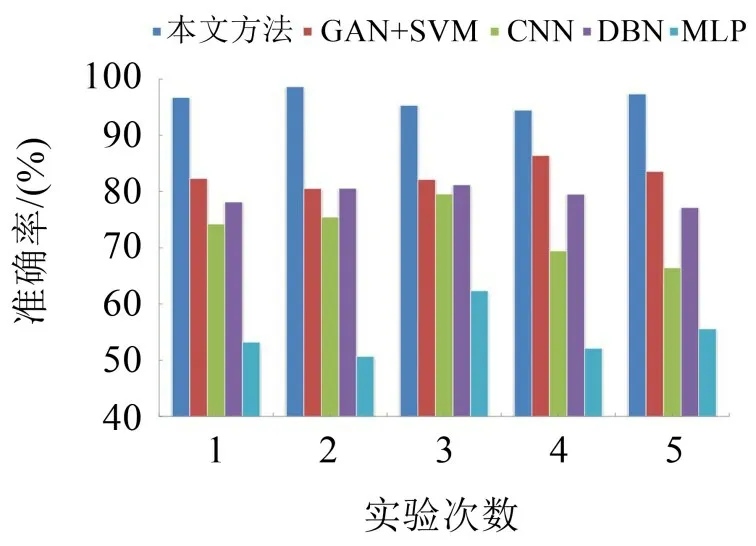
图4 5种方法实验详细结果（5次）

图5为本文方法实验诊断准确率与实验进度关系图，从图中可以看出随着实验的进行，模型被反复训练，不同故障的平均诊断精度逐步提高。

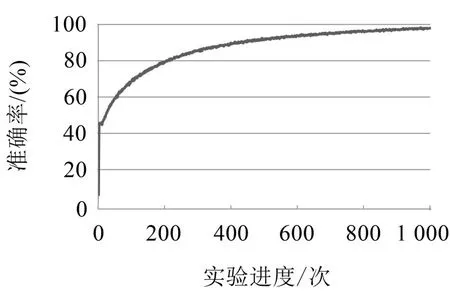
图5 诊断准确率与实验进度关系图

从表4 中的实验结果可以看出，本文所提方法的平均准确率能达到97.37 %，略高于DBN 与GAN+SVM 的平均准确率79.56%和85.58%，明显高于CNN与MLP的平均准确率73.03%和54.78%。本文方法均方差为1.47，明显低于其他4种对比方法（3.32，3.11，2.52，4.10）。该实验结果表明，相较于传统方法，本文提出的方法在处理具有大量未标记数据时具有更高的诊断准确率和较好的稳定性。表5为基于本文方法进行数据标记后的性能测试结果，该实验从总样本中随机抽取6 600个样本，去掉标签后作为原始未标记样本。经过模型训练后，其中6 354个样本被正确标记，准确率为96.67%，未正确标记的标签包含49个内圈故障、61个外圈故障、127个滚动体故障和9 个正常状态。该实验结果表明，本文所提方法能较好地完成数据的标记工作，但对于较为复杂的振动数据，例如对于外圈故障以及滚动体故障进行标注时，准确率仍存在一些提升空间。

表5 样本标记结果

3.2 实验二

实验二数据集如表6 所示。采用长度为1 024的窗函数对德国帕德伯恩大学的数据进行截断处理。

表6 滚动轴承实验数据集

表7所示为选用原始Triple GAN和本文所提方法处理后的5次实验结果。其中原始Triple GAN中生成器与分类器学习率均设置为0.01，而在本文方法中，经量子遗传算法反复寻优之后，最终得到使生成器达到最优的学习率为0.001 6，分类器最优的学习率为0.001 2。从表中可以看出，本文方法实验结果诊断准确率较高，5次实验平均准确率为98.49%，高于传统Triple GAN 的平均准确率89.92%。并且本文方法的平均运行时间为976.2 s，相较于传统Triple GAN 的运行时间（1 196 s）也具有一定优势。通过此实验结果可以看出，基于量子遗传算法对Triple GAN学习率进行优化使该模型在进行故障诊断时具有更高的诊断效率。

表7 对比实验结果

上述两种实验的结果表明，本文方法中的分类器和生成器通过共享标签与样本，基于三人博弈论实现各自最优，弥补了传统生成网络的不足。同时分类器能对未标记的数据进行标记，生成器能准确产生具有轴承故障特征的伪样本，提高了故障诊断的效率。此外，利用量子遗传算法可以对网络模型学习率进行快速、准确寻优，确保了该模型具有较高的诊断准确率与良好的稳定性。