一种基于EMDFICA-CNN的滚动轴承故障诊断方法

2021-08-21王文青李光鑫张建军

噪声与振动控制 2021年4期

王文青，李光鑫，陈勇，张建军，刘睿

（1.河北工业大学天津市新能源汽车动力传动与安全技术重点实验室，天津300130；2.河北工业大学机械工程学院，天津300130）

随着大数据和人工智能在工业制造中的快速发展和普及，如何对制造装备中的关键部件进行状态实时监测(Real-time condition monitoring，RCM) 成为研究热点。工业制造装备大多由旋转机械组成，而滚动轴承作为旋转机械的关键零件，往往安装在关键的旋转部位，需要精准安装定位，不便经常拆卸，因此对其运转进行RCM，有利于及时控制和调整设备工作状态，从而保护其它零部件，延长设备的服役寿命。研究表明：30%的旋转机械故障和40%的电机故障与滚动轴承有关[1]。由于旋转机械振动信号多为非线性不平稳信号以及机械在运转过程中通常伴有不同程度的噪声，如何准确提取故障特征，建立高效的滚动轴承故障诊断体系成为许多科研人员的新目标。

卷积神经网络(CNN)成功应用于手写字体识别之后，研究人员尝试将其应用于其他方面，如自然语言处理[2-3]、医学影像识别[4]、人群密度估计[5]、车辆识别[6]等,取得了一些研究成果。除此之外，研究人员把CNN应用在滚动轴承的故障诊断中，利用其强大的学习能力，将信号处理方法与CNN相结合进行特征提取，实现故障分类、诊断。

王海龙等[7]将EMD与原始振动信号相结合构成二维特征图，实现轴承的故障诊断。Niu 等[8]利用EMD 分解、循环平稳、谱峰度和两相测试样本稀疏表示的故障诊断方法，实现了电机轴承故障诊断。Abdelkader等[9]提出了一种改进的EMD分解去噪方法提取故障信号，从而更好地完成滚动轴承的早期检测和诊断。Lin[10]等比较了多重分形去趋势波动分析、EMD 和小波变换（Wavelet transform，WT）分别与神经网络、马氏距离决策规划以及支持向量机(Support vector machine，SVM)结合的方法，对齿轮箱故障诊断的几种典型组合方法进行评价。

随着独立成分分析(ICA)在信号处理方面不断得到应用，研究人员将其与故障诊断相结合，取得一定成果。田立勇等[11]使用局部均值分解与快速独立成分分析(FICA)相结合的方法，解决了潜水泵故障诊断与分析时的信号干扰问题。Chen等[12]利用ICA和支持向量机(SVM)分别对正常和故障状态下的源信号进行分析实现了装载机变速箱的故障分类与识别。吕跃刚等[13]提出一种基于经验小波变换和ICA联合降噪的方法，解决了强背景噪声下提取非平稳振动信号的微弱故障特征时，系统信号和干扰噪声在频带互相混叠难以分离的问题。为解决低信噪比条件下轴承故障特征提取问题，刘朋等[14]提出一种基于FICA与信息融合的滚动轴承故障诊断方法。

为了自适应地从原始数据中学习判别特征，Li等[15]考虑了一种利用BP 神经网络(Back propagation neural network，BPNN)对滚动轴承进行故障诊断的多尺度局部区域特征学习方法。为解决端到端的故障诊断问题，Wu等[16]采用一种直接从原始振动信号中学习特征的CNN进行故障诊断。Qiu等[17]利用特征提取和深度卷积神经网络(Deep convolution neural network，DCNN)相结合的方法实现了齿轮箱故障的智能诊断。陈仁祥等[18]针对滚动轴承故障诊断时频特征自适应提取与智能诊断问题，提出了一种基于CNN 和离散小波变换的故障诊断方法。为了满足故障诊断及时性的要求，Zhang等[19]将采集的轴承振动信号转化为二维图像，利用CNN完成特征提取和故障诊断。为避免信息丢失，同时得到不同类型的故障，Wang等[20]研究了一种基于多传感器数据融合与瓶颈层优化的CNN。

目前采用的滚动轴承故障诊断方法主要存在以下问题：

（1）采用的原始数据预处理方法所提取的特征不够明显，使得模型学习能力变差。

（2）采用层数较少的CNN模型，诊断精度不高，模型鲁棒性差。若采用层数较多的模型结构，虽然提高了诊断精度，但会导致网络参数增加，结构复杂。

针对以上问题，提出一种基于EMDFICA-CNN故障诊断方法，首先，通过对原始振动信号进行EMD分解，对获得的IMF分量进行FICA分析，准确提取故障特征，便于CNN 进行学习；其次，对CNN模型进行优化，令第二层池化层卷积核为1；最后，结合softmax 分类器识别不同故障类型。在简化模型结构的同时解决了浅层网络结构学习能力差、诊断精度低的问题。

1 EMDFICA-CNN模型介绍

1.1 EMD基本原理

EMD 是Huang 于1998年提出的一种新型自适应信号时频处理方法，被认为是以傅立叶变换为基础的线性和稳态频谱分析的一个新突破[21]。胡茑庆等[22]利用EMD 分解获取不同状态下太阳轮振动信号的前8个IMF分量，选择前6个峭度较大的分量作为有效IMF，之后利用6 个IMF 分量创建数据集并划分训练集和测试集，并将其输入到DCNN 模型中得出诊断结果。

由于实验中所采集信号通常含有不同程度的噪声，传统的EMD 分解会造成原始信号的模态混叠，产生一些虚假分量，若选取不当，将对最终的诊断结果造成影响。

对采集的振动信号采用EMDFICA 的处理方法，首先对信号进行EMD 分解，其本征模函数需满足以下两个条件：

(1)在整个时间范围内，函数的局部极值点和过零点的数目必须相等，或最多相差一个；

(2)在任意时刻点，局部最大值的包络（上包络线）和局部最小值的包络（下包络线）平均值必须为零。

若振动信号满足上述条件，则按照以下步骤对其进行EMD分解：

（1）当确定x(t) 所有局部极值点后，将所有的局部极大值点和局部极小值点用三次样条曲线连接起来，形成上包络线和下包络线。

（2）计算上下包络线的平均值m1，令：

判断h1是否满足IMF 的条件，若满足，则h1为x(t)的第一个IMF分量。

（3）若h1不满足IMF 的条件，则把h1作为原始数据，重复步骤（1）和步骤（2）k(k=1,2,…)次，直到h1k=h1(k-1)-m1k满足IMF的条件（其中m1k为第k次重复过程中上下包络线的平均值）。记c1=h1k，此时c1为信号x(t)的第一个分量。

（4）将c1从x(t)中分离出来，得到：

将r1作为原始数据重复步骤（1）至（3）得到x(t)的第2个IMF分量c2，重复循环n次，得到n个IMF分量。于是有：

当满足预设的终止条件（常设定的终止条件为rn成为一个单调函数，不能再从中提取满足IMF 条件分量）时，循环结束。这样由式（2）和式（3）得到：

式中：rn为残余函数，表征信号的平均趋势。

1.2 快速独立成分分析

对于1.1 节中获得的分量IMF1、IMF2、…、IMFn，有的分量中仍然含有噪声，使得中低频高能量噪声掩盖了原始信号，无法得到独立源信号。此时引入FICA，对得到的IMF分量再次进行分离。

假设此时的每个IMF 为一个混合信号，即h1、h2、...、hk。

假设存在一组独立的源信号S(t)，使得S(t)=一组观测信号W1(t)=中的各分量由S(t)中各独立信号源组合而成，可用如下矩阵表示：

式中：W1(t)为观测矩阵，A为一个未知的满秩m×n(m≥n)混合系数矩阵，S(t)为信号源矩阵。当S(t)和A都未知时，利用FICA，通过统计学获得分离矩阵M，使分离矩阵满足：

式中：Yt=[y1(t),y2(t),…,yn(t)]T是源信号S(t)的估计。采用这种预处理方法，直到得到组成混合振动信号的独立信号源分量，选取前6 个分量组成样本集。

1.3 CNN模型介绍

CNN 是一种典型的前馈神经网络，由卷积层、池化层、全连接层和输出层组成。

卷积层：卷积层的作用是通过不同的卷积核进行卷积操作，卷积核是一个矩阵（或张量），又称为卷积滤波器。利用不同尺寸的卷积核获得不同大小的感受野，通过激活函数得到输出的特征矩阵。卷积函数见式（8）。

下采样层：下采样也称为池化，池化分为平均池化和最大池化。本模型采用的是平均池化，运算结果可由式（10）表示。

经过池化后输出的特征图变为原来的1/n。

实验采用的CNN模型在原有LeNet-5模型的基础之上去掉全连接层，将第二层卷积层的卷积核设置为1，通过连接的softmax 分类器输出不同的故障类型，总体结构为2个卷积层，2个池化层和1个输出层。CNN模型结构见图1。

图1 CNN模型结构

2 故障诊断整体流程

滚动轴承故障诊断的总体流程包括提取原始振动信号组成待处理数据集，通过EMD 分解得到IMF，对IMF 进行FICA 分析并选取前6 个ICA 分量组成样本集，划分训练集与测试集，训练与测试模型，整体流程如图2所示。

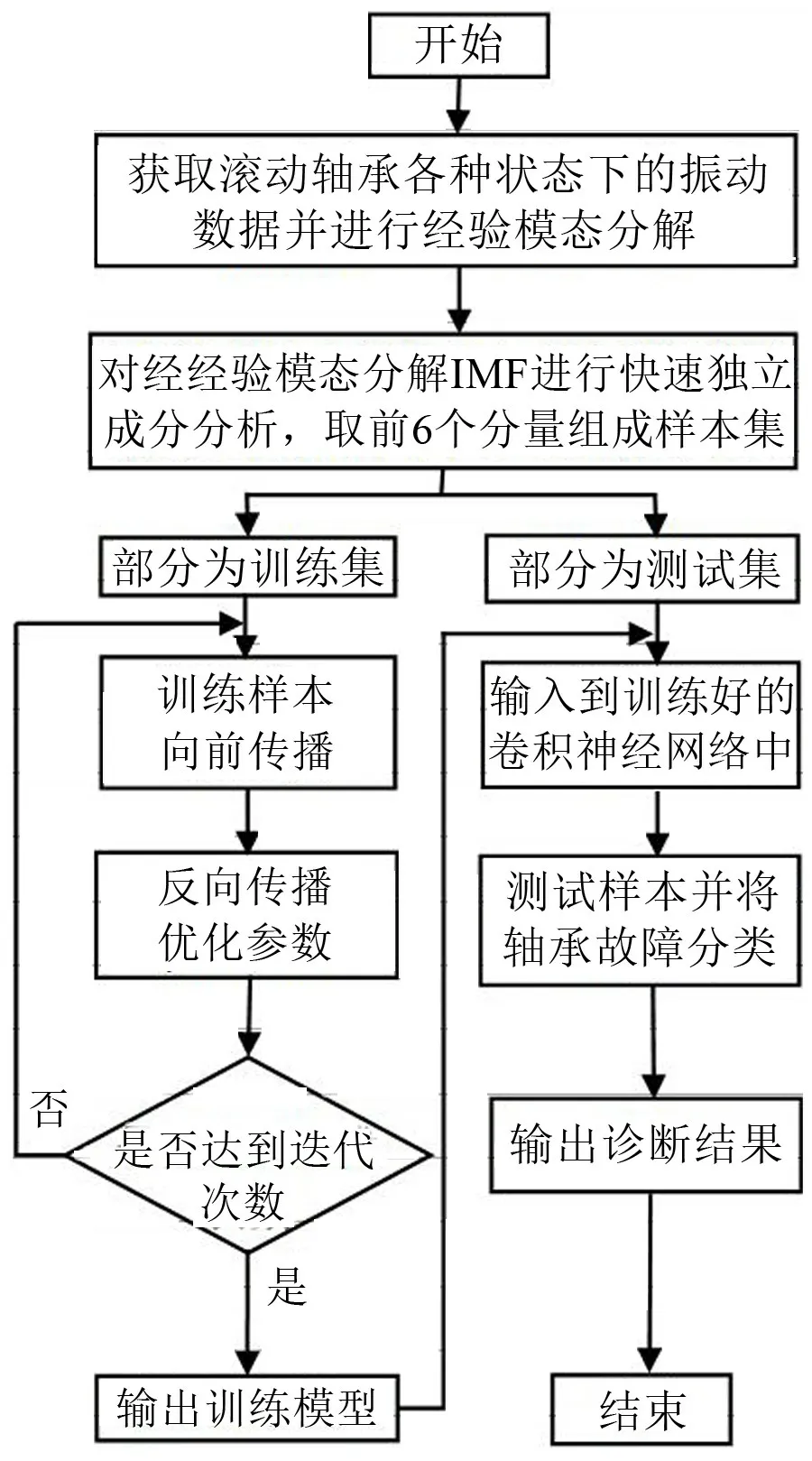
图2 故障诊断流程图

3 数据处理及实验结果分析

3.1 实验数据来源与原始信号预处理

本实验采用美国凯斯西储大学公开的轴承故障数据。采集背景：实验采用加速度传感器采集振动信号，以12 KHz的采样频率采集电机驱动端振动信号。电机转速分别为1 730 r/min、1 750 r/min、1 772 r/min、1 797 r/min。轴承型号是SKF6205-2RS，使用电火花加工技术在轴承上布置了单点故障，故障直径分别为0.007英寸、0.014英寸、0.021英寸，分别布置在滚动轴承内圈、外圈、滚动体。分别选取滚动轴承内圈、外圈、滚动体的各3种故障类型以及正常状态下的数据共10 种数据集组成样本集，选取1 730 r/min 至1 797 r/min 区间内4 种工况数据，每个状态下的样本包括4 种转速下的变工况振动信号数据，每个数据集包含600个样本，每个样本包含400个数据点。赋予其对应的标签，标签形式采取“独热”的编码(one-hot encoding)方式，即若选取的数据为内圈轻度损伤，视其为第二种情况，即第二个位置数字编码为1，其余数字均为0，如“[0，1，0，0，0，0，0，0，0，0]”，其余状况标签以此类推。网络参数设置：每种状态下训练样本与测试样本之比为3:1，学习率为0.5，偏置为0，批次处理样本数为5，C1卷积核大小为11；S1卷积核大小为2；C2卷积核大小为5；S2卷积核大小为1。滚动轴承数据说明见表1，轴承内圈轻度损伤时振动信号经EMD 分解后提取的6 个IMF 分量与EMDFICA后的前6个ICA分量见图3、图4。

表1 轴承故障数据说明

图3 基于EMD所得IMF分量

由图3可以看出，原始振动信号经过EMD分解后故障特征不够明显。而经过EMDFICA 后，得到了组成各IMF 的独立信号源与混合系数矩阵，如图4所示。这使得滚动轴承各种状态下信号特征更加明显，便于CNN 进行特征学习。通过此方法，可以使得神经网络在层数和参数减少的情况下准确对故障信息进行学习与分类，实现高精度故障诊断。

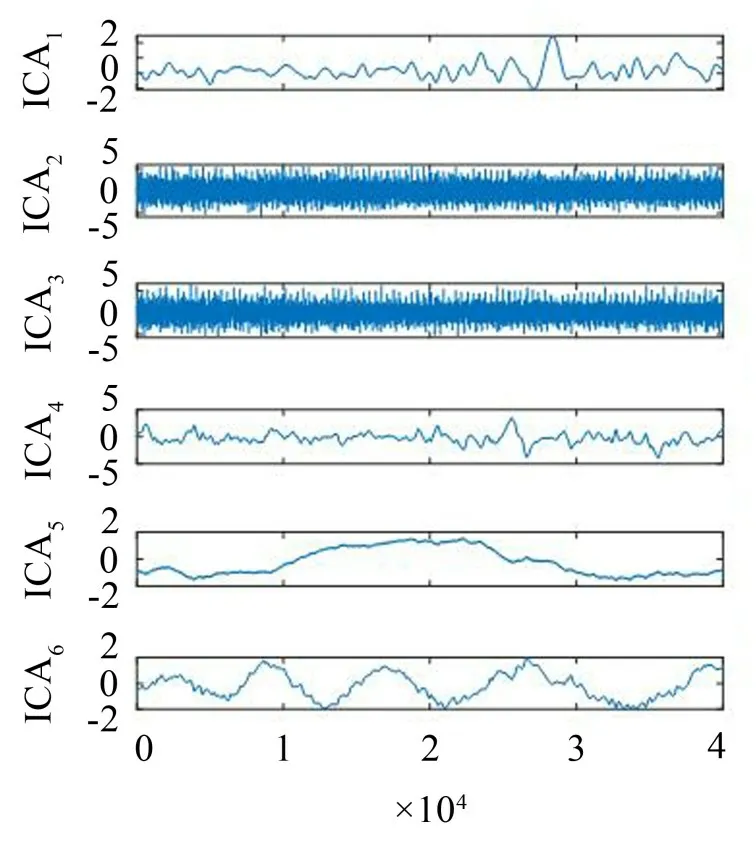
图4 基于EMDFICA所得ICA分量

3.2 实验验证及结果分析

为验证论文采用的EMDFICA 结合优化后的CNN的方法能够快速高效地提取原始信号特征，首先采用“遍历”法列出所有S1卷积核大小为2与S2卷积核大小为1 的网络结构模型，将原始数据经过EMDFICA 处理后的分量输入到表2 中不同结构的CNN模型中，通过不断学习特征，误差反向传播，优化权重，得到最后的诊断结果如表2所示。

通过表2 实验结果可以看出，第五组EMDFIAC-CNN 模型训练精度和测试精度最高，分别为100%和99.73%。为比较预处理效果，将经过EMD 分解后的IMF 分量输入到相同的CNN 模型中，图5 为EMDFICA-CNN 和EMD-CNN 迭代60 次后模型的训练精度、测试精度及损失函数Loss 值的结果对比。根据实验结果可以看出，EMD-CNN 的最高训练精度为99.225%，测试精度为98.935%，取得最高诊断精度时的CNN 模型仍为结构5。结合Loss值变化趋势可以看出，将EMD与FICA相结合，取得了很好的效果，提高模型特征提取效率，有效地提升了收敛速度，诊断精度与EMD-CNN 相比有所提高。

图5 诊断结果对比

表2 EMDFICA-CNN故障诊断结果

为了证明所提出的EMDFICA 方法能够快速有效地获取信号特征，保证CNN准确地对各种故障进行分类，有助于解决浅层神经网络诊断精度不高的问题。将CNN 模型结构中两个池化层卷积核大小都为设置为2，通过比较EMD 与EMDFICA 与CNN结合后的诊断结果，验证所提出的特征提取方法的可行性。模型结构及实验结果如表3所示。CNN模型其余参数设置与之前相同。若可以得出以下结论，即在采用卷积核为2的池化层时EMDFICA仍然能够有效提取信号特征，基于模型仍能取得较好的诊断结果，而结合EMD 分解的CNN 模型诊断结果训练精度和测试精度并不够高，则可以说明采用EMDFICA对信号进行预处理提高了模型的鲁棒性。

表3 EMD-CNN和EMDFICA-CNN诊断结果对比

由表3 可以得出：当第二层池化层卷积核大小为2 时，所采用的EMDFICA-CNN 模型结构依然能够有效提取并保留故障特征，实现高精度诊断，通过与表2 对比可知，优化后的模型训练精度达到100 %，测试精度提高了2.39 %。由于基于传统的EMD 方法所提取的特征不明显，在结合浅层CNN时学习能力变差，导致模型诊断精度低。并且即使调节网络参数，诊断结果也无明显变化，变化幅度仅为10%左右，由此可看出采用的EMDFICA 预处理方法在结合浅层CNN进行故障诊断时的独特优势。

为了验证文中采用的EMDFICA 数据预处理方法结合文中提出的CNN 模型的优势，将特征提取(Feature extraction，FE表示提取每组样本中时域、频域及包络谱特征值)、快速傅里叶变换(Fast Fourier Transform，FFT)、WT 分别与文中提出的CNN 进行结合。为使各模型诊断结果趋于稳定，EMDFICACNN迭代60次，其余3种模型均迭代150次，除此之外，其他模型参数设置均相同。训练精度和测试精度及损失函数如图6所示。

由图6 结果可以看出，文中采用的信号预处理方法结合优化的CNN 模型在有限的诊断次数里能够将诊精度果快速提高并使之趋于稳定，显示出模型有很好的鲁棒性。通过Loss 值可看出，由于其他几种预处理方法提取特征效果差，无法从原始振动信号中准确获得有效故障信息，导致模型收敛速度慢，最终的诊断结果也受到影响。这可与图6 中的训练精度及测试精度的变化趋势相互印证。

图6 不同数据预处理方法诊断结果对比

为了证明经优化后的CNN在结合EMDFICA时的故障诊断结果优于其他模型，将经过EMDFICA处理后的数据输入到BPNN、浅层神经网络(Shallow neural network，SNN)、堆叠自动编码器(Stacked auto - encoder，SAE)、多层感知机(Multi - layer perceptron，MLP)以及二维普通卷积神经网络（2Dimension CNN，2DCNN）中。调节各参数，各网络模型分别迭代60次，实验中样本预处理及训练测试比例完全相同。为排除实验偶然性，对于各模型均进行10次计算后将结果取平均值，如表4所示。

由表4 所示实验结果可以看出，将原始振动信号经EMDFICA 预处理后，在结合上述各模型时均取得了较好的诊断结果，其中结合文中提出的优化后的CNN模型各类故障分类效果最好，诊断精度最高，说明在此条件下EMDFICA-CNN 为理想的诊断模型。