基于Morris灵敏度分析的弹性-黏弹性层合板阻尼性能代理模型构建
2021-08-21吴云鹏
吴云鹏,郑 辉
(上海交通大学振动、冲击、噪声研究所,上海200240)
黏弹性材料由于同时表现出类似固体和液体的性能,具有优良的阻尼性能,被广泛应用于汽车、航空、航天等行业装备的减振降噪设计[1]。但是黏弹性材料的力学性能尤其是刚度性能较差,因此实际工程应用中通常会使用夹层结构,即在刚度较大的各向同性金属层或各向异性复合材料层间嵌入黏弹性阻尼层,以强化结构的力学性能。Kerwin 等[2]针对各向同性黏弹性材料夹层结构建立了力学和声学解析模型。为了进一步改善弹性-黏弹性层合结构的力学或声学性能,还需要进一步对阻尼层的内部结构进行设计,而本文中则通过对黏弹性层开孔并填充高强度材料的方式提高其力学性能,这种阻尼层内部结构的复杂性以及各项异性材料的存在,一方面使得弹性-黏弹性层合板的分析和优化设计仍然以有限元分析为主[3–9],另一方面也使得这类结构的优化设计所涉及的参数数量进一步增加。
对于弹性-黏弹性夹层结构的力学和声学性能优化,学者们已开展诸多研究。Teng 和Hu[3]通过研究黏弹性夹层梁阻尼性能发现,阻尼层厚度对结构整体的阻尼性能影响较大。而Arvin 等[4]针对各向异性黏弹性梁分析了其阻尼性能随阻尼层厚度的变化规律。也有不少学者从参数灵敏度的角度出发研究黏弹性层合板的关键影响参数,并对计算和优化方法进行改进。Akoussan 等[5]结合灵敏度分析和基于梯度的优化方法进行了黏弹性层合结构的局部优化设计,并通过算法优化降低了运算量。但是这些工作大多围绕局部优化展开的。而通过全局优化对黏弹性阻尼材料进行优化设计的难点在于,全局优化算法运算量远高于局部优化算法,并且运算量显著受到待优化问题维数的影响,随着输入变量数目的增加会迅速增长。为了克服全局优化算法运算量过大的问题,一方面有学者针对全局优化算法进行改进,如杨洋等[6]通过对遗传算法进行优化有效降低了收敛所需的代数。另一方面,关于使用代理模型对黏弹性材料的相关性能进行拟合与预测的研究也在不断深入。臧献国[7]使用响应面代理模型结合模态响应法对轿车车身结构进行了优化设计。而魏星等[8]则发现通过使用代理性较好的代理模型,可以使得有限元模型的调用次数降低至直接优化的1/4 至1/6。但这些使用代理模型进行全局优化设计的研究并非通过参数灵敏度分析筛选高灵敏度参数构建代理模型,对于复杂结构构建的代理模型维数依然很大。
参数灵敏度分析对代理模型的优化主要体现在两方面,首先是通过降低问题维数,可有效减少后续全局优化的运算量并提高收敛性;其次在稳健性分析中能够评估结果的鲁棒性。本文主要关注灵敏度分析的第一类作用,即降低问题维数的作用。
目前动力学和声学灵敏度分析常用的方法为伴随变量法,其本质是基于偏导数计算的摄动分析法,该类方法的优势是运算量较小,缺点是仅能反映某个参数在局部范围内的灵敏度。而Morris方法能够反映某个参数在全局范围内的灵敏度,缺点为运算量高于摄动法。
本文在嵌入开孔阻尼层的弹性-黏弹性层合板阻尼性能代理模型构建中,通过灵敏度分析对模型进行降维简化。首先分别使用摄动法和Morris方法对层合板的1 阶模态阻尼比进行参数灵敏度分析,根据分析结果筛除相对不敏感参数,之后使用多项式响应面法对模型1 阶模态阻尼比进行拟合,并用构建的代理模型预测新采样点的1阶模态阻尼比并计算其均方根误差,评价代理模型的代理性能,通过对比明确两种灵敏度分析方法对构建代理模型的简化效果。
1 参数灵敏度分析
1.1 摄动法
摄动法的基础是在感兴趣的点(通常情况下是参数变化范围的均值点,或是初始模型的参数值)周围使用泰勒展开代替原函数关系,只需要做出1 阶泰勒展开,就可以分析各个模型的均值与方差。模型的响应值f(x) 在x0处的1阶泰勒展开形式如下:

式中:x0i为展开点x0在第i个变量处的分量。利用泰勒展开式,可以对原函数的均值和方差进行估计,当展开点x0恰是输入分布的均值时,有:

如果设计参数之间彼此独立,则C转化为对角矩阵,对角线上的元素为对应设计参数输入量的方差,此时响应量的方差可以表示为各分量方差σi的线性组合:

因此可以通过响应量在展开点附近的偏导数和设计参数的方差描述某个设计参数对响应值的重要性。
在基于梯度运算的局部优化算法中,这一类灵敏度分析方法被广泛使用[4],原因是基于摄动法的灵敏度分析本身能够提供局部优化算法所需的梯度信息,同时在基于梯度的优化算法中,随着优化过程进行,摄动点会发生改变,克服了摄动法只能反映局部灵敏度的劣势。但在使用遗传算法等优化算法的全局优化设计中,梯度信息变得不再必要,并且摄动法给出的灵敏度信息较为粗略。
1.2 Morris方法
由于不同输入变量的取值范围有较大差异,为便于描述,在本文中将采样空间所有维度取值范围放缩至[0,1]之间。基于轨迹的采样策略的Morris方法所需的采样次数为(M+1)×r次[10],其中M为灵敏度分析问题的维数,r描述采样过程中对每个维度的细分程度,采样轨迹可以用维数为(M+1)×r的矩阵B′表示,该矩阵在每列中都包含一个从随机点x∗开始的点。下一个轨迹点通过将x∗某个维度的坐标增加Δ获得,其中:

式中:n为取值范围从1到r-1的整数。
一个满足上述条件的矩阵B′可通过式(5)计算:

式中:J为只包含元素1的矩阵,B为包含一个严格下三角矩阵,而其余部分为零的(M+1)×r阶矩阵。起始点x∗的必要条件为从该点沿任意维度增加Δ后仍在可行域G内。
通过上述方法获得的采样点除起点外轨迹都是固定的,为了克服这一问题,Morris 提出了式(6)所示的更有随机性的采样方式[10]:
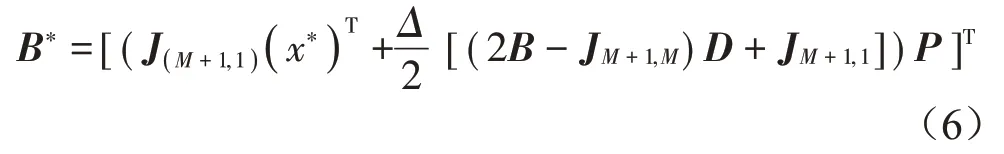
式中:矩阵D为M×M阶对角矩阵,其对角线元素以相同的概率随机取1或-1,矩阵P为M×M阶单位矩阵的随机置换矩阵。 给定一个输入x={x1,x2,…,xN}∈G,并要求满足xi+Δ<1,则xi对于函数值变化的贡献可以通过式(7)描述。

在G内随机获取多组采样点,并对每个点都计算di(x),通过计算该组数据的平均值和标准差,可以分别从不同的角度评估某个输入变量的重要性:平均值主要描述输入变量xi自身的重要性;而标准差从另一方面描述变量的重要性,如果变量xi的评估指标di(x) 有着较高的标准差,则变量xi的重要性主要来自该变量的非线性行为或与其他输入变量的相互作用。
由于存在非线性关系,一些变量的效果可能会在不同取值范围内相互抵消,为了避免这种情况出现,Campolongo 等[11]在2007年引入了新评估方法,即使用函数di(x)绝对值|di(x)|的算术平均*作为新评估标准。新评估方法避免了某个参数在不同取值范围内由于效果符号改变造成互相抵消,但也忽略了有关输入变量重要性的符号信息,需与先前的和组合使用,在不进行额外采样的情况下可以分析每个输入变量的实际重要性和这种贡献性质(线性、非线性或相互作用)的更完整信息。
相比于摄动法,Morris 方法的显著优势在于能够识别响应值与某个输入变量之间的非线性关系,并提供某个参数在一定取值范围内的整体贡献。因此Morris方法对于存在非线性行为函数的灵敏度分析结果比摄动法更精准,如果在摄动点附近某个参数对目标函数的影响要大于或小于在其他区域内的影响,则摄动法可能会高估或低估该参数的重要性,Morris方法则能综合评价某个指标在取值范围内的重要性。此外如果模型存在明显的非线性行为,或是某个参数和目标函数的相关性以线性关系为主,都可以通过Morris 分析进行区分,因此除了针对代理模型的元素数量进行简化,通过Morris 灵敏度分析还可以针对代理模型中包含某个元素的线性项或非线性项进行简化,这对于代理模型的建模和简化过程更有指导作用。
1.3 参数灵敏度分析结果及讨论
用有限元商业软件COMSOL 计算参数灵敏度分析所需模型1阶阻尼比。用于结果比较的模型为图1 所示的阻尼层开孔的弹性-黏弹性层合板,层合板外形尺寸为200 mm×200 mm×1.2 mm,层合板的边界条件为四边固支。

图1 阻尼层开孔的层合板示意图
阻尼层料使用黏弹性材料SA-3C[9],其杨氏模量和阻尼损耗因子具有频变特性,函数关系为

式中:E(f)为阻尼材料的杨氏模量,单位为MPa,f为频率,单位Hz,β(f) 为材料的黏弹性损耗因子。由于弹性-黏弹性阻尼层合板的黏弹性阻尼材料层的杨氏模量和阻尼损耗因子具有频变特性,需通过迭代方法[9]获得夹层板1 阶模态的特征频率与阻尼损耗因子,迭代方式如图2 所示。计算时设定特征频率的最大容差为0.02 Hz。

图2 阻尼比迭代计算流程
得到模型的1阶模态特征频率后,按式(9)计算模型1 阶模态阻尼比,并将其作为弹性-黏弹性阻尼夹层板阻尼性能的评价指标。

式中:ζ1为模型的1 阶模态阻尼比,Im(f1)为1 阶特征频率的虚部,|f1|为1阶特征频率的模。
将弹性-黏弹性层合板可在一定范围内变化的参数作为输入变量,分别用摄动法和Morris 方法对这些变量进行参数灵敏度分析,采用摄动法计算时的采样数量为8 组,采用Morris 方法时的采样数量为24组。
实际层合板的参数变化来自两方面,首先是通过尺寸设计人为控制的尺寸参数,其次为加工精度导致的材料性能差异。可以人为控制的尺寸参数包括阻尼层厚度、阻尼层中面至层合板中面的偏移量、阻尼层开孔边长和相邻孔间距,其中,阻尼层厚度x1变化范围为0.2 mm~0.24 mm,阻尼层中面到层合板中面的偏移量x2变化范围为-0.2 mm~0.2 mm。阻尼层开孔边长d变化范围为20 mm~90 mm,相邻两孔的间距l变化范围为88 mm~90 mm。
金属层和开孔处的填充物为铝合金,其杨氏模量E1在67.9 GPa~69.9 GPa 的范围内浮动,密度ρ1为2 740 kg/m3,泊松比v1为0.3。并且认为阻尼层材料的密度ρ2变化范围为1 425 kg/m3~1 475 kg/m3,泊松比v2变化范围为0.46~0.52。
首先设定所有可变参数的取值均为取值范围的中值,代入有限元模型验证迭代程序的可行性,经计算,模型的1阶特征频率为210.67 Hz+16.830 Hz,依据式(8)获得黏弹性材料的杨氏模量和阻尼损耗因子,并将新的材料参数代入有限元模型计算其1 阶模态,计算结果如图3所示。
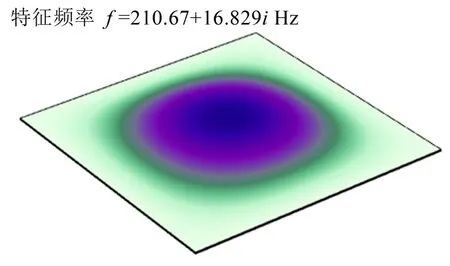
图3 模型的1阶模态有限元计算结果
通过对比可以发现,最后一次迭代前后的1 阶特征频率已经非常接近,能够满足最大容差要求,可以将该结果应用于后续的灵敏度分析。
摄动法的灵敏度分析结果如图4 所示。由图4结果可以发现,高灵敏度参数分别为阻尼层厚度x1、阻尼材料泊松比v2、开孔边长d和开孔间距l。参数x1灵敏度较高的结论符合文献[3]中关于阻尼层厚度能够显著影响阻尼性能的描述,而开孔边长对阻尼性能影响较大的原因在于开孔的大小会直接影响阻尼层的质量占比,从而对阻尼性能产生较大影响,因此也符合对计算结果的预期。
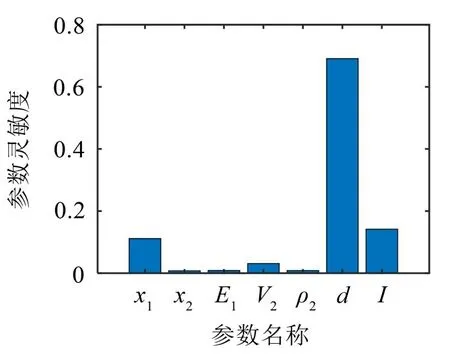
图4 摄动法灵敏度分析结果
Morris 方法灵敏度分析结果如图5 所示。与摄动法分析结果的主要不同在于:基于Morris 方法分析结果表明,阻尼层中面偏移量x2也有较高的灵敏度,而基于摄动法分析结果则表明该参数的灵敏度很低。通过进一步观察基于Morris灵敏度分析结果的纵轴坐标可以发现,参数x2的灵敏度主要来自于自身的非线性行为或与其他参数相互作用,而当使用函数绝对值|di(xi)|作为Morris 灵敏度分析的评估指标时,其参数灵敏度进一步提高,这表明x2可能存在对目标函数值的贡献度相互抵消的情况。

图5 Morris方法灵敏度分析结果
2 代理模型的代理性能比较
2.1 代理模型构建
代理模型的主要工程意义在于,对于需要经过高精度有限元分析或实验才能获得的数据,通过使用结果与有限元分析结果相近而所需运算量却远小于有限元计算的近似模型进行预测,可以在满足一定精度要求的同时显著减少运算量。
本文将要构建的代理模型为多项式响应面代理模型,是工程上较为常用的一种代理模型方法,其一般形式为

式中:y为采样点获取的数据,β0、βi、βii、βij为待定系数,xi、xj为输入变量,ε为近似误差。
通过最小二乘法可获得待定系数表达式:

式中:β为待定系数矢量,X为设计变量矩阵。
首先根据本项目中的输入变量的取值范围进行采样,获得采样点中输入变量的取值后生成设计变量矩阵,并将采样点处获得的有限元分析结果记录为矢量y,之后根据式(11)获得待定系数矢量β,将结果代入式(10)即可获得代理模型表达式。
2.2 代理模型的性能比较
为了评估基于Morris灵敏度分析和基于摄动法的灵敏度分析建立的代理模型的代理性能,分别使用根据Morris分析方法获得的高灵敏度参数(x1、v2、d和l)和根据摄动法获得的高灵敏度参数(x1、x2、v2、d和l)对层合板的一阶模态阻尼比进行二项式响应面建模,建模点数量均为40 组。获得代理模型后,分别使用两组代理模型预测20组新采样点的1阶模态阻尼比,将预测结果与有限元计算结果进行对比,并计算预测结果的均方根误差,即:

其中:nt为预测采样点的数目,此处取20。yi为待预测点的真实函数值,通过有限元计算获得。为待预测点的预测值,通过代理模型计算获得。
将分别用摄动法和Morris方法进行灵敏度分析构建的代理模型的代理性能与不进行灵敏度分析、直接用全部参数进行代理模型建模的情况进行对比,结果如表1所示。

表1 代理模型的代理性能对比
结果表明,虽然通过摄动法筛选获得的高灵敏度参数数量更少,模型的形式也更为简单,但是模型的均方根误差显著高于另外两种情况,这表示模型的代理性严重不足。而通过Morris方法构建的代理模型却能保持良好的代理性能,其均方根误差低于无灵敏度分析直接建立代理模型的情况。考虑到基于摄动法和Morris方法灵敏度分析的主要区别在于两者对于参数x2的重要性判断不同,为了确认参数x2的重要性,现将所有输入变量的数值设定为各自取值范围的中值,随后使x2在取值范围内由低到高逐步变化,并计算模型1 阶模态阻尼比。之后针对摄动法分析结果中有较高灵敏度的参数d进行同样的操作,将两者对阻尼比变化的影响程度进行对比,计算结果如图6所示。

图6 不同参数对模型阻尼比的影响
不难发现,通过调节阻尼层中面的偏移量,层合板的1 阶模态阻尼比变化范围为0.061 1 至0.079 6,变化幅度超过30%,而且阻尼比与x2的关系曲线为单峰曲线,符合x2存在对目标函数值的贡献度相互抵消情形的预判。而通过调节阻尼层开孔的边长实现的阻尼比变化范围为0.077 4至0.081 3,变化幅度约为5%。这表明阻尼层中面的偏移量x2对层合板1阶模态阻尼比的影响程度要远高于阻尼层开孔边长d。摄动法对于参数x2的灵敏度给出了错误的判断,主要原因为:在摄动点附近,随着参数x2的改变,模型1 阶模态阻尼比的变化较为平缓,摄动法将摄动点处阻尼比的变化情况作为对整体范围内变化情况的预估,低估了x2的重要性。而Morris 方法则能够对每个维度取多个点进行全面考察,避免对参数灵敏度做出错误判断。
3 结语
本文将基于Morris 方法与基于传统振-声学优化中常用的摄动法灵敏度分析应用于开孔阻尼层的弹性-黏弹性层合板1 阶模态阻尼比代理模型的构建,以降低模型维数和加速后续将进行的黏弹性阻尼层参数优化进程。以一弹性-黏弹性-弹性阻尼夹层板为例,对分别用这两种灵敏度分析方法辨识高灵敏度参数后构建的阻尼代理模型与不进行灵敏度分析、直接用全部参数构建的代理模型进行了代理性能对比。结果表明:虽然通过摄动法获得的高灵敏度参数数量更少,代理模型的形式也更为简单,但是模型的新采样点预测结果均方根误差显著高于另外两种情况,表明模型的代理性能严重不足;而通过Morris方法构建的代理模型却能保持良好的代理性能,其新采样点预测结果均方根误差甚至低于无灵敏度分析直接建立代理模型的情况。研究结果可为嵌入式阻尼金属或复合材料层合板的高阻尼结构参数优化代理模型构建提供依据。
需要说明的是,虽然Morris 方法相较于摄动法不易对参数的重要性做出误判,但运算量高于摄动法,本文采用Morris 方法进行参数敏感性分析时的采样点数量达到摄动法的3倍。但是在阻尼优化设计等问题中,需要直接使用代理模型代替有限元模型输出结果,如果参数灵敏度分析结果出现错误,将会使得降维简化后的代理模型失去代理性,进而使得整个优化过程的结果失去意义,因此在代理模型构建阶段使用精度更高的灵敏度分析方法仍是有必要的。
