基于多信号流图的测试性建模与分析方法
2021-08-21赵杰唐建立靳为东申双荣季桓勇
赵杰,唐建立,靳为东,申双荣,季桓勇
(中电科思仪科技股份有限公司,山东青岛,266555)
0 引言
随着我国科学技术的飞速发展,大型设备在向精密化、复杂化、大型化、信息化等方向发展的同时,也给使用、维修和保障带来了严重制约,这就需要故障诊断、故障预测与健康管理等技术应用于大型设备的设计过程中,降低维修成本、提高保障效率,其中测试性尤其是测试性模型的构建作为设计的核心和关键环节,起着至关重要的作用。
相比国外,国内对测试性建模的研究起步较晚,目前研究和应用较为广泛的是信息流模型和多信号流图模型,但由于故障和测试的不直接相关性,本文重点考虑以多信号流图模型主,通过功能信号的引入,将故障与测试的关系明确,建立与大型设备功能框图类似的模型结构图,便于知识与经验的表达。
1 多信号流图模型
■1.1 多信号流图简介
多信号流图模型是一种系统可测性分析、PHM系统设计中常用建模方法,与信息流模型的区别在于,多信号流图模型以多个单信息流模型为基础,融合到系统的结构模型中,因此,多信号流模型将反应系统中各模块以及元件间的最真实的连接关系。该测试性分析方法是由Somnath Deb等人于1994年提出的,在模型中主要包括两种故障模式:功能故障和一般故障,其中功能故障是指系统正常运行但功能指标发生偏差,一般故障是指导致系统不能正常运行的故障。
多信号流图建模以故障信号传播为基础,在故障空间进行建模,不需要构建完整的系统模型,利用分层有向图表示系统结构的依赖关系,可应用于复杂系统的测试性设计、故障模式影响与危害度分析、故障诊断与预测、自动测试系统等。
多信号流图将模拟信号的真实流向,构建层次化的多维空间,覆盖多个信息流模型,更加接近于系统的物理结构,但其本质仍然是构建依赖矩阵,再进行测试性分析。
■1.2 多信号流图模型
在多信号流图模型中,以影响结果为划分标准,把故障模式分为两类:一是功能故障,主要指系统中各组成单元的故障,该类故障能够导致系统的部分功能失效,但整个系统不会因此完全崩溃;二是一般故障,主要指系统中个组成单元发生的故障,不仅使得整个系统功能完全失效,甚至会导致整个系统完全崩溃,不能正常工作。因此,根据上述描述,可以将多信号流图模型中的信号划分为两种状态:正常状态、异常状态,其测试结果分别为“通过”或“不通过”。
本文中的多信号流模型主要包含七类:有限模块集合、模块中的信号特征集合、有限测点集合、测点中的有限测试集合、每个故障对应的信号特征集合、每个测点对应的测试集合、每个测试可检测的信号特征集合等。其中,模块中信号数量是一个有限值,信号之间的联系是相互独立的,并可以明确区分各个信号。因此,在测试性模型中各信号都是相对独立,不会对其他信号产生影响。多信号流图模型的优点是模型构建简单、易于理解、更加真实。
多信号流图模型主要由以下元素组成:
(1)有限模块集合: M = {m1, m2,…,mx};
(2)信号特征集合:S ={s1,s2,…,sy};
(3)有限测点集合: Tp = {T p1, Tp2,…,Tpz};
(4)有限测试集合: T ={ t1,t2,…,tu};
(5)每个故障对应的信号特征集SM(si);
(6)每个测点对应的测试集SP(tpi);
(7)每个测试可检测的信号特征集ST(ti);
系统的多信号流图模型 DG ={M ,Tp,E},其中E为有向无环图的边,表征信号流向,代表系统的物理连接。
本文中的“多信号”专指受独立元件所影响的相互独立的有限的信号集合,即一个信号只包含一个故障信息,各信号间是相互独立的,同时也是互不影响的。实际上,多信号流图模型是以系统结构模型为基础,融入依赖模型,因此需要明确各信号之间的依赖关系,确定其对系统故障诊断是必要且有效的,同时还需明确依赖关系与实际系统之间映射关系,使建模直观简单。
2 测试性分析
■2.1 依赖矩阵生成
大型复杂系统中节点数目众多,故障与测试之间的相关关系较为复杂,通过模块定位层级来确定矩阵故障信息的层级,考虑存在多层子级模型的情况,遍历模型图求取故障与测点的邻接矩阵,然后通过可达矩阵算法–Warshall算法求取可达矩阵,进而求解一般故障依赖矩阵,然后以一般故障依赖矩阵为基础,通过分析故障模式与测试之间的信号关联关系确定功能故障依赖矩阵,最后将两种故障测试以来矩阵进行组合,即获得分析对象的故障–测试以来矩阵。
(1)邻接矩阵
邻接矩阵()A G是表示有向无环图中各顶点之间相邻关系的矩阵,有向无环图 ( )G=V,E,有两种不同的表示方式:邻接表与邻接矩阵。其中,邻接表表示稀疏图比较紧凑,但在依赖矩阵生成过程中邻接表并不适用,因此本文采用了邻接矩阵作为有向图的表示方法,满足后续矩阵计算。邻接矩阵是整个依赖矩阵生成的第一步,为可达矩阵与依赖矩阵提供计算基础。
(2)可达矩阵
可达矩阵()P G以邻接矩阵为基础,通过可达矩阵算法,生成测试性模型的可达矩阵。可达矩阵的定义:假设有一个有向图 G=( V,E),将途中的每个顶点按照顺序进行编号:1,2,…,Vcount,则有向图G的可达矩阵表示为的矩阵其中:

由上述计算公示可知,通过可达矩阵,可计算出任意两个节点间是否存在一条通路,或者任一节点自身是否存在回路。根据依赖矩阵的定义,只需明确任意两节点之间是否存在通路,因此可达矩阵采用0–1二值矩阵的方式进行表示。考虑到实际模型的复杂性,本文选取了复杂度较低的可达矩阵算法–Warshall算法。
(3)故障测试依赖矩阵
通过上述求出的可达性矩阵P (G)是一个n×n的矩阵,表示有向图G中各个顶点之间是否具有相互连通关系。映射到多信号流图模型,可达矩阵表示各个模块与测点之间是否具有互连通关系。将可达矩阵中代表模块的行和代表测试的列提取出来,就可获得有向图G的一般故障依赖矩阵,其提取流程如下:
第一步:筛选可达矩阵的行与列
在可达矩阵中,行或列所代表的节点信息涵盖了模块节点、测试节点等,而依赖矩阵中行代表模块节点信息,列代表测试信息。因此,为方便展示以及测点中测试的展开,对可达矩阵中不需要的行列进行删除,保留表示模块的行、表示测点的列。
第二步:展开测点中的测试
筛选完成后的可达矩阵中列代表的是一个测点,而依赖矩阵要求每列代表一个测试,因此,需要依据测点中测试的个数,对依赖矩阵中的列进行拓展。由于获得的是一般故障依赖矩阵,无需考虑模块中信号与测试中信号的关联问题,因此同一测点中的测试信息是完全相同的。
■2.2 典型测试性指标
测试性指标是对大型设备可测试特性的描述,在构建完模型之后,通过计算生成故障测试依赖矩阵,将其作为数据输入,生成测试性分析报告,便于设计人员查看。本文重点介绍故障检测率和故障隔离率:
(1)故障检测率(FDR)
故障检测率是指在规定时间内,被测系统的故障能够由测试设备检测到的故障数与所有可能的故障总数的百分比。其数学模型为:
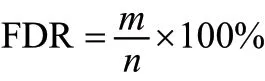
式中m:故障–测试依赖矩阵的非零行数;n:故障–测试依赖矩阵的总行数。
(2)故障隔离率(FIR)
故障隔离率是指在规定时间内,被测系统检测到的故障能够由测试设备正确地隔离到规定等级和个数的故障数与检测到的故障总数的百分比。其数学模型为:
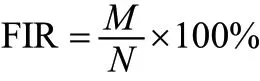
式中M:故障–测试依赖矩阵中,所有无重复行的行数;N:故障–测试依赖矩阵的总行数。
3 典型应用
对于系统级测试性建模功能的典型验证,本文以某雷达发射机系统为例进行建模验证,根据其功能划分为如图1所示的12个LRU级模块以及13个测点,采用本单位自研的测试性建模与分析软件进行测试性模型的构建,其测试性模型如图1所示。
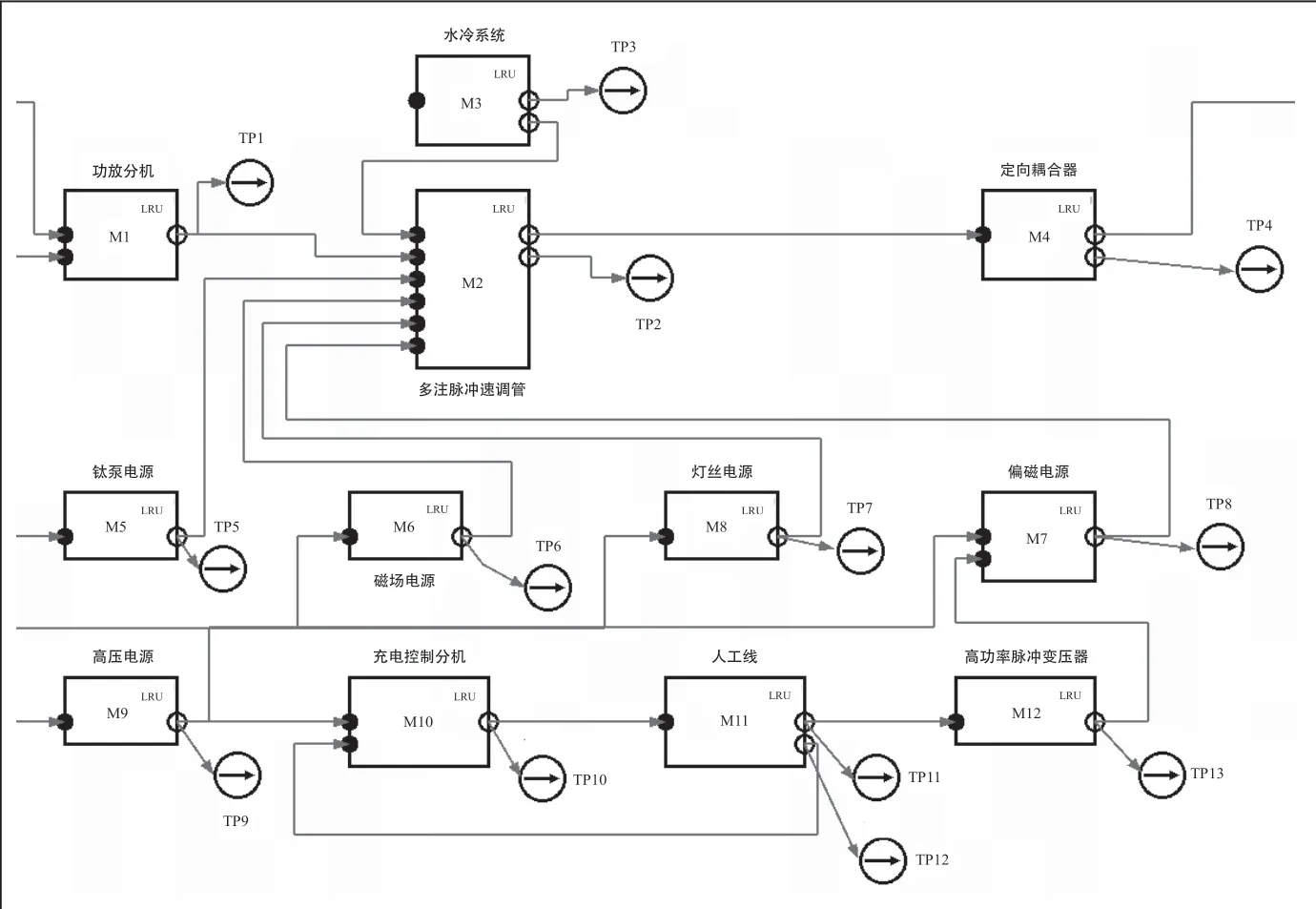
图1 某雷达发射机系统的测试性模型
其中有限模块集合为{M1功放分机、M2多注脉冲诉调管、M3水冷系统、M4定向耦合器、M5钛泵电源、M6磁场电源、M7偏磁电源、M8灯丝电源、M9高压电源、M10充电控制分机、M11人工线、M12高功率脉冲变压器};
各模块对应的信号特征为:M1{功放输出功率信号、放大器功率增益},M2{速调管幅频特性、速调管输入输出特性、速调管收集极电流、速调管管体电流},M3{收集极水流量、收集极水温、环流器水流量、管体水流量},M4{射频包络、发射极输出功率},M5{钛泵电压、钛泵电流},M6{磁场电流},M7{偏磁电流},M8{灯丝电流},M9{高压电源电压、高压电源纹波系数},M10{赋能电流、调制器充电电流、IGBT驱动信号},M11{调制器反峰电流、人工线电压、脉冲功率},M12{调制波信号}。
各测点对应的测试为:TP1{固态功放增益测试、固态功放输出功率测试},TP2{速调管幅频特性测试、速调管输入输出特性观测、速调管收集极电流测试、速调管管体电流测试},TP3{流量水温测试},TP4{射频包络测试、功率信号测试},TP5{钛泵电流测试、钛泵电压测试},TP6{聚焦线圈电流测试},TP7{灯丝电流测试},TP8{偏磁电流测试},TP9{高压电源电压测试、高压电源纹波测试},TP10{赋能电流测试、充电电流测试、驱动电压信号测试},TP11{反峰电流测试},TP12{脉冲功率测试},TP13{调制波信号测试}。
应用可视化测试性建模与分析软件建模流程如下:
(1)启动软件,新建文件并保存为某雷达发射机系统测试性模型文件;
(2)根据雷达发射机系统的功能架构以及上述模块和对应信号的关系,从模型视图中拖拽出相应的模块模型或测点模型;
(3)双击模块模型,在新出现的文件中添加相应的故障模式级信号;
(4)在测点属性中添加测试信息,并与信号的功能进行映射,确定其功能依赖关系;
(5)在菜单栏中点击依赖矩阵生成–>测试性分析,可以获取如表1、表2所示的测试性分析报告。
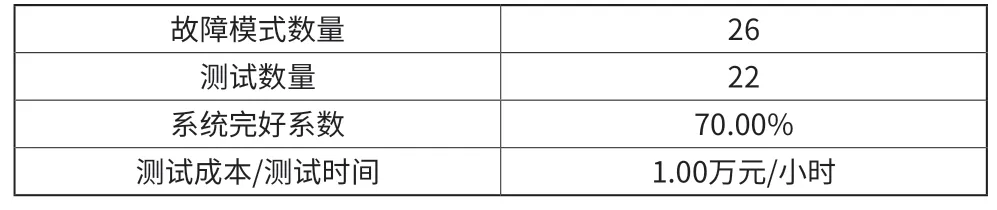
表1 系统模型统计结果

表2 测试指标分析结果
如表1、表2所示,雷达发射机系统模型中包含26个故障模式(即信号特征)和22个测试,经过计算该模型的故障检测率为100%,故障隔离率为76.92%,模糊度为2的模糊组1个,模糊度为4的模糊组1个。
4 结束语
利用层次化建模方法,对大型复杂大型设备系统建立起测试性模型,能够在设计之初快速准确地提供各种测试性相关数据,满足测试性设计的需要。
