基于轻量化与强度的短纤维复合材料蜂窝三明治板结构多目标优化设计

岳科宇 陆正刚 王小超

摘要：蜂窝三明治板在结构轻量化中得到了广泛应用，采用具有良好材料性能的短纤维复合材料替换铝蜂窝，能进一步满足轻量化需求。为了短纤维复合材料更好地应用，针对增大蜂窝三明治板抗拉强度要求，提出了一种增大面板与蜂窝粘接面积的结构设计方案。在有限元软件 ABAQUS中建立了考虑损伤退化的短纤维复合材料蜂窝三明治板有限元计算模型，验证了设计方案的可行性。为了兼顾力学性能和减重要求，采用基于代理模型和多岛遗传算法的优化方法对蜂窝结构参数进行了多目标优化。分析结果表明，所建立的精细化有限元模型能够模拟三明治板的性能突降行为，基于代理模型高效准确的优化流程，优化后三明治板的面密度相比于优化前降低了30%，强度满足要求。

关键词：多目标优化;短纤维复合材料;三明治板;蜂窝结构设计;有限元

中图分类号：TB383             文献标志码：A        文章编号：1009-9492（2021）12-0090-07

Multi-objective Optimization of Short Fiber Reinforced Composite HoneycombSandwich Panel Structure Based on Lightweight and Strength

Yue Keyu ，Lu Zhenggang ※，Wang Xiaochao

（Institute of Rail Transit， Tongji University， Shanghai 200092， China）

Abstract： Honeycomb sandwich panels is widely used in lightweight structure. In order to make further improvement on lightweight， shortfiber reinforced  composite  material  which  has  good  material  properties  can  be  used  to  manufacture  honeycomb  instead  of aluminum. For well-applied of short fiber reinforced composite， a new structure was designed for increasing the bonding area between skin and honeycomb to enhance the flatwise tensile strength. The finite element model of short fiber reinforced composite honeycomb sandwich panel with damage degradation was established based on ABAQUS， by that the feasibility of the new design was proved. Considering the requirements of strength and weight reduction， the multi-objective optimization of honeycomb structure parameters was carried out by using the optimization method based on surrogate model and multi island genetic algorithm. The results show that the finite element model can simulate the failure behavior of sandwich panel well. And the optimization based on surrogate model is efficient and accurate. The density of optimal sandwich panel with acceptable strength is 30% lower than the original design.

Key words： multi-objective optimization; short fiber reinforced composite material; sandwich panel; honeycomb design; finite element

0 引言

蜂窝三明治板具有质量轻、比模量大、隔音、隔热、吸能强、成本低等优点，在航空航天、汽车、轨道交通车辆、海洋船舶、土木建筑等领域已经有了较为广泛地应用[1-4]。为了进一步追求轻量化，轻质高强的纤维增强复合材料也成为了蜂窝三明治板的主要材料。尤其是采用纤维增强复合材料面板和铝蜂窝的三明治板性能已经有了一定的应用和研究[5-8]。

短纤维复合材料由树脂和短切碳纤维组成，强度刚度特性较好，相比长纤维材料，具有更好的工艺性和经济性[9-10]，采用短纤维符合材料替代铝蜂窝结构有望能进一步实现轻量化。而短纤维复合材料目前主要用于一些辅助部件[11-13]，鲜少用于蜂窝制造。采用脆性材料替代铝材制造蜂窝，会使三明治板性能发生改变[14]，但一定程度上仍可以参考铝蜂窝的相关设计经验。对于蜂窝三明治板设计而言，如何权衡轻量化与力学性能之间的关系是值得重点关注的问题。多目标优化是解决此类问题的常用方法，在蜂窝三明治板结构设计中应用较为广泛。XU 等[15]针对夹芯板质量最小化和隔声性能最大化两个目标对三明治板的结构参数进行了优化;Garrido M 等[16]采用直接多搜索方法对复合材料夹芯板系统进行了优化研究，包括了结构的振动、隔热、声学性能、成本等方面;Li 等[17]对扭转和弯曲复合载荷作用下三明治結构以最小重量为目标进行了优化。因此采用多目标优化的方法寻找最优的结构尺寸可以使各项性能达到平衡。但目前国内外在短纤维复合材料蜂窝芯子方面的优化设计研究较少。本文以短纤维复合材料蜂窝三明治板为研究对象，针对粘接后平拉强度较低的问题，提出了一种增大粘接面积的蜂窝设计方案。在此基础上提出了一种考虑多强度的综合轻量化设计方法，通过多目标优化方法，得到了保证力学性能下，以轻量化为目标的蜂窝三明治板结构尺寸最佳组合。

1 短纤维复合材料蜂窝三明治板结构

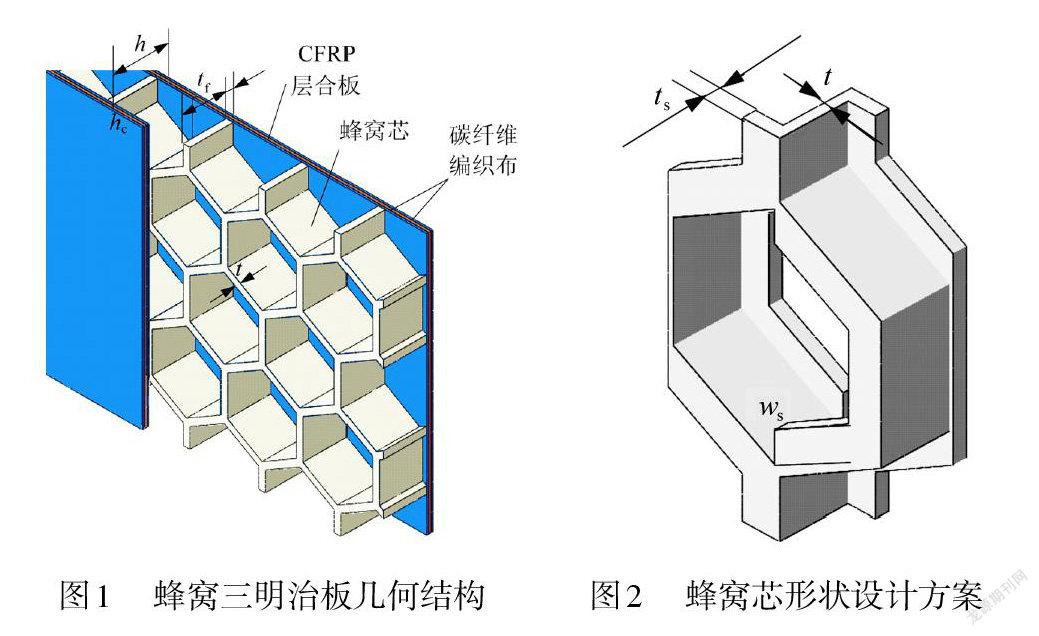
本文所研究的短纤维复合材料蜂窝三明治板由面板和蜂窝芯组成。面板为碳纤维编织布-碳纤维增强复合材料（Carbon Fiber Reinforced Polymer ，CFRP）层合板-碳纤维编织布的形式，蜂窝芯由短纤维复合材料注塑成型，蜂窝单元为正六边形，面板与蜂窝芯之间采用黏合剂粘接。图1所示为短纤维复合材料蜂窝三明治板几何结构，h 为三明治板总厚度，tf 为面板厚度，hc 为蜂窝芯高度，t 为蜂窝壁厚，l 为蜂窝单元边长。

在工程实践中，面板与蜂窝芯之间需要使用粘接剂进行胶结从而形成三明治结构。由于材料的不同和界面属性的差异，短纤维复合材料与粘接剂的结合能力相比于面板与粘接剂的结合能力也会有所不同，这导致了整体的粘接强度将取决于结合能力较弱的一方，也就意味着很难达到理想的粘接强度。而粘接强度对于三明治板的力学强度尤其是平拉强度较为关键，除了表面改性等提高粘接剂与基材间的结合能力的方法外，由于短纤维复合材料注塑成型的优越性，增大粘接面积也是提高平拉强度的有效途径。因此在六边形蜂窝的基础上，设计了如图2所示的新结构，旨在不过多增加蜂窝质量的情况下提高粘接面积而达到增大的目的。该结构通过在六边形蜂窝的上下面增加了半“裙边”形状的加强板，使得粘接面向六边形内扩展，从而增大粘接面积。其中 ts 为加强板厚度，ws 为加强板宽。

2 基于有限元方法的三明治板力学性能计算

2.1 材料本构模型

短纤维复合材料三明治板中的材料均为脆性材料，其在破坏时的性能突降会十分明显。为了能较为准确地模拟出突降行为，需要在有限元建模时考虑材料的损伤退化。针对于短纤维复合材料可能出现的破坏情况，采取了下列损伤本构模型来进行计算。

纤维增强复合材料往往表现出弹性-脆性的行为，其损伤可以通过刚度折减来表征。Hashin准则确定了纤维增强复合材料的损伤初始化，其考虑了4种不同的损伤初始化机理，即纤维拉伸失效、纤维压缩失效、基体拉伸失效和基体压缩失效[18]。具体形式如下：

式中：X T 为纵向抗拉强度;X C 为纵向抗压强度;YT 为横向抗拉强度; YC 为横向抗压强度;S L 为纵向抗剪强度;S T 为横向抗剪强度; α为确定切应力对纤维拉伸初始化准则贡献的系数; σ? 11、  σ? 22、 12分别为有效应力张力的分量，用以评估初始化准则。

当损伤出现之后，对于纤维增强材料，以刚度折减的方法来描述其性能的下降，其应力响应为：

式中：ε为应变;C d 为折减刚度矩阵，其表达式为

其中， Dc =1 - （1 -df ）（1 -dm ）ν12 ν21 ，而df、dm和ds为内部损伤变量，分别为纤维、基体和剪切损伤，由失效模式和损伤演化模型决定。

为了描述短纤维材料的失效，本计算采用了韧性准则。韧性准则是用来预测由于成核、生长和空隙聚集而产生的损伤起始的唯相学模型。图3所示为考虑损伤失效时材料的应力-应变曲线。 σy0 和 εˉ pl 0 分别为损伤初始点的屈服应力和等效塑性应变，此时损伤变量Dd=0; εˉ pl f 为材料完全失效时的等效塑性应变，对应损伤变量Dd=1。

一旦材料达到初始化准则，将采用损伤演化规律来描述材料刚度的退化比例。损伤开始后，各时刻材料的应力张量为：

式中：Dd 为损伤变量（ Dd ≤1），由损伤演化规则计算得到;为有效应力张量（或未受损应力张量），即在没有损伤的情况下材料的应力。当 Dd=1时，材料将丧失承载能力。

本文对于粘接使用内聚力双线性模型（牵引分离模型）来描述[19]。内聚力双线性模型如图4所示，横轴表示位移，纵轴表示应力。

该模型假定损伤的初始化和演化遵循线性。因此界面的应力的初始化响应可以表示为：

式中：σ为界面应力向量（σn 、σs 、σt 分别为法向分量和两个方向的切向分量）; 6为位移向量（δn 、δs 、δt 分别为应力分量对应的位移分量）; K 为刚度矩阵，表征粘接的刚度。

采用二次应力准则来评估粘接损伤初始化，即当三向应力与强度限值（σσσmtax ）之比的平方和为1时，损伤开始：

当损伤初始化后，用损伤变量 D 来描述损伤的演化，随着进一步加载，损伤变量单调地从0增加到1，此时各分量的应力会受到损伤的影响而折减。

2.2 三明治板有限元模型

基于2.1节本构模型，在 ABAQUS 软件中建立蜂窝三明治板模型。面板中 CFRP层合板材料为UD 碳纤维，采用连续壳单元;碳纤维织布材料为12K编织布，和短切纤维复合材料蜂窝芯均采用 C3D8R单元。假定碳纤维织布与 CFRP层合板之间不会分层而采用绑定约束;面板和芯子之间采用表面内聚力行为约束，来模拟面板和芯子间的粘接损伤。对平拉和平压强度计算，采用同一正方形试样，如图5所示;计算时约束底部自由度，在上面板施加拉压载荷。对于三点弯曲计算，参考《GB/T 1456夹层结构弯曲性能试验方法》[20]，取三明治板长400 mm ，宽度60 mm ，跨距360 mm ，如图6所示;压头和支座均设置为刚体，其中支座保留绕 y 轴转动自由度，压头保留 z 向自由度，压头及支座与三明治板之间采用“面面”接触。采用 ABAQUS/Explicit显式动力学进行准静态加载计算。表1～2分别给出了本文有限元模型中內聚力模型参数和蜂窝芯子短纤维注塑材料的参数。

2.3 三明治板主要性能指标

面密度即单位面积内三明治板的质量，衡量了三明治板的重量，截取如图7所示的单胞模型，面密度可以采用下式计算：

式中：tf 为面板厚度;ρf 为面板密度;ρc 为芯子材料密度;l 为蜂窝边长; Vc 为单胞内蜂窝芯子的体积，计算如下：

式中：t 为蜂窝壁厚; ts 为加强板厚度;ws 为加强板宽; Vc 为蜂窝高度。

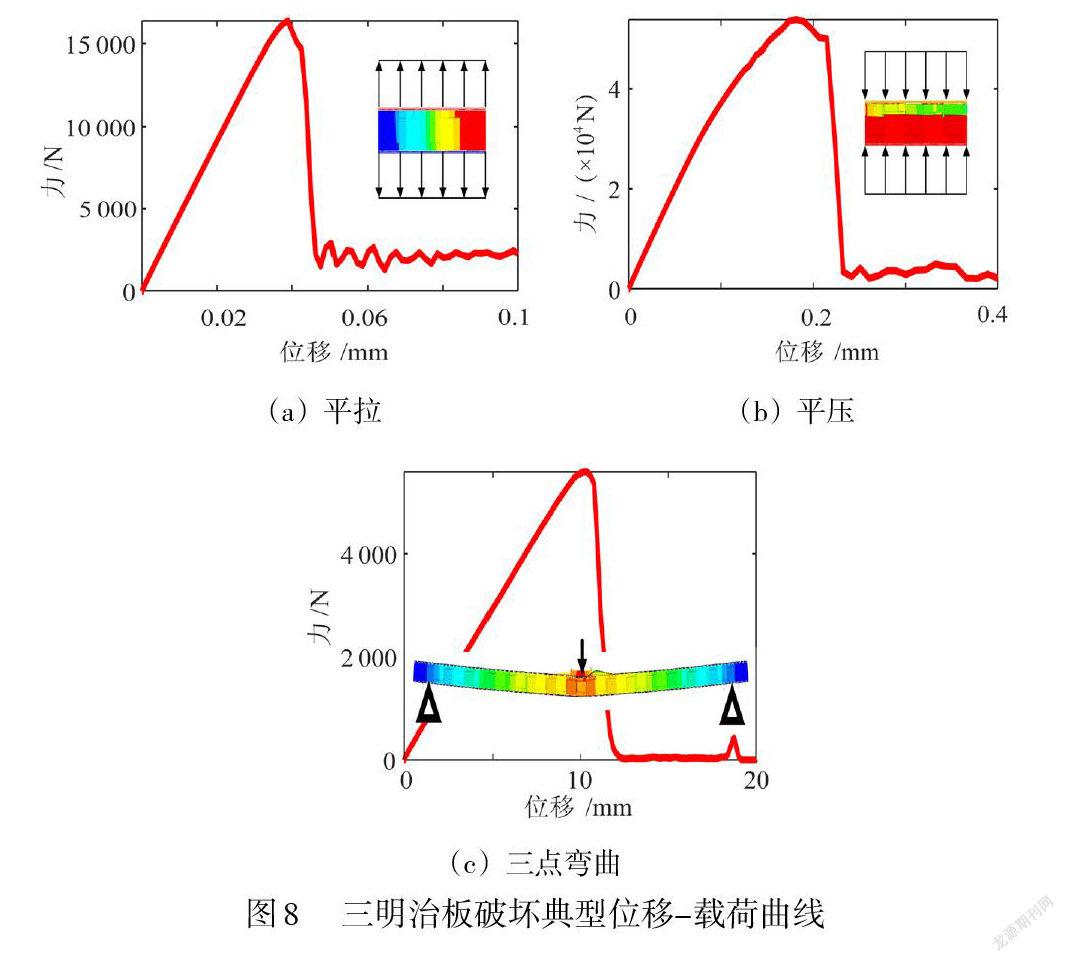
对于强度性能，根据三明治板不同工况下的破坏，如图8所示，定义平拉强度σT 为三明治板在受到平拉载荷下发生失效时的平均拉应力。平压强度σC 为三明治板在受到平压载荷下发生失效时的平均压应力。根据相关标准[20]，弯曲强度以三明治板破坏时的面板应力作为三明治板的弯曲强度，计算如下：

式中：σB 为面板中的拉压应力; Fb，max 为峰值载荷;a 为支座跨距;b 为试样宽度; tf 为面板厚度;V 为三明治板总厚度。

2.4 设计方案验证

为了说明第1节中所述方案对于提升拉伸强度的有效性，在所建立的平拉有限元模型基础上，计算了在蜂窝边长为18 mm ，蜂窝厚度为1.5 mm下，不同加强板宽与加强板厚组合下的平拉强度，并与没有加强板的蜂窝结构（ ws=0）的平拉强度进行了对比，如图9所示。总体看来，由于加强板的引入，相比于无加强板结构（图9底部），平拉强度得到了一定提升。但在加强板厚一定时，平拉强度随着加强板宽的增大而呈现出先增大后不变的现象，因此会出现粘接面积足够大，但粘接强度提升有限的情况，如此反而增加了无用的质量，不利于轻量化。故每个加强板厚都对应着一个最优的粘接面积，也即最优的加强板宽（图9中虚线）。平拉强度的变化说明了单纯增加粘接面积并不意味着一定能取得较好的平拉强度，还需要考虑加强板的厚度，这是由于平拉载荷靠蜂窝壁来传递，与蜂窝壁相连的加强板的刚度则决定了粘接面上拉伸应力的分布情况，加强板的刚度越大，则拉伸应力分布越均匀;因此在粘接面强度一定的情况下，由于应力分布均匀，达到最大应力的面积会比应力分布不均匀时大，宏观上合力也更大，相对来说平拉强度也会提高。所以在通过增大加强板宽度来提高粘接面积的同时，也需要增加加强板厚来增加刚度，才能达到提高平拉强度的目的。综上所述，第1节所提出的设计方案能够提高平拉强度，但需要考虑结构参数的组合以获得更好的效果。

3 基于轻量化与强度的蜂窝结构参数多目标优化

根据第2节的计算，本文提出的设计方案中的加强板厚和加强板宽对于平拉强度有显著影响。而蜂窝边长、蜂窝壁厚等结构参数对于三明治板的其他力学性能也有较大影响[21–24]。因此，为了更好地实现本文提出的蜂窝结构下三明治板的轻量化效果，需要对蜂窝结构参数进行调整，而同时要兼顾力学性能，因此构建了如下的多目标优化流程来完成蜂窝结构参数的求解。

为了兼顾力学性能与轻量化，需要对蜂窝的结构尺寸进行优化。如果同时考虑面密度和力学性能对设计变量进行优化，这是一个多目标优化问题。求解多目标优化问题的一个常用方法是转化为单目标优化问题：由于力学性能满足基本要求即可，所以把力学性能作为约束，将多目标问题转化为只对面密度进行优化的单目标优化问题。大致确定设计变量范围后，该优化问题可以表示为：

为了求解上述优化问题，搭建如图10所示的基于代理模型的蜂窝结构参数优化流程。所谓代理模型（或近似模型、元模型），即根据计算得到输入变量和输出响应后，使用一定的数学模型来描述输入和输出的关系，是实际模型的近似。在代理模型中，输入变量和输出响应之间的关系用下式描述：

式中： y（x）为实际响应值，是未知函数; （x）为近似响应值，是已知的数学模型，通常采用多项式;ε为近似值与实际值之间的随机误差。

基于代理模型优化的优点：能够在样本合适的情况下建立较为准确的近似模型以获得输入、输出的量化关系;在代理模型可信度足够的情况下，使用代理模型替代有限元模型能够大大减少有限元模型在环优化的耗时，提高优化效率[25]。

在已经建立的有限元模型基础上，本文的优化流程分为以下5个步骤：（1） 使用拉丁超立方在规定的设计变量范围内选取样本点，本文针对4个设计变量取150个点; （2）基于样本点中的尺寸参数进行有限元建模计算，得到不同尺寸组合下蜂窝三明治板的多工况力学性能响应;（3）根据所选样本点和得到的力学性能响应，采用多种代理模型近似算法建立代理模型;（4）比较不同代理模型近似算法，进行调整和修正，得到合适的代理模型;（5）基于最终的代理模型进行优化计算，得到优化后的设计方案。

根据选取的输入样本点以及有限元模型的计算结果，分别采用了 Kriging方法、RSM响应面模型以及径向基神经网络（Radial Basis Functions ， RBF ）进行对比。得到3种近似算法下近似模型的可信度指标 R2、標准均方根误差 NRMSE、标准最大绝对值误差 NMAE ，如图11所示。可信度指标 R2越接近1、标准均方根误差 NRMSE 和标准最大绝对值误差 NMAE 越接近0，表明代理模型越精确。结合图中的比较，综合来看，在当前的样本下，RSM要优于其他两种方法。故选择 RSM来生成代理模型。

由于当前优化问题中目标函数较为复杂，与设计变量之间的数学关系不明确。本文优化采用多岛遗传算法（Multi-Island Genetic Algorithm ， MIGA ）， MIGA 具有全局寻优能力以及天然并行性，效率相比于传统遗传算法有所提高[25]。

利用上述优化流程对蜂窝结构参数进行优化，得到优化解，将此组解圆整之后（l=14 mm ，t=1 mm ，ts=3 mm， ws=3 mm）代入有限元模型再次进行计算，对比原始设计（l=12 mm ，t=2 mm ，ts=1 mm ，ws=2 mm），两者的性能结果如图12所示。其中，平拉、平压（试样边长50 mm）以及三点弯曲的载荷-位移曲线如图13所示。结果表明，通过上述优化计算得到当前力学性能要求下蜂窝结构参数的最优组合。原始方案虽然在强度上有较大余量，但其面密度相应也比较高，优化后的三明治板平拉和平压强度有所降低，但仍然满足要求，弯曲强度和原始设计相当，而面密度相比于优化前降低了近30%。

优化结果表明，建立的优化流程正确，优化结果可信。基于多目标优化，在三明治板力学性能与轻量化之间取得平衡，使得三明治板既能够满足强度要求，又能够降低重量而达到轻量化的目的。

4 结束语

针对短纤维复合材料蜂窝三明治板，建立了计算平拉、平压、三点弯曲强度的有限元模型。提出了一种增大粘接面积的蜂窝设计方案，并基于有限元方法，计算验证了其在提高平拉强度方面的效果。从结构力学性能与轻量化出发，提出了一种考虑多强度的综合轻量化设计方法，构建用于蜂窝结构参数优化的代理模型并进行了优化分析，分析结果表明，所提出的短纤维复合材料蜂窝三明治板结构设计方案在满足强度要求的前提下，轻量化效果显著，具体如下。

（1） 考虑短纤维复合材料的脆性特性以及粘接强度问题，建立短纤维复合材料蜂窝三明治板精细化有限元模型，以此计算三明治板强度。

（2） 通过有限元模型的计算验证了所提出的增大粘接面积的蜂窝设计方案。新设计方案相比于无加强板蜂窝能够增大平拉强度，但除了增大粘接面积外，还需要增加蜂窝加强板刚度，能使平拉强度得到更好地提高。

（3） 基于有限元模型计算的样本点，通过比较 Krig? ing方法、响应面法和径向基神经网络所生成的代理模型的精度，确定选择误差较小的响应面法作为代理模型的生成算法。分析表明，采用响应面生成的代理模型可信度指标接近于1，精度较高。

（4） 以三明治板面密度为目标函数，将平拉、平压、弯曲强度作为约束条件，采用多岛遗传算法对蜂窝结构参数进行优化设计，优化后三明治板的面密度相比于优化前降低了30%，强度满足要求。

参考文献：

[1] FAN H，OUYANG J，SUN F，et al. Light-Weight Design of CRH Wind Deflector Panels based on Woven Textile Sandwich Com? posites[J]. Acta Mechanica Solida Sinica，2016，29（2）：208-220.

[2] TANG Y，HE W，XIN F，et al. Nonlinear sound absorption of ultra? light hybrid-cored sandwich panels[J]. Mechanical Systems and Signal Processing，2020（135）：106428.

[3] PROEN?A M，NEVES E SOUSA A，GARRIDO M，et al. Acoustic performance  of composite  sandwich  panels  for  building  floors： Experimental tests and numerical-analytical simulation[J]. Jour? nal of Building Engineering，2020（32）：101751.

[4] CRUPI V，EPASTO G，GUGLIELMINO E. Comparison of alumini? um  sandwiches for lightweight  ship  structures： Honeycomb  vs. foam[J]. Marine Structures，2013（30）：74-96.

[5] KOV?CS G，FARKAS J. Optimal design of a composite sandwich structure[J]. Science  and  Engineering  of  Composite  Materials， 2016，23（2）：237-243.

[6] KIM J S，JEONG J C. Natural frequency evaluation of a composite train  carbody with  length  of 23 m[J]. Composites  Science  and Technology，2006，66（13）：2272-2283.

[7] SEO S I，KIM J S，CHO S H. Development of a hybrid composite bodyshell  for  tilting  trains[J]. Proceedings  of the  Institution  of Mechanical Engineers，Part F： Journal of Rail and Rapid Transit， 2008（1）：1-13.

[8] WANG J，SHI C，YANG N，et al. Strength，stiffness，and panel peel? ing strength of carbon fiber-reinforced composite sandwich struc? tures with aluminum honeycomb cores for vehicle body[J]. Com? posite Structures，2018（184）：1189-1196.

[9] LASPALAS M，CRESPO C，JIM?NEZ M A，et al. Application of micromechanical models for elasticity and failure to short fibre reinforced  composites. Numerical  implementation  and  experi? mental   validation[J].  Computers   and   Structures，2008（9）：977-987.

[10]郭云竹.热塑性复合材料研究及其在航空领域中的应用[J].纤维复合材料，2016，33（3）：20-23.

[11] KOMAROV V A，KURKIN E I，CHARKVIANI R V. Increasing Aerospace Structures Strength Using Short Fiber Reinforcing[J]. Procedia Engineering，2017（185）：119-125.

[12] SAITO Y，FERNANDEZ F，TORTORELLI D A，et al. Experimen? tal  Validation  of  an  Additively  Manufactured  Stiffness-Opti? mized Short-Fiber Reinforced Composite Clevis Joint[J]. Exper? imental Mechanics，2019，59（6）：859-869.

[13] KURKIN E I，SADYKOVA V O. Application of Short Fiber Re? inforced Composite Materials Multilevel Model for Design of Ul? tra-light  Aerospace  Structures[J]. Procedia  Engineering，2017（185）：182-189.

[14] REJAB M R M，BACHTIAR D，SIREGAR J P，et al. The mechan? ical behavior of foam-filled corrugated core sandwich panels in lateral compression[C]//Proceedings of the American Society forComposites -31st Technical Conference，ASC 2016.

[15] XU X，JIANG Y，PUEH LEE H. Multi-objective optimal design of  sandwich  panels  using  a  genetic  algorithm[J]. Engineering Optimization，2017，49（10）：1665-1684.

[16] GARRIDO M，MADEIRA J F A，PROEN?A M，et al. Multi-ob? jective optimization of pultruded composite sandwich panels for building floor rehabilitation[J]. Construction and Building Mate? rials，2019（198）：465-478.

[17] LI X，LI G，WANG C H，et al. Optimum design of composite sand? wich structures subjected to combined torsion and bending loads [J]. Applied Composite Materials，2012， 19（3/4）：315-331.

[18] HASHIN Z. Failure criteria for unidirectional fiber composites [J]. Journal of Applied Mechanics，Transactions ASME，1980，47（2）：329–334.

[19] LIU  H，LIU J，DING Y，et  al. Modelling  damage  in fibre-rein? forced  thermoplastic  composite  laminates  subjected  to three-point  bend  loading[J]. Composite  Structures，2020（236）：111889.

[20] GB/T 1456-2005， 夹层结构弯曲性能试验方法[S].

[21] FU X，MEI Z Y，CHEN G T，et al. Research on the optimization design method of the stiffness of the composite sandwich panel [C]//IOP Conference Series： Materials Science and Engineering. Institute of Physics Publishing，2020.

[22]齐佳旗，段玥晨，铁瑛，等.结构参数对 CFRP蒙皮-铝蜂窝夹层板低速冲击性能的影响[J].复合材料学报，2020，37（6）：1352-1363.

[23] IVA?EZ  I，FERNANDEZ-CA?ADAS  L  M，SANCHEZ-SAEZ S. Compressive  deformation  and  energy-absorption  capability of  aluminium  honeycomb  core[J]. Composite  Structures，2017（174）：123-133.

[24] FAN H L，MENG F H，YANG W. Sandwich panels with Kagome lattice  cores  reinforced  by  carbon  fibers[J]. Composite  Struc? tures，2007，81（4）：533-539.

[25]赖宇阳. Isight参数优化理论与实例详解[M].北京：北京航空航天大学出版社，2012.

第一作者简介：岳科宇（1996-），男，四川人，硕士研究生，研究领域为轨道车辆部件强度与碳纤维材料结构设计。

※通讯作者简介：陆正刚（1966-），男，江苏人，博士，教授，研究领域为轨道车辆动力学与控制，已发表论文38篇。

（编辑：刁少华）