基于改进 EMD样本熵和 SVM的风机滚动轴承故障诊断

张韦 张永 骈晓琴 苏赫 蔺相东

摘要：风机齿轮箱振动信号成分复杂，而经验模态分解（ EMD ）在故障诊断中存在模态混叠和端点效应问题。针对此问题，研究了一种 EEMD 样本熵和高斯径向基核函数的 SVM分类器的滚动轴承故障诊断方法。以风机齿轮箱滚动轴承为研究对象，提取了内圈故障、外圈故障、滚动體故障和正常轴承4种状态振动信号，利用 EEMD和小波分别对振动信号分解降噪并筛选主要 IMF 分量;计算前4阶 IMF 分量的样本熵作为特征向量;最后将特征向量输入高斯径向基核函数的 SVM模型进行故障识别。结果表明：EEMD 算法对端点效应和模态混叠都有一定抑制作用，EEMD 样本熵和 SVM 相结合可有效识别滚动轴承故障类型，故障识别率为97.5%，为工程应用中风机齿轮箱滚动轴承故障诊断提供参考。

关键词：滚动轴承;EEMD 分解;样本熵;SVM;故障诊断

中图分类号：TH17             文献标志码：A

文章编号：1009-9492（2021）12-0038-04

开放科学（资源服务）标识码（OSID）：

Fault Diagnosis of Rolling Bearing Based on Improved EMD SampleEntropy and SVM

Zhang Wei1，Zhang Yong1，Pian Xiaoqin2，Su He1※，  Lin Xiangdong1

（1. School of Mechanical and Electrical Engineering， Inner Mongolia Agricultural University， Hohhot 010018， China;

2. Department of Hematology， Affiliated Hospital of Inner Mongolia Medical University， Hohhot 010050， China）

Abstract： The components of the vibration signal of the wind turbine （WT） gearbox are complex， and empirical mode decomposition （EMD） has problems of modal aliasing and end effect. Aiming at this problem， a rolling bearing fault diagnosis method based on EEMD sample entropy and Gaussian radial basis kernel function SVM was studied. Taking the rolling bearing of the wind turbine gearbox as the research object， the four state vibration signals of inner ring failure， outer ring failure， rolling element failure and normal bearing were extracted， and the vibration signals were decomposed and denoised respectively by EEMD and wavelet and the main IMF components were screened. The sample entropy of the first four-order IMF components was calculated as the feature vector. Finally， the feature vector was input into the SVM model of the Gaussian radial basis kernel function for fault identification. The results show that the EEMD algorithm has a certain inhibitory effect on the end effect and modal aliasing. The combination of EEMD sample entropy and SVM can effectively identify the type of rolling bearing fault， and the fault recognition rate is 97.5%， which provides a reference for the fault diagnosis of rolling bearing of WT gearbox in engineering application.

Key words： rolling bearing; EEMD decomposition; sample entropy; SVM; fault diagnosis

0 引言

风能作为一种无污染、可再生的绿色能源，近年来获得了井喷式发展，2018年风能累积量（GW）比2015年高出约43%[1]。由于风电机组运行环境极度恶劣，齿轮箱各部件故障频发，滚动轴承作为风电机组齿轮箱的关键旋转部件，也是最容易损坏的零件之一，而故障停机导致的维护成本非常高，因此轴承故障诊断技术越来越得到重视[2-4]，这对于保障机械装备的安全可靠运行、维护维修具有重要的工程实际意义。

经验模态分解 （Empirical  Mode  Decomposition， EMD ）是 Huang等[5]于1998年提出的一种自适应信号处理方法，其本身存在模态混叠和端点效应问题[1，6]。相关研究表明，间歇信号、脉冲信号和噪声信号等是引起模态混叠的主要原因。针对此问题，时培明等[7]结合相似极值延拓和加余弦窗函数运算的优点，提高了 EMD 方法的运算精度，与单一故障特性相比，诊断出了振动信号既有裂纹引起的高频成分，也有碰摩引起的低频成分。张雪英[8]提出峭度准则变分模态分解样本熵与概率神经网络的齿轮故障诊断方法，准确率达96.25%。Deering 等[9]通过添加掩膜信号法来均匀化原始信号的极值点分布，从而达到抑制模态混淆的目的。Wu Z H[10]将高斯白噪声叠加到原始信号，利用白噪声频率分布均匀性和均值为零的特点，将原始信号自适应地分布到相应的尺度上并通过多次平均消除噪声的影响。SMITH[11]提出局部均值分解（ LMD），可直接从若干有物理意义的瞬时频率乘积函数线性组合中同时获得多分量调幅调频信号，其解调过程不依赖于Hilbert变换，迭代收敛速度较快且端点效应得到改善。支持向量机（SVM）是一种适用于小样本分类、学习能力和分类能力较强的算法[12]。但长林等[13]基于完备集合经验模态分解提取样本熵，结合支持向量机实现滚动轴承的故障诊断。施莹等[14]基于集合经验模态分解提取排列熵，结合最小二乘支持向量机实现了对高速列车轮对轴承的故障诊断。ZHENG等[15]利用复合多尺度模糊熵构造故障特征的特征向量集合，并将其输入增强支持向量机，实现了轴承故障的高精度识别。

本文在相似极值延拓算法基础上改进 EMD ，延拓了信号两端极值点判断，有效控制了模态混叠问题。在搭建的模拟风机齿轮箱试验平台上模拟滚动轴承内圈故障、外圈故障、滚动体故障和正常4种状态，分别采集振动信号，用 EEMD 和小波对振动信号分解降噪并筛选主要 IMF 分量，计算前4阶 IMF 分量样本熵作为特征向量，再用高斯径向基核函数的 SVM分类方法进行不同类型滚动轴承故障识别。

1 经验模态分解改进算法及样本熵

针对原始经验模态分解算法存在的端点效应问题，通过添加辅助白噪声的方法，以消除模态混叠现象的影响。EMD 分解过程中，当信号端点为非极值点时，三次样条求包络线会拟合误差产生端点飞翼，且隨着迭代过程会延伸到信号内部，破坏数据，导致结果失真。本文采用的相似极值延拓法是提高 EMD 故障诊断准确性的新方法，首先对原始信号进行相似极值延拓处理，然后按照原信号长度去掉延拓部分，得到更准确的 IMF 分量。

设滚动轴承振动信号为：

式中： ti =t（i）Δt ， i=1， 2， 3， …， n ; n 为离散数据点数;Δt 为采样步长。

其极大、极小值对应的时间序列分别为 tmax （ i ），i=1， 2， 3， …， m 和 tmin （ i ），i=1， 2， 3， …， n 。以内部极值点序列均值将信号两端相邻的一对极大极小值时间差作为形状特征进行延拓。下面以左延拓算法为例说明该算法：

最终 EEMD 分解结果为：

式中：ci（t）为原始信号 x（t）的第 i 个IMF 分量;rn（t）为残余分量。

样本熵（ Sample Entropy ，SampEn）是由 Richman J S等[16]提出，从时间序列复杂性角度出发，衡量系统产生新模式的概率，定量描述系统的复杂度和规则度，样本熵数值越低，时间序列自我相似性就越高;数值越大，时间序列复杂度就越高。现将样本熵定义叙述如下。

（1） 将一时间序列 x（n）按序号组成 m 维向量序列，得到状态向量：

式中： 1≤i ≤N - m +1;Xm（i）为从第 i 点起 m 个连续x 值。

（2） 将Xm（ i ）和Xm（j ）两向量间距离定义为Dij：

式中：0≤k≤m-1。

（3） 设相似性容限 r ，统计Xm（i）和Xm（j）间距小于等于 r 的j （1计算所有平均值：

（4） 增加维数至 m+1，由 （1）～ （3），得：

（5）定义时间序列样本熵估计值为：

2 滚动轴承故障诊断流程

以风机齿轮箱滚动轴承为研究对象，实验模拟内圈故障、外圈故障、滚动体故障、正常轴承4种状态。由于实验室采集到的振动信号通常是多种信号的混合和叠加，除轴承本身的振动外，还有试验台振动产生的低频信号、周围环境产生的噪声信号等，这些信号都会影响故障特征的提取，因此对原始信号进行降噪处理，可以提高故障诊断的准确率，而小波降噪已被广泛应用到故障诊断领域，并取得了较好的效果[17-19]。具体故障诊断流程如图1所示。3 信号采集处理与特征向量提取

设定采样频率为1000 Hz ，转速 n=2500 r/min ，奈奎斯特因子设置为2.56，转速为2000 r/min ，分别在试验台 X、Y、Z 三个方向安装传感器采集正常轴承、内圈故障、外圈故障、滚动体故障4种状态振动信号，如图2所示。通过对比分析3个方向的振动信号，X 向测得较弱的径向信号，Z 向测得较弱的轴向信号，因此选取 Y 向较强的径向信号作为分析对象，4种类型振动信号的加速度波形及小波降噪后信号如图3～6所示。

从图3～5可知，试验台采集的原始信号含有大量噪声，且噪声频率较高，直接分析效果不好，须进行降噪处理;本文采用文献[18]提出的改进阈值小波降噪法，使用 Wavedec 函数进行降噪，降噪后信号更光滑、真实，高频信号明显减少，降噪效果明显。

以外圈故障为例，采用 EEMD 对上述降噪后信号进行分解，分解结果如图7所示。

经 EEMD分解后得到6个IMF 分量，如图7所示。各 IMF 分量包含了不同的时间特征尺度，轴承故障特征显示于以上时间尺度，IMF5和IMF6可看作自身算法不足产生的虚假模态。IMF1频率成分最高，并且出现了轻微震荡成分，反映外圈故障的冲击响应;IMF2～IMF4频率成分依次降低，IMF2、IMF3分量存在冲击信号特征，单周期性不明显;IMF2反映基频信号分量，两端未出现明显摆动，表明本文改进方法对端点效应和模态混叠有一定抑制作用。振动信号分解后，信号能量主要集中在前几个 IMF 分量中。选取训练集中3组样本为例，计算6个 IMF 分量与重构信号的相关因子，对各类轴承状态分解后的 IMF 分量取样本平均值，具体如表1所示。去掉相关因子小于0.01的 IMF 分量，本文选取前4个 IMF 分量，计算其样本熵作为特征向量。

4 不同类型滚动轴承故障类型的识别

为了准确识别滚动轴承故障类型，本文选取4种滚动轴承类型振动信号共计160组进行 SVM分类识别。其中，滚动轴承外圈故障、内圈故障、滚动体故障、正常轴承各40组。随机选取其中120组信号（每种类型30种）作为训练样本数据，将从中提取的特征向量作为 SVM分类器输入量，选用高斯径向基核函数参数和惩罚因子在2-10～210范围进行交叉验证的方法，训练和建立 SVM模型;其余40组信号（每种类型10组）作为测试样本数据，选用上述建立的 SVM模型和 svmpredict函数进行滚动轴承4种状态进行识别。

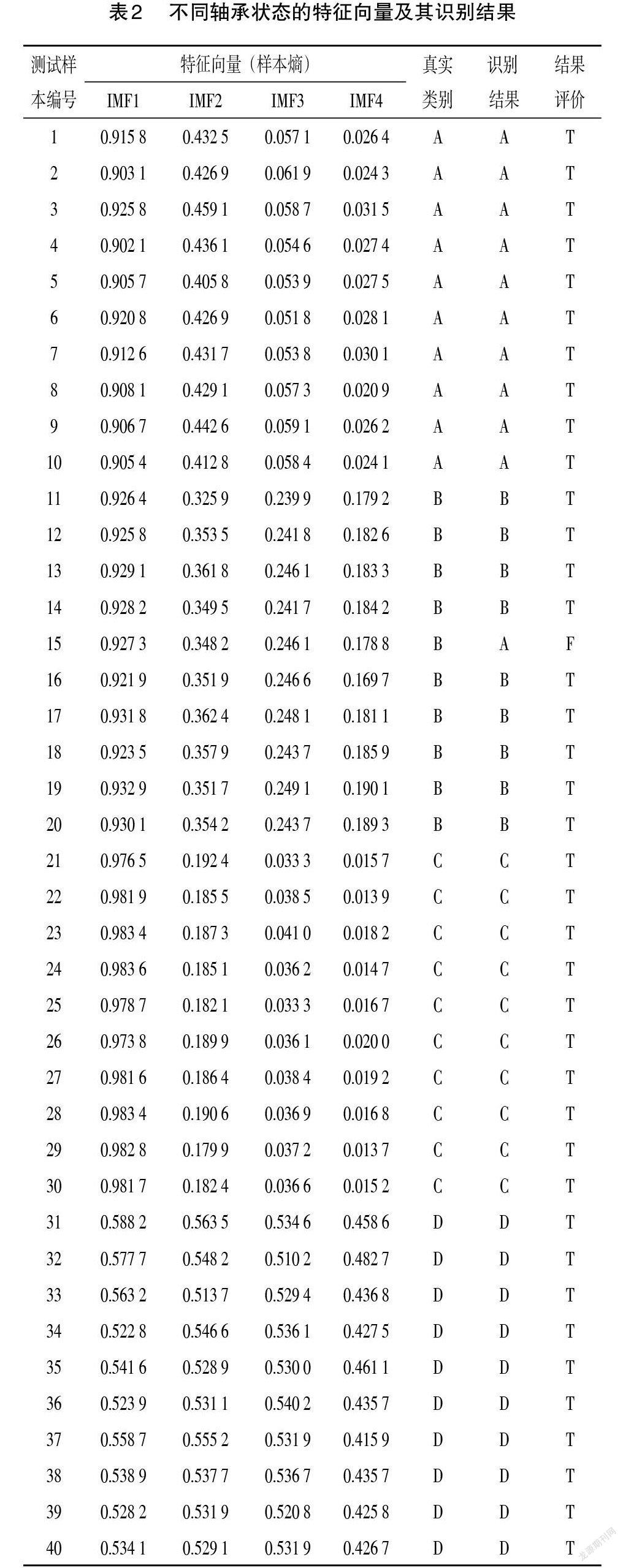
分别标记外圈故障、内圈故障、滚动体故障和正常轴承为 A、B、C、D ，40组测试样本的特征向量及其故障识别结果如表2所示。结果表明：40组测试样本中，外圈故障、滚动体故障、正常轴承识别结果全部正确;只有内圈故障识别中第15组样本识别错误，识别率为97.5%。

5 结束语

（1） 针对 EMD 方法存在的模态混叠和端点效应问题，在相似极值延拓算法的基础上改进 EMD ，延拓了信号两端极值点判断，开发了一种 EEMD 信号分解方法，并将滚动轴承4种状态振动信号分解，完成 IMF 分量筛选。

（2） 筛选并计算前4个 IMF 分量样本熵作为特征向量对 SVM进行训练，构建了 SVM智能识别模型。

（3） 采用测试样本对训练好的 SVM模型的识别精度进行测试，结果表明：该 SVM模型能较好地完成故障识别，识别率达97.5%。

参考文献：

[1] World Wind Energy Association.WWEA half-year report：world wind  capacity  reached 456 GW[EB/OL].（2016-10）.http：//www. wwindea.org.

[2] 王晓冬，何正嘉，訾艳阳.滚动轴承故障诊断的多小波谱峭度方法[J].西安交通大学学报， 2010， 44（3）：77-81.

[3] 皮骏，马圣，杜旭博，等.基于BQGA-ELM网络在滚动轴承故障诊断中的应用研究[J].振动与冲击，2019，38（18）：192-200.

[4] 郑一珍，牛蔺楷，熊晓燕.基于EMD-SDP特征融合的CNN轴承保持架故障诊断研究[J].机电工程，2021，38（1）：81-87.

[5] Huang N E， Shen Z，Long S R， et al. The empirical mode decom? position and the Hilbert spectrum for nonlinear and non-station? ary time series analysis[J]. Proceedings of the Royal Society of London，Series A， 1998（454）： 679-699.

[6] Gai G H. The processing of rotor startup signals based on empiri? cal mode decomposition[J].Mechanical Systems and Signal Pro? cessing，2006（20）：225-235.

[7] 时培明，李庚，韩东颖.基于改进EMD的旋转机械耦合故障诊断方法研究[J].中国机械工程，2013，24（17）：2367-2372.

[8]张雪英，刘秀丽，栾忠权.基于峭度准则 VMD 样本熵与 PNN 的齿轮故障诊断[J].组合机床与自动化加工技术，2018（9）：61-64.

[9] Deering R，Kaiser J F.The use of masking signal to improve empri? cal mode decomposition [C]//IEEE International Conference on Acoustics，Speech，and Signal Processing.Philadelphia，USA，2005.

[10] WU Z，HUANG N E.Ensemble empirical mode decomposition：A noise-assisted data analysis method[J].Advances in Adaptive Data Analysis，2009（1）：1-41.

[11] SMITH J S.The Local Mean Decomposition and Its Application to EEG Perception Data[J].Journal of the Royal Society Inter? face，2005，2（5）：443-454.

[12] CHENG J，YU D，Tang J，et al.Application of SVM and SVD tech? nique based on EMD to the fault diagnosis of the rotating ma? chinery[J].Shock & Vibration，2013，16（1） ： 89-98.

[13] 但长林，李三雁，张彬. 基于样本熵和SVM的滚动轴承故障诊断方法研究[J].中国测试，2020， 46（11）：37-42.

[14] 施莹，庄哲，林建辉.基于EEMD排列熵的高速列车轮对轴承故障诊断方法[J].中国测试， 2017， 43（11）： 89-95.

[15] ZHENG J D，PAN H Y，CHENG J S.Rolling Bearing Fault Detec? tion and Diagnosis Based on Composite Multiscale Fuzzy Entro? py and Ensemble Support Vector machines[J].Mechanical Sys? tems and Signal Processing，2017（85）：746-759.

[16] Richman J S， Moorman J R.Physiological time-series analysis using approximate entropy and sample entropy[J].American Journal of Physiology：Heart and Circulatory Physiology，2000， 278（6）：2039-2049.

[17]丁小健，周健，梁超，等.基于小波降噪和共振解调法的异步电机故障诊断方法[J].电机与控制应用，2020，47（9）：106-110.

[18]傅成豪，潘庭龙.基于改进阈值的风机齿轮箱故障信号小波去噪方法研究[J].可再生能源，2020，38（9）：1197-1202.

[19]樊高瞻，周俊，朱昆莉.基于改进形态-小波阈值降噪的轴承复合故障声学诊断[J].振动与冲击，2020，39（12）：221-226.

第一作者简介：张韦（1988-），男，河北张家口人，硕士，助教，研究领域为信号检测与处理。

※通讯作者简介：苏赫（1989-），男，博士，講师，研究领域为农业工程测试与控制。

（编辑：王智圣）