基于CFD的注采管柱接头修复胶液渗流规律研究*
2021-08-20徐长峰王建军陈月娥李新宏
徐长峰,赵 楠,王建军,陈月娥,李新宏
(1.中国石油新疆油田分公司呼图壁储气库作业区,新疆 呼图壁 831200;2.中国石油集团石油管工程技术研究院 石油管材及装备材料服役行为与结构安全国家重点实验室,陕西 西安 710077;3.西安建筑科技大学 资源工程学院,陕西 西安 710055)
0 引言
由于储气库在生产过程中要周期性地注入和采出天然气,使得注采井管柱受到周期性应力变化的影响,其在服役过程中可能会发生疲劳损坏、油管丝扣泄漏、螺纹失效、内外表面腐蚀、裂纹、磨损等失效问题[1-2]。2015年美国加利福尼亚州阿里索储气库管柱失效导致气体泄漏事故,造成直接经济损失约3.3亿美元[3]。常规的注采管柱均采用螺纹连接,据统计,约有80%的注采管柱失效都发生在螺纹连接部位。现场取样和工程测井表明,管柱丝扣微漏导致呼图壁储气库2口井出现套管带压问题。对注采管柱螺纹失效部分进行维修,对保证注采油管柱正常作业非常重要[4-5]。常规的管柱维修方法包括补贴修复、整形修复和膨胀管修复等[6]。注胶方法作为一种新的维修技术,在注采管柱修复方面尚处于初步探索阶段。因此,有必要研究注胶修复过程中的胶液渗流规律,为注胶修复技术的实际应用提供有力支撑。
当前国内外在油气井管柱注胶修复技术领域开展了一定的研究,主要包括抗高温高压堵漏剂研发以及堵漏剂在油气井屏障失效修复中的应用[7]。Liu等[8]研究了一种能够有效封堵高渗透层及提高堵漏率的高温凝胶堵漏剂;在耐高温性能的基础上,Qin等[9]提出了将AMPS引入凝胶堵漏剂中以提高储层条件下凝胶堵漏剂的耐盐性和耐温性;赵玲莉等[10]研发了能够成功适用于稠油热采井套管补漏问题的有优良低温和高温性能的化学堵漏剂(XP-3);郭永宾等[11]研发了一种满足不同尺寸级配漏失通道的抗高温可降解聚合物凝胶堵漏剂P(AM-DGCL);刘政等[12]针对孔隙性渗透漏失及裂缝性漏失问题研发一种亲油型高分子聚合物材料的油基膨胀型堵漏剂DHF系列。
油管螺纹失效区别于套管损坏,油管螺纹失效形成的通道通常不足1 mm,是1条非常狭小的缝隙。目前鲜有胶液在油管螺纹渗流机理相关的研究报道,本文拟采用计算流体动力学方法构建注胶修复过程中胶液在螺纹缝隙内渗流的数值仿真模型,研究胶液在螺纹缝隙内的渗流过程,揭示注胶压力、胶液密度、螺纹失效缝隙与胶液渗流深度之间的关系,从而为注采管柱注胶修复技术方案设计和工程实践提供理论支持。
1 注采管柱接头螺纹渗流修复胶体流动数学模型
胶体在管柱接头螺纹缝隙中的流动涉及胶体和气体的气液两相物质运动。采用欧拉多相流模型对胶体在管柱接头螺纹缝隙中的渗流流动过程进行建模,追踪胶体和气体之间的两相自由界面。欧拉-欧拉流体体积模型是一种欧拉网格下的自由表面追踪方法,认为计算域内是相互贯穿的流体,且不同流体之间互不相容。通过体积率描述不同相流体的空间分布,各相流体的体积率总和为1,运用几何重构方法对不同相流体作用界面进行追踪,在欧拉框架下胶体渗流过程中服从质量、动量和能量守恒[13-14],如式(1)~(3)所示:

(1)
(2)

(3)
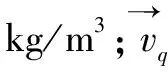
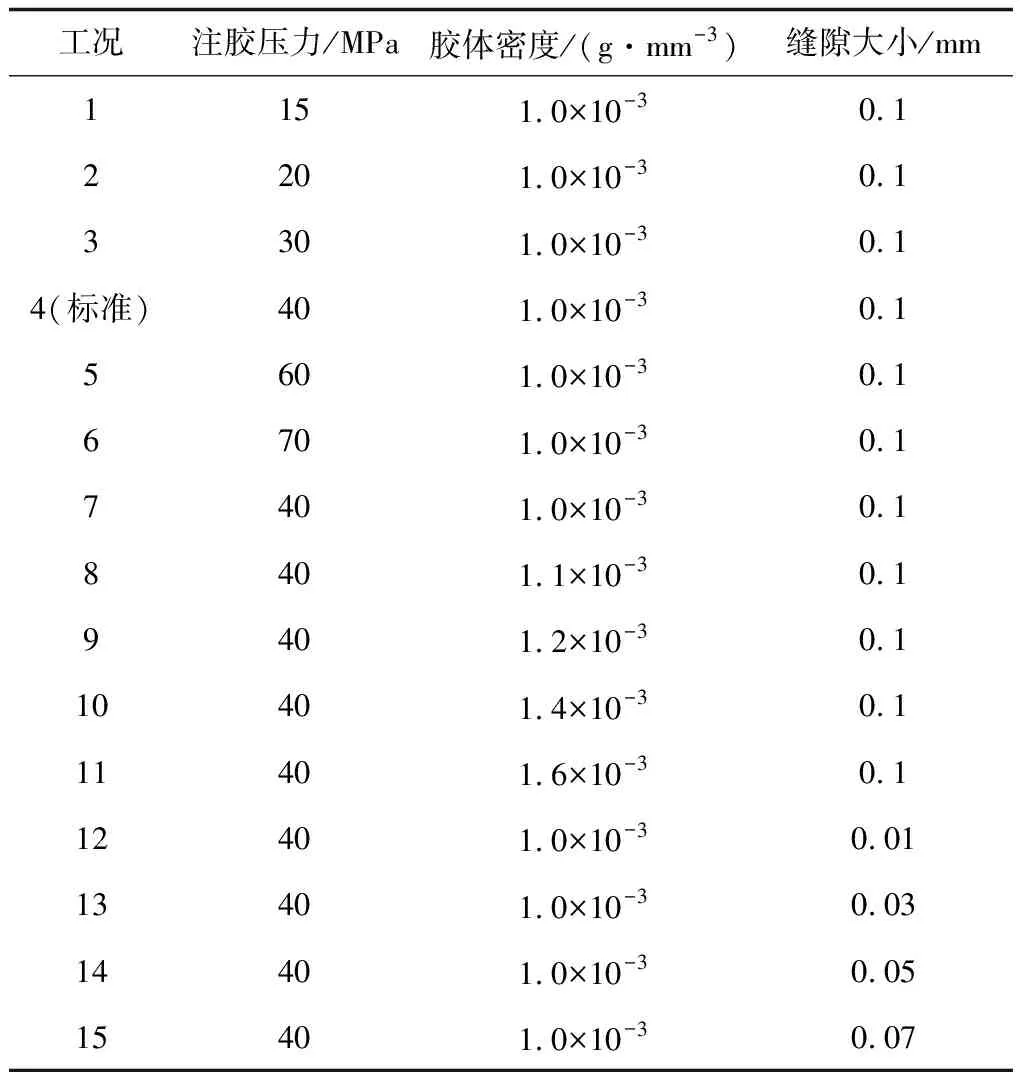
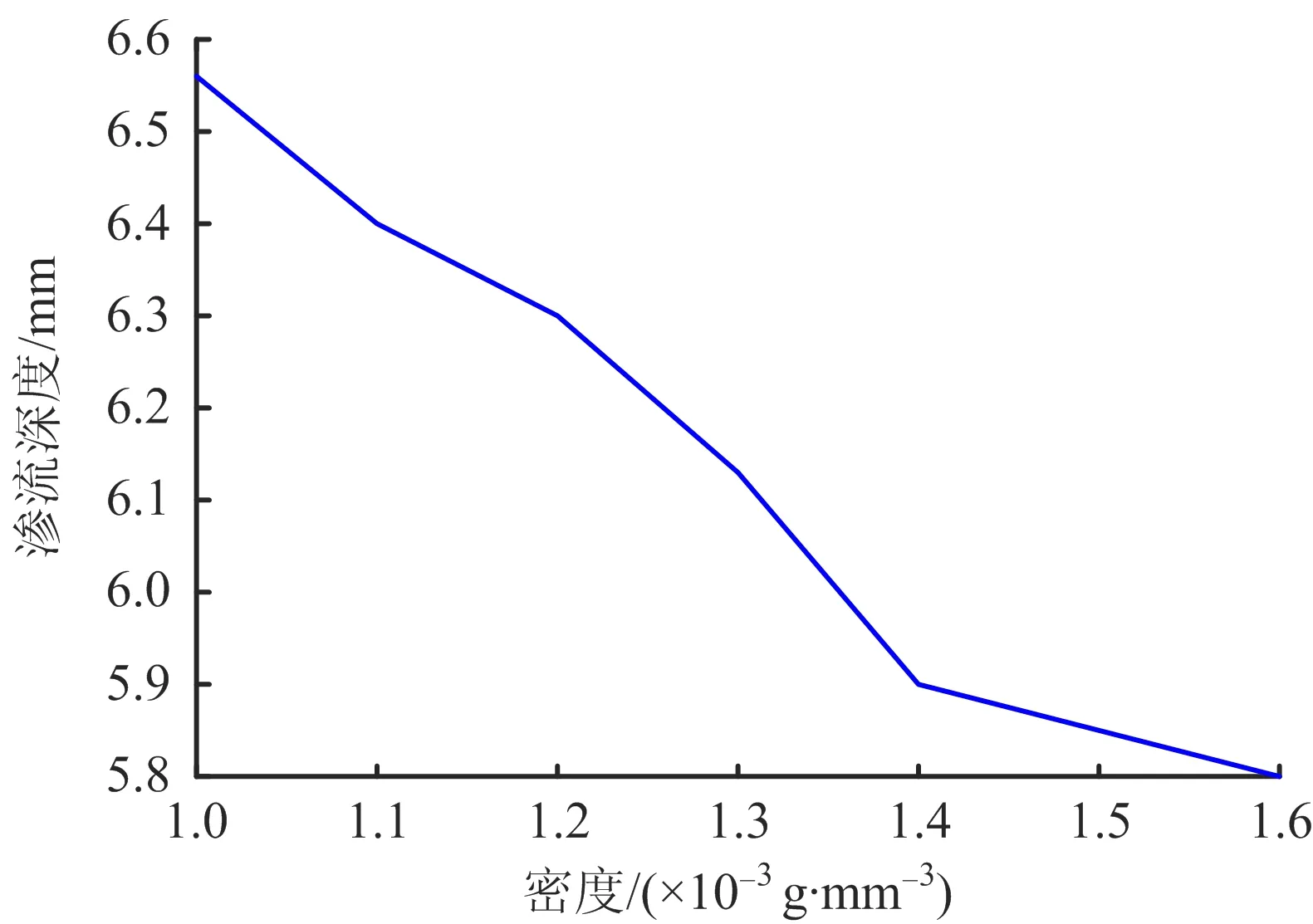
欧拉-欧拉多相流模型引入体积分数aq用于表示第q相所占的百分比。aq=0表示单元内第q相物质为空;0 (4) (5) 式中:aq为第q相的体积分数;t为时间项;x,y为坐标方向;u,v分别为x,y方向的速度。 引入湍流方程描述胶体流动的湍流特性,并使得基本控制方程封闭。可实现的κ~ε模型被证实具有较好的预测精度,输运方程如式(6)~(8)所示[15]: (6) (7) (8) 式中:κ为湍流动能;ε为湍流动能耗散率;σκ、σε分别为κ和ε的湍流Prandtl数;C2和C1ε为常数;xj、uj分别为坐标轴和速度分量;Gκ和Gb分别为平均速度梯度和浮力作用产生的湍流动能;C3ε为浮力对湍动耗散率的影响程度;YM为可压湍流的波动扩张对整体耗散率的贡献;Sij为平均应变率张量;Sκ和Sε为用户自定义源项。 注采管柱管体规格φ114.3 mm×7.37 mm,注胶施工压力为40 MPa,图1为注采管柱的螺纹缝隙示意图,螺纹缝隙尺寸在0.01~0.1 mm之间。基于螺纹缝隙的几何尺寸,对缝隙外部轮廓进行简化处理,仅对胶体流动的螺纹缝隙通道进行建模,并进行网格划分,如图2所示。 图1 油管螺纹缝隙示意 图2 螺纹缝隙物理模型 螺纹缝隙壁面采用无滑移边界条件,针对螺纹缝隙出口封闭和不封闭2种状态,分别采用墙面wall和压力出口表征上述2种缝隙出口状态;由于采用高压进行胶液注射,因此螺纹缝隙入口采用压力入口边界条件,定义注胶驱动压力。认为螺纹缝隙在初始状态下充满甲烷气体,缝隙内的初始压力为10 MPa,然后分别改变入口压力条件,进行胶体流动过程模拟,甲烷气体的密度服从理想气体状态方程。在实际工况中,采用WS-711低黏度高强粘性树脂进行螺纹缝隙修复,该胶体的黏度在450~700 cPa·s之间,密度为1.0×10-3~1.6×10-3g/mm3。 采用非稳态压力基求解器,在计算模型中启动隐式体积力公式来部分平衡压力梯度和动量方程中的体积力,以提高重力场中仿真模型的稳定性。控制方程离散采用有限体积方法,空间离散采用二阶迎风格式,时间离散采用一阶隐式积分法,对流项离散采用二阶迎风格式,扩散项离散采用中心差分格式,压力速度耦合求解采用PISO算法。 注采管柱螺纹缝隙内充满天然气,缝隙内的初始压力为10 MPa,螺纹缝隙尺寸的变化范围0.01~0.1 mm;采用一定的压力将低黏度高强粘接树脂注入螺纹缝隙内进行泄漏修复;基于构建的渗流数值仿真模型,研究注胶压力、胶体密度、缝隙大小及渗流深度之间的关系。基于操作压力、胶体特性和缝隙大小的变化,如表1所示。 以表1中的标准修复工况(螺纹缝隙为0.1 mm,胶液密度为1.0×10-3g/mm3,注胶压力为40 MPa)为例,图3为管柱接头螺纹狭缝内胶液的渗流过程,图中压缩空气与胶液位置如箭头所指。据图3可知,随着时间增长,在注胶压力的驱动下,胶液在管柱接头螺纹狭缝内的渗流深度逐渐增大。总体上,胶液渗流进入狭缝的时间极快,约1 000 μs时,胶液渗流深度达到该注胶压力下的极限深度。由于狭缝末端处于完全封闭的状态,主要靠注胶压力压缩螺纹缝隙腔体内的空气,形成空间,胶液才能够进入螺纹狭缝内。当螺纹狭缝内外压力达到平衡状态时候,胶液运动停止,此可胶液的渗流深度为该注胶压力条件下的极限渗流深度。 图3 管柱接头缝隙内胶液渗流过程 表1 注胶修复工况设定 图4为不同工作压力条件下螺纹缝隙内的胶液与气体稳态相界面分布。进行注采管柱螺纹修复所采用的工作压力不能超过管体抗内压强度的85%(72.7 MPa),因此本文所采用的最大工作压力为70 MPa。研究螺纹缝隙为0.1 mm,胶液密度为1.0×10-3g/mm3条件下,注胶压力对胶液渗流深度的影响。在螺纹封闭的情况下,工作压力对缝隙内的原始气体进行挤压形成空间,从而使得胶液流动进入缝隙内。如图4可知,随着工作压力的上升,胶液在管柱接头螺纹缝隙内的渗流深度逐渐增大。这主要是由于随着工作压力增大,能够对螺纹缝隙内的原始气体进一步压缩,使其体积进一步减小,从而更大的工作压力条件下胶液的渗流深度更大。渗流深度随注胶压力的变化规律如图5所示。 图4 不同操作压力条件下螺纹缝隙内胶液与气体稳态相界面分布 图5 渗流深度随注胶体压力的变化 图6为不同胶体密度条件下螺纹缝隙内胶液与气体的稳态相界面分布。密度主要影响胶液的密度,根据调研资料胶液的密度一般在1.0×10-3~1.6×10-3g/mm3之间。因此,对螺纹缝隙尺寸0.1 mm、注胶压力为40 MPa条件下的胶体在缝隙内的渗流过程进行计算。胶体密度主要影响胶体的可流动性,密度越大的胶体在渗流过程中受到的摩擦阻力和压差阻力越强,因此在相同压力条件下进入缝隙内的长度越短,胶体渗流深度随胶液密度的变化规律如图6所示。但基于计算结果,密度变化所引起渗流深度的变化量较小。 图6 渗流深度随胶体密度的变化关系 管柱接头螺纹缝隙尺寸具有随机性,不同失效工况对应的螺纹缝隙宽度不同,考虑缝隙尺寸在0.01~0.1 mm之间变化,研究40 MPa注胶压力条件下,胶体密度为1.0×10-3g/mm3时,胶体渗流深度随螺纹缝隙尺寸的变化。螺纹缝隙尺寸越小,胶体在狭缝内渗流所受到的压差阻力越大,在胶体进入缝隙内进行延展性渗流的难度越大。如图7所示,螺纹缝隙较大时的胶液渗流深度略大于螺纹缝隙较小时的工况,但缝隙变化所引起的渗流深度变化量总体较小,如图7所示。 图7 渗流深度随缝隙尺寸的变化关系 1)采用计算流体动力学欧拉-欧拉多相流方法构建了油管柱接头螺纹缝隙内胶液渗流分析模型,以胶体渗流过程中与螺纹狭缝内原有气体的两相自由相界面追踪和表征胶液渗流深度,根据管柱接头螺纹狭缝几何尺寸建立胶液渗流物理模型,实现对0.01~0.1 mm螺纹接头缝隙注胶修复过程分析。 2)胶液在狭缝内的渗流深度与注胶压力呈正比,当注胶压力达到70 MPa时,胶液在螺纹缝隙近水平缝隙内的渗流深度能达到8 mm;胶液渗流深度与胶液密度呈反比,密度增大会增加胶液在螺纹狭缝内渗流的摩擦阻力和压差阻力,从而渗流深度随着密度增大而减小;胶液渗流深度与螺纹缝隙尺寸呈正比,螺纹缝隙尺寸增大会降低胶液在狭缝内的表面张力和摩阻,从而胶液渗流深度随着螺纹缝隙的增大而增大;胶液渗流规律可为注采管柱注胶修复技术方案设计和工程实践提供理论支持。2 注采管柱接头螺纹渗流修复胶体流动仿真模型


3 结果与讨论
3.1 注胶修复工况
3.2 管柱接头缝隙内胶液渗流过程
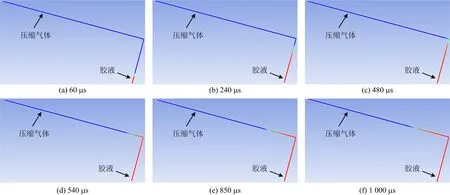
3.3 注胶压力对渗流深度的影响

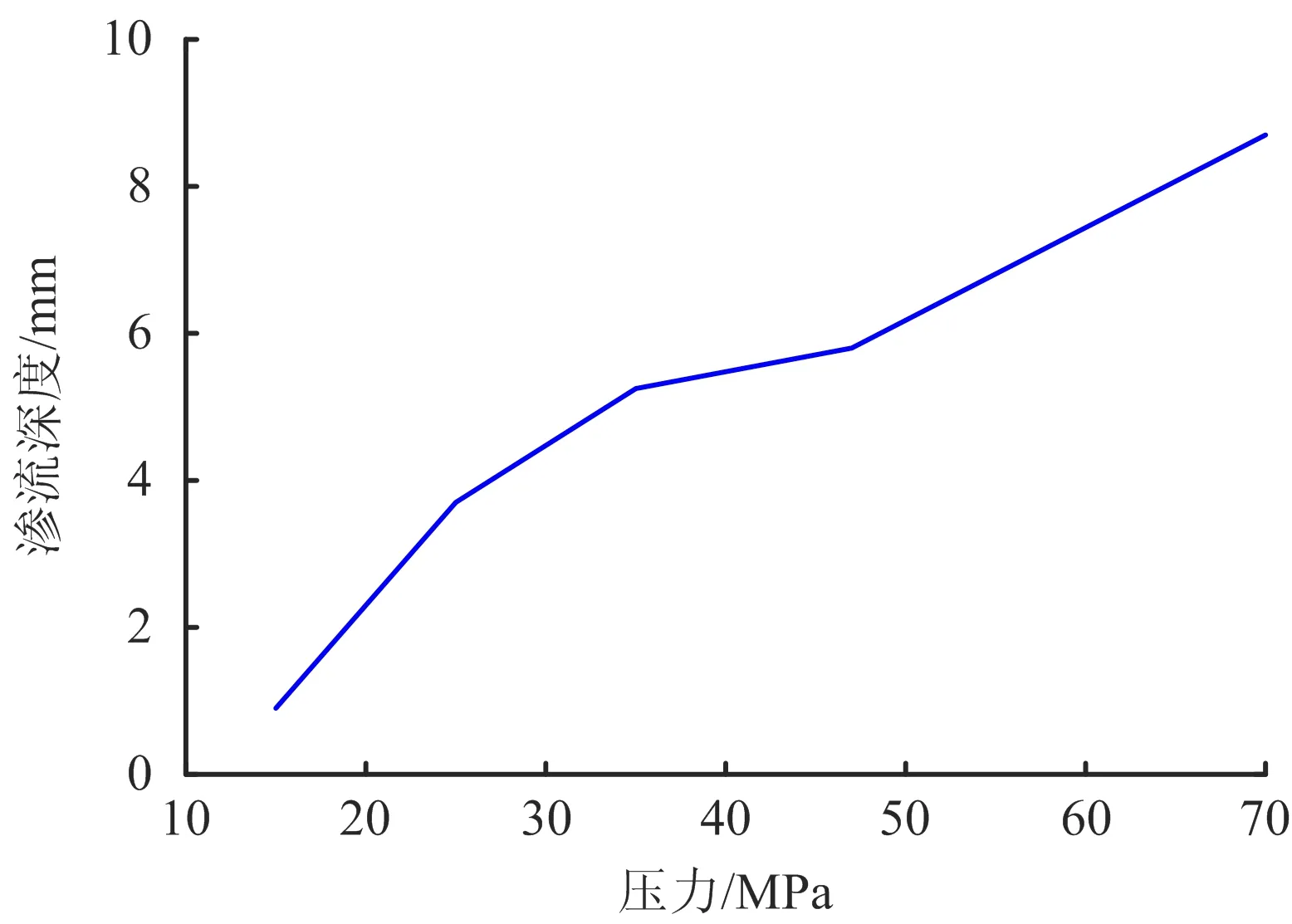
3.4 密度对胶体渗流深度的影响
3.5 螺纹缝隙尺寸对胶体渗流深度的影响

4 结论
