基于滚动模糊时间窗的场面动态路径规划

谢春生，卢菲菲，杨群亭

(中国民航大学空中交通管理学院，天津 300300)

随着民航业的蓬勃发展，机场航班量不断增加，机场场面拥堵问题日益突显，成为制约机场运行效率与安全水平的关键因素。因此合理规划机场场面滑行路径，对于机场发展具有重大意义。

关于机场地面滑行问题，迄今已有多位学者展开相关研究。传统算法方面，谷润平等[1]使用改进的 D* 算法研究场面动态滑行问题；李睿馨[2]运用Dijkstra算法构建多因素约束的滑行路径模型优化机场场面滑行路径；刘帆等[3]建立机场路网有向图，并使用 A*算法进行场面滑行动态规划求解。智能算法方面；姜雨等[4]构建场面航空器滑行时空协同优化模型，基于遗传算法研究滑行成本与滑行冲突对场面航空器滑行路径的影响；冯程等[5]设计了基于禁忌搜索算法的优化模型，研究滑行路径规划与停机位分配联合问题的解决方法。建模方面，Xiao等[6]提出面向彩色滑行道Petri网模型以解决基于先进场面活动引导和控制系统(advanced surface movement guidance and control system，A-SMGCS)的飞机无冲突滑行路线规划问题；赵天宇等[7]提出冲突解脱策略并基于航空器油耗最小的无冲突路径规划算法对场面滑行问题求解；沈建凯等[8]基于 Q 学习对管制员管制行为建模，检测冲突集合并预估冲突，提前预判分配路线避让冲突得到最优滑行路径。以上研究从成本、冲突等方面研究滑行路径规划问题，却未探究机场运行中滑行时间不确定对路径规划造成的影响，而解决滑行时间不确定问题对路径规划和提高机场的运行效率均具有重要意义。

在基于模糊规则系统的基础上，现构建机场滑行时间预测模型，将滚动时间窗和模糊时间窗算法相结合，对滑行路径进行动态优化，以期降低机场地面滑行冲突，提高机场运行效率与安全水平。

1 基于 Mamdani 模糊规则系统的滚动模糊时间窗口算法

1.1 Mamdani模糊规则系统

(1)

本节聚焦机场地面滑行路线优化问题，基于此系统相关数据输入和输出的模糊集，以语言变量解释基础系统的形式模拟预测机场不同运行场景中的滑行时间。将这些解释变量输入与之相关的隶属度函数，模糊化后导入推理单元；在推理单元中赋予推理规则并设置聚合方法将输入映射至输出模糊集中；基于去模糊化运算方法获得量化数值，进而描述机场不同运行场景中滑行时间的状态。Mamdani-FBRS预测滑行时间的输入主要包括以下5个解释变量：总滑行距离、总转弯角度、进离场类型(二进制值0/1)、机场交通量和跑道的运行模式[9]。

总滑行距离DS：指在停机位和跑道之间航空器滑行的距离。

总转弯角度AS：以最短路径上相邻弧线之间的总角偏差计算。滑行速度是由航空器必须实现的总转弯量所限制的，总转弯量越大，滑行速度越慢。

进离场类型(二进制值0/1)：进场航空器为0，离场航空器为1。

机场的交通量N/Q：分为两大类：在某个时间段场面上正在移动的航空器数量N和停止移动的航空器数量为Q。其中，NA为场面上滑行的移动航空器中进场航空器的数量；ND为场面上滑行的移动航空器中离场航空器的数量；QA为场面上停止航空器中进场航空器的数量；QD为场面上停止航空器中离场航空器的数量。

跑道的运行模式：包括隔离运行和独立运行。

输出变量包括总滑行时间TS、等待时间TH和冲突次数NB。

基于Mamdani-FBRS[9]系统构建机场场面滑行模型，利用数据驱动提供航空器的滑行时间估值，先从包含航空器运动的历史数据集中识别并获取隶属函数参数的初始值，结合K-means算法与遗传算法[10]，后通过误差反向传播算法[11]加以调整，以达到提高Mamdani-FBRS的估算精度，从而形成自适应的Mamdani-FBRS，以达到更好预测模糊滑行时间的目的。对于机场场面滑行中的不确定性，通过航空器穿越机场布局图上某条滑行道的模糊时间，借助不同的λ量化机场滑行中的不确定性，且通过文中定义能近似表示模糊集Bi的隶属函数，进一步量化不确定性，达到更好的动态优化滑行路线的目的。

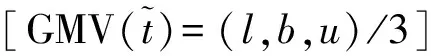
1.2 滚动模糊时间窗算法

滚动模糊时间窗算法首先对航空器次序采用滚动窗口进行预处理，基于Ravizza等[12]的算法基础，给定航空器ai的滑行请求Qi=(Vstart,Vend,τrw)，其中，τrw为机场分配给该航空进入跑道的时刻。在G上找到从顶点Vstart到终点Vend的无冲突路线Ri，且满足时间窗口最小滑行时间T的要求。算法找到通往终点节点的路线Ri就会终止，并将Ri分配给航空器ai。算法中用到的变量参数如表1所示。

表1 变量汇总

在运行中，机场基本按照先到先服务的原则(first come first service，FCFS)为飞机排序。为有效利用机场场面滑行资源，本节采用滚动窗口为航空器分配相应的滑行次序，在一定程度上减少航空器等待、延误时间及停止次数，以提高机场的运行效率。

滚动窗口考虑w架航空器等待，独立于所使用的最短路径算法，对航空器的排列进行单独搜索，并根据不同的潜在顺序为航空器分配滑行路线[13]。检查窗口内w个航空器的排列组合，所有排列组合里的航空器1～w都将被考虑且分配路线。按照每个组合所规定的顺序，从中选择最快的航空器滑行路线组合，并使其固定。之后窗口滚动到航空器w+1～2w，在此范围内，考虑航空器的所有排列组合，同时考虑先前航空器的路线。依次进行，窗口每次向前滚动w架航空器，并将路线分配给航空器，然后将其固定，同时使后续航空器避开先前航空器。假定航空器分配的使用跑道时间是固定的。在滚动窗口的基础上，再采用模糊时间窗算法对航空器的路线进行动态调整，找到航空器从起始点到终点的更优化路径。模糊时间算法步骤如下。

(1)设置H,ψ(v)=∅；∀v∈V创建一个新标签L=(Vstart,τrw,nil)。

(2)将带有τrw的标签L分别存储在H和集合ψ(vstart)中。

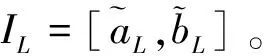
(4)如果VL=Vend，从L开始向前搜索重构Vstart到Vend的路线并存储在R，算法结束。

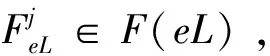
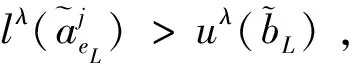
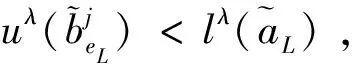
(8)对于R的起始第一条滑行道eL，设置πin=∅，初始化起始时间，πin←τstart。

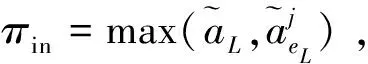
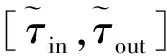
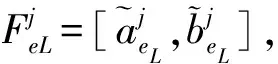
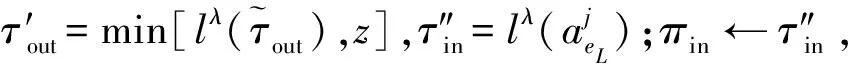
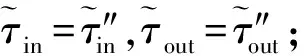
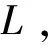
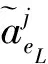
1.3 离场航空器滑行路线

针对离场航空器的滑行路线，滚动模糊时间窗算法在开始执行搜索离场航空器的滑行路线时，与进场航空器不同，它是从停机位开始往前搜索路径，通过跑道时间τrw和滑行时间来确定航空器的机位推出时间。本节假定跑道时间τrw为开始时间τstart(航空器从停机位开始滑行的时刻)减去航空器估计的滑行时间，滑行时间是从机位到跑道的最短路径的时间(使用经典的Dijkstra算法计算)。而针对用于分配路线的航空器推出时间τout，只考虑模糊集的模态值(即最大值)，故基于二分法迭代来确定航空器的最晚推出时间，旨在找到一条可行的路线Ri，其中航空器的推出时间在航空器分配的跑道时间之前，使航空器停在机位上的时间较长，以达到节约燃油和滑行进程中等待时间。

使用滚动模糊时间窗算法搜索滑行路线的进程中，若算法未能搜索到滑行路线，则直接将τstart减去10 min作为推出时间。如果能搜索到滑行路径且τout比τrw晚时，若搜索不到最佳路径Rbest，则将τstart提前τrw-τout差值tinc作为推出时间；若能找到最佳路径Rbest，则只需给τstart提前τrw-τout差值tinc的1/2作为推出时间。若能找到最佳路径Rbest且τout比τrw早，那么τstart就推后τout-τrw差值tinc的1/2作为推出时间。重复上述搜索滑行路径的进程，直至τout≡τrw或者达到规定的循环次数，最后找到Rbest或者没有滑行路径Ri。具体流程图如图1所示。

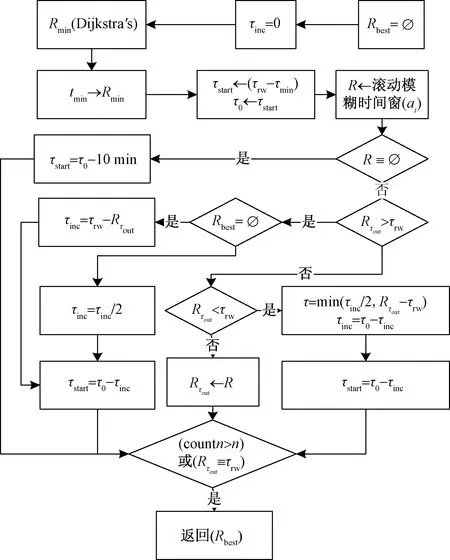
图1 离场路径搜索流程

2 机场运行模型设计

机场布局用有向图G=(V,E)表示，滑行道E代表滑行道，顶点V代表停机位、交叉点和中间点。一条滑行道e∈E有一组权值Te，表示穿越滑行道e的时间。对于某一架特定航空器的滑行时间teL∈Te取决于先前滑行的滑行道、机场运行模式和航空器进离港类型。

滚动模糊时间窗算法的流程如图2所示。

图2 滚动模糊时间窗算法的流程图

算法中关于每条滑行道的使用时间为任意一个时间段内每条滑行道只允许一架航空器通过，且将由每条滑行道与之相关联的时间窗口来实现；此时间窗可以指定滑行道e作为路线一部分时的使用时间。一架航空器只会分配一条路线，这条路线包含一系列的时间窗，以确保航空器沿其滑行没有冲突。此外，为避免冲突，航空器间的最小间隔设置为60 m，以满足同一滑行道上连续航空器的分离。为确保滑行航空器的安全，在G上进行路线规划之前，找到每条滑行道e的冲突滑行道集Conf(e)，这些滑行道都是与e共用一个顶点或者在滑行道e60 m的范围内通过。当一架航空器在滑行道e上时，滑行道e的冲突滑行道集Conf(e)的时间窗就会更新，以防止其他航空器与之冲突。

3 算法应用实例

根据某机场飞行计划，随机选择航班，通过复制航班轨迹，获得不同流量水平的滑行数据。复制的航班虽使用原来的跑道，但进入跑道时间存在2 min的偏移。此外，通过这种方式，分别创建了95%、100%、110%、115%、120%和125%倍于原始飞机(725架)架次的集合，从而得到了从低密度交通流(低密度95%)，到实际运营交通流(中密度100%)，再到高密度的交通流(高密度125%)的运行场景。

在不同交通流密度下，分别采用BREEON’S法[14]和滚动模糊时间窗算法进行路径规划，以研究不同机位的滑行时间及平均滑行时间变化。并基于不确定度为1，统计分析在低、中和高3种交通流密度下的航空器滑行冲突次数和等待时间结果。

3.1 滑行时间

在这3种交通流场景中，通过设置不同的不确定度，即不确定度分别为0.2、0.4、0.6和0.8，分别采用BREEON’S法和滚动模糊窗口法进行路径规划，进而比较每个机位的进港滑行时间、离港滑行时间和总滑行时间，以及三者的变化情况与趋势。

图3～图5为低密度95%、中密度100%和高密度125%的实验场景下，基于不同不确定度分别采用BREEON’S法和滚动模糊窗口法时，各机位的平均滑行时间结果。其中，BREEON’SA表示BREEON’S法进港；RFTWA表示滚动模糊窗法进港；BREEON’SD表示BREEON’S法离港；RFTWD表示滚动模糊窗法离港；BREEON’S表示BREEON’S法进离港；RFTW表示滚动模糊窗法进离港。由图3～图5可知，航空器流量的增加导致各机位进港滑行时间、离港滑行时间和总滑行时间增加。其中，在相同的不确定度下，基于BREEON’S法各机位的进港滑行时间、离港滑行时间和总滑行时间均高于滚动模糊窗口法，平均高出2～3 min；在不同的不确定度下，滑行时间结果的变化趋势一致，结果证明滚动模糊窗口法对路径优化的有效性。

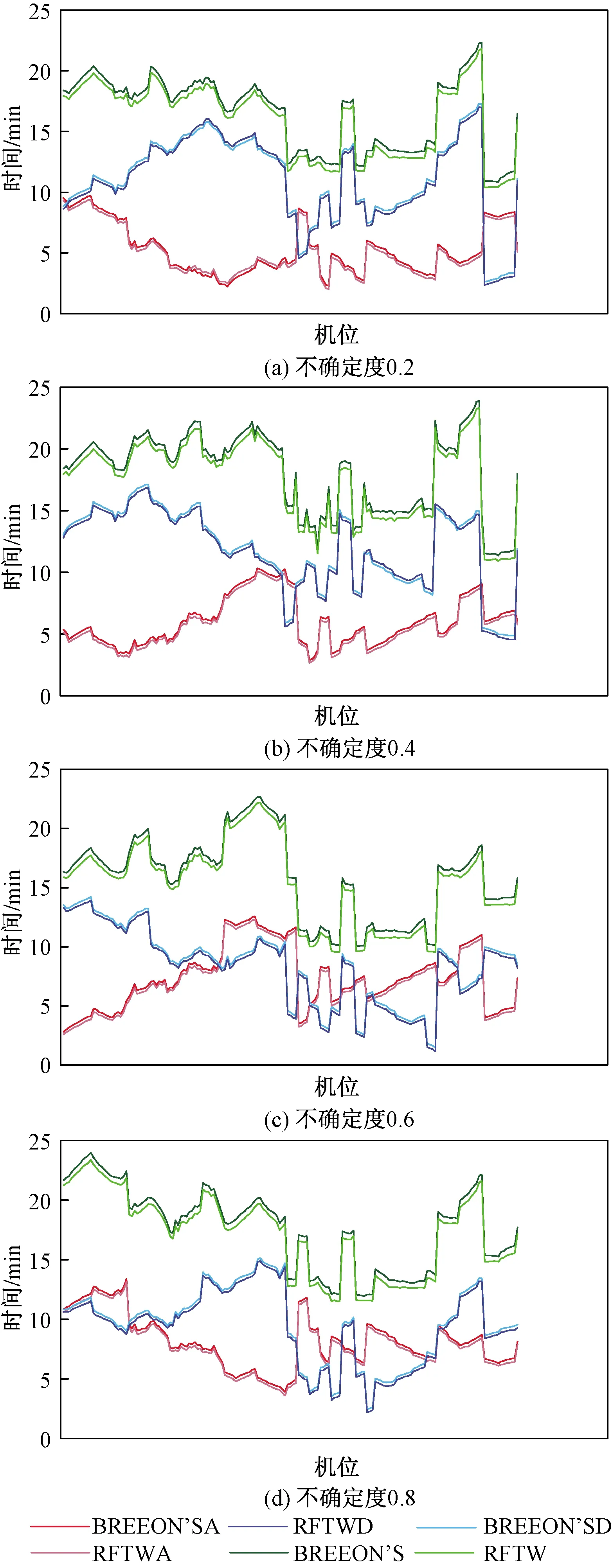
图3 低密度95%不同机位滑行时间图

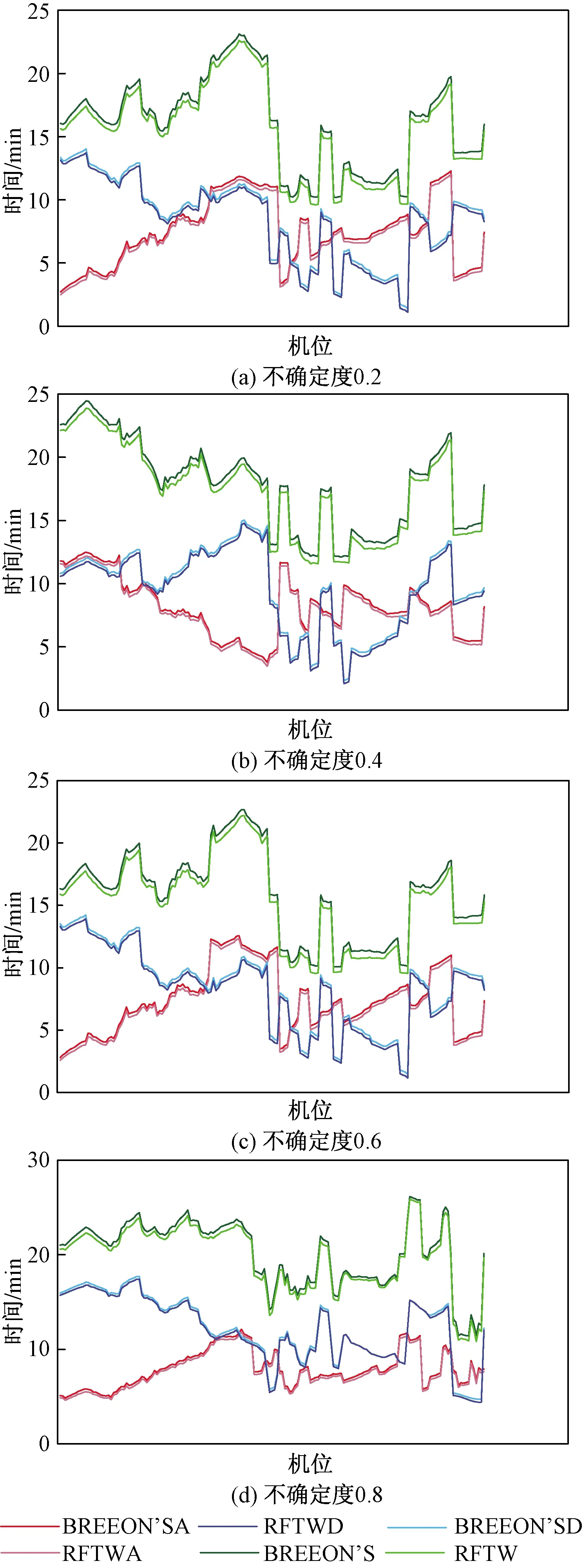
图4 中密度100%不同机位滑行时间图

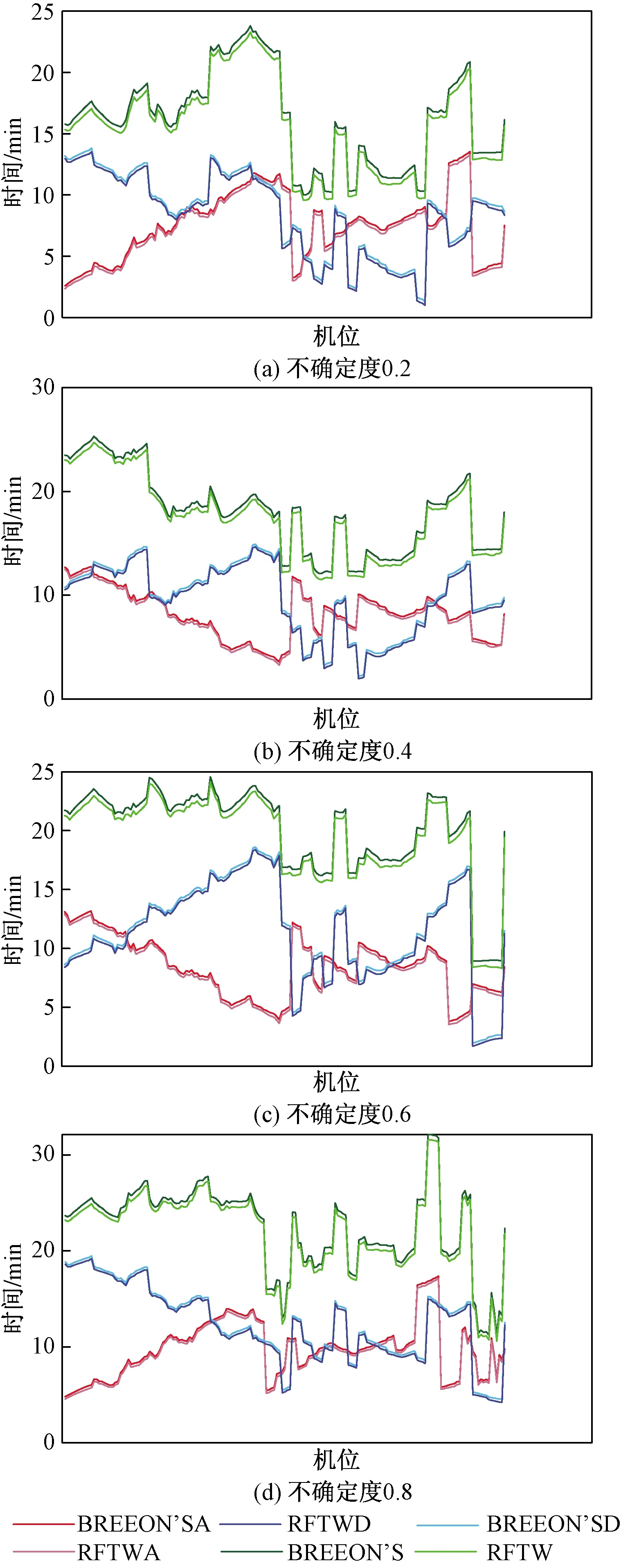
图5 高密度125%不同机位滑行时间图

此外，在这3种交通流场景中分别采用BREEON’S法和滚动模糊窗口法进行路径优化时，对比分析基于0.2、0.4、0.6和0.8的不确定度中不同机位的平均滑行时间，结果如图6所示。

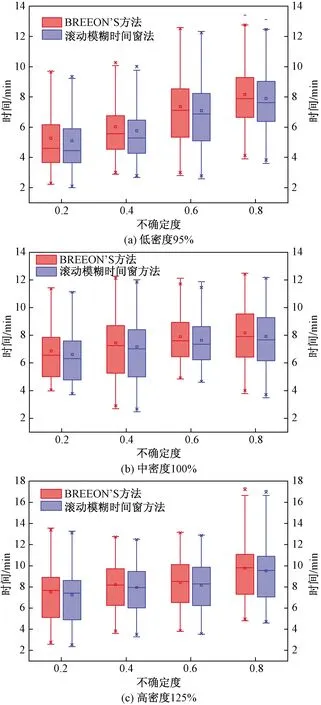
图6 3种密度交通流下不同机位平均滑行时间图

在低密度场景使用BREEON’S方法时，不同机位平均滑行时间的中位数随着不确定度的增大而继续增加。当不确定度为0.2时不同机位平均滑行时间中位数为4.5 min，不确定度为0.4时为5.1 min，不确定度为0.6时为7.2 min，不确定度为0.8时为7.5 min；且不同机位平均滑行时间的变化区间范围较大，平均滑行时间最大值与最小值之间的时间跨度较广。基于滚动模糊时间窗法时，不确定度的增加导致不同机位平均滑行时间的中位数亦增加；此外，不同不确定度下的中位数略高于BREEON’S法，但不同机位平均滑行时间的变化区间范围小于BREEON’S法，而且平均滑行时间的最大值和最小值之间的时间跨度也小于它。原因是低密度流量下，场面航空器的滑行顺畅，故两种方法的滑行时间结果相差甚微。

随着航空器流量的增加，不同机位的平均滑行时间相应增加。滚动模糊时间窗法通过提前排序，减少了航空器在场内滑行过程中停车的等待时间，进而可以相对减少平均滑行时间。通过图6(b)和图6(c)可知，滚动模糊时间窗法随航空器流量增长而平均路径优化效果提升。

3.2 滑行冲突

针对场面航空器滑行的拥堵问题，基于不确定度为1且在低、中和高3种交通流场景下，研究使用BROWNLEE’S法和滚动模糊时间窗口法优化航空器拥堵时的路径，以及统计分析滑行中所发生的冲突次数和滑行中的等待时间。具体数据结果如表2所示。

依据表2中的数据进行分析可知，冲突次数和等待时间随航空器流量密度的增加而增加。当采用BREEON’S法时，在航空器冲突次数方面，中密度比低密度增加187次，高密度比中密度增加189次；在航空器等待时间方面，中密度比低密度增长1.27倍，高密度比中密度增长1.25倍。采用滚动模糊窗口法时，在航空器冲突次数方面，中密度比低密度增加138次，高密度比中密度增加139次；在航空器等待时间方面，中密度比低密度增长1.18倍，高密度比中密度增长1.23倍。数据分析表明，采用滚动模糊窗口法进行路径优化，一定程度上减少了航空器滑行中的冲突次数和等待时间，从而提高了全场航空器滑行的效率。

表2 航空器滑行的冲突次数和等待时间

为更深入研究滚动模糊时间窗法在繁忙场景中的应用效果，用725架航空器为基数以依次增加0.5倍的航空器数量的方式，形成以762、798、834、870和907架航空器为基数的5种运行场景方案。基于滚动模糊时间窗算法进行路径优化，且分析此5种方案在不同不确定度下，航空器的日高峰小时架次、全天平均延误时间和高峰小时延误时间数据结果。数据结果如表3所示。

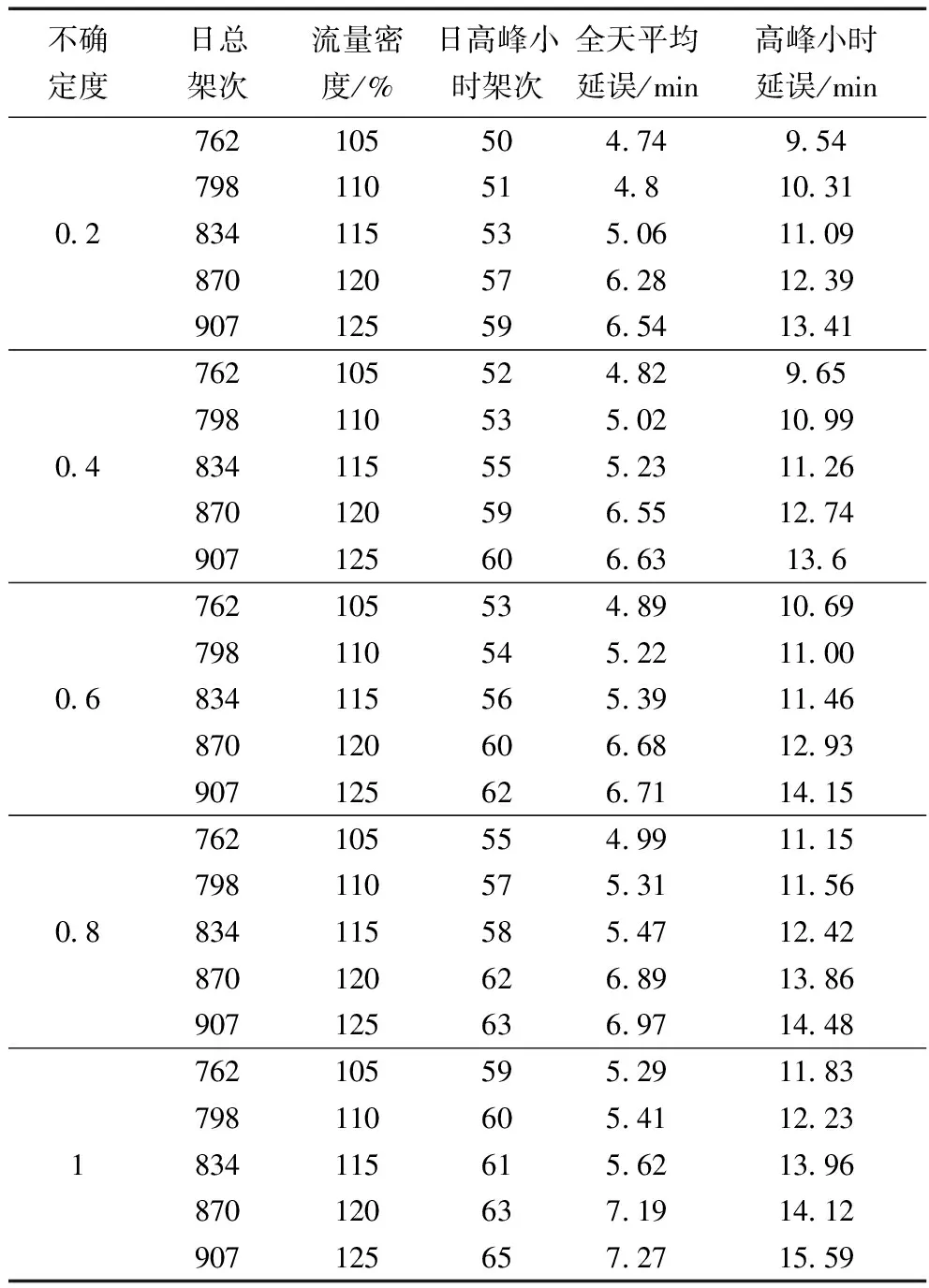
表3 基于滚动模糊时间窗算法的繁忙场景滑行数据

在不确定度相同的情况下，随着航空器密度的增加，航空器的平均全天延误和日高峰小时延误逐渐增加。但增长趋势缓慢，大部分平均全天延误增长不超过1.3倍。大部分日高峰小时延误增长不超过1.1倍。航空器的日高峰小时架次无明显变化。

随着不确定度的增加，同数量航空器架次场景下，航空器的平均全天延误和日高峰小时延误也随着不确定度的增加而增加。数据结果表明，随着场内航空器数量的增加和不确定度的增大，场内航空器滑行延误会有一定程度的增加，但增加幅度较小。证明采用滚动模糊时间窗法进行路径优化时，对场内航空器的延误时间的减少和繁忙机场运行效率的提高是有效的。

4 结论

机场场面航空器动态滑行路径优化是个非常复杂的问题，除了滑行路径间的冲突，还存在航空器进场和离场时间的不确定性以及跑道时间的不确定性。基于滚动模糊时间窗的动态滑行路径优化算法，对路径规划中存在路径冲突航空器的路线进行动态调整。选用某机场为例，对该算法进行验证，并与BREEON’S法进行对比，结果表明滚动模糊时间窗可减少航空器的滑行冲突，缩短滑行时间，降低滑行运行风险并提高机场的运行效率。