顶管电缆隧道施工对邻近建筑物和地下管线的扰动影响
2021-08-20马险峰曹明洋
马险峰,陈 飞,吴 冰,胡 超,曹明洋
(1.同济大学地下建筑与工程系,上海 200092;2.同济大学岩土及地下工程教育部重点实验室,上海 200092;3.喀什大学土木工程学院,喀什 844006;4.国网浙江省电力有限公司经济技术研究院,杭州 310007)
随着中国城市化进程不断加快,土地资源变得极为稀缺。大直径顶管电缆隧道作为城市输供电网的重要配套设施,不仅能显著提高电缆线路的输送能力,而且有利于城市土地资源的充分利用,已经被广泛地应用于中国的城市电网建设中[1-3]。电缆隧道的建设往往需要穿越密集的建筑物群和既有的城市地下管线,而电缆顶管隧道作为浅埋基础设施[4],易对邻近的建筑物和既有地下管线造成扰动。因此,顶管电缆隧道施工时尤其需要考虑其对邻近浅基础建筑物和地下管线的扰动影响。目前,中外许多研究学者通过有限元数值计算、物理模型试验和现场实测等方法探究了顶管隧道施工对邻近的建筑物和既有地下管线造成的扰动影响规律,并发表了相应的科研成果[5-8]。杨金虎等[9]采用数值模拟方法,研究了双层顶管隧道施工对土体竖向变形的影响规律,研究表明顶管隧道开挖引起的土体沉降主要是由于地层损失引起的。李明宇等[10]通过对某双线矩形顶管隧道的现场实测,研究了双线顶管隧道施工过程中地面沉降变化规律和分布特征。韩煊等[11]通过机理研究和实测数据提出隧道施工过程中预测建筑物沉降曲线的方法。但是,以上研究关于采用土工离心机试验探究顶管隧道施工对邻近浅基础建筑物和地下管线的扰动影响还不多见,而且现有关于隧道施工过程中预测建筑物沉降曲线的方法也没有考虑土体内摩擦角的影响。基于此,现以上海地区软黏土为例,采用离心机模型试验和有限元数值方法开展不同地层损失率工况下顶管电缆隧道施工对浅基础建筑物及地下管线的影响研究,并提出用于评估顶管施工对邻近浅基础建筑物扰动影响的修正Peck公式。研究成果将为顶管电缆隧道的建设提供一定的参考依据。
1 离心模型试验
相关研究表明地层损失是隧道开挖引起地层变形的主要原因[12]。采用离心机试验模型试验,探究不同地层损失率下顶管电缆隧道施工对邻近浅基础建筑物和地下管线的扰动影响规律。
1.1 试验工况
试验在同济大学的TLJ-150复合型岩土离心试验机上开展。工程中顶管施工产生的平均地层损失率在1%~3%范围内[13],因此,分别设置地层损失率为1%、2%和3%的3个工况来进行离心机模拟。采用排液法模拟不同地层损失率的工况,测定不同地层损失率下顶管电缆隧道施工时地表沉降、邻近普通砖混建筑物和铸铁管线及混凝土管线的沉降变形,分析顶管隧道施工对邻近建筑物和地下管线扰动影响。地表沉降和建筑物沉降采用激光位移计测量,管线变形采用应变片测量然后积分得到。
1.2 模型设计和制作
模型箱的尺寸为500 mm(宽)×800 mm(长)×500 mm(高),试验模型布置图及构件详图如图1所示。
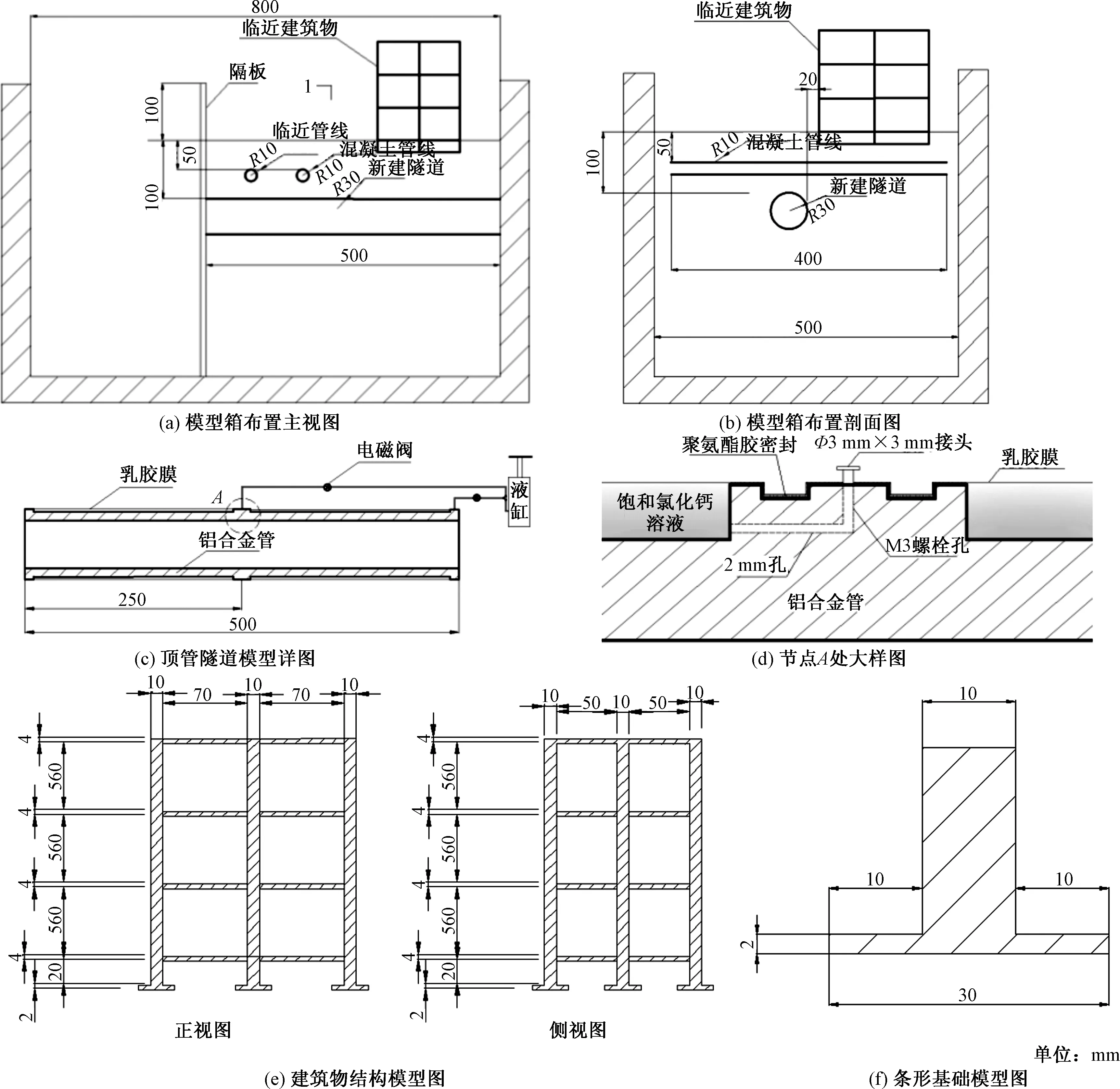
图1 试验模型布置图及构件详图
1.3 隧道、建筑物和管线模型设计
采用铝合金空心管模拟隧道结构,试验中相似比N=50,根据等效刚度原理[14][式(1)],可得出试验结构材料参数如表1所示。
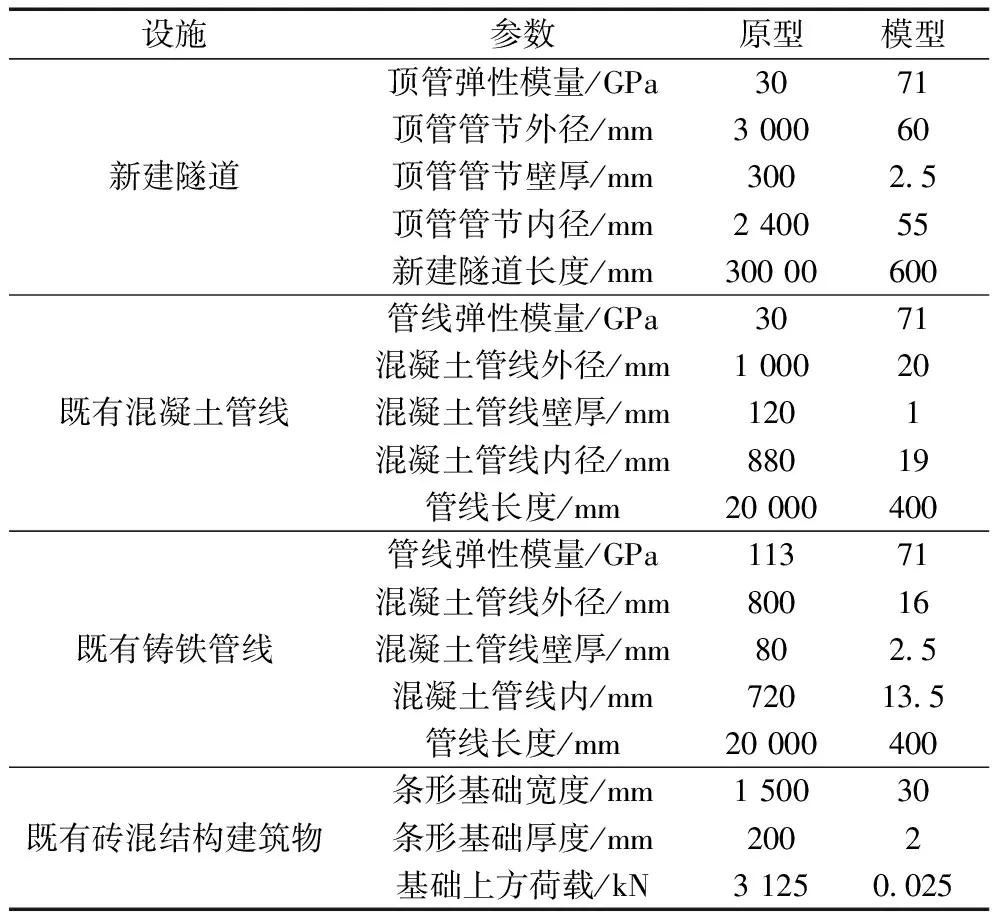
表1 模型参数表
(1)
式(1)中:Em、Ep分别为模型和原型的弹性模量;νm、νp分别为模型和原型的泊松比;tm、tp分别为模型和原型的厚度;N为相似比,N=50。原型基础的Ep=25 GPa,tp=200 mm,νp=0.2;基础模型的Em=207 GPa,νm=0.29,计算得到铝板基础模型厚度tm=1.95 mm,此处取2 mm。
1.4 实验步骤
为了保证在离心机中固结时隧道周围溶液延长度方向能均匀分布,将乳胶套延隧道长度方向均分为两段,每段长为220 mm。已知顶管管节模型外径为60 mm,乳胶膜直径为70 mm,可得出1%、2%和3%这3个地层损失率对应的每个乳胶套需要累计排出液体量分别为8.5、17和15.5 mL。试验的详细步骤如下。
(1)模型箱填土,安装并固定好新建隧道后覆土固结。
(2)埋设地下管线和安装建筑物模型并固结。
(3)打开第一个乳胶膜电磁阀,启动电机,通过电机运动时间换算得排液8.5 mL时依次关闭电机和电磁阀。
(4)打开第二个乳胶膜电磁阀,启动电机,通过电机运动时间换算得排液8.5 mL时依次关闭电机和电磁阀。
(5)测定既有管线应变值和建筑物4个角点沉降值,固结一段时间后再测量,得出地层损失率为1%情况下顶管施工对邻近建筑物和既有管线的影响。
(6)重复以上步骤,得出地层损失率为2%和3%情况下顶管施工对邻近建筑物和既有管线的影响,试验模型图如图2所示。

图2 试验模型图(1∶10)
1.5 试验结果和结论
地表沉降由试验前后对应位置激光位移计示数差换算得到[图3(a)],建筑物不均匀沉降由靠近隧道面底板和远离隧道面底板激光位移计示数差换算得到[图3(b)]。通过对应变片原始数据进行整理分析,得到不同地层损失率条件下顶管隧道开挖对混凝土管、铸铁管的扰动影响规律,计算结果如图4(a)和图4(b)所示。
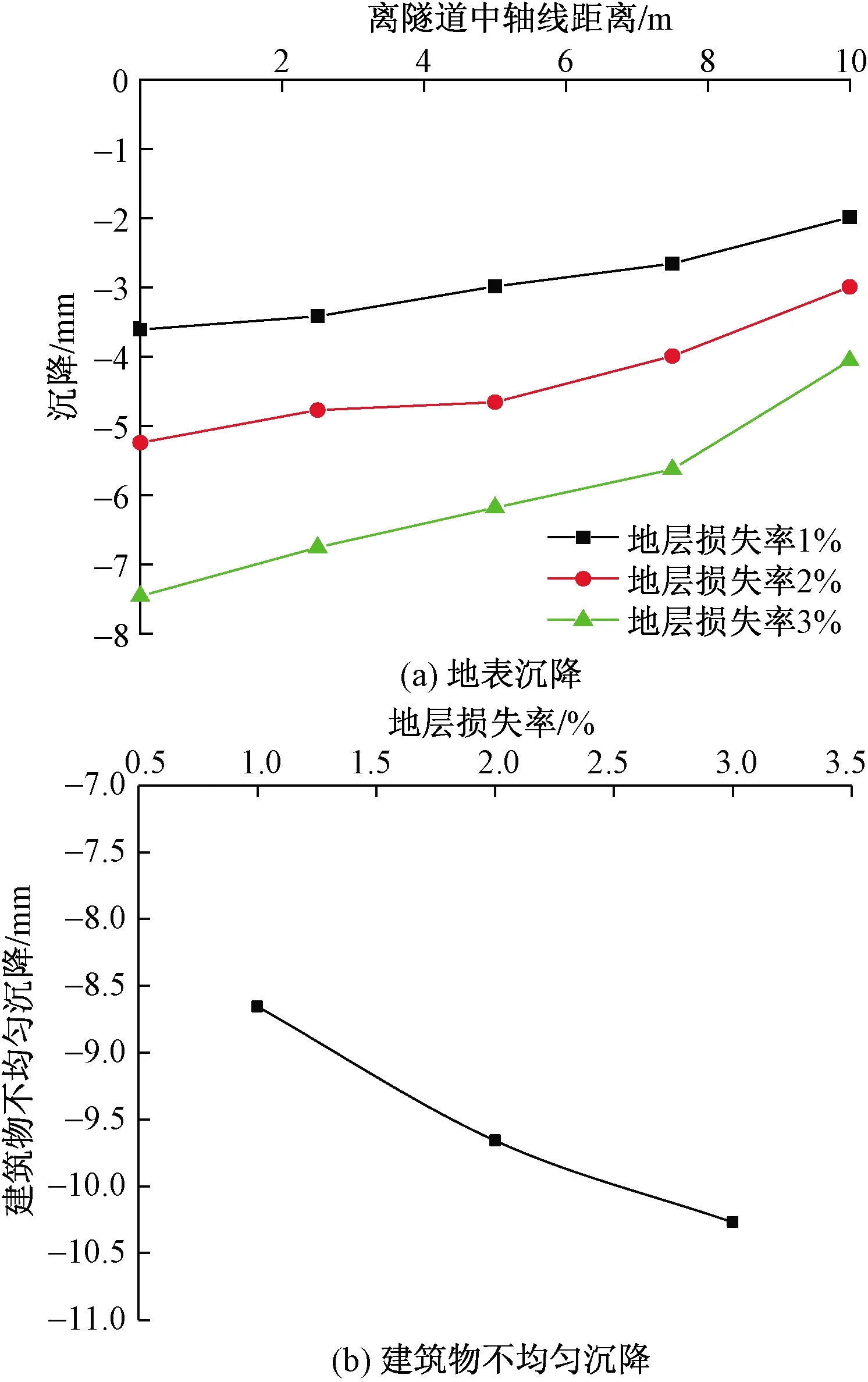
图3 不同地层损失率下的地表沉降和建筑物不均匀沉降
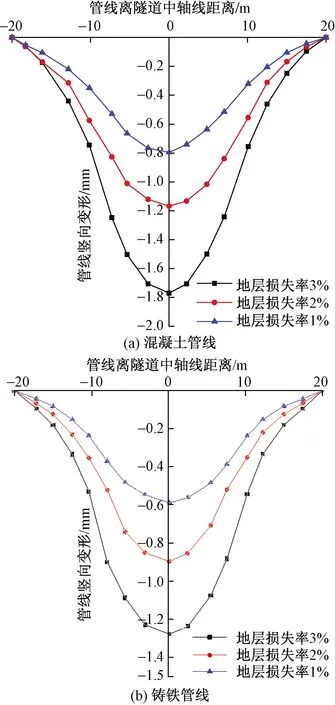
图4 不同地层损失率下混凝土管线和铸铁管线变形曲线
由试验结果可知:随着地层损失率的增大,地表沉降和建筑物沉降差显著增大,这与文献[15]中报道的现场测试结果一致;随着地层损失率的增大,铸铁管和混凝土管竖向变形均显著增大,但铸铁管的竖向变形小于混凝土管,这也说明了地下管线刚度的增加可以有效减小邻近顶管隧道施工的扰动影响。
2 有限元数值模拟
采用PLAXIS 3D2016有限元软件研究软黏土地层顶管电缆隧道施工过程中不同地层损失率对邻近浅基础建筑物及地下管线的扰动影响规律。
2.1 数值模型的建立与计算参数选取
为了模拟顶管电缆隧道施工对邻近建筑物和地下管线的扰动影响,分别建立顶管电缆隧道-土体-浅基础建筑物和顶管电缆隧道-土体-地下管线的共同作用模型,并在模拟中做出以下假设:①模型中的每层土体各向同性,且都遵循Drucker-Prager(D-P)准则;②不考虑顶管机头和管道连接处的影响,认为管道的材料为各向同性的线弹性体;③正面顶推力的加载面与工具管的切削面大小相同,并且顶推力均匀分布在这个圆面上;④在顶管施工模拟过程中不考虑土体变形的时间效应,仅仅考虑顶进空间距离上的变化;⑤不考虑施工前土体自重应力产生的变形;⑥地下管线与土体始终保持接触,不发生相对滑动。
模型中土体的几何宽度和深度为分别取80 m(X向)和40 m(Y向)以减小边界效应对模拟计算的影响。土体模型的顶面为自由面无约束,底部施加完全固定约束,两侧竖直边界施加滑动约束(Ux=0,Uy自由)。本次数值模拟拟采用小应变硬化土模型(hardening soil model with small strain stiffness,HSS)来模拟土体的变形特性,建筑物、顶管电缆隧道和地下管线采用线弹性本构模型。本次数值模拟采用上海交通大学测定的上海地区软黏土参数,如表2、表3所示。电缆顶管隧道、建筑物和地下管线的计算参数分别如表4~表6所示。
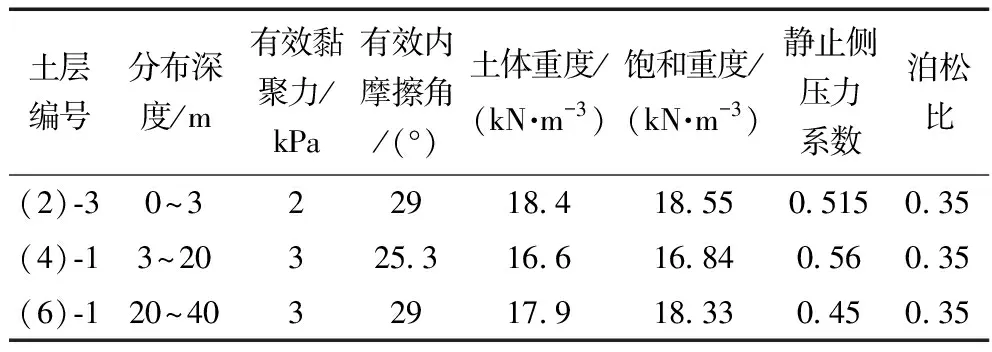
表2 土层参数

表3 土层参数

表4 建筑物参数
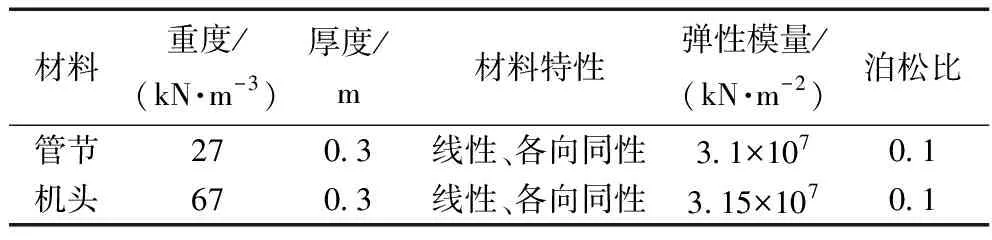
表5 顶管电缆隧道参数

表6 地下管线参数
2.2 数值模拟工况和结果分析
数值模拟工况:顶管电缆隧道模型的直径为3 m,埋深为5 m,管节为3 m,总顶进距离为33 m,管道周围摩阻力取3 kPa,机头压力和注浆压力都取管道中心处静止土压力119.6 kPa。分别取地层损失率为1%、1.5%、2%、2.5%和3%共5个工况下顶管电缆隧道开挖对邻近浅基础建筑物和地下管线的影响规律开展数值模拟研究。数值计算得到曲线如图5所示,数值计算结果表明:在地层损失率为1%~3%范围内,随着地层损失率增加,建筑物不均匀沉降和管线竖向位移最大值皆逐渐增大,且数值模拟的计算结果与前述的离心机试验结果趋势一致。
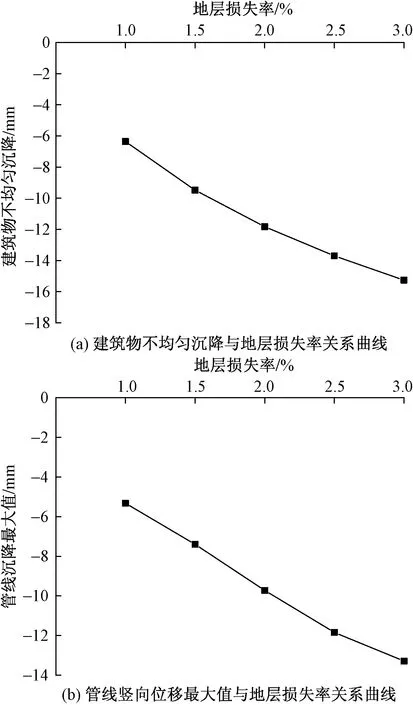
图5 数值模拟曲线
2.3 Peck公式的修正
韩煊等[11]提出一个考虑建筑物结构刚度的建筑物沉降曲线的预测方法,计算公式为
(2)
式(2)中:
(3)
KS=βMβdβgβHK
(4)
βM=0.70M0.2
(5)
(6)
(7)
式中:s(x)为采用修正公式得到的地面任一点的沉降值,m;AL为隧道截面积,m2;VS为修正的地层损失率(考虑隧道和建筑物的夹角为α时);KS为修正沉降槽宽度参数;z0为隧道轴线埋深,m;x为距隧道轴线的横向水平距离,m;V为地层损失率;βM为建筑物剪切刚度修正系数;M为建筑物截面剪切刚度,109N;G为梁板柱等建筑物构件的剪切模量,N/m2;ζ为建筑物有门窗洞口时的刚度折减系数;A为对应建筑物构件的截面积,m2;βd为考虑基础埋深的沉降槽宽度参数修正系数;h为基础埋深,m;βg为建筑物自重对建筑物沉降的沉降槽宽度参数修正系数,取βg=1;βH为考虑建筑物与隧道轴线之间距离的沉降槽宽度参数修正系数,取βH=1;K为沉降槽宽度参数;φ为土的有效内摩擦角。
对于Peck曲线中沉降槽宽度系数K的取值,目前应用最多的O’reilly等[16]提出的经验取值法(即根据不同的土质直接赋予其经验值,一般规定软黏土取0.7)。由于软黏土有效内摩擦角并不是一个固定值,不同地区、成因的软黏土的有效内摩擦角会有差异。对工况相同但所在土层有效内摩擦角不同的顶管电缆隧道开挖进行了数值模拟分析,得到了对应的地表沉降曲线,将从这些地表沉降曲线中分析得出的沉降槽宽度系数值进行研究,拟合得出了其与土体有效内摩擦角的对应公式。利用Origin2019软件进行曲线拟合,根据散点图规律假设拟合函数形式为
y=Ae-x/t+y0
(8)
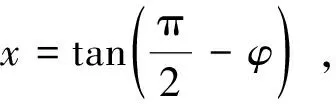
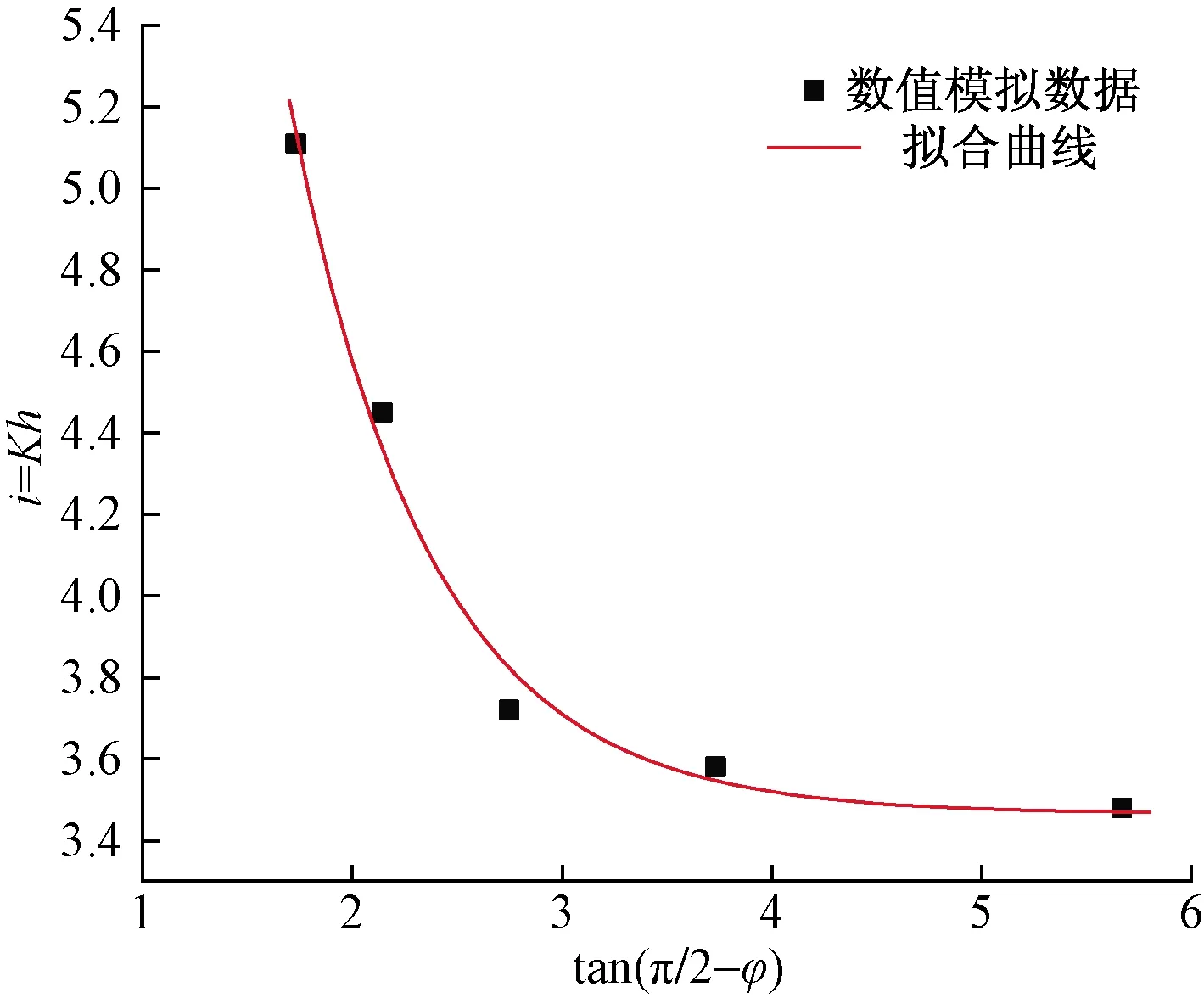
图6 沉降槽宽度系数与土体有效内摩擦角关系
通过处理,得到A=22.98,t=0.66,y0=3.466,因此得到软黏土沉降槽宽度系数K与其有效内摩擦角的对应关系为
(9)
由于该修正公式是基于数值计算结果总结提出的,为了证明该修正公式的正确性,将该公式应用于杭州萧山燃机顶管项目[顶进距离为600 m(沉降已相对稳定)时11号监测点]地表沉降预测(即将建筑物刚度修正系数取1用于预测地表沉降),将该修正公式预测的地表沉降曲线与现场监测数据及未修正的Peck沉降曲线进行对比,结果如图7所示。
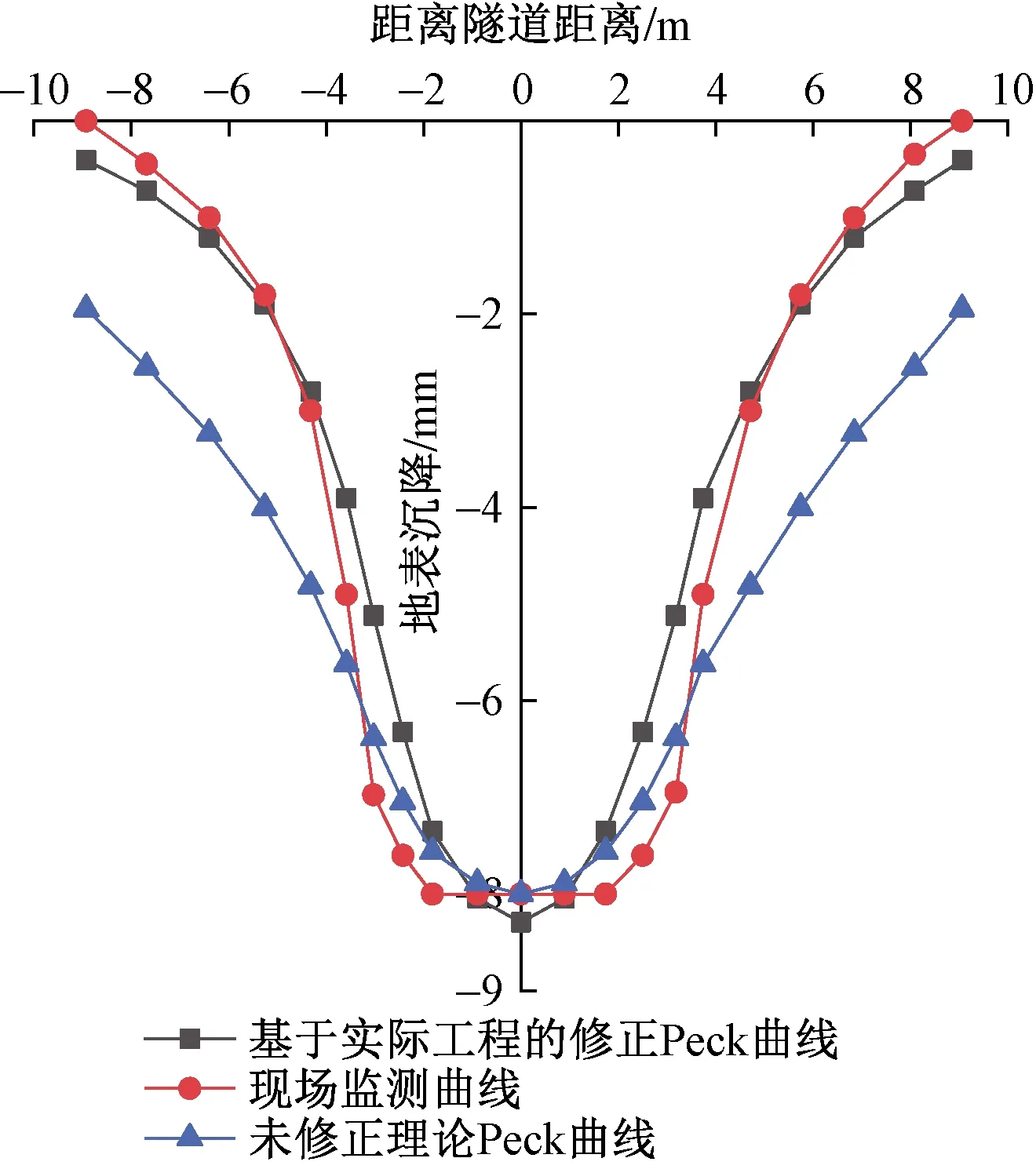
图7 未修正及修正后的Peck沉降曲线与现场监测数据对比图
如图10所示,修正后的Peck计算公式能更好地符合现场监测数据规律,说明提出软黏土范围内对经典Peck曲线的修正方法能更好地反映顶管电缆隧道开挖对周围地层产生的扰动影响。
3 结论
通过离心机试验和有限元数值计算方法探究了软黏土地区顶管电缆隧道施工对邻近建筑物和地下管线的扰动影响,得出以下结论。
(1)顶管电缆隧道施工时,随着地层损失率的增大,邻近浅基础建筑物不均匀沉降和地下管线竖向位移皆增大,且大刚度的地下管线相较于小刚度的地下管线扰动影响更小。
(2)有限元数值模拟方法可以较好地模拟顶管隧道在不同地层损失率的工况。
(3)提出的修正Peck公式可以较好地评估在软黏土区域的顶管电缆隧道开挖对周围地层产生的扰动影响。
