地下水渗流对单U形地埋管埋深的影响
2021-08-20李泽锟杜震宇
李泽锟,杜震宇
(太原理工大学土木工程学院,太原 030024)
随着世界能耗增加和环境问题的加剧,可再生能源受到越来越多的关注。土壤源热泵由于其具有充分利用地热、稳定性高、占地面积小的特点而被广泛应用。地埋管换热器是土壤源热泵的重要组成部分,其埋深和换热能力直接影响到整个系统的初投资和运行效率。地埋管换热器的换热受到较多因素的影响,其中最主要的是地埋管周围岩土体的热物性和地下水的分布。由于传统的均质换热模型并未考虑埋管周围岩土体轴向分层和地下水的影响,与实际情况存在较大的误差。为了使模拟更加准确,中外很多学者针对岩土体分层和地下水渗流进行了一系列的研究。
在岩土体分层方面,王泽生等[1]建立了岩土体的轴向和周向的二维分层模型,但并未考虑地面与空气的换热和U形管末端的影响。黄雪婷[2]建立耦合地下水渗流和岩土热物性分层的全尺寸三维模型,研究地下水位线高度、渗流速度和岩土分层对地埋管换热的影响。Abdelaziz等[3]根据有限长线热源模型,得到地埋管周围岩土体任意一点处的温度响应,并根据各层的导热系数得出分层换热量。Chen等[4]建立三维分层模型,研究换热量随埋管深度的变化。李永等[5]通过实验的方法测得100 m深的岩土热物性,建立三维分层岩土数值模型,并将岩土初始温度的影响考虑在内。
在地下水渗流方面,李蕾等[6]根据岩土热物性测试的结果建立数值模型,对三种渗流速度下地埋管管群的出口温度进行模拟与分析,得到最佳钻孔数和最佳埋管深度。Li等[7]建立三维数值模型,通过热物性测试和ASHRAE方法将地下水作用下的岩土导热系数和比热容等效为无渗流的导热系数,同时研究了含水层厚度对热物性测试的影响。得出结论为地下水位线对热物性的影响较小,但是其越靠近地面,等效导热系数越大。张山等[8]通过FEFLOW数值模拟软件建立了三维瞬态传热模型,模拟分析了有无地下水渗流及不同渗流速度和含水层厚度下岩土温度场和换热量的情况。
从上述文献可以看出,中外学者的研究多是关于岩土体换热模型的优化和地下水对岩土温度场的影响,分层岩土和地下水共同作用下的地埋管最佳埋深与分层换热量的研究相对较少。现阶段工程中多采用经验公式来计算地埋管的埋深。由于计算方法的不准确,导致地埋管埋深过大,不但影响换热效率,而且经济性较差。所以亟待提出一种准确确定地埋管埋深的方法。李明洪等[9]提出通过分层地质结构指导埋深,但地下水对地埋管的埋深也有较大影响。地埋管在通过含水层时换热剧烈,导致含水层以下的埋管部分换热效果不佳。故在黄土高原地质条件的基础上,现综合考虑分层岩土体和地下水的作用,并将岩土原始温度考虑在内,通过ANSYS建立地埋管换热器及其周围岩土体的三维非稳态换热模型,对不同含水层厚度、地下水渗流速度和地下水位线高度进行模拟,从而得到该地区地埋管的最佳埋深和分层换热量。
1 模型的建立
1.1 模型的假设
地埋管换热过程是复杂的非稳态换热,为了简化计算,需要对模型进行简化。
(1)对计算区域的岩土体进行分层,在各层内将岩土视为均质介质,且岩土热物性不随时间和空间变化而变化。
(2)假设循环流体、埋管、回填材料和土壤之间不存在接触热阻。
(3)将含水层岩土的地下水渗流考虑在内,假设地下水渗流只沿水平方向存在且速度恒定。
(4)假设固体和液体在接触的瞬间达到热平衡状态。
(5)忽略埋管底部弯管的影响。
1.2 物理模型
以参考文献[10]中的实验为基础建立模型。假设计算区域为3 m×3 m×70 m的六面体岩土体,钻井为圆柱体设置在计算区域的几何中心。沿深度方向将岩土体分为5层,从上至下分别为湿陷性黄土、黄土、卵石、强风化砂岩和中风化砂岩。回填材料为砂土,U形管为聚乙烯(PE)管,循环流体为水。具体热物性参数如表1所示。
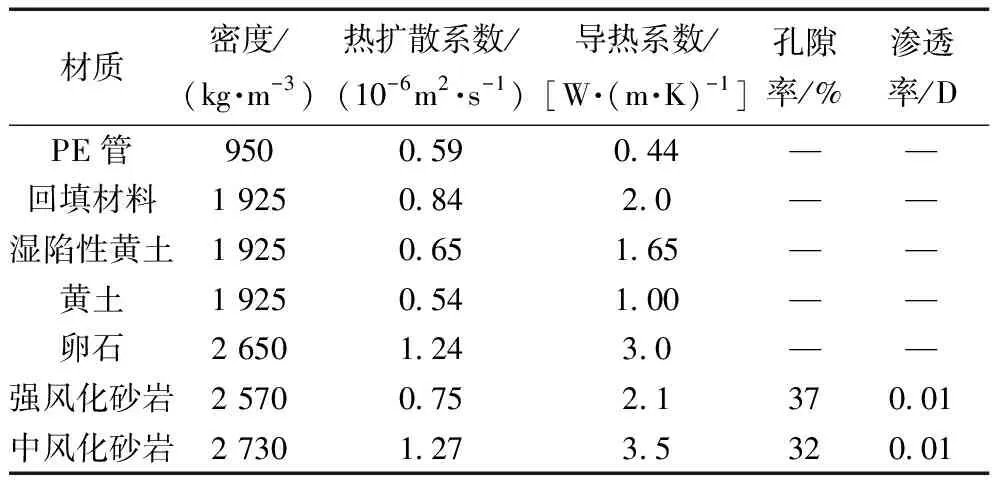
表1 热物性参数
通过ANSYS内的workbench建立分层岩土体的三维非稳态地埋管换热模型。通过Meshing对几何模型进行网格的划分,根据划分网格的原理,由于计算区域的温度变化沿深度方向相对水平方向较小,所以竖直方向的网格划分相对稀疏,对水平方向的网格进行加密处理。由于忽略底部弯管的影响,通过用户自定义函数(user-defined functions,UDF)将进水支管与回水支管的底部连接起来。
1.3 数学模型
1.3.1 多孔介质的控制方程
(1)连续性方程。
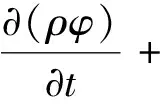
(1)
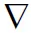
(2)动量方程。
(2)
由于假设多孔介质各向同性,所以可将源项简化为
(3)
式(3)中:Si为动量方程的源项;μ为动力黏度;u为水在水平方向的流速;a为渗透系数,取a=0.01;C2为惯性阻力系数,取C2=2.33。
(3)能量方程。
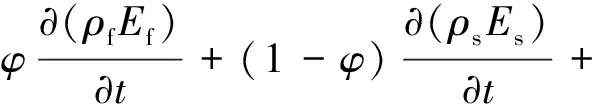
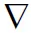
(4)
式(4)中:Ef、Es分别为液体的总能和固体的总能;aeff为有效热扩散率,aeff=φaf+(1-φ)as,其中af、as分别为液体、固体的渗透系数。
1.3.2 数值计算方法
采用Realizablek-ε双方程湍流模型,通过基于算子分裂的压力隐式算法(pressure implicit with splitting of operators,PISO)对状态方程进行求解。离散格式为二阶迎风格式。进行非稳态计算时,时间步长设置为60 s,收敛条件除能量残差设置为10-8,其余残差设置为10-6。
1.4 定解条件
1.4.1 初始条件
将岩土体设置为多孔介质,岩土体周围的边界设置为恒温边界,温度值与岩土体初始温度相同。根据参考文献[11]可知,在进行地埋管换热器的模拟计算时,岩土的初始温度对结果影响较大,所以根据试验测量的岩土初始温度场t0沿深度z方向变化的公式为
(5)
1.4.2 边界条件
忽略太阳辐射的影响,将计算区域顶部设置为第三类边界条件,其中流体温度设定为夏季典型日随时间变化的空气温度,具体公式为
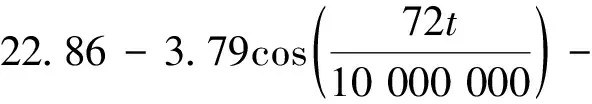
(6)
式(6)中:Tup为外界空气温度,℃;t为时间,s。
地面与周围空气的对流换热系数为0.48 W/(m·K)。在含水层设置一定流速的地下水渗流,地下水温度与岩土体初始温度相同。U形管的入口设置为速度入口,入口温度随夏季典型日逐时冷负荷的变化而变化,出口设置为压力出口。具体的入口温度随时间变化如图1所示。
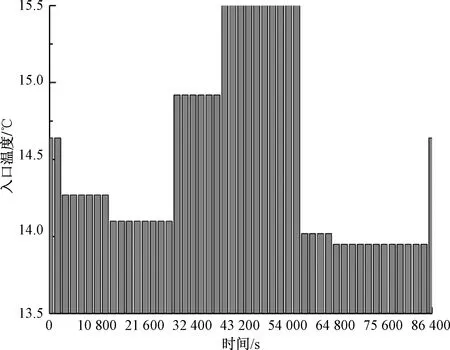
图1 入口温度随时间变化
1.5 网格独立性检验
作为数值解的网格应该足够细密,以至于在进一步加密网格对数值解已经几乎没有影响。这种数值解称为网格独立的解[12]。为获得网格独立的解,对于网格数量分别为222 327、497 608、791 652、1 062 233、1 267 854的模型进行模拟,设置进口温度为15 ℃,进口流速为0.23 m/s。待岩土温度场达到稳定之后,得到回水侧循环流体沿深度方向的温度分布,结果如图2所示。
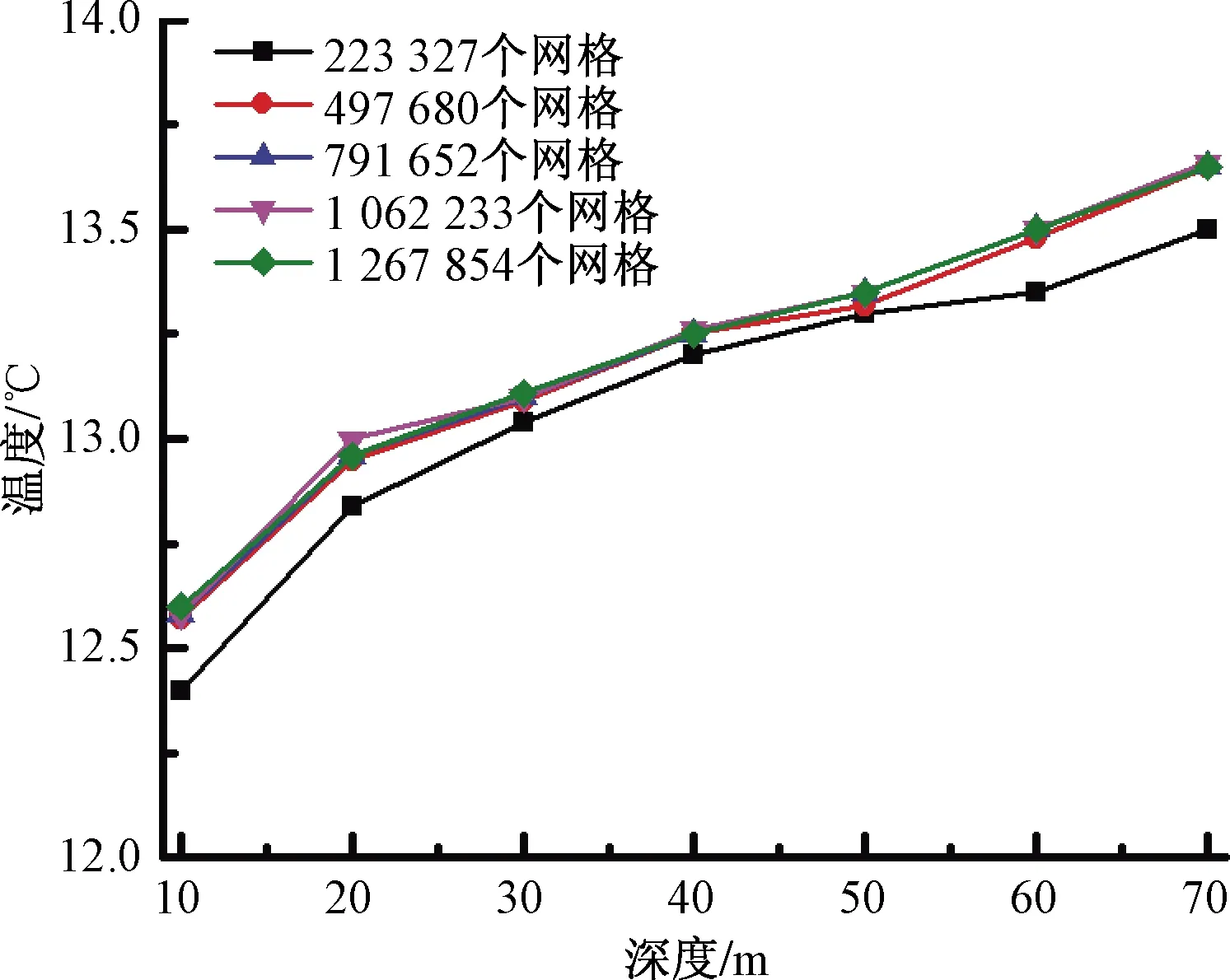
图2 网格独立性检验
对于网格数量为497 680的模型,回水侧水温沿深度方向分布差距较小。综合考虑计算耗时和模型的精确度,选择497 680个网格的模型。
2 模拟与结果分析
2.1 评价指标
单位井深换热量是衡量地埋管换热器换热能力的参数,其表达式为
(7)
根据参考文献[9],分层单位井深换热量可以直观地反映每个岩土层换热能力,其表达式为
qi=cm[(Tin,i-Tout,i)-(Tin,i+1-Tout,i+1)]/hi
(8)
式(8)中:qi为第i层岩土体的单位井深换热量,W/m;Tin,i和Tout,i分别为第i层岩土体顶面进水温度和出水温度,℃;hi为第i层岩土体的厚度,m。
为了更加简单有效地观察各层岩土体的换热量占总换热量的份额,进而确定最优的埋管深度,提出分层单位井深换热比率,表达式为
(9)
式(9)中:Ni为第i层的分层单位井深换热比率;当Ni<1时,此岩土层为低效换热;当Ni<0时,此岩土层为无效换热。
2.2 模型的验证
通过与试验对比的方式来证明模型的准确性。选取参考文献[10]中2011年7月24日在不同深度的供回水侧温度测量数据与模拟结果进行对比。
如表2所示:数值模拟得出的结果与实验结吻合良好,两者之间的相对误差不超过3%,误差产生的原因可能是实验中的埋管是以管群形式存在,各埋管相互之间有一定的干扰。误差相对较小且在允许范围内,因此数值模型是准确的。

表2 夏季制冷工况模拟值与实验值对比
2.3 地下水对最佳埋深的影响
降低地埋管换热性能的负面传热过程称为热回流[10]。热回流主要来自两个方面:①地埋管在某一层岩土体内换热剧烈,导致该层以下的岩土体对换热有负面作用;②供回水支管间的热短路。由于岩土体分层和地下水渗流的存在,管内水通过不同岩土层或含水层时,水温沿深度方向不止一次出现极大值和极小值,即多次出现热回流现象,造成了埋管后半部分为无效换热,同时也影响了整个系统的换热效率。为解决这一问题,以夏季典型日为例,在岩土原始温度和热物性参数已经确定的情况下,分析不同的地下水条件对地埋管最佳埋深的影响。
2.3.1 含水层厚度对最佳埋深的影响
假设渗流速度为1×10-5m/s,含水层厚度为10 m(埋深27.6~37.6 m),连续运行96 h,在72 h后出口温度趋于稳定。水温和分层单位井深换热比率沿深度方向的变化如图3所示。
在整个换热过程中,供水支管内水温并非沿深度方向线性下降。在埋深38 m左右,温度达到最低值13.6 ℃,随着深度的增加,水温逐渐上升,最高达到了14.4 ℃。这可能因为地埋管在含水层区域换热剧烈,导致供水侧水温在38 m后低于岩土温度,岩土对水起到加热的作用。在55 m左右温度再次下降,这可能是因为岩土的温度相对较低,对支管内的水进行了再一次的降温。在回水支管中,水温随高度增加呈下降趋势。在38~48 m处回水侧温度高于供水侧。这是因为地下水对岩土温度场的干扰使得热量在渗流速度方向下游出现堆积,导致回水侧的岩土体温度高于供水侧。由于地下水的作用,回水侧水温在含水层区域出现明显下降,在11.5 m处达到最低的13.2 ℃。由于在出口附近供水支管与回水支管有较大的温差,出口处的水温受到支管间热干扰出现了升温,最终出口温度为13.3 ℃。
通过分层单位井深换热比率对整个支管沿程换热能力进行分析,由于前两层岩土体导热系数较小,其所占总换热量的比率相对较小,Ni分别为0.48和1.03。在27.6~37.6 m处,地下水对换热的强化作用使得Ni在31 m处达到最高值,为4.47。随后Ni值便急剧下降,在45~59 m处,Ni<0,即岩土体对埋管的换热起到了负面作用。0~37.6 m的换热量占总换热量的92.4%,其中含水层换热量为72.3%。可以看出,在地下水作用下,地埋管多次出现热回流现象。综合水温和Ni沿深度方向的变化,可以得出含水层以下的埋管换热都为低效或无效换热。此时地埋管的最佳埋深为38 m。
当含水层厚度为20 m(埋深27.6~47.6 m)时,水温沿深度变化如图4所示。水温的变化趋势与图3相同,但由于含水层厚度的增加,地下水对埋管换热作用的距离变长。相比较10 m含水层厚度的情况,整个埋管换热量增加了24.5%。热回流出现在47~55 m处。47.6 m之前的换热量占总换热量的96.2%。同时,Ni在47 m处已经小于1,从而证明埋管同样在含水层以下为无效换热。此时地埋管的最佳埋深为47 m。

图3 含水层厚度为10 m的水温和Ni
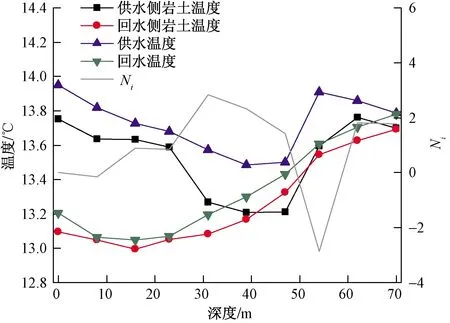
图4 含水层厚度为20 m的水温和Ni
当含水层厚度为30 m(埋深27.6~57.6 m)时,总换热量相比20 m含水层厚度提高了32.3%。如图5所示,水温在含水层处出现明显的下降,在46 m左右达到最低温度13.1 ℃。在46~51 m区域内,虽然供水温度已出现热回流,但是由于回水温度还存在较大的温降,此区域内埋管换热仍为有效换热。Ni在51 m下降为0,埋管在51~66 m处为无效换热。此时地埋管的最佳埋深为51 m。
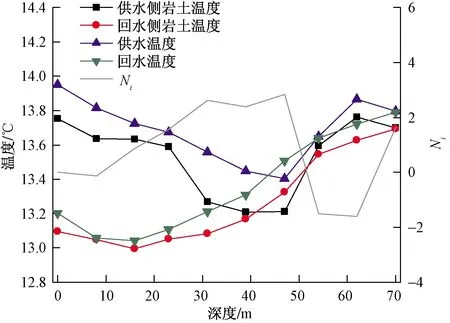
图5 含水层厚度为30 m的水温和Ni
对含水层厚度分别为30 m(埋深27.6~57.6 m)、35 m(埋深27.6~62.6 m)、40 m(埋深27.6~67.6 m)、42.4 m(埋深27.6~70 m)的模型进行模拟,如6图所示,随着含水层厚度的增加,Ni的波动幅度变缓,这是因为在渗流速度相对较大的情况下,含水层厚度的增加对换热量起到促进作用,地埋管换热器的总换热量随着含水层厚度的增大而增大,导致不含地下水的上层岩土体换热量占总换热量的份额减小。但出现热回流的位置并未随含水层厚度的增大而变化,Ni仍在埋管深度为50~52 m的区域内下降为0。对比图3、图4、图5、图6可知,当含水层厚度较小时,循环流体经过含水层后便出现热回流的现象;当含水层厚度较大时,热回流出现的位置出现在含水层内部。
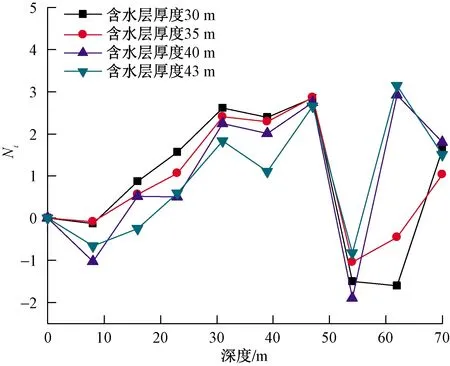
图6 不同含水层厚度下的Ni
因此存在典型含水层,当其厚度大于实际含水层厚度时,最佳地埋管埋深为实际含水层的底部;当典型含水层厚度小于实际含水层的厚度时,最佳埋深的位置在典型含水层的底部。通过以上的模拟结果可知,在黄土高原寒冷地区的地质条件下,地下水渗流速度为1×10-5m/s时,典型含水层厚度约为23 m。
在之前的研究中,为了防止温度传感器对管内流体的流动和换热产生影响,大多实验通过测量供回水外侧管壁的温度和支管的热阻来计算管内循环流体沿深度方向的温度变化[10]。但从供回水侧岩土体温度沿深度变化曲线可以看出,含水层的供水侧岩土体温度在地下水的作用下温升较小,回水侧由于热堆积而温度较高。供回水侧岩土体温度变化与水温变化趋势相近,但是水温变化整体滞后,所以通过地埋管的管壁侧温度推算出的最佳埋深比实际值偏小,相差大约为5 m。
典型含水层厚度可以有效地确定地埋管的最佳埋深,但其大小受到很多因素影响,其中主要影响因素是当地地质条件和地下水情况。对于黄土高原地区,各层岩土体的热物性与表1基本相同,差距较大的是含水层厚度、地下水渗流速度和地下水位线的高度。在确定含水层厚度的情况下,通过模拟研究渗流速度和地下水位线高度对典型含水层厚度的影响,进而得到地埋管的最佳埋深。
2.3.2 地下水渗流速度对最佳埋深的影响
假设地下水位于埋深27.6~70 m的区域内,分别得出渗流速度为3×10-5、1×10-5、5×10-6、3×10-6、1×10-6、5×10-7、3×10-7m/s情况下Ni的变化,如图7所示。
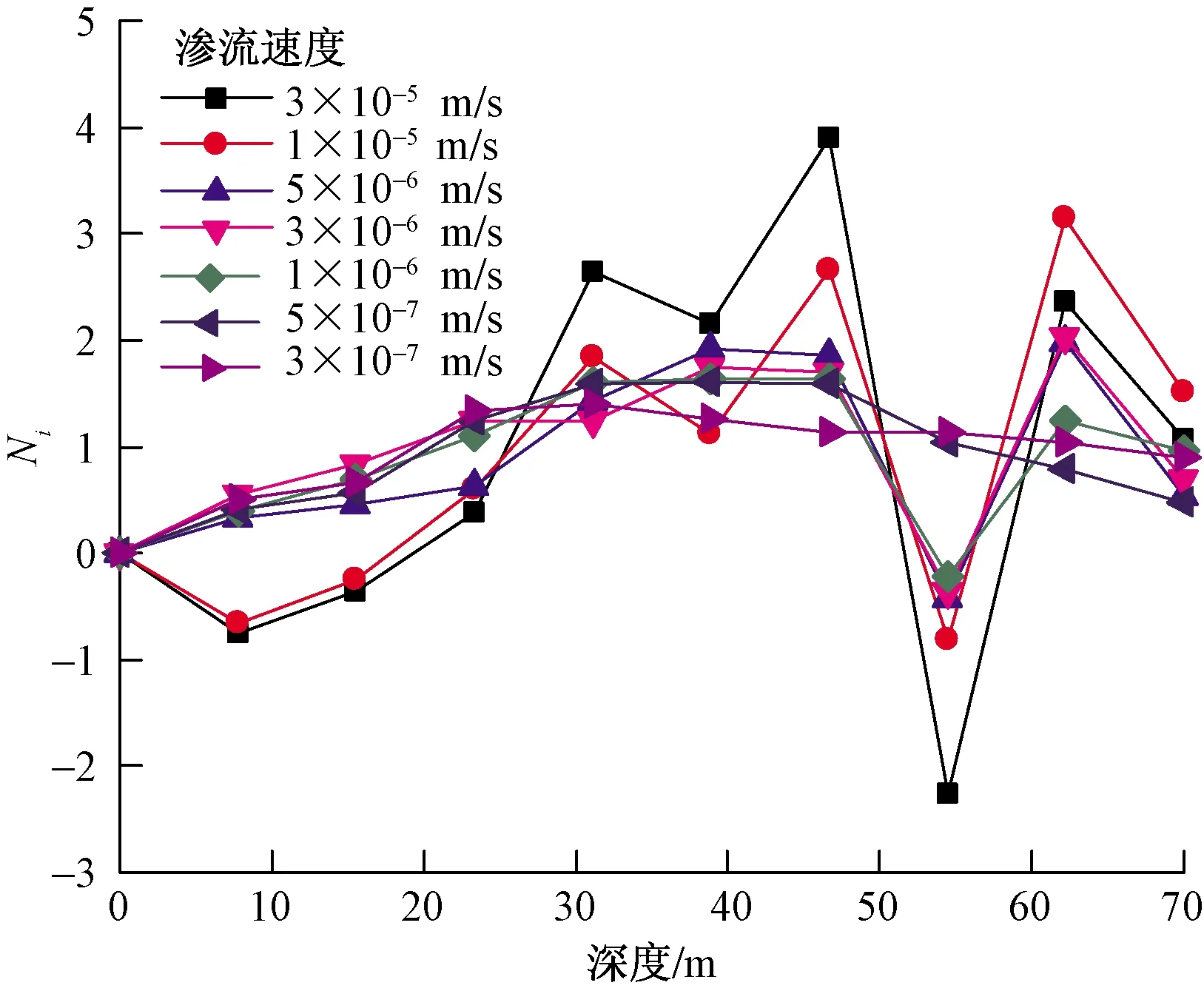
图7 不同渗流速度下的Ni
随着渗流速度逐渐增大,典型含水层厚度先增大后保持不变,在1×10-6m/s时达到最大,约为30 m。当渗流速度小于1×10-6m/s时,整个埋管的各层换热量接近平衡,不会出现Ni<0的情况。这可能是因为较低的渗流速度对埋管换热量作用较小,此时地埋管的分层换热量与各层岩土体的导热系数成正比。当渗流速度大于1×10-5m/s时,Ni在0~25 m的范围内小于0,这可能是因为地下水流速较大,含水层的热扩散系数相比上层岩土体更大,温度也更低。经过一段时间的换热以后,含水层将更多的热量转移到上层岩土体,产生热量的堆积,使上层岩土体的换热受到影响。所以,同样存在典型渗流速度,其大小为1×10-6m/s,此时最佳埋深最大,为58 m。当地下水渗流速度大于1×10-6m/s时,会产生比较明显的热回流现象,而且典型含水层厚度也会随着渗流速度的增大而减小;当地下水渗流速度低于1×10-6m/s时,地下水的作用不再明显,埋管的分层换热量和最佳埋深仅受岩土体热物性的影响。
2.3.3 地下水位线对最佳埋深的影响
当渗流速度为1×10-5m/s时,模拟得到地下水位线分别位于埋深23.8、27.6和33.2 m时Ni沿深度变化的曲线。如图8所示,热回流出现的位置随着地下水位线的变化而变化。当地下水位线在23.8 m时,在23.8~27.6 m,由于岩土层导热系数最大,Ni达到最大值4.24。随后Ni稍有下降但仍大于3。在45 m左右Ni骤降,于47.3 m处低于0,即出现明显热回流,此时地埋管最佳埋深约为47 m。当地下水位线在27.6 m和33.2 m时,Ni分别在50.6 m和57.3 m降低为0,最佳埋深分别为51 m和57 m。通过以上分析可以得出:随着地下水位线的提高,地埋管的总换热量增大,出现热回流的位置升高,但是典型含水层厚度并未变,依然为23 m。因此地下水位线高度对典型含水层厚度影响较小,但是地下水位线的提高使得典型含水层所在的位置提高,导致地埋管的最佳埋深变小。
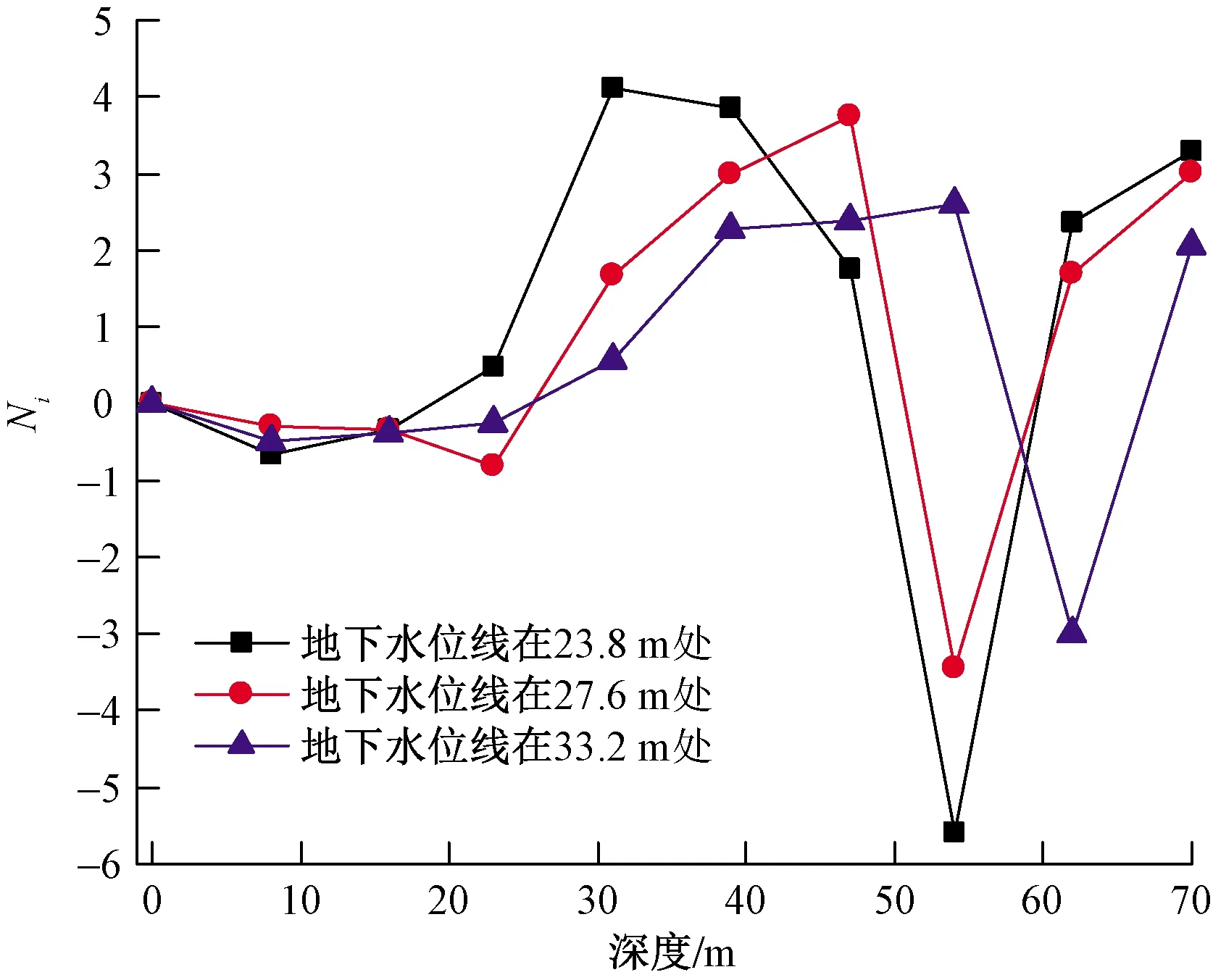
图8 不同地下水位线下的Ni
3 结论
根据黄土高原地区的岩土分层和地下水情况,通过ANSYS建立了单U形竖直地埋管换热器的三维非稳态换热模型。通过与实验数据对比证明了模型的准确性。在不同含水层厚度、地下水渗流速度和地下水位线高度的情况下,利用该模型对循环流体温度沿深度方向的变化、分层换热量和周围岩土体温度响应进行模拟与分析,进而得到地埋管换热器的最佳埋深。结论如下。
(1)在地下水渗流的作用下,地埋管埋深过大会出现热回流现象,导致埋管后半部分多为无效换热。
(2)存在典型含水层,当实际含水层的厚度不超过典型含水层厚度时,地埋管最佳埋深的位置为实际含水层底部;当含水层厚度超过典型含水层厚度时,地埋管最佳埋深的位置为典型含水层的底部;在黄土高原地区,渗流速度为1×10-5m/s时,典型含水层位于埋深27.6~50.6 m处。
(3)分别对渗流速度为3×10-5、1×10-5、5×10-6、3×10-6、1×10-6、5×10-7、3×10-7m/s的7种情况进行模拟与分析,得出当渗流速度大于1×10-6m/s时,典型含水层的厚度随渗流速度的增大而减小,在1×10-6m/s达到最大值30 m;当渗流速度小于1×10-6m/s时,地下水不再是地埋管换热的主要影响因素,最佳埋深仅受岩土体热物性的影响。
(4)分别对地下水位线位于埋深23.8、27.6、33.2 m的情况进行模拟,得到地下水位线高度对典型含水层的厚度影响较小。但是地下水位线越高,典型含水层所在的位置就越高,最佳埋深也就越小。
