基于改进粒子群优化-反向传播神经网络算法的小麦储藏品质预测模型

2021-08-20蒋华伟

科学技术与工程 2021年21期

蒋华伟, 郭陶, 杨震

(1.粮食信息处理与控制教育部重点试验室(河南工业大学)，郑州 450001；2.河南工业大学信息科学与工程学院，郑州 450001)

小麦在储藏过程中，其品质会随着环境的变化和储存时间的延长逐渐产生质变甚至劣变，降低了小麦的食用品质和加工价值，造成大量的经济损失，因此可通过研究预测储藏小麦的品质变化来降低其损失，对国民经济具有重要意义。现有的文献资料显示小麦在发生质变的同时其自身的生理生化指标也相应产生一定变化[1]，利用这一特点可以对其品质进行预测。目前，对储藏小麦品质的判别方法主要有外观特性分析[2]、食用品质分析[3]以及通过仪器设备对其各项指标进行检测来判断其品质的变化等，如邵小龙等[4]将LDA模型用于软X射线图像数据处理时，对小麦品质判别的准确率达到了95%以上，但是对有幼虫侵蚀小麦的品质判别效果不理想；张红涛等[5]通过显微电子计算机断层扫描(computed tomography，CT)图像对不同虫期的小麦样本进行研究，可及时发现麦粒的早期浸染，但该方法扫描时间长，从而使得小麦品质评价效率较低。这些方法人工和时间成本较高，且主观性强，评价体系烦琐，忽略了小麦自身各生理生化指标之间的相互作用及外部环境产生的影响，因此研究一种新的技术来判别小麦品质至关重要。近年来，随着人工智能和计算机技术的快速发展，为研究小麦储藏品质预测提供了新的思路。

反向传播神经网络(back propagation neural network，BPNN)具有良好的自学习和自适应能力，目前大量的实验测试和理论研究表明BPNN算法是一种有效的学习算法[6]。但其在实际应用中会出现收敛速度慢、泛化性能低等缺点[7]。为了提高其预测的准确性，已有学者提出了一些优化算法，如王振东等[8]采用改进天牛群算法优化BPNN的权值和阈值，并采用可变的感知因子及导向性学习策略，来增强算法跳出局部极值的能力；Yan等[9]为提高保险欺诈识别的准确率，采用改进自适应遗传算法来优化BPNN的初始权值，以克服网络易陷入局部极值、收敛速度慢和样本依赖等缺点；另外，梁晓萍等[10]使用改进头脑风暴智能算法对BPNN进行优化，自动搜索网络的初始权值和阈值，避免网络陷入局部最优，增加网络的收敛速度，从而提高图像还原质量；此外，段秀娟[11]基于混沌粒子群对BPNN进行优化，用于网络安全的风险评估，减小了相对误差，提高了评估的准确率；Xiao等[12]利用粒子群算法的全局搜索能力对BPNN的权值和阈值进行优化，用于齿轮箱的故障诊断。这些方法在一定程度上能够优化BPNN的性能，但搜索速度较慢，为得到精确的解需要花费较多时间，特别是采用粒子群优化算法(particle swarm optimization，PSO)优化BPNN，不仅稳定性较差，且由于PSO算法中粒子习惯聚集于自身历史极值或群体历史极值，容易陷入局部极值，并出现早熟收敛、停滞等现象[13-14]。

为了克服上述PSO算法优化BPNN存在的缺点，现通过动态调整PSO算法中的惯性权重和学习因子，使惯性权重和学习因子随着迭代次数的增加而相应变化，使用改进后的PSO算法优化BPNN中的权值参数，建立一种改进PSO算法优化的BPNN预测模型(improved PSO-BPNN，IPSO-BP)，以实现高效准确预测小麦储藏品质的目的。

1 算法描述

1.1 BPNN算法

BPNN通过对样本数据反复训练，不断更新网络的权值和阈值，减小其训练误差，从而逼近期望值。其基本结构如图1所示。

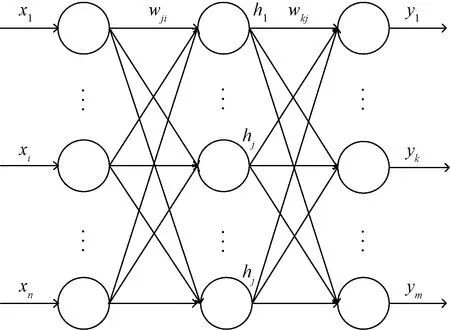
x1,x2,…,xi,…,xn为BPNN的输入；wji为输入层节点i和隐含层节点j之间的权值；hj为隐含层节点的输入值；wkj为隐含层节点j和输出层节点k之间的权值；y1,y2,…,yk,…,ym为BPNN的输出

将训练样本输入模型，依次经过输入层、隐含层和输出层进行处理，得到模型的输出。其中隐含层的输出hj和输出层的输出yk的表达式分别为

(1)

(2)

式中：b1、b2分别为输入层和隐含层的阈值；f()为激活函数。

(3)

根据目标函数计算BPNN模型的误差，当误差不小于指定值时，将误差从输出层向隐含层、输入层逐层传递，并按照随机梯度下降算法更新其权值和阈值，如式(4)和式(5)所示，目标函数如式(6)所示，即

(4)

(5)

(6)

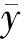
1.2 粒子群算法

在PSO算法中，对分布在d维空间中的n个粒子，第i个粒子的位置为Xi=(xi1,xi2,…,xid)，飞行速度为Vi=(vi1,vi2,…,vid)，其中xid、vid为粒子i在第d维的分量；Pi=(pi1,pi2,…,pid)为粒子i到目前为止搜索到的最优位置，即个体极值Pbest；gi=(gi1,gi2,…,gid)为粒子群目前搜索到的最优位置，即全局极值gbest。

粒子在迭代过程中，通过个体极值和全局极值更新其自身的飞行速度和位置，表达式为

(7)

(8)

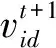
2 改进PSO算法优化的BPNN模型

2.1 惯性权重的改进

PSO算法中使用惯性权重来平衡粒子的局部和全局搜索能力。当其取较大值时，不易陷入局部极值，可增强算法的全局搜索能力；反之能加快算法的收敛速度，提高算法的局部搜索能力。

为了保证粒子在迭代前期拥有良好的局部搜索能力，同时在后期又可以快速收敛，可以对惯性权重ω进行动态调整，常采用线性递减策略调整惯性权重，即

ω(t)=ωmax-(ωmax-ωmin)t/tmax

(9)

式(9)中：ωmax为惯性权重的最大值；ωmin为惯性权重的最小值；t为当前的迭代次数；tmax为最大迭代次数。由于PSO算法中粒子的搜索过程是非线性且复杂的，为更好反映出粒子的实际搜索过程，采用非线性函数动态调整惯性权重，表达式为

ω(t)=ωmax-(ωmax-ωmin)×

[2/(1+e-2t/tmax)-1]

(10)

2.2 学习因子的改进

通过学习因子调节自我认知和群体认知两者之间的比例，以获得全局最优解。在式(7)中，当c1=0时，粒子失去自我认知能力，此时粒子具有扩展搜索空间的能力，并具有较快的收敛速度，但由于缺少局部搜索，对于复杂的问题，比基本的PSO算法更易陷入局部最优。当c2=0时，由于粒子失去了群体认知能力，粒子之间没有信息交流，群体中的粒子个体盲目的进行随机搜索，进而收敛速度慢，得到最优解的可能性小。

因此合理调节c1和c2的大小，可以调整粒子的自我认知和群体认知能力在速度更新中所占的比重。在迭代早期，主要考虑粒子的自我认知能力，在迭代后期，群体认知部分占主导地位，从而使整个过程有利于全局最优解的收敛和精度的提高。因而在算法初期使用较大的c1和较小的c2，然后逐渐减小c1并增大c2，可以实现在初期粒子能够在局部范围内进行比较细致的搜索，同时随着c1的减小使其不易陷入局部极值，而在算法后期则可以提高算法的收敛速度。采用改进后的式(11)和式(12)来调整，表达式为

c1(t)=(c1e-c1s)(t/tmax)2+c1s

(11)

c2(t)=(c2e-c2s)(t/tmax)2+c2s

(12)

式中：c1s和c1e分别为c1的初始值和终止值；c2s和c2e分别为c2的初始值和终止值；t为当前的迭代次数；tmax为最大迭代次数。

2.3 IPSO-BPNN模型

基于上述动态惯性权重和学习因子，采用式(13)来改进PSO算法中的粒子飞行速度，表达式为

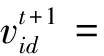
(13)

使用IPSO-BPNN模型，使其在训练前期不易陷入局部极值并在后期快速收敛。该模型的具体训练过程如下。

步骤一初始化IPSO-BP模型的结构，随机生成一群粒子。

步骤二计算各粒子的适应度值fitness。

步骤三更新粒子的个体极值和全局极值。

步骤四如果未达到终止条件则进行下一步，否则结束。

步骤五使用式(13)和式(8)更新粒子的速度和位置。

步骤六输入一组数据，根据式(2)计算模型的输出，根据式(6)计算误差值。

步骤七如果达到训练次数则进行步骤三，否则进行步骤六。

IPSO-BPNN模型流程如图2所示。

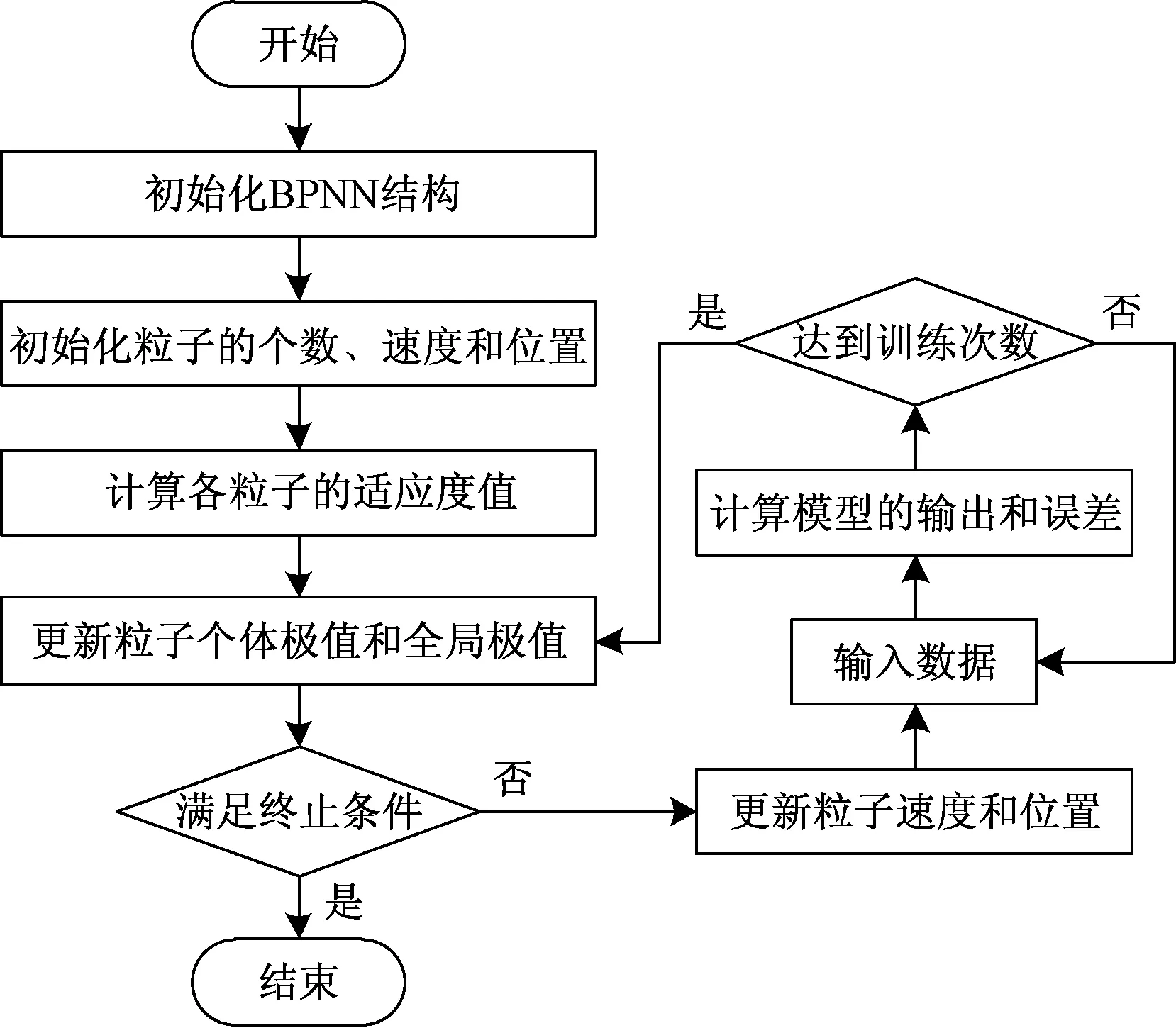
图2 IPSO-BPNN模型训练过程

3 实验分析

3.1 实验材料

选用河南省农科院培育的周麦22和郑麦9023进行实验，并将小麦分为优良、中等和劣质3类，在进行实验时分别对应1、0、-1。同时选取降落数值、脂肪酸值、电导率、发芽率、过氧化氢酶、还原糖和丙二醛7个生理生化指标对小麦储藏品质进行分析。

3.2 小麦指标相关性分析

小麦7个生理生化指标之间存在复杂的相互关系，所表达的信息也具有很大的差异，因此在对小麦储藏品质进行预测之前需要对各指标数据进行相关的预处理以选取最佳指标。

由于小麦各指标在数量级上具有差别，同时为了简化计算过程，在对小麦进行相关性分析之前需要对各指标数据进行标准化处理。使用min-max标准化方法对各指标原始数据进行归一化处理，表达式为

(14)

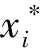
对数据进行标准化处理后，使用式(15)的曼哈顿距离计算分析各指标间的相似性，计算结果如表1、表2所示，曼哈顿距离越小说明两个指标越相似，公式为

(15)

由表1、表2可知，在周麦22和郑麦9023中降落数值、脂肪酸值、电导率、还原糖和丙二醛之间的距离较小，表明它们之间相似性更强，在反映小麦储藏品质方面具有一致性；而发芽率和过氧化氢酶之间距离较小，表明它们两者在反映小麦储藏品质方面具有一致性。因此在后续进行实验时，可以根据指标之间的相似性选取合适的指标对预测模型进行训练，以保证小麦品质预测的准确性和可靠性。

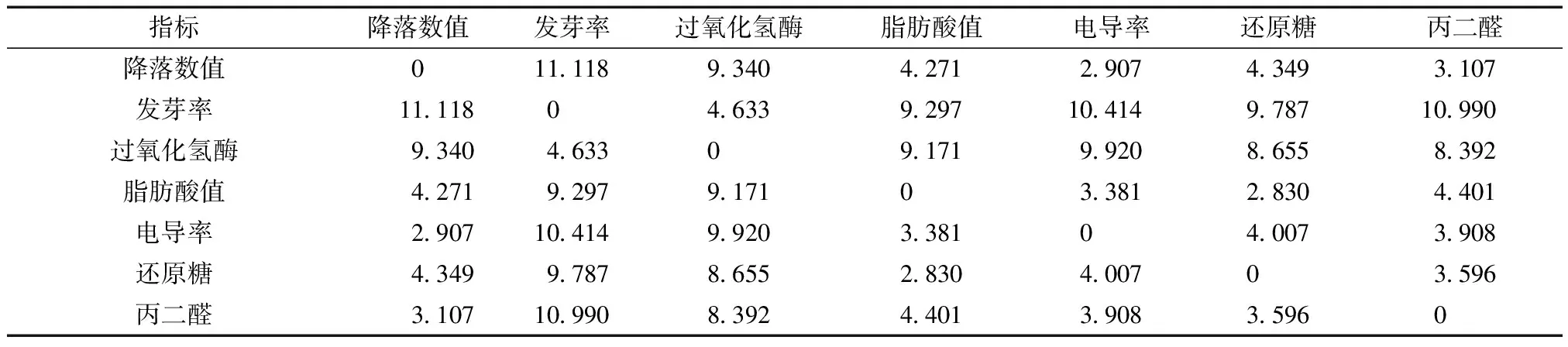
表1 周麦22各指标之间的曼哈顿距离

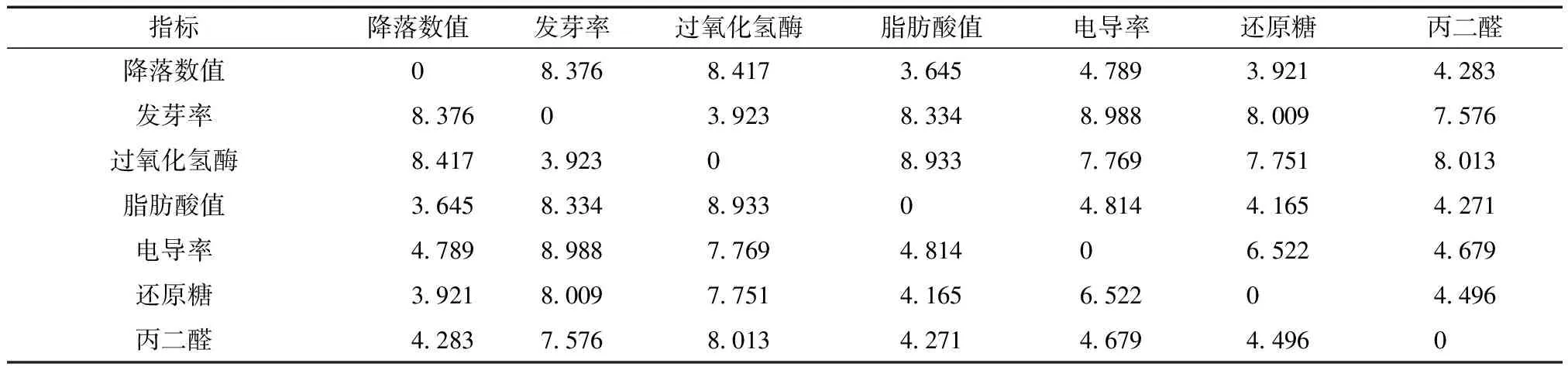
表2 郑麦9023各指标之间的曼哈顿距离

3.3 IPSO-BPNN模型参数优化

BPNN的结构[15-16]和PSO算法中粒子的个数会对实验的结果产生一定影响，因此需要分析不同隐含层神经元个数和粒子个数对IPSO-BPNN模型产生的误差。采用式(16)的均方误差来评价模型的预测效果。预测结果的均方误差越小，表明模型的预测效果越好。

(16)

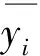
为了分析不同隐含层神经元的个数和粒子的个数对IPSO-BPNN模型所带来的影响，分别分析了采用7个指标和5个指标作为输入数据时的情况，其中输出层的神经元个数为1，隐含层的层数为1，惯性权重的最大值为0.9，最小值为0.4，学习因子c1的初始值为2.75，终止值为1.25，学习因子c2的初始值为0.5，终止值为2.25，最大迭代次数为1 400次；激活函数使用式(3)，目标函数即粒子适应度函数使用式(6)；实验数据采用周麦22。分别计算隐含层神经元个数为6、8、10、12、14，粒子个数为20、30、40时IPSO-BPNN模型所产生的均方误差，其结果如表3和表4所示。

表3 采用7个指标均方误差对比

表4 采用5个指标均方误差对比

由表3和表4可知，当采用7个指标对本文模型进行训练时，其均方误差与采用5个指标进行训练时相比较大，结合表1和表2可知，这是由于发芽率和过氧化氢酶与其他5个指标之间的相似性较低，它们之间可能存在较强的相互作用，用来表达小麦品质时稳定性差，因而具有较大的均方误差。

由表4可知，当隐含层神经元个数为10、粒子数为30时，采用5个指标对本文模型进行训练得到的均方误差最小。当隐含层的神经元个数过少时，IPSO-BPNN模型无法充分学习获得各指标对小麦储藏品质变化的经验表达，从而导致训练的均方误差较大；反之会产生过拟合现象。当粒子数过少时，由于种群的多样性差，易引起过早收敛，从而不易找到全局最优解；反之会使该模型的寻优效率降低。

3.4 IPSO-BPNN与其他模型预测误差对比

为验证本文模型在预测小麦储藏品质上的准确性和可靠性，使用隐含层神经元个数为10、粒子数为30的IPSO-BPNN模型，并采用降落数值、脂肪酸值、电导率、还原糖和丙二醛5个指标作为输入数据，分别在不同迭代次数下对周麦22进行品质预测，将其与BPNN模型和PSO-BPNN模型的预测结果进行比较，结果如图3所示。

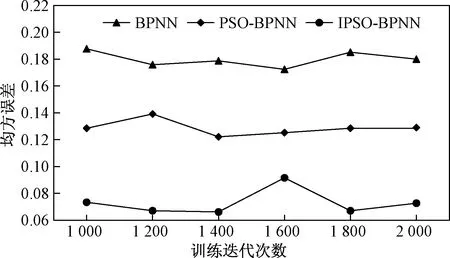
图3 不同迭代次数下3种模型对周麦22预测的均方误差

由图3可知，在不同迭代次数下对3种模型分别进行训练，当迭代次数为1 400次时，相对于其他迭代次数，IPSO-BPNN模型和PSO-BPNN模型预测的均方误差最小，BPNN模型预测的均方误差也相对较小。因此分别采用BPNN模型、PSO-BPNN模型和IPSO-BPNN模型对周麦22和郑麦9023的小麦品质进行预测，其中模型的迭代次数设置为1 400。结果如表5和表6所示。

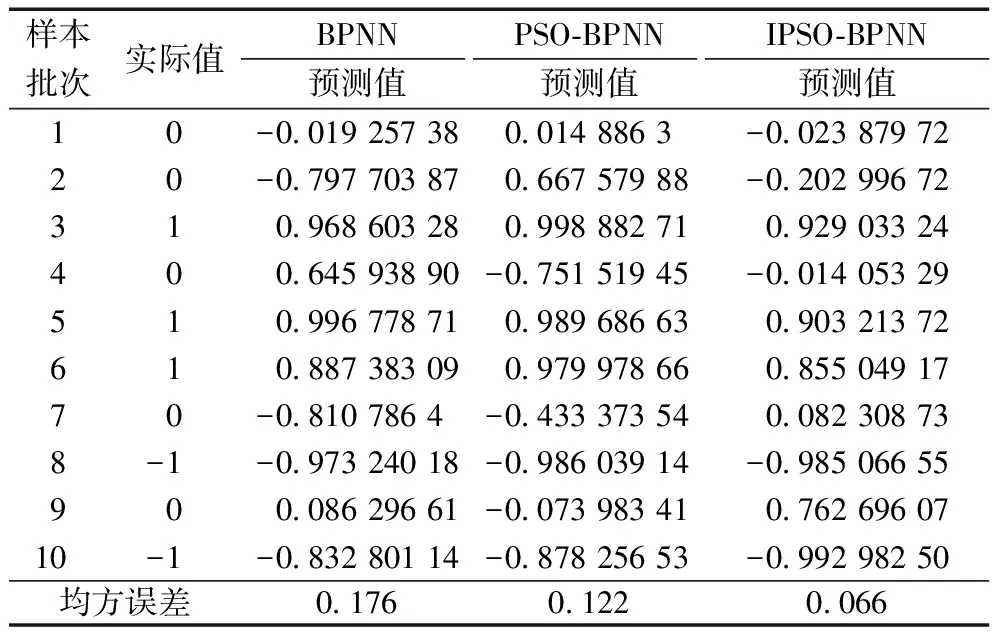
表5 周麦22在3种模型下的预测结果

由表5可知，使用BPNN、PSO-BPNN和IPSO-BPNN对周麦22小麦品质进行预测的均方误差分别为0.176、0.122和0.066；由表6可知，3种模型对郑麦9023小麦品质预测的均方误差分别为0.179、0.089和0.019。由此可以看出与BPNN和PSO-BPNN相比，IPSO-BPNN降低了预测值与实际值之间的均方误差，提高了预测的精度，表明IPSO-BPNN模型在由小麦指标数据预测其品质时，具有更高的精确度和良好的可靠性。