基于跨孔超声波的地下管线埋深精确探测

张秉政,楼国长,沈晓武,陈春飞>

(浙江省工程勘察设计院集团有限公司，浙江 宁波 315012)

1 引 言

地下管线是城市建设与发展的重要基础设施，是城市发展的“生命线”。由于很多管线铺设资料档案的丢失，地下管线分布不清，城市发展与建设速度加快，越来越多的城建规划部门开展地下管线的探测与排查工作。管线探测从实质上来说是对管线做精确的定位与定深[1]，其物理基础是管线与周围介质的物性差异。目前工程上采用的方法主要有电磁感应、地质雷达、地震映像、高密度电法、磁梯度等[2]，其中又以电磁感应法最为普遍[3]。

目前，随着非开挖敷设管线技术的应用和对地下空间开发利用的需求，地下管线愈埋愈深进而要求探测精度愈来愈高，这就给管线探测提出了更高的要求[4-9]。在当前的很多城市工程施工中，如在原有管线位置进行二次非开挖敷设或通过地铁盾构，都需要获取原有管线的精确埋深，有些工程甚至要求精度在10 cm以内。

一般而言，在地表进行的各类物探方法，能基本确定管线的水平位置，但获取的埋深误差较大，且误差随着埋深的增加而增大。如电磁感应法中的直读法、45°法和70%法都存在易受干扰、深埋误差大的缺陷，探地雷达法[10]与地震映像法[11]都需要预设土层波速来判断深度。这些在地表观测数据的方法虽然简单、经济，但都无法精确地确定地下管线的埋深。目前在工程实践中，当工程需要管线埋深的精确资料时，常用方法为探摸法。该方法采用钻机在管线上方直接开钻，通过钻探深度确定管线埋深。显然，该方法易破坏管线，存在较大的工程风险，同时由于管线的圆形形态，也会存在最大达二分之一管径的误差。井中磁梯度法也可应用于解决该问题[12，13]，但仅局限于探测金属管线，同时要求钻孔非常靠近目标管线，因此其应用并不广泛。

为了解决地下管线埋深的精确探测问题，本文提出一种采用跨孔超声波的新的方法技术。超声波法在岩土工程领域有着广泛应用，如用于室内岩体波速测试[14]、工程勘察中原位波速测试以及桩基检测等[15-17]，其具有准确、高效、经济、抗干扰强等优点。本文将超声波法应用于地下管线探测，以解决管线埋深的精确探测问题。其主要原理是在相邻钻孔的同一水平深度上，发射并接收脉冲超声波，通过走时、频谱及波形等参数来分析通过介质的物性特点，以此确定管线的埋深。本文对含管线地层进行了超声波数值模拟，并通过工程实例验证了该方法准确、可靠。该方法对管线探测与排查、以及城市建设施工具有重要的工程意义与价值。

2 方法原理

地下管线实际上是一种“人造异常体”，因此从探测的角度来看，它具有以下几个特点：①埋深不会很大，一般在几米至十几米之间，个别会达到几十米[3]，且一般位于土层之中；②对管线的大概位置与可能走向有一定的预判；③管线的用途以及施工工艺、材料一般已知，即使未知也种类有限，基本可以判断；④大部分的管线都是圆形截面。管线这些“人造异常体”的特点使得管线探测有别于一般的物探工作，实质上是提供了一系列的先决条件，充分利用这些先决条件，结合传统物探的理论与技术，发展一种准确、快速、经济、普遍适用的方法，对城市工程建设十分有必要。

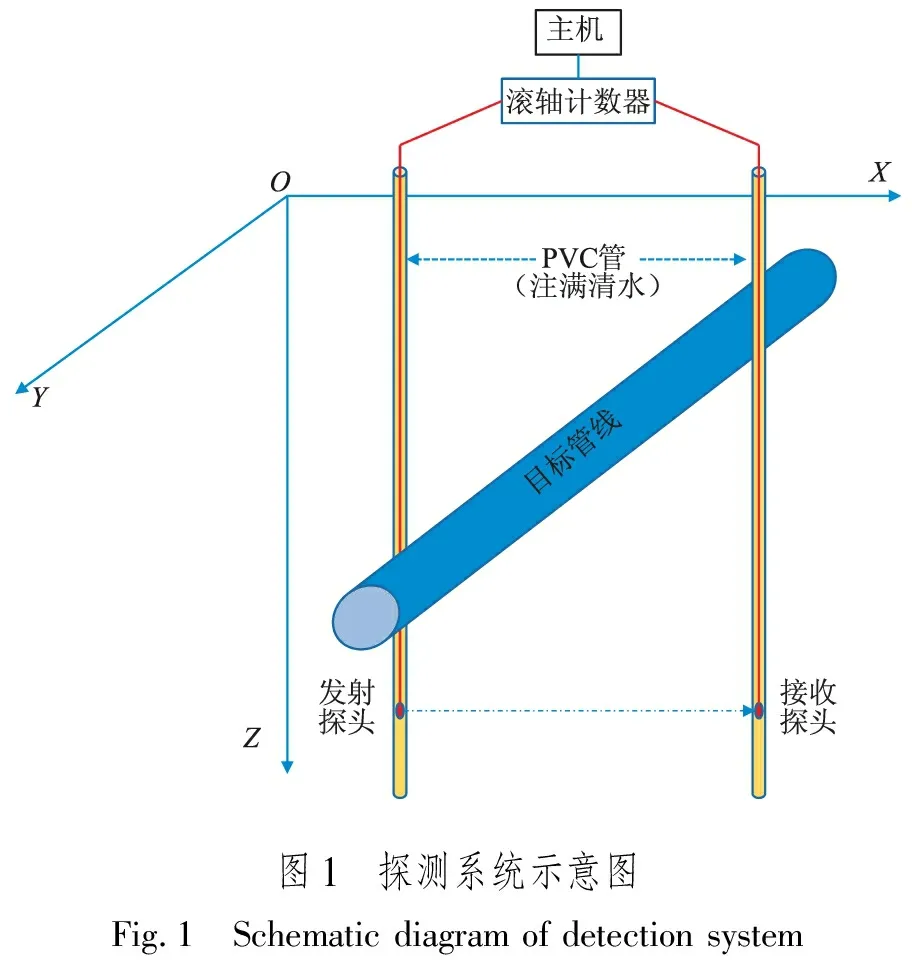
根据管线的特点，本文设计的主要思路是：通过资料调查或传统方法大致确定目标管线的位置和走向后，在目标管线两侧用钻机开孔，在两孔同一深度处，一侧发射超声波另一侧接收，通过分析跨孔超声波的初至时间、波形特点等参数，推断目标管线的精确埋深。整个观测系统如图1所示，主要包括主机、滚轴计数器、超声波探头及标有刻度的连接线等。探测过程中，先在目标管线两侧一定安全距离外开孔，孔中放入PVC管，管内注满清水。之后将发射与接收探头置于管中同一深度，其连接线经滚轴计数器与主机相连，直接采用人工拉线使收发探头同步位移，仪器按设定步长向上自动采集，一般间隔0.05 m或0.025 m记录一道数据。

由于管线材质一般为混凝土或钢材，其波速大于土层波速，超声波从发射探头出发至接收探头，主要路径有四种(图2)：①直达波，超声波直接穿过土层；②反射波，超声波经管线反射；③上行折射波，入射波达到折射波临界角，沿管线上沿传播；④下行折射波，入射波达到折射波临界角，沿管线下沿传播。设土层波速为vps，管线波速为vpp，管线半径为R，左侧探头与管线中心的水平距离为L1、垂向距离为S，右侧探头与管线中心的水平距离为L2、垂向距离为S，以上物理量波速单位都为m/s，距离单位为m。若已知管线波速和土层波速，则根据斯奈尔定律可以确定折射波临界角α。

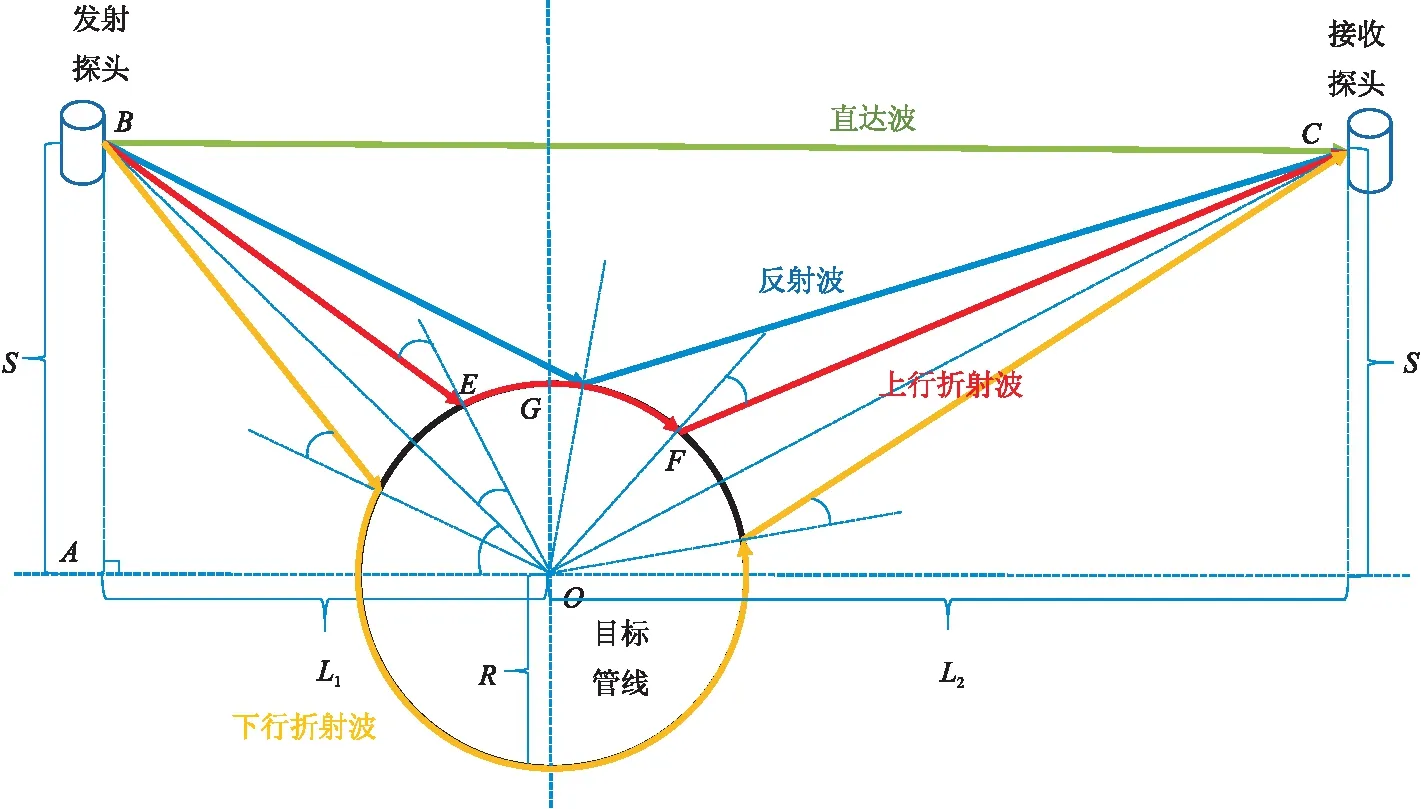
图2 超声波路径图Fig.2 Ultrasonic wave path diagram

计算图中超声波四种路径的走时：

1)直达波走时

2)反射波走时

该观测系统中，反射波路径都大于直达波，因此其初至在直达波之后，由于该方法中发射的超声波为连续脉冲，因此较难分辨直达波后的反射波。

3)上行折射波走时

折射波的入射角和出射角相同，设为α，且系统左右两侧计算过程相同，利用余弦定理可得如下关系：

可求得|BE|的值：

(1)

利用正弦定理可得如下关系：

可求得|β|值：

则圆弧EG(G点为圆心O作地面的垂线相交于管线外径上的点)的弧长为：

|EG|=R(π/2-β-γ)

(2)

其中,γ=arctam(S/L1)。利用相同的方法可以求得系统右侧的路径长度：

(3)

|GF|=R(π/2-β′-γ′)

(4)

其中：

γ′=arctan(S/L2)

由此，可以计算得到上行折射波的走时，单位s：

(5)

4)下行折射波走时

下行折射波走时的计算过程与上行折射波相同，此处不再赘述。

跨孔超声波法通过分析超声波的走时变化来判断是否存在管线、管线的埋深等问题。按照上述模型，需要确定折射波成为初至波的条件。

3 走时初至模拟

3.1 钢制管线的走时初至分析

基于工程勘察中的先验信息，取目标钢制管线的波速为5 800 m/s，土层波速为1 400 m/s，设管线埋深为10 m，探测步长为0.1 m。设计了两种管径(1.0 m和0.3 m)的观测系统，计算不同L1和L2下初至的时间。计算结果见图3，其中图3(a)、图3(b)的目标管线管径为1.0 m，图3(c)、图3(d)的目标管线管径为0.3 m。

图3 钢制管线的直达波和折射波走时模拟Fig.3 Travel time simulation of direct and refraction wave in steel pipeline

通过对图3走时计算结果的分析发现，初至波有以下几点特征：①直达波的初至反映了土层的波速，当土层无变化时始终保持一致；②在目标管线影响的一定范围内，折射波的走时小于直达波走时，整体波形的初至面出现凸起形态；③上行折射波与下行折射波对于管线中心线对称，由此产生了“双峰”的现象，双峰形态随目标管线管径的增大或跨孔距离的减小而愈发明显，如图3(a)明显于图3(b)，而在图3(c)和图3(d)中由于管径较小而不明显；④由初至面凸起形态可精准地判断目标管线的深度，当双峰形态明显时取双峰的中间点，当不明显时直接取最小时间点。

3.2 混凝土管线的走时初至分析

基于工程勘察中的先验信息，取目标混凝土管线的波速为3 800 m/s，土层波速为1 400 m/s，设定管线埋深为10 m，探测步长为0.1 m。设计了两种管径(1.0 m和0.3 m)的观测系统，计算不同L1和L2下初至的时间。计算结果见图4，其中如图4(a)和图4(b)的目标管线管径为1.0 m，图4(c)和图4(d)的目标管线管径为0.3 m。

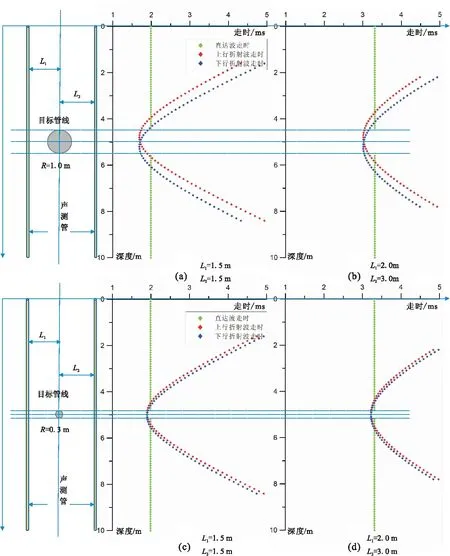
图4 混凝土管线的直达波和折射波走时模拟Fig.4 Travel time simulation of direct and refraction wave in concrete pipeline

从图4来看，混凝土管线的初至面特征与钢制管线基本一致，也可以通过初至面凸起处双峰的中点来精确地确定管线的埋深。当管径较小时，双峰现象不明显，此时峰值最小时间位置对应于管线深度。

通过对钢制管线与混凝土管线的跨孔超声波走时分析，表明该方法可以精确地探测地下管线的埋深，且探测误差不随管线埋深的增加而增加。另外，由于钻孔是在土壤中进行，一般来说倾斜度不大，因此该影响较小。理论上来说该方法的初至面都会产生双峰现象，可通过双峰的中点来判定管线中心埋深。但是当管径较小时，双峰现象不明显，此时可直接将最小走时点判定为管线中心埋深。此外，在管线范围外且折射波初至靠前的区域，可同时观测到折射波与直达波的存在，由此也可判断出上下两处临界深度，该深度直达波与折射波走时基本相同，通过取两处临界深度的中间点也可判定管线埋深。

4 工程实例

为了验证跨孔超声波法的准确性，对一系列的工程实例进行了分析。采用武汉岩海公司生产的RS-ST06D(T)型跨孔超声波分析仪。该仪器可实现一发多收，并通过滚轴计数器按设定步长快速地采集数据。

4.1 工程实例1

工区位于宁波，需要探测某天然气管线的精确埋深，管线材质为钢制，直径508 mm。首先采用传统的电磁法初步测出该管线的水平位置与埋深，预估埋深为5～10 m，探测孔深设为15 m。探测孔深一般大于预估埋深3 m以上，以提供足够的背景场。在管线两侧一定安全距离外开孔，孔间距1.9 m。对于跨孔间距的选择不宜过大也不宜过小，过大则信号能量弱，一般大于5 m时信号已经很难分辨，过小则存在安全风险容易破坏管线，一般开孔位置距离管线宜在0.5 m以上。采用跨孔超声波法进行探测，发射信号脉宽40 μs，采样间隔1.6 μs，探测步长0.05 m，图5展示了实测波列分析图。对探测结果做如下分析：

图5 工程实例1:某钢制管线实测波列剖面及分析Fig.5 Engineering case 1: the measured wave form and analysis of a steel pipeline

①0.0～2.75 m为填土层，由于土质松散，超声波易衰减，因此难以接收到信号。

②2.75～6.8 m为一般的土层，从波形上来看为直达波，即使后续存在折射波与反射波，也无法直接分辨。从该区域的波形也可看出直达波形态的基本特征(图5内A框)，即首波相对能量最强，初至清晰，后续波形能量逐渐衰减。

③6.8～7.7 m宏观上呈明显的“双峰”形态，且波形形态有别于一般的直达波，这是最值得关注的范围。在进入该范围时，直达波走时与形态基本不变，而在直达波初至之前开始出现能量较弱、走时较小的波形(图5内B框)。根据跨孔超声波的理论，该波形为超声波经过管线后产生的折射波。图5内C框为该范围波形的放大，其中红色曲线为直达波初至，绿色曲线为折射波初至。上行与下行折射波的峰值点分别位于7.05 m与7.45 m，折射波初至前置的临界位置分别为6.8 m与7.7 m，两者的中点都为7.25 m。由此可以判定管线埋深的中间位置为7.25 m。

④7.7～15.0 m为一般的土层，土层波速略有变化，但显然不存在双峰现象或明显的小范围突变，即该范围内无管线。

通过对图5的分析，可以得出该管线的精确埋深，其中心位置为7.25 m，上下管顶为7.0 m与7.5 m，分辨率为0.05 m。该实例证实跨孔超声波法的理论正确，具有很高的可操作性与精度。

4.2 工程实例2

本工程需要精确地探测某地下污水管的埋深，该污水管直径2 m，材质为混凝土。前期资料的收集基本确定了该管线的水平方位，但对于埋深并不确定，因此采用跨孔超声波法探测该管线的精确埋深。孔间距2.5 m，发射信号脉宽40 μs，采样间隔6.4 μs，探测步长0.05 m，探测孔深14 m。图6展示了该工程的实测波列分析图。

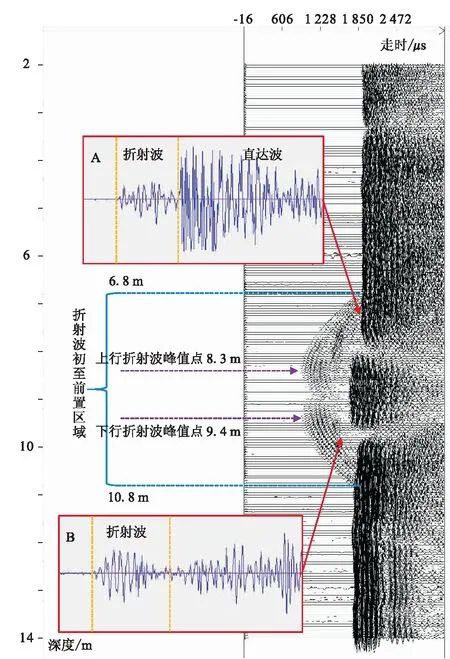
图6 工程实例2:某混凝土管线实测波列曲线及分析Fig.6 Engineering case 2: the measured wave form and analysis of a concrete pipeline

该数据显示出非常明显的“双峰”现象。其中折射波初至前置区域为6.8～10.8 m(中心深度8.8 m)，上下折射波峰值点位置分别为8.3 m和9.4 m(中心深度8.85 m)，两者所判断的管线中心埋深基本一致。

本工程中管线直径大，声测孔间距小，因此观测到的数据中上行折射波与下行折射波的分离非常明显。此外，由于走时差较大，波形中折射波与直达波可明显分离(图6框A)。相对来说，折射波能量较弱而频率有一定的降低。

以上2个工程实例分别解决了金属管线与非金属管线的埋深精确探测问题，所得效果完全满足工程需求。从中也总结出影响探测精度的主要因素：

1)探测步长，根据工程实际需求，设置合理的探测步长，最小可以达到滚轴计数器的最小步长0.01 m；

2)跨孔间距，该因素主要影响超声波信号质量；

3)成孔的垂直度，以上理论是建立在垂直成孔的基础上，实际工程施工中会有一定程度的倾斜。

5 结 论

本文通过理论计算、模型分析与工程实例，详细论述了基于跨孔超声波的地下管线埋深精确探测这一新的方法。该方法基于地下管线的特点，设计跨孔超声波这一观测系统，通过分析初至波前面的“双峰”形态精确计算出管线中心的埋深，从而达到精确探测的目的。该方法具有高精度、操作便捷、安全可靠等优点，具有在深埋管线的精确探测中推广的价值。