将数学史融入初中数学课堂的教学研究

徐兴云

(江苏省连云港市实验学校 222006)

在初中数学教学中将数学史融入数学课堂教学中，改变数学在学生心中的形象，也可以抵消学生对于数学的抵触，从而提高学生学习数学的兴趣，极大限度的理解数学，在快乐中学习数学，这对数学的教育也具有非常大的价值.

一、数学课堂融入数学史的困难

目前来讲，学生获得数学史知识的途径是狭窄的，主要是通过课堂上老师的讲解，这样一来，就提高了对老师的要求.但是通过对很多一线老师的调查发现，即使老师们知道将数学史融入数学课堂的价值和意义，但是绝大多数的老师是不用的.

1.教师数学史教育水平“先天不足”

中学数学教师，特别是中老年数学教师，在他自己的学习期间就很少甚至没有接触过数学史的相关内容，所以在自己教学时也不会注重数学史知识，更不会去学习，势必就造成了很多数学老师不具备数学思想，数学方法论，数学史等方面的知识.所以无法在课堂上引入和应用.

2.教师数学史教育水平“后天缺陷”

随着新课标对数学史的内容和要求都显著增强，提高现有数学教师的数学史水平迫在眉睫，但是对数学教师进行数学史培训很难实施，而且针对教学的数学史课程教材又相当匮乏，现有的一些资源和书籍也无法匹配目前的中学数学教育，所以将数学史融入中学数学教学缺乏系统性和完善性.

二、数学课堂融入数学史的价值

1.数学文化的最佳载体

传统的初中数学教学，学生学习只是简单的记忆，不知道定理和公式的由来，有的老师常常会说“这是规定”，打消了学生的好奇心，久而久之学生就失去了对数学的兴趣.而新课程改革提出了要增加数学文化的内容，因此数学史作为数学概念，数学命题以及作为数学文化的载体，自然就被引入到课堂之中.

2.理解数学的必经之路

数学是一门逻辑性非常强的学科.目前我们所看到的一些概念、解决问题的方法，都是数学家们经过几百年总结出来的，在总结过程中，还产生了一些其它的原理，影响着我们的生活.数学史留给我们的是数学成果，在教学中，融入数学史，可以让学生了解到相应的历史背景.可以说是透过现象看本质，以此来让学生从根本上掌握数学知识.

3.思想教育的良好素材

数学史可以展现我国的历史过程，也可以体现我国古人的文化和智慧，将其融入到教育中，可以让学生们在掌握基本知识的同时，学习到相应的勇气，以及面对困难，不屈不挠的精神.古今中外，有多少数学家不都是经历了一次次失败，才总结出来真理的吗，这些对于学生来说，也是良好的思想教育素材，促使着学生也可以在学习数学过程中，努力、不怕苦的进行学习.

4.激发兴趣的有效途径

很多著名的数学家，都是从兴趣开始最终成为有名的数学家.老师在课堂上研究问题的时候，不要单单只研究解题的方法和思路，还要注重数学课堂的趣味性，通过讲解数学发展的历史，从而引起学生的兴趣，通过一些数学家的故事，让学生了解到数学的学习并不是单单的解题模式，其中还蕴含着历史悠久的故事.这从某种程度上也更加能够激发学生学习数学的兴趣，增加学生学习数学的信心.这样既挖掘了数学的教育价值，又激发了学生的兴趣.

三、数学课堂融入数学史的应用

1.以激发学习兴趣为目的的教学案例设计

实例：在初中数学课本上，学习有理数的乘方时，可以向学生介绍一个关于棋盘麦粒的故事，教师通过对故事的讲解，从而引到数学的教学中去，并结合实际情况进行讲述.在导入新课时，我们可以这样设计：

第一个环节就是讲故事，故事发生在古老的印度，当时的印度国王非常迷恋国际象棋，那就决定这么好玩的象棋，要奖励它的发明者，当时国际象棋的发明者是宰相西萨·班·达依尔.于是国王面对这位大臣就问了他：你想要什么奖励？宰相就说我什么奖励都不想要，只想要一些米，这样吧，在我发明的国际象棋台上面，第一格放一粒米，第二个放两粒米，以此类推，每一格都比前一格加一倍直到把象棋的64格摆满为止，国王想都没想就答应了，这也太容易了，当真正摆起来的时候，国王才发现，如果把全球的米粒都放在棋盘上也不够放，国王羞愧的低下了头.

第二个阶段就是提出问题，让学生们发散思维，想一下米粒到底有多少？从而引出这节课学习的内容：有理数的乘方.通过学习这节课的知识，就能够很好的解决这个问题.

这种方式与传统的教学模式相比，能够很大的激发学生的好奇心和学习的热情，也激发了学生在学习中探索和思考的过程.

2.以开拓视野为目的的教学案例设计

实例：在讲解八年级上册《勾股定理》这一节课中，可以这样设计：

勾股定理是几何学中的明珠，所以它充满魅力，千百年来，人们对它的证明趋之若鹜，其中有著名的数学家，也有业余数学爱好者，有普通的老百姓，也有尊贵的政要权贵，甚至有国家总统.也许是因为勾股定理既重要又简单，更容易吸引人，才使它成百次地反复被人炒作，反复被人论证.

中国古代最早对勾股定理进行证明的，是三国时期吴国的数学家赵爽.赵爽创制了一幅“勾股圆方图”，用数形结合的方法，给出了勾股定理的详细证明.

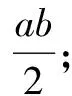
赵爽的这个证明可谓别具匠心，极富创新意识.他用几何图形的截、割、拼、补来证明代数式之间的恒等关系，既具严密性，又具直观性，为中国古代以形证数、形数统一、代数和几何紧密结合、互不可分的独特风格树立了一个典范.

这样，不仅使得学生们感受数学家们的思想，也能够从中学习到解决问题的办法，并能够在以后的学习中学习和应用.之后可以鼓励学生仿造这种拼接的思想另寻证明途径，从而启发学生的思维.

四、数学课堂融入数学史的延伸

有些数学的历史发展比较远，所涉及的知识面也就比较广，数学史的知识可以让学生们在课外生活中了解，也可以在日常的生活中，师生之间多多交流.

比如，在课余活动的时间里，多开展一些有关于数学史的活动；建立一些数学史的文化氛围；通过黑板报，请数学名人开讲座和建立数学文化班级群等方式，引起学生们的讨论和学习的热情，在数学发展历史上，学习数学家的精髓，提高学生的个人素质和文化素养.

数学史的融入并不仅仅只是为了让学生知道这么一段历史，更多的是为了让学生通过数学史学会数学思想，增加学习兴趣，感受知识本质，以及能感受到数学史带给我们的教育价值.作为教师要多做研究，能够使得数学史在课堂上的融入达到“随风潜入夜，润物细无声”般潜移默化的效果，方为最佳境界.