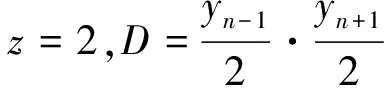Pell方程组x2-(k2+k)y2=1,y2-bz2=4的公解
2021-08-19罗长盛
罗长盛
(西华师范大学数学与信息学院,四川南充 637009)
0 引言
目前人们对于Pell方程的研究已经取得了相当丰富的成果,但对于Pell方程组的求解问题还未被完全解决,近年来人们对Pell方程组
(1)
的求解问题做了许多的研究:

本文讨论了,当k=7,b为偶数时方程组(1)的公解的情况,得到了如下结论.
定理令p1,…,ps(1≤s≤4)为互异的奇素数,当b=2p1…ps,1≤s≤4时,方程组
(2)
当b=2×449时方程组(2)有非平凡解(x,y,z)=(±13 455,±1 798,±60);当b≠2×449时方程组(2)仅有平凡解(x,y,z)=(±15,±2,0).
1 引理
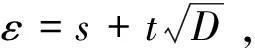
引理1.2[15]当a>1并且a是一个平方数,此时方程ax4-by2=1,x,y∈N最多有一组解.

引理1.4设(x1,y1)是Pell方程x2-Dy2=1的基本解,则x2-Dy2=1的所有正整数解,可由下式给出
引理1.5(1)不定方程x4-56y2=1只有整数解(x,y)=(±1,0).
(2)不定方程225x4-56y2=1只有整数解(x,y)=(±1,±2)
(3)不定方程x2-224y4=1只有整数解(x,y)=(±15,±1),(x,y)=(±1,0).
证明(1)因为Pell方程x2-56y2=1的基本解是(x1,y1)=(15,2),由引理1.4得x2=449,由于15,449均不为平方数,则由引理1.1得方程x4-56y2=1只有一组平凡解(x,y)=(±1,0).
(2)由引理1.2知,方程225x4-56y2=1最多有一组正整数解,因为(1,2)为方程225x4-56y2=1的正整数解,所以方程225x4-56y2=1只有整数解(x,y)=(±1,±2).
(3)因x2-224y2=1的基本解是(15,1),但是y2=2x0=30是非平方数,由引理1.3得方程225x4-56y2=1仅有一组正整数解,(15,1),故方程225x4-56y2=1仅有整数解(x,y)=(±15,±1),(±1,0).
引理1.6易知(15,2)为Pell方程x2-56y2=1的基本解,令Pell方程x2-56y2=1所有解为(xn,yn),n∈Z,任意的xn,yn具有下面的性质:
(1)xn+2=30xn+1-xn,x0=1,x1=15 ,yn+2=30yn+1-yn,y0=0,y1=2
(2)xn+1=15xn+112yn,yn+1=2xn+15yn,yn-1=15yn-2xn,y2n=2xnyn
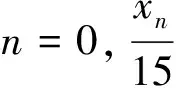
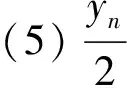
(6)xn≡1(mod2),x2n≡±1(mod15),x2n+1≡0(mod15),y2n≡0(mod4)
y2n-1≡2(mod4),y2n+1≡±2(mod15),y2n≡0(mod15)
(7)gcd(xn,yn)=1,gcd(xn,xn+1)=1,gcd(yn,yn+1)=2
gcd(x2n,y2n+1)=gcd(x2n+2,y2n+1)=1,gcd(x2n+1,y2n)=gcd(x2n+1,y2n+2)=15
证明Pell方程x2-56y2=1的基本解是(x1,y1)=(15,2);根据引理1.4得,∀n∈Z(1)成立,
(2)由引理1.4得∀n∈Z
故xn+1=15xn+112yn,yn+1=2xn+15yn,同理可得yn-1=15yn-2xn,y2n=2xnyn.
(3)由条件知,∀n∈Z

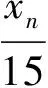

(6)根据引理1.6的(1)可以得出引理1.6的(6)成立.
(7)由方程x2-56y2=1可以知道xn为奇数,yn为偶数,且gcd(xn,yn)=1,根据引理1.6的 (2)和(6)得
gcd(xn,xn+1)=gcd(xn,15xn+112yn)=gcd(xn,112yn)=gcd(xn,yn)=1
gcd(yn,yn+1)=gcd(yn,2xn+15yn)=gcd(yn,2xn)=gcd(yn,2)=2
gcd(x2n,y2n+1)=gcd(x2n,2x2n+15y2n)=gcd(x2n,15y2n)=gcd(x2n,y2n)=1
gcd(x2n+2,y2n+1)=gcd(15x2n+1+112y2n+1,y2n+1)=gcd(15x2n+1,y2n+1)=gcd(15x2n+1,y2n+1)
=gcd(x2n+1,y2n+1)=1
gcd(x2n+1,y2n)=gcd(15x2n+112y2n,y2n)=gcd(15x2n,y2n)=gcd(15,y2n)=15
gcd(x2n+1,y2n+2)=gcd(x2n+1,2x2n+1+15y2n+1)=gcd(x2n+1,15y2n+1)=gcd(x2n+1,15)=15
2 定理的证明
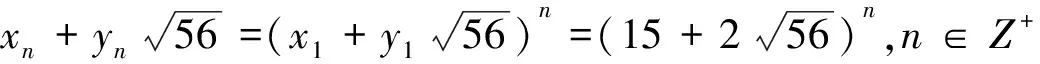
设(x,y,z)=(xn,yn,z)是方程组(1)的正整数解,由引理1.6的(3)有
(3)
情形1当n为正奇数时,令n=2m-1,m∈Z+,由引理1.6的(2)此时(3)可化为
(4)
当m=1时,(4)式化为Dz2=4x0y0x1y1=0,则z=0,此时方程组(2)仅有平凡解(x,y,z)=(±15,±2,0)
当m=2时,(4)式为Dz2=4x1y1x2y2=4×15×2×449×60=602×2×449,因此可得z=60,
D=2×449故方程组(2)的正整数解解为(x,y,z)=(13 455,1 789,60)则方程组(2)的非平凡解为(x,y,z)=(±13 455,±1 789,±60).
当m∈z+,m≠1并且m≠2,对m分情况讨论:
情形1.1当m是正偶数且m≠2,根据引理(1.6)的(7)可得
gcd(xm-1,ym-1)=gcd(xm,ym)=1,gcd(xm-1,ym)=15,gcd(xm,ym-1)=1
gcd(xm,xm-1)=1,gcd(ym,ym-1)=2
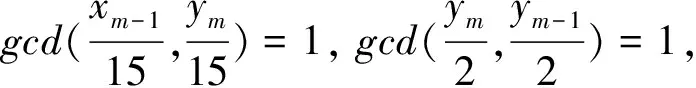
这与D的假设矛盾,故此时方程组(2)无正整数解
情形1.2当m为正奇数且m≠1,根据引理1.6的(7)可得
gcd(xm-1,ym-1)=gcd(xm-1,ym)=1,gcd(xm-1,ym)=1 ,gcd(xm,ym-1)=15,
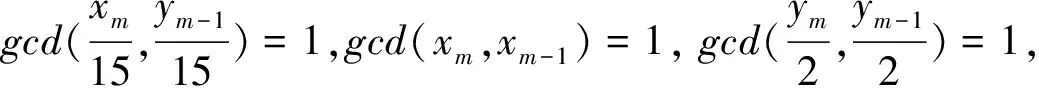
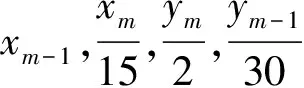
令m=2k-1.k∈Z+并且k≥2,则有
Dz2=4x2(k-1)y2(k-1)x2k-1y2k-1
(5)
根据引理1.6的(2)知(5)式可化为
Dz2=8x2(k-1)xk-1yk-1x2k-1y2k-1
(6)

情形1.2.1当k为正奇数且k≠1,令k=2l-1,l∈Z+,l≥2,将k=2l-1带入(6)式得
Dz2=8x4(l-1)x2(l-1)y2(l-1)x4l-3y4l-3
(7)
根据引理1.6的(2)知(7)式可化为
Dz2=16x4(l-1)x2(l-1)xl-1yl-1x4l-3y4l-3
(8)
取l=2,由(8)式可得,Dz2=16×43 201×449×15×2×12 082 575×1 614 602,即
Dz2=26×32×53×11×19×61×79×191×139×449×929×2 111
故可解的z=120,D=5×11×19×61×79×191×139×449×929×2111,此时D与题设矛盾,因此方程组(2)不存在正整数解.


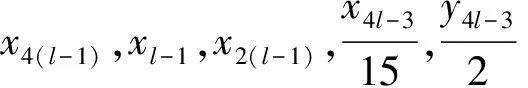
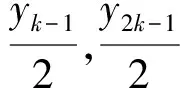
情形2n是正偶数的情况下,由引理1.6的(6)可知