风扇/压气机静子周向限位失效对气动性能的影响

张华军，李晓军，吴学岗，李 兵

(1.空装成都局某军事代表室，成都 610500；2.中国航发四川燃气涡轮研究院，成都 610500)

1 引言

随着飞机向多用途、高机动性方向发展，其发动机应具备宽任务包线、高推重比和低油耗的工作能力。为此，压缩部件必须实现高负荷、高效率和高稳定性的设计指标[1-4]。而设计指标的大幅提升，不仅对压缩部件级间参数的设计匹配带来一定挑战，同时也使得转子和静子叶片承受更大的气动力，增加了静子周向限位失效所诱发的级间匹配失谐风险。

在多级轴流压气机设计中，各级间匹配的好坏直接决定了压缩部件性能的优劣，级间匹配是设计工作的重中之中，也是严重困扰发动机研制的一大难题[5-11]。基于仿真和试验的手段，众多学者开展了大量的压缩部件级间参数匹配研究工作，获得了众多具有普适性和重要意义的研究结论，为压缩部件的设计及改进指明了方向。章石波[12]、刘昭威[13]、陈江[14]等认为，任意级的级间参数选择不合适将导致该级的性能降低，甚至影响其他多排叶片的工作状态，使之偏离设计状态，进而导致压气机整机性能无法达到设计目标。还有学者[15-17]通过对轴流压气机多级匹配特性的详细研究，认为压气机的压比、效率随流量的变化关系及喘振边界主要受下游部件的影响。但现阶段，级间参数匹配分析的重点仍主要聚焦在多级间的匹配。

压缩部件的匹配设计不仅要关注级与级间的匹配，同时也要关注转子与静子间的匹配。当静子的周向限位措施不当或强度储备不足，而静子叶片承受较大的气动负荷时，将导致静子周向限位失效，进而诱发压缩部件转静子间和级间的匹配失谐——轻者导致压缩部件甚至发动机性能下降，重者将诱发发动机喘振停车。因此，认清静子周向限位失效对压缩部件气动性能的影响机理，掌握其影响程度，对压缩部件和发动机的研制具有重要的意义。目前，国内外关于静子周向限位失效(简称静子限位失效)所诱发的转子、静子间的匹配失谐的研究较少，无法对现有压缩部件和发动机的研制提供高效帮助。

本文以NASA-120859高负荷两级风扇为对象，采用数值模拟方法研究了静子限位失效导致级间匹配失谐、压缩部件性能变化的机理。分析了不同失效转速和不同失效级对压缩部件性能的影响，总结了静子限位失效对气动性能的影响规律，可为压缩部件和发动机的研制提供重要的技术支持。

2 研究对象及数值模拟方法

2.1 研究对象

NASA-120859 高负荷两级风扇采用了跨声速风扇/压气机典型的设计技术，如高叶尖切线速度、高气动负荷和多圆弧叶型，其具体设计参数如图1和表1所示[7]。

表1 NASA-120859两级风扇设计参数Table 1 Design parameter of two-stage fan(NASA-120859)

图1 NASA-120859两级风扇Fig.1 Two stage fan of NASA-120859

2.2 数值模拟方法

数值模拟中，网格的生成和计算均采用CFD商业软件NUMECA进行，网格由AUTOGRID模块自动生成。为获得较高质量的计算网格，叶片通道采用4H-O 型结构化网格，叶顶间隙区采用蝶形网格拓扑结构(O 型网格内嵌有H 型网格)。通过网格相关性研究，并兼顾计算效率和求解精度，最终确定计算网格总数为158 万，其中近壁面网格高度为10-6m，网格最小正交性为14.3°。

数值计算通过FINE/Turbo 模块、用有限体积法求解圆柱坐标系下的三维定常Navier-Stokes 方程组。时间项、空间项分别采用4阶Runge-Kutta方法和中心差分格式进行离散，计算过程中CFL 数取3.0。紊流模型选择Spalart-Allmaras模型，级间参数传递选用守恒型交界面，同时采用隐式残差光顺及多重网格技术以加速收敛过程。

2.3 计算模型验证

为检验数值计算模型和计算方法的可信度，模拟计算了设计转速下两级风扇的气动性能，并与试验测量结果进行了对比，见图2、图3 所示。由于计算模型对部分结构细节进行了简化处理，使得计算流量较试验流量略偏大，计算效率较试验效率略偏低。但两者整体上具有较好的吻合性，可认为计算模型和计算方法具有良好的可信度。

图2 压比-流量特性Fig.2 Pressure ratio vs mass flow characteristics

图3 压比-效率特性Fig.3 Pressure ratio vs efficiency characteristics

3 计算结果分析

3.1 速度三角形分析

为更好地认识静子限位失效所诱发的转子、静子间及级间匹配失谐的影响机理，从典型速度三角形出发进行了相应的分析。图4给出了典型速度三角形分布(黑色实线为正常工况，红色虚线为静子限位失效工况)。当静子限位失效时，静子在气动力的作用下开始旋转，产生了一定的轮缘速度(us)，速度方向与其受力方向相同，即同转子叶片的旋转方向保持一致。静子叶片轮缘速度的存在一方面使得其自身的进口气流角向负攻角方向偏转，另一方面使得下游转子叶排的进口气流角同样向负攻角方向偏转，导致叶排的气流扭转角减小，加功量降低。总之，静子限位失效改变了上下游叶片排间的进口、出口气流角和加功能力的匹配，进而影响风扇/压气机部件的级间匹配参数及总性能。

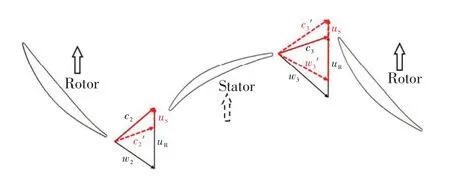
图4 速度三角形Fig.4 Velocity triangle

3.2 三维计算结果分析

3.2.1 周向限位失效对气动性能的影响

图5、图6 分别给出了第一级静子(S1)不同失效转速对应的风扇压比-流量和压比-效率特性分布。随着S1限位失效转速的逐渐提高，风扇部件的流量逐渐减小，温升效率逐渐提高。同时，最高状态点的压比逐渐降低，流量逐渐减小，即风扇的压比裕度降低，流量裕度增加。

图5 第一级静子限位失效时的压比-流量特性Fig.5 Pressure ratio-mass flow character with S1 displacement restrictor failure

图6 第一级静子限位失效时的压比-效率特性Fig.6 Pressure ratio-efficiency character with S1 displacement restrictor failure

图7～图9给出了S1限位失效时对应的级参数(转子总压比、转子效率、静子总压恢复系数)、90%叶高流场和90%叶高叶片表面静压分布。静子限位失效使得S1自身工作状态向大负攻角方向偏移(图9)，气动损失增加，静子的总压恢复系数降低(图7(c))。同时，前排静子的限位失效导致下游第二级转子(R2)的攻角偏负，气流转折角减小，加功量下降，总压比降低，进而加剧了下游通道的堵塞程度。受S1限位失效所引起的自身通道堵塞和R2 加功量下降所带来的下游通道堵塞两个因素的影响，上游第一级转子(R1)的出口背压提高，叶片通道内的槽道激波位置前移(图8 和图9)、激波损失降低，R1 转子效率提高。另一方面，R2进口攻角和马赫数的改变使得转子通道内激波结构出现明显变化，由初始的单波系结构逐渐变化为双波系结构，激波强度也随进口速度和马赫数的降低而逐渐降低，进而使得R2转子的效率也逐渐提高。

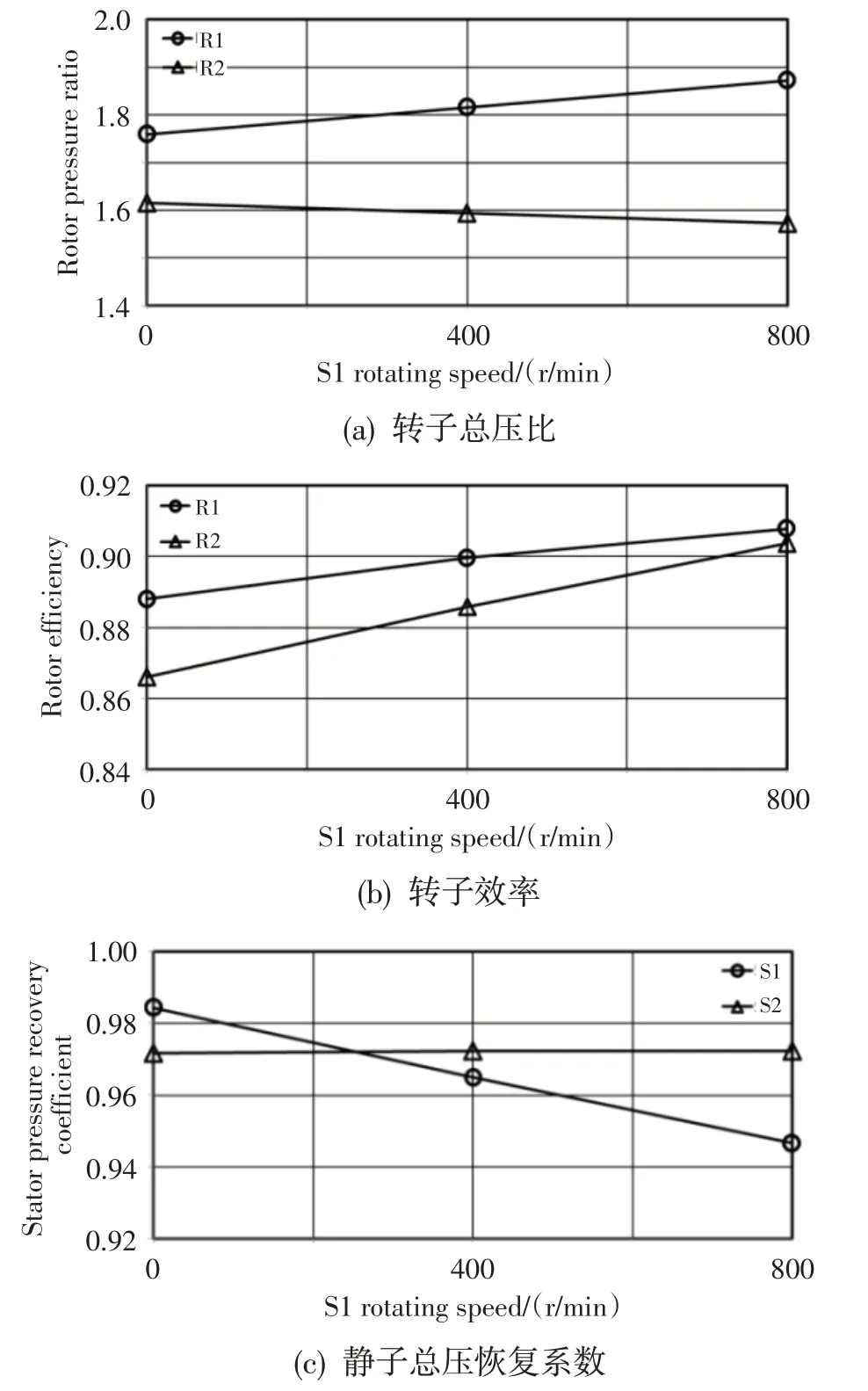
图7 第一级静子限位失效时对应的级参数分布Fig.7 The stage parameters with S1 displacement restrictor failure

图8 第一级静子限位失效时90%叶高的相对马赫数分布Fig.8 Relative Mach number at 90%span with S1 displacement restrictor failure

图9 第一级静子限位失效时90%叶高的叶片表面静压分布Fig.9 Static pressure distribution of blade surface at 90%span with S1 displacement restrictor failure

3.2.2 不同级限位失效影响特征分析

在多级压缩部件中，由于气动负荷和进出口边界条件的差异，不同级静子限位失效对自身工作状态及压缩部件整机气动性能的影响程度存在明显的差异。图10、图11分别给出了不同级限位失效对应的压比-流量和压比-效率特性分布。第二级静子(S2)限位失效较S1限位失效对风扇部件气动总性能的影响程度明显偏小，其对应的特性线与原始特性线近似重合，且随着静子限位失效转速的提高，其特性的变化趋势较小。但S2限位失效同S1限位失效表现出了相似的影响规律，即随着失效转速的提高，风扇部件的温升效率提高，压比裕度逐渐降低。

图10 不同级限位失效时的压比-流量特性Fig.10 Pressure ratio-mass flow character with displacement restrictor failure of different stages

图11 不同级限位失效时的压比-效率特性Fig.11 Pressure ratio-efficiency character with displacement restrictor failure of different stages

图12 给出了不同级限位失效时对应的级参数(转子总压比、转子效率、静子总压恢复系数)分布。受流场特征和上下游参数传递特性的限制，S2限位失效的影响仅局限于上游相邻的R2和自身，对上游不相邻的R1 和S1 的影响微乎其微，其对应的转子总压比、转子效率和静子总压恢复系数基本不变。S1 限位失效将影响上游相邻的R1 及下游的R2 和S2，且影响范围较S2 限位失效更为宽广。因此，S1限位失效对压缩部件气动性能的影响更明显。R2叶片通道内的槽道波明显削弱，无法有效影响上游的R1 和S1。因此，R1 叶排的激波结构和激波强度均未出现明显变化，总压比、效率等性能参数也保持不变。而S2限位失效，使得其自身的工作状态向负攻角状态偏移，对R2 产生一定的节流作用，导致R2 出口背压略微提高，激波位置前移，激波损失降低，效率提高。值得注意的是，无论是S1 限位失效还是S2限位失效，失效静子将面临较大的负攻角来流条件，使得静子的气动损失随着失效转速的提高而明显增大。

图12 不同级限位失效时对应的级参数分布Fig.12 The stage parameters with displacement restrictor failure of different stages

图13 不同级限位失效时90%叶高的相对马赫数分布Fig.13 Relative Mach number distribution at 90%span with displacement restrictor failure of different stages

4 结论

采用数值模拟方法研究了静子周向限位失效对压缩部件气动性能的影响机理，比较分析了不同级限位失效的影响程度，总结了相应的影响规律。主要研究结论如下：

(1)静子限位失效将导致静子产生一定的轮缘速度，对自身的进出口气流角、流通能力和损失特性带来影响，进而通过速度场和压力势的传播影响级内和级间的匹配状态，最终导致压缩部件整机的流量减小，压比裕度降低，温升效率提高。

(2)静子限位失效将改变压缩部件各级加功量的分配和流场特征的分布，导致级间原有的匹配失谐。其对上游转子存在一定的节流作用，使转子背压提高，激波位置前移，转子叶排的效率提高。同时，静子限位失效将导致下游转子叶排的攻角偏负，加功能力下降，进口马赫数降低，激波强度降低，效率提高。

(3)受上下游参数传递特征的限制，静子限位失效的影响仅局限于上游相邻的转子叶排和下游的转静子，无法对上游不相邻的叶排产生有效的影响，前排静子限位失效的影响程度较后排静子表现得更为明显。