过渡段横向刚度对悬臂动力涡轮模拟转子临界转速的影响

邓旺群，刘文魁，卢 波，唐虎标，冯 义

(1.中国航发湖南动力机械研究所，湖南株洲 412002；2.中国航空发动机集团航空发动机振动技术重点实验室，湖南株洲 412002)

1 引言

涡轴发动机动力涡轮转子主要有简支和悬臂两种结构形式。目前，国内外学者针对简支动力涡轮转子已开展了系统而深入的研究[1-8]，但针对悬臂结构动力涡轮转子的研究还非常有限[9-11]，有必要开展进一步的研究工作。

某涡轴发动机的燃气发生器转子和动力涡轮转子采用了轴承共腔设计，动力涡轮转子是一个超两阶弯曲临界转速的悬臂柔性转子，动力涡轮轴承座和机匣之间通过柔性过渡段连接。计算和试验均表明：转子的第二阶临界转速偏大，其相对于慢车转速的裕度不满足20%的设计准则要求，且进一步减小弹支刚度已很难实现。针对这一问题，设计了一个专供试验研究用的动力涡轮模拟转子。动力涡轮模拟转子与装机动力涡轮转子相比，除两级动力涡轮盘是模拟件外，其余均保持一致，并且两级模拟盘也是遵循与装机动力涡轮盘的质量和转动惯量基本一致的原则设计，这样可以确保在动力涡轮模拟转子上取得的研究成果能直接在装机动力涡轮转子上应用。

该动力涡轮模拟转子在前期的试验研究中，由于后转接段在额定工作转速范围内存在局部共振频率，导致转子挠度-转速曲线中出现三个共振峰值(前两个共振峰值分别对应转子的前两阶临界转速，第三个共振峰值由后转接段局部共振引起)，但通过后转接段及安装时涉及的后支座的改进设计解决了这一问题[9]。在此基础上，本文在高速旋转试验器上分别对带刚性过渡段和柔性过渡段的模拟转子进行了全转速范围内的临界转速试验，采用作者在文献[10]中提出的拟合插值方法得到了刚性过渡段的横向刚度，分析了过渡段横向刚度对模拟转子前两阶临界转速的影响，提出了通过改变柔性过渡段刚度适当调整转子临界转速的建议。

2 动力涡轮模拟转子

动力涡轮模拟转子的结构示意图见图1，主要由两级模拟盘、短轴、传动轴、测扭基准轴、轴承座等零部件组成，具有空心、薄壁、大长径比、内置测扭基准轴、两级动力涡轮模拟盘悬臂的结构特点；采用2-2-0的支承形式，1号和2号轴承采用喷射润滑，5号和6号轴承采用轴向环下润滑，1号和5号支承为刚性支承，2号和6号支承为带挤压油膜阻尼器的鼠笼弹性支承。

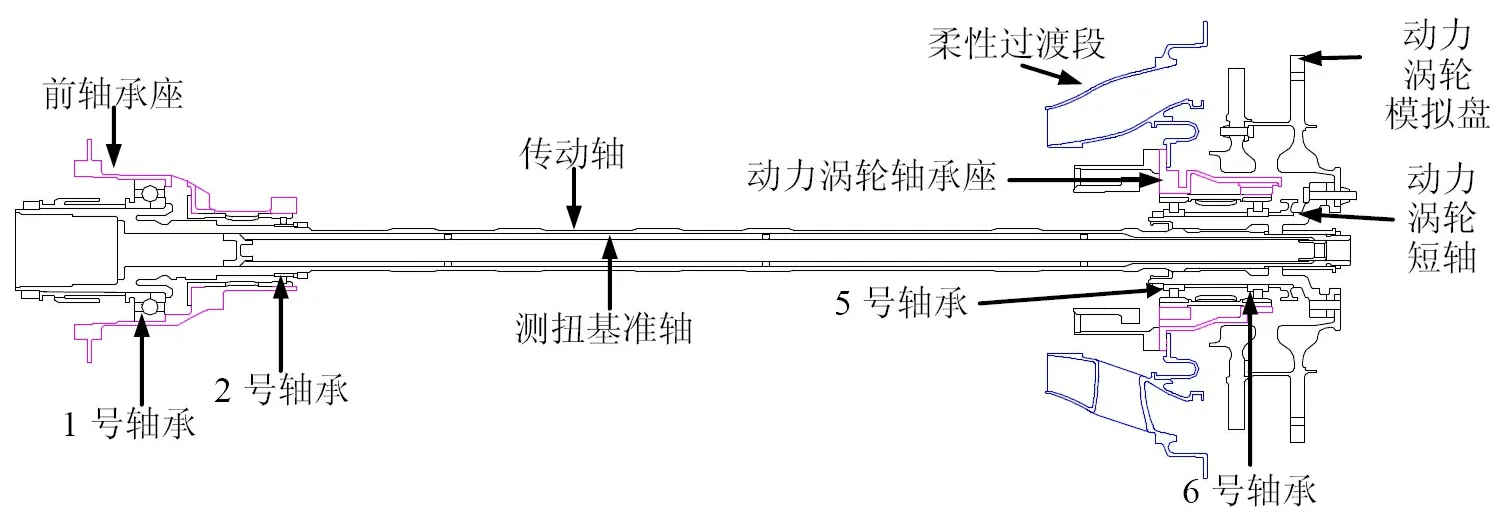
图1 动力涡轮模拟转子结构示意图Fig.1 Structure sketch of the power turbine simulated rotor

3 支承刚度及临界转速计算

根据文献[10]，在动力涡轮模拟转子计算模型中，2号和6号支承刚度均取对应弹性支承刚度的实测值，1 号和5 号支承刚度根据经验均取为5.000×107N/m，见表1；动力涡轮模拟转子前三阶临界转速的计算值见表2。

表1 动力涡轮模拟转子4个支承刚度值Table 1 The supporting stiffness of the power turbine simulated rotor

表2 动力涡轮模拟转子前三阶临界转速计算值Table 2 Calculation values of the first three critical speeds of the power turbine simulated rotor

4 动力涡轮模拟转子临界转速试验

4.1 试验设备

动力涡轮模拟转子临界转速试验在卧式高速旋转试验器上进行。该试验器由动力系统、传动系统、支承系统、润滑系统、真空系统和控制系统等组成，其转速和功率等均满足试验要求，滑油为8 号和20号滑油按一定比例的混合油。

4.2 带刚性过渡段的临界转速试验

试验过程中，通过如图2 所示的两端带花键的空心浮动轴，从动力涡轮模拟转子的输出端输入动力(与动力涡轮转子在发动机中的工作情况相反)驱动转子旋转。采用浮动轴连接可有效隔离试验器和转子之间的振动，并降低对中要求。在满足强度和传扭要求的前提下，空心结构可大幅减小浮动轴的质量。还使用了改进设计的后转接段，其在转子的全转速范围内均不会发生共振。改进设计前和改进设计后的后转接段的三维图见图3。

图2 浮动轴的三维图和二维图Fig.2 Graphic model and drawings of the floating shaft

图3 后转接段三维图Fig.3 Graphic model of the rear transfer section

带刚性过渡段动力涡轮模拟转子在临界转速试验中的安装及测试示意图见图4，图中⊥表示垂直方向，＝表示水平方向。刚性过渡段的三维图见图5，安装状态下刚性过渡段的实物照片见图6。

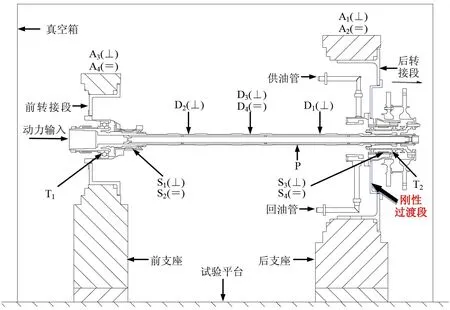
图4 带刚性过渡段动力涡轮模拟转子在临界转速试验中的安装及测试示意图Fig.4 Installation and measurement sketch during critical speed experiment of the power turbine simulated rotor with stiff transition section

图5 刚性过渡段三维图Fig.5 Graphic model of the stiff transition section

图6 安装状态下刚性过渡段的实物照片Fig.6 Photo of the stiff transition section under installation state

试验过程中，通过光电传感器P、电涡流位移传感器D1～D4、加速度传感器A1～A4、应变计S1～S4和热电偶T1～T2，分别测量转子转速(1个测点)、转子挠度(4 个测点分布在3 个测量面上)、支座振动加速度(2 个支座各2 个测点)、弹性支承应变(2 号和6 号弹性支承各2个测点)和轴承温度(1号和6号轴承外环各1个测点)。由于本文只关注临界转速，后续仅对D1～D4测得的转子挠度进行分析，其余测量参数均作为确保试验安全的监控参数。

由D1～D4位移传感器测得的转子挠度-转速曲线如图7 所示。图中，相对转速为各转速与额定工作转速之间的百分比，以下同。从图中可知：带刚性过渡段动力涡轮模拟转子在额定工作转速范围内存在两阶临界转速(对应两个共振峰值)，相应的临界转速值见表3。

图7 带刚性过渡段动力涡轮模拟转子的转子挠度-转速曲线Fig.7 Curves of rotor deflection versus speed of the power turbine simulated rotor with stiff transition section

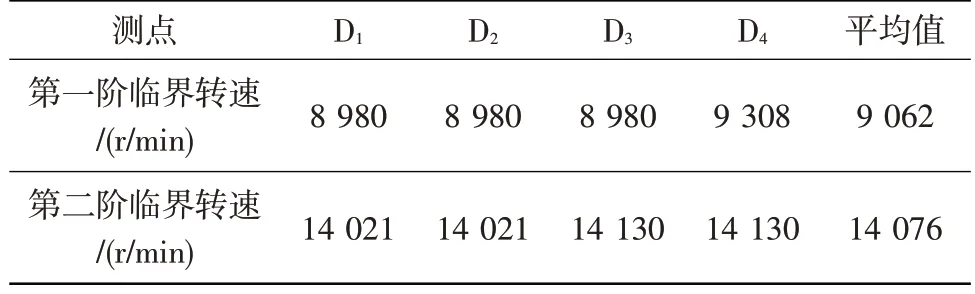
表3 带刚性过渡段动力涡轮模拟转子前两阶临界转速试验值Table 3 Experiment values of the first two critical speeds of the power turbine simulated rotor with stiff transition section

4.3 带柔性过渡段的临界转速试验

带柔性过渡段动力涡轮模拟转子的临界转速试验与带刚性过渡段动力涡轮模拟转子的临界转速试验，唯一的区别就是把刚性过渡段更换为了柔性过渡段，试验器、安装情况、测量参数、测试设备等完全一致。柔性过渡段的三维图见图8，安装状态下柔性过渡段的实物照片见图9。

图8 柔性过渡段三维图Fig.8 Graphic model of the flexible transition section

由D1～D4位移传感器测得的转子挠度-转速曲线见图10。从图中可知：带柔性过渡段动力涡轮模拟转子在额定工作转速范围内同样存在两阶临界转速(对应两个共振峰值)，相应的临界转速值见表4。

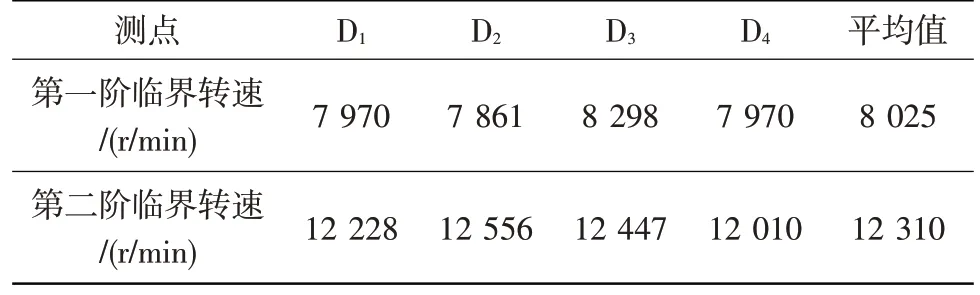
表4 带柔性过渡段动力涡轮模拟转子前两阶临界转速试验值Table 4 Experiment values of the first two critical speeds of the power turbine simulated rotor with flexible transition section

4.4 临界转速分析

根据表2～表4，可得到动力涡轮模拟转子分别装刚性和柔性过渡段时前两阶临界转速的计算误差(由式(1)计算)，见表5(表中的试验值均取平均值，以下同)。

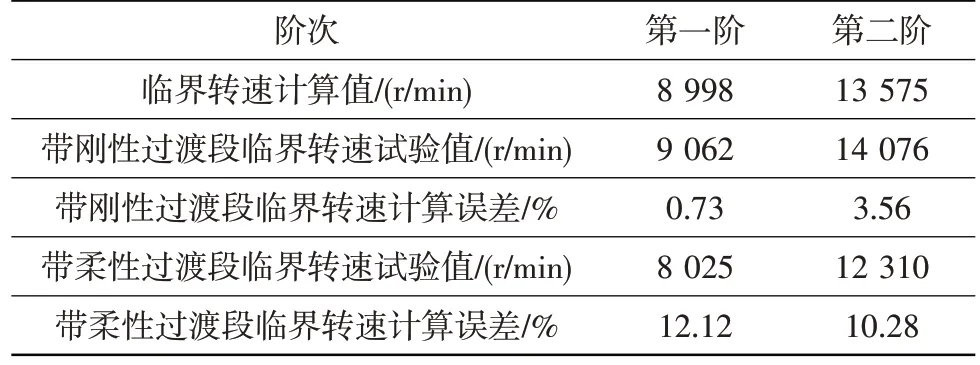
表5 动力涡轮模拟转子前两阶临界转速的计算误差Table 5 Calculation errors of the first two critical speeds of the power turbine simulated rotor

分析可得：①带刚性过渡段动力涡轮模拟转子前两阶临界转速的计算误差分别为0.73%和3.56%，误差较小，说明计算模型中各支承刚度的取值合适，无需根据临界转速试验结果对5号和6号支承刚度进行修正(原因见下文分析)。②带柔性过渡段动力涡轮模拟转子前两阶临界转速的计算误差分别达到了12.12%和10.28%，误差较大。显然，柔性过渡段明显降低了5号和6号支承刚度，需要根据试验结果对计算模型中5号和6号支承刚度的取值进行修正。

相比于文献[10]中使用改进设计前的后转接段和后支座的带柔性过渡段动力涡轮模拟转子的前两阶临界转速试验值(分别为7 971 r/min 和12 257 r/min)，本文使用改进设计的后转接段和后支座的前两阶临界转速试验值(分别为8 025 r/min 和12 310 r/min)仅分别变化了0.67%和0.43%。若考虑到测量误差等原因，前两阶临界转速的一致性非常好，说明转接段和后支座的改进设计不但消除了后转接段的局部共振问题，而且对前两阶临界转速也几乎没有影响。

5 刚性过渡段的横向刚度计算

文献[10]中，带柔性过渡段的动力涡轮模拟转子利用前两阶临界转速试验结果，采用拟合插值方法得到柔性过渡段的横向刚度K柔性过渡段=1.881×107N/m。同理，带刚性过渡段动力涡轮模拟转子利用前两阶临界转速试验结果，采用拟合插值方法可得到刚性过渡段的横向刚度K刚性过渡段，并同步得到5号和6 号支承的等效支承刚度K5等效和K6等效。具体步骤为：

(1)针对5 号和6 号支承，选取77 个组合支承刚度，运用SAMCEF 软件计算得到了带刚性过渡段动力涡轮模拟转子的第一阶和第二阶临界转速，见表6。表中，第1行为5号支承刚度，第1列为6号支承刚度，其余均为第一/第二阶临界转速；刚度的单位均为107N/m，临界转速的单位均为r/min。

(2)基于77 个组合支承刚度条件下第一阶和第二阶临界转速计算值，以及带刚性过渡段动力涡轮模拟转子前两阶临界转速试验值，利用仿真分析软件和spline样条函数插值法即可按下述步骤拟合出5号和6号支承的等效支承刚度。此时，第一阶和第二阶临界转速的计算值与其试验值相等。

①基于表6 中数据，在临界转速-5 号支承刚度-6号支承刚度三维坐标系中，拟合出带刚性过渡段动力涡轮模拟转子第一阶和第二阶临界转速的网格曲面，见图11。

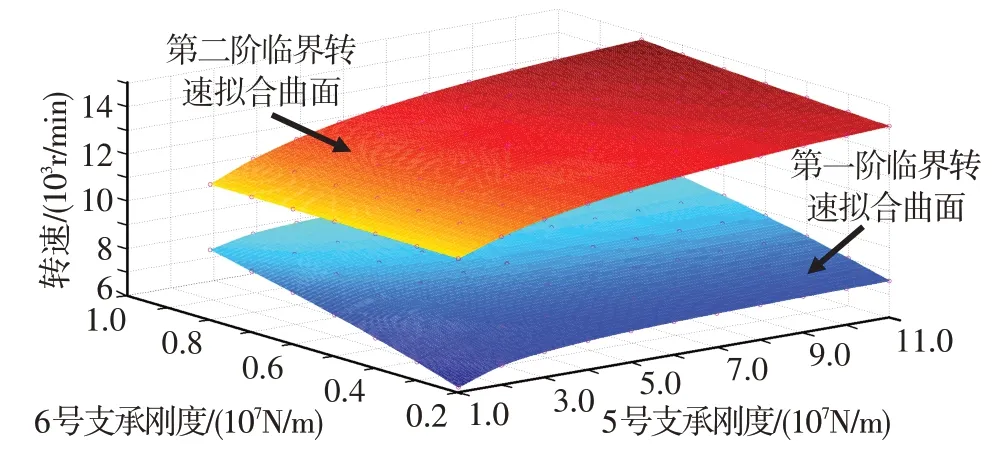
图11 拟合的第一阶和第二阶临界转速网格曲面Fig.11 Mesh surface of the fitted first and second critical speeds

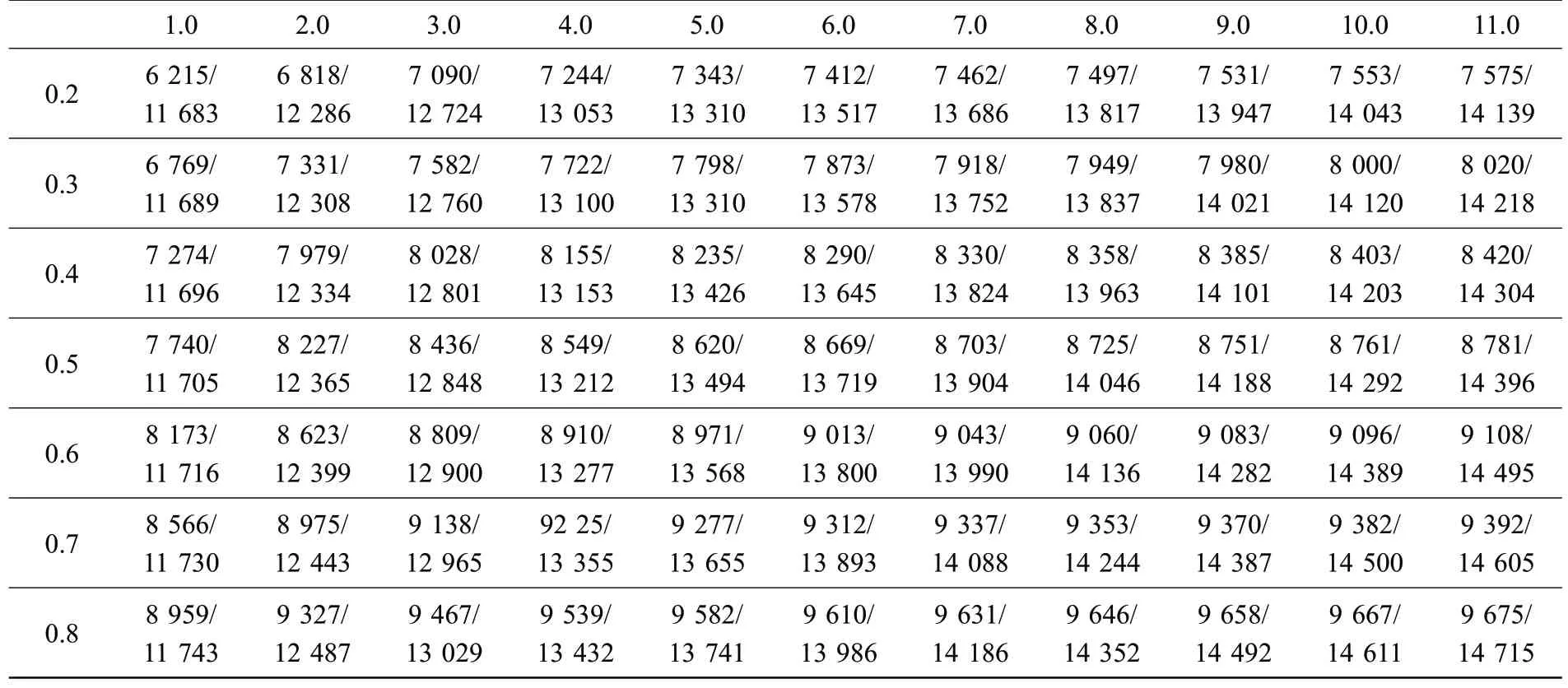
表6 带刚性过渡段动力涡轮模拟转子在77个组合支承刚度下的第一阶/第二阶临界转速计算值Table 6 The first/second critical speeds of the power turbine simulated rotor with 77 aggregate support stiffness

②在临界转速-5 号支承刚度-6 号支承刚度三维坐标系中，构造两个平面——这两个平面与两个支承刚度组成的坐标平面平行，转速坐标分别与第一阶临界转速ωcr1试验值9 062 r/min 和第二阶临界转速ωcr2试验值14 076 r/min 相等，见图12。两构造平面分别与两拟合网格曲面相交，得到两串空间离散交点。

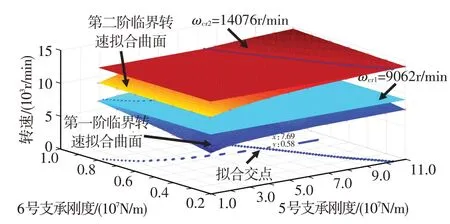
图12 第一阶和第二阶临界转速试验值构造平面与拟合网格曲面的交会示意图Fig.12 Intersection sketch between the plane of the first and second critical speeds test values and fitted mesh surface

③将两串空间离散交点投影到两个支承刚度组成的坐标平面内，然后用spline 样条函数对投影点进行插值，拟合出两条样条曲线，两条样条曲线的交点坐标即为5 号和6 号支承的等效支承刚度，即有K5等效=7.690×107N/m，K6等效=0.580×107N/m。

假设6 号轴承、鼠笼弹性支承和动力涡轮轴承座的横向刚度串联值为K6，由于6 号轴承和动力涡轮轴承座的横向刚度值均远大于鼠笼弹性支承的刚度值，因此K6可直接取为6 号鼠笼弹性支承的刚度值，即K6=0.608×107N/m。

刚性过渡段和K6同样是串联关系，有：

据此，即可得到K刚性过渡段=1.259×108N/m。

6 支承刚度合理性分析

K5等效和K6等效是根据临界转速试验结果并采用拟合插值方法得到的实际刚度，其与计算模型中5 号和6号支承刚度取值(表2)的对比见表7。表中变化率按式(3)计算。

表7 5号和6号等效支承刚度与计算模型中支承刚度的对比Table 7 Comparison between the equivalent support stiffness and support stiffness of calculation model of the number 5 and number 6 support

对计算模型中5 号和6 号支承刚度取值的合理性进行分析：

(1)5号支承的等效支承刚度比计算模型中支承刚度增大了34.98%。根据文献[10]中动力涡轮模拟转子前两阶临界转速随4个支承刚度的变化规律曲线可知，只要5号支承刚度大于4.7×107N/m，前两阶临界转速几乎不再随5 号支承刚度的变化而变化。显然，5 号支承刚度无论是在计算模型中的取值还是采用拟合插值法得到的等效刚度均满足这一条件，因此尽管5 号支承的等效支承刚度比计算模型中取值增大了34.98%，但计算模型中5 号支承刚度的取值对前两阶临界转速的计算结果不会有实质性的影响。

(2)6号支承的等效支承刚度仅比计算模型中支承刚度减小了4.83%。事实上，6 号支承刚度为6号轴承、鼠笼弹性支承、动力涡轮轴承座和过渡段四者刚度的串联，并且K刚性过渡段高达1.259×108N/m，6号轴承和动力涡轮轴承座的横向刚度也均在108N/m级。因此，只要过渡段是刚性的，6号支承的等效支承刚度就基本上由6号弹性支承刚度(106N/m级)决定，这样计算模型中6 号支承刚度的取值对前两阶临界转速的计算结果也不会有实质性的影响。

根据上述分析：在装刚性过渡段条件下，从前两阶临界转速计算结果的正确性来说，计算模型中5号和6 号支承刚度的取值均是合理的。此外，根据文献[10]，计算模型中1 号和2 号支承刚度无需修正。因此，计算模型中4 个支承刚度的取值均是合理的，这就是带刚性过渡段动力涡轮模拟转子前两阶临界转速的计算误差分别仅为0.73%和3.56%的原因。

7 基于过渡段横向刚度的临界转速调整措施

过渡段从柔性变为刚性，动力涡轮模拟转子前两阶临界转速试验值有明显变化。前两阶临界转速随过渡段横向刚度的变化关系见表8。表中，支承刚度变化率、临界转速变化率分别按式(4)和式(5)计算。

表8 前两阶临界转速随过渡段横向刚度的变化关系Table 8 Variation relationship of the first two critical speeds with the crosswise stiffness of transition section

从表8可知：过渡段从柔性变为刚性，其横向刚度增大了85.06%，动力涡轮模拟转子的前两阶临界转速分别相应增大了12.92%和14.35%。基于动力涡轮转子和动力涡轮模拟转子的良好一致性，显然动力涡轮转子也具有同样的规律，这对于调整装机动力涡轮转子前两阶临界转速具有重要的工程意义。如装机动力涡轮转子第二阶临界转速相对于慢车转速的裕度(计算公式见式(6))小于20%的设计准则要求，且继续降低6 号弹性支承刚度已非常困难(如继续降低刚度，鼠笼弹条将变得很细，不但加工困难，而且强度也不能保证)，即通过降低弹性支承刚度来降低第二阶临界转速已很难实现，这时可以考虑在保证强度的前提下适当降低柔性过渡段的横向刚度。

经分析，假设动力涡轮转子第二阶临界转速相对于慢车转速的裕度需从15%提高到20%，此时第二阶临界转速需降低约5.88%，在不采取其他措施的前提下，只需把柔性过渡段的横向刚度降低约35%即可满足要求。

8 结论

针对过渡段横向刚度对某涡轴发动机悬臂动力涡轮模拟转子前两阶临界转速的影响开展了研究，主要结论如下：

(1)过渡段的横向刚性对动力涡轮模拟转子的前两阶临界转速有明显影响，可以通过改变过渡段的横向刚度适当调整前两阶临界转速。过渡段的横向刚度增大85.06%(从柔性到刚性)，转子的前两阶临界转速分别增大12.92%和14.35%。

(2)过渡段为柔性过渡段时，必须根据临界转速试验值采用拟合插值方法等对计算模型中5号和6 号支承刚度的取值进行修正；过渡段为刚性过渡段时，不需要根据临界转速试验值对计算模型中5号和6 号支承刚度的取值进行修正，即计算模型中支承刚度的取值不会影响前两阶临界转速计算结果的正确性。

(3)对于带柔性静子连接件的高速转子，若不能通过采取其他措施(如改变弹性支承刚度等)来调整临界转速，在保证强度的前提下，可以通过改变柔性连接件的横向刚度适当调整转子系统的临界转速。